Modelling applications in trends of environmental sciences are currently very much sought after in identifying the determinants affecting the ecosystem. This study thus aspires to demonstrate the modelling procedures in the study of the relationship between the concentration of heavy metals in the soft tissues and the physical properties of Geloina similis by using the exponential regression modelling approach. Data collected for this study were obtained from a mangrove lagoon in Salut, in the state of Sabah, East Malaysia. Experimental analyses were carried out in the laboratory of the Environmental Science Program of the Faculty of Science and Natural Resources, Universiti Malaysia Sabah. Physical properties of molusc (Geloina similis) considered were differences in length, height, width, wet weight, and dry weight, besides the length and width of the soft tissues. Mathematical modelling procedures were then employed, involving listing out all the possible models, model transformation of non-linear to linear models, multicollinearity test, coefficient test, followed by the Runs test and residuals normality test. The best model obtained was tested for its robustness and accuracy for prediction via the Mean Absolute Percentage Error (MAPE). Findings showed that the physical properties of Geloina similis involving height (X₂), wet weight (X₄), and interaction between height and length tissue (X₂A), had significantly contributed to the concentration of heavy metals accumulation (HMA) as given by equation:. Due to the absorption habit of Geloina similis, and the presence of heavy metals in the soils, it can be concluded that the presence of heavy metals concentration in the soft tissues of G.similis are thus found to have significant relationship with the molusc physical properties.

Keywords: environmental sciences, physical properties, heavy metal accumulation, model transformation, exponential models

MAPE, mean absolute percentage error; HMA, heavy metals accumulation; Pb, lead; Cu, Copper; Cr, Chromium; Cd, Cadmium; Zn, Zinc; GOF, goodness-of-fit; DV’s, dependent variables; VIF, variance inflation factor; 8SC, eight selection criteria; IV’s, independent variables; WT, width tissue; LT, length tissue; WWt, wet weight; DWt, dry weight

Mangrove forests are one of the nurseries for some of the marine creatures especially the bivalve molluscs in the sediment area. Mangrove forests bring about the ecosystem by providing habitat for a few species of mud clam. Mangrove ecosystems re-evaluated as the important intertidal wetland, which only can be found in tropical or sub-tropical areas.¹ The ecosystems provide a diversity of ecological benefits including not only being highly productive, but also performing as nursery and a haven region for biodiversity. In addition, mangrove forests are capable to function as a protection against coastline erosion. Mangroves have roots that functions to trap soft sediments. Significantly, these sediment-trapping root systems not only act as a cushion for the coastal area against wave-induced erosion, but also capable of protecting the coastal ecosystems from the erosion of the shoreline.² Geloina similis are a kind of rare mud clam that can be found in the mangrove swamps area especially in the bottom of sediment. Recently, the mud clam is severely contaminated by heavy metals due to the intense industrialization which contributes to the high concentration of heavy metals in the sediment area. G.similis stores these contaminants in their soft tissues.³

Long-term pollution caused by human activities had led to high contamination of heavy metals that had been recorded in mangrove sediments all over the world.^4,5 Heavy metal is considered as one of the most impacted pollutants in this natural environment because of their toxicity, persistence and bioaccumulation problem, besides being non-biodegradable, and persistent in the environment.⁶ Therefore, sediments that contained high concentrations of metals once they were ingested by the suspended filter-feeder become bio-available as sources of metal uptake by the mussels.⁷ Besides, mangrove forests have an important role in the biogeochemistry of trace metal contaminants in coastal areas. They buffer and immobilize heavy metals before reaching nearby aquatic ecosystems.⁸ The mangroves polluted by the heavy metals are associated with anthropogenic inputs such as industrial effluents, agro-based industries, agricultural runoffs, sewage treatment plants, leaching from domestic garbage dumps, urbanization, and chemical and oil spills.⁹ The heaviest metals, such as copper, lead, and zinc, were accumulated in aquatic organism were then consumed by humans. Thus, the presence of heavy metals has received significant attention due to their long-term effects on the environment, especially in the coastal regions. While there exists various types of Heavy Metals Accumulation (HMA), the concentrations of heavy metals in this paper are focused on lead (Pb), Copper (Cu), Chromium (Cr), Cadmium (Cd), and Zinc (Zn). There is some study resources related to G.similis and other Geloina as well. However, there is no availability of previous research on bivalve mollusc (Geloina similis) using a mathematical model. While other works had been referred to as contribution in a linear relationship, this study expounds further to determine the nonlinear relationship between the different amounts of heavy metals concentration accumulated in the soft tissues, and as relative to the physical properties of Geloina similis using exponential modelling procedures.

Study site

This study had collected ninety samples of G.similis from the Salut area of mangrove forests in Sabah as shown in Figure 1¹⁰ of latitude 6˚6’4.18”N and longitude 116˚10’22.78”E . Data had included the physical properties of G.similis samples, namely, the height, and width of the molusc shells, wet weight and dry weight of the total soft tissue of the sample, and the accumulation of each heavy metal concentration (Zn, Pb, Cu, Cr, and Cd) carried out during the experimental laboratory analyses.

Figure 1 Study site at Salut Mangrove Forests, Sabah.¹⁰

Mathematical modelling

Exponential model is frequently used in solving problems related to changes in populations, pollution, temperature, bank savings, drugs in the bloodstream and radioactive materials, so as to name a few. An exponential function is classified when it has a base that is constant and an exponent that is a variable. The general function of the exponential model is shown in Equation (1) below:

General Exponential Model Equation: $P_i=a_i{e}^{b_i(X_i)},b_i>0$  (1)

Where P=dependent variable, X=independent variable, a=constant variable, b=constant variable, and e=base of the function, with i=1, …, n with ‘n’ is the number of dependant variables. The value of the constant variable, ‘b’ should be more than zero for the function to be valid. This is due to the fact that it is not possible to determine the value of the dependent variable, ‘P’ as the value cannot be calculated. Although the exponential function and the logarithmic function seem the same in the function, but in fact, they are not. The inverses of the exponential function are regarded as the logarithmic function. The function for logarithmic function is shown below in Equation (2):

Logarithmic Function:$Y_i=Ln{p}_i=a_i{b}_i{}^{c_i(X_i)}=\ln a_i+c_i\ln b_i(X_i)={\beta }_0+{\beta }_i{X}_i$  (2)

Where b= base of the function, a= constant variable, c= constant variable, X= independent variable, for i=1, 2,…, n with n is the number of dependent variables.

Before the exponential regression equation is applied on any case of study, basic assumptions are important to be identified. This is done to check whether the equation is appropriate to the case, and hence satisfies these assumptions. Three assumptions that are needed to be considered are:

1. Continuous reproduction;

1. without seasonality consideration for continuous reproduction;

2. All organisms are identical;

2. The organism under study is Geloina similis;

3. Constant environment with respect to space and time;

3. The habitat is unaffected by changes from the surroundings. 

Data analyses

Figure 2 depicts the modelling flowchart showing all the procedures involved in this research, starting with experimental data comprised of site data collection and laboratory analysis, mathematical variables identification, factor analysis and dummy transformation, treating outliers, data partitioning for modelling (90%) and forecasting (10%). Preparing the data facilitates statistical analysis, and this includes checking for data normality, identifying necessary extracted variables, statistically adjusting for outliers and data transformation.¹¹ Non-normal data were transformed into normality by using basic transformation such as logarithmic function and square root transformation.¹²

Figure 2 Modelling Flowchart.

Exponential model obtained will then undergo normality and randomness tests for its goodness-of-fit (GOF), and finally, the transformed data are substituted back into the exponential regression equation for interpretation. Procedural summary of the modelling flowchart are as shown in Figure 2 below.

Dummy variables were identified by carrying out Factor Analysis in SPSS version 22. It is used to select the factors by extraction so as to identify the importance of the variables chosen. Theory is the first criteria to determine the number of factors to be extracted. From theory, the number of factors extracted does have to make sense. Criteria for practical and statistical significance of factor loadings can be classified based on their magnitude such as follows:

1. Greater than 0.30 — minimum consideration level;
2. Greater than 0.40 — more important;
3. Greater than 0.50 — practically significant.

Variables with significance lower than 0.50 will be chosen as dummy variables. In this study, the practice of dichotomization on quantitative measures will be based on the median value which was known as median split.¹³ An observation that appears to deviate markedly from other observations in the sample is called an outlier.¹⁴ Outliers were observed using boxplots and extreme values table computed to check for the presence of extreme values or outliers. Winsorization is a common way in dealing with outliers. It is the statistical transformation by restricting extreme values to reduce the influence of possibly spurious outliers in the statistical data. It is the modification of one or more data points at the end of the tails of the distribution to the next highest or lowest values within the distribution that are not suspected to be outliers. Instead of truncating or trimming the outliers, simply just modify the outliers to the next lowest or highest value in the tail of each side of the distribution. Winsorization is used because the valid data points were derived from a heavy-tailed distribution. Without dealing with outliers, it might affect our statistical analyses. Winsorizing data points were highly considered because the outliers probably might greatly affect the accuracy of the significant p-value, that is, it becomes more consequential to the p-values in terms of accuracy.

Data distribution

The data collected had thus undergone experimental laboratory analyses based on the five heavy metals accumulated in the soft tissues. The data set for each metal was then categorized into two partitions which were 90% for partition P1 (for modelling), and 10% for partition P2 (for prediction):

1. Partition P1: Modelling;

1. 90% of observations were used in modelling purpose in the attempt to obtain the best model in this research. It accounts for 81 samples for the data sets;

2. Partition P2: Verification by Mean Absolute Error Percentage (MAPE);

2. In this partition P2, 10% of data was accounted for forecasting purpose. Nine samples were chosen randomly for each data set.

Descriptive statistics were used to describe the basic features of the data by providing simple summaries about the sample and measures; with simple graphic analysis.¹⁵ Quantitative descriptions were also presented in a manageable form.¹⁶ The model-building procedures can be referred to as in^17,18 and the Four Phases.¹⁹

The phases of model-building approach in Figure 3 can be described simplistically as follows:- 

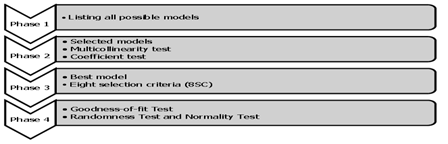
Figure 3 The Four Phases in Model Building Procedures.¹⁹

Phase 1 - all possible models: In the development of the Exponential models for these datasets, the concentration of heavy metals accumulated in the soft tissues would be the Dependent Variables (DV’s) noted by P_i, where i=1,2,…..,5 based on the five heavy metals tested; whereas, length (X₁), height (X₂), Width (X₃), dry weight (X₄), and wet weight (X₅) would be the Independent Variables (IV’s). Length tissue (A) and width tissue (B) were included as independent dummy variables in the models. Dummy variables were executed during the calculation of the possible models but included in the models before model-building procedures were carried out. The number of all possible exponential models, N can be calculated by using the formula:

$N={\displaystyle \sum _{j=1}^{q}j({}^{q}C{}_j)}$  (3)

Where, ‘N’ is the number of all possible models generated, and ‘q’ is the number of variables, and j=1, 2,…, q. 

Phase 2 - selected models: After running the models using the SPSS, there were a few selected models obtained. The selected model was first determined using the Multicollinearity Test via the VIF values obtained. Multicollinearity test can be carried out in two ways which are by testing the correlation based value or through Variance Inflation Factor (VIF). In this study, VIF value used will be 5. The overall procedure to remove the variables via multicollinearity by using VIF is shown in Figure 4. This can be done in SPSS by going to Analyzeà Regression à Linear à Enter the required variables. The variable(s) with VIF>5.0, would be eliminated first. Subsequent elimination was carried out until the variables left were of VIF values less than 5.0.¹⁸ After the Multicollinearity Test, the next step was to conduct the Coefficient Test. Coefficient test was done by eliminating sequentially one at a time the variable(s) that had p-values more than 0.05.

Figure 4 VIF Test Procedures of Multicollinearity Removals.^20,21

The coefficient test was also applied to test the coefficients of the corresponding variables. The variable with a condition that the highest p-value and greater than α=0.05 would be removed where an example of model labelling is given as: let say M19 as the ‘parent’ model with 5 multicollinearity variables removed, and 2 insignificant variables eliminated from the coefficient test .²¹ 

Phase 3 - best model: In order to achieve the best model, Eight Selection Criteria (8SC) as in Table 1 were also used in this paper.¹⁷

Phase 4 - goodness-of-fit: Lastly, goodness-of-fit (GOF) test was also used to ensure how well the model fits into the problem or data based on the standardized of residuals. To determine the randomness of the residuals, a randomness test is done to determine them. If the value obtained is larger than 0.05, thus the null hypothesis is accepted and vice versa.

The Mean Absolute Percentage Error (MAPE) is used to check the accuracy of the model as it produces a measure of relative overall fit.³⁰ The purpose of MAPE is to verify the reliability of the best model which was obtained in the phase three. MAPE measures the error size of the model and usually expresses accuracy as a percentage.³¹ MAPE is defined by the formula as shown in (4):

$MAPE=\frac{1}{m}{\displaystyle \sum _{t=1}^m\left|\frac{A_t-F_t}{A_t}\right|}x100\%$  (4)

Where, 𝑚= sample size of reserved data, 𝐴_𝑡= actual value of dependent variable given, and 𝐹_𝑡= estimated value of dependent obtained. The interpretation of different values of MAPE is shown in Table 2.

The best model is accepted if the percentage value of MAPE is from below 10% up to 15%. However, the model is still acceptable if the value of MAPE is less than 25%. A lower MAPE value would indicate that the best model can be used in forecasting or prediction. Otherwise, the best model would be rejected.

Variables identification

In this study, the heavy metals concentrations of Zinc, Lead, Copper, Cromium and Cadmium respectively given by their atomic symbols (Zn, Pb, Cu, Cr, and Cd) in total soft tissue of G.similis were used as dependent variables (DV’s). Meanwhile, there were seven independent variables (IV’s) in terms of physical factors studied as shown in Table 3. The data were identified with the symbol given below to ease in the data preparation procedures. The symbols were labelled before relevant transformations were performed.

Factor analysis

Table 4 showed the results of the factor analysis that was carried out to identify the dummy variables. It could be seen that five independent variables which were length, height, width, wet weight and dry weight were more important since they showed higher number of possible causes greater than 0.5. Meanwhile, width tissue and length tissue variables (highlighted yelow in Table 4) were of lesser importance with lower number of possible causes that were lower than 0.5. Hence, these variables were chosen as dummy variables and then were converted into categorical variables in this study.

Dummy transformation

With 90 observations considered, the median values for the dummy variables (width tissue and length tissue) were computed from SPSS as shown in Table 5. Dummy code 0 will be assigned to observations below the median values of 3.800 and 4.050 for width tissue (WT) and length tissue (LT) respectively, while code 1 is assigned to values greater than the median values. These dummy codes are interpretated as value 0 for small size of G.similis, and value 1 for big size of G.similis. The width tissue variable will be then labelled as A, while the length tissue variable is labelled as B in the regression equations.

Checking and treating outliers

Figure 5 and Figure 6 below depicted the presence of outliers of the physical properties of G.similis and concentrations of heavy metals in the soft tissues respectively. It can be seen that wet weight and dry weight of the physical properties both have outliers in the boxplot graphs, while other physical properties do not have any outliers. Meanwhile, variables in Figure 6 were arranged accordingly to the concentration of heavy metals: Zinc (Zn), Copper (Cu), Lead (Pb), Cadmium (Cd) and Chromium (Cr).

Figure 5 Boxplot graphs of physical properties of G.similis.

Figure 6 Boxplot graphs of heavy metal concentrations of G.similis.

Outliers are needed to be treated and not removed so as to improve data robustness for modelling. Table 6 showed that there was only one outlier found in Wet Weight (WWt), precisely in case number 71 with value of 28.16380. However, extreme values and outliers were highly detected too in the Dry Weight (DWt) variable. Table 7 showed details of the extreme values and outliers of the heavy metal concentrations taking regard about the case numbers from the 90 observations as well as the values of observed data. A total of six extreme values and eight outliers were detected so these have to be treated for robust estimation and prediction.

Outliers detected were treated by standard statistical procedure called winsorization. Winsorization procedures were proposed to replace extreme values with less extreme values, effectively moving the original extreme values toward the centre of the distribution (Table 8).³²

For independent variable, wet weight WWt with only one outlier was determined, the outlier with value 28.16380 will be modified into 26.47730 which is the next highest value within the distribution. 26.47730 were originated from the case number 63 out of the other observed values. On the other hand, the extreme values and outliers for variable dry weight; DW will be modified into value 2.43, the highest value from case number 64 which was within the distribution. After treating outlier for independent variable, outliers and extreme values for each dependent variable were also replaced with the values as in the Table 9 below:

Descriptive statistics

For concentration of heavy metals, the summaries showed all the variables were positively skewed with higher mean value compared to the median as well. All the kurtosis values lie within the range of the rule of thumb proposed. This indicated that no measurement of extremity tails of the distribution. Only variables Zn and Cu showed approximately symmetric distribution with skewness value 0.4420 and 0.4050 respectively. Further tests will be conducted with graphs to prove the distribution of each variable. Table 10 depicts the descriptive statistics of the heavy metal concentrations in this study while Table 11 indicated the variables, types and symbols used for further modelling.

For this study, q=5 (excluded the 2 dummy variables), the number of all possible models would be: $N=1({}^{5}C{}_1)+2({}^{5}C{}_2)+3({}^{5}C{}_3)+4({}^{5}C{}_4)+5({}^{5}C{}_5)=80$ , as shown in Table 12 below. The transformation of non-linear to linear model equations was partially shown below. From Equation (1), non-linear exponential equation can be given as: $P_i=a_i{e}^{b_i(X_i)},b_i>0$ . From equation (2), the transformed equation is in the form of $Lnp=\ln \alpha +({\beta }_1{X}_1+{\beta }_{A}A+{\beta }_{B}B+\mu )$ . Assume that, 𝑌=ln𝑃, and 𝛽₀=ln𝛼, then, the equation will be in the form: $Y={\beta }_0+{\beta }_1{X}_1+{\beta }_{A}A+{\beta }_{B}B+\mu$ . The 80 transformed model equations are applied to each of the five data sets of dependent variables on the heavy metals, thus amounting to 400 possible exponential model equations obtained.

Model building procedures of Phase 1 to Phase 4 were carried out on the regression equations. Table 13 below showed the summary of the selected models of Phase 2 on heavy metal Zn denoted by Data set 1.

Table 14 showed the values of the eight selection criteria of Phase 4 of the model building procedures. It can be seen that model M48.9.2 shows the lowest value among all the other models on Zinc. Therefore, it can be concluded that the model M48.9.2 is the best model with respect to the heavy metal (Zinc) concentration. The selected general equation of M48.9.2 is given as: ${\stackrel{⌢}{Y}}_1={\beta }_0+{\beta }_2{X}_2+{\beta }_4{X}_4+{\beta }_{12}{X}_{12}$ . Similar procedures were carried for all the other dependent variables of Lead, Copper, Cadmium and Chromium respectively. Table 15 listed the best model equations of all the heavy metal concentrations, except for Lead which had all its model equations being removed due to high multicollinearity and insignificant variables.

Table 16 above shows the goodness-of-fit tests, namely the Runs test and normality test for Zn. Since the value of the asymptote significant is 0.105 which is >0.05, then the null hypothesis is not rejected. In other words, the standardized residual, u_i are randomly distributed. Since the sample size is more than 50, normality test based on Kolmorov-Smirnov shows a p-value of more than 0.05. This also indicates that the residuals are normality distributed.

Exponential Smoothing was conducted to examine the accuracy of the model. Exponential smoothing technique is one of the most important quantitative techniques in forecasting. The accuracy of forecasting of this technique depends on exponential smoothing constant. Choosing an appropriate value of exponential smoothing constant is very crucial to minimize the error in forecasting.

For illustration purposes, Table 17 showed the actual value and the calculated forecasted value for Zinc. The values were then substituted in the equation so as to calculate MAPE as shown below.

$\begin{array}{c}MAP{E}_{Zn}=\frac{1}{m}{\displaystyle \sum _{t=1}^m\left|\frac{A_t-F_t}{A_t}\right|}x100\%=\frac{1}{9}(0.3089999969)x100\%\\ =3.43\%\end{array}$

Similarly, MAPE for the other heavy metals, namely for Cu(Y₂) , Cd(Y₄) and Cr(Y₅) were calculated, and were given as Cu: 44.3%, Cd: 19.98%, and Cr: 9.32% respectively. It can be seen that exponential model from Zinc is the best to be used for forecasting the heavy metal concentration accumulation of G.similis.

The best models are obtained by calculating the 8SC based on each data set of heavy metal concentration, namely, Zinc, Copper, Cadmium, and Chromium, except for Lead, since all the variables are highly correlated and insignificant. Based on the results obtained in Table 15, the best models for the heavy metals (Zn, Cu, Cd, Cr) produced an exponential curve which is almost linear. The physical properties which affect the concentration of accumulation are height (X₂), width (X₃), wet weight (X₄), dry weight (X₅), and length tissue (A), except for length (X₁), and width tissue (B). The best model for heavy metal Zinc concentration accumulation is M48.9.2. The reduced model equation of the best model is shown as below: M48.9.2: ${\stackrel{⌢}{Y}}_1=ae{\beta }_2{X}_2+{\beta }_4{X}_4+{\beta }_{2A}{X}_{2}A$ . The best model can be written in the form of estimated model with the coefficient value as shown as: ${\widehat{Y}}_1=0.787+0.587X_2+0.363X_4-0.159X_{2}A$ , where, ${\widehat{Y}}_1$ = concentration of heavy metal Zinc; 𝑋₂= height; 𝑋₄=wet weight and 𝑋₂𝐴= interaction between height and length tissue. By log transformed, the exponential equation is thus given by $P_{Zn}=0.787e^{0.587X_2+0.363X_4-0.159X_{2}A}$ . The model has two single independent variables and one first order interaction. The positive coefficient values show that the concentration of heavy metal Zinc would increase if the corresponding variables, 𝑋₂ and 𝑋₄ increase. Model equation also shows that Zinc concentration is positively affected by the increment in the zero interaction of height, 𝑋₂ and the wet weight, 𝑋₄ of G.similis, and is negatively affected by the first order interaction between height (𝑋₂) and length tissue (A) . This thus indicated that these two variables, height and wet weight, are the main single contributors to the concentration of Zinc accumulation in the soft tissue of G.similis. The concentration of Zinc showed a positive value as the constant was positive, no matter of any increment for the height and wet weight. This was because the model showed a positive intercept which was 0.787. For every additional of one unit in height, 𝑋₂ will directly increase the concentration of Zinc by 0.587 and for every additional of one unit in wet weight, 𝑋₄ will directly increase the concentration of Zinc by 0.363. This also shows that 𝑋₂ is more dominant than 𝑋₄.

Active feeding behaviour possessed by the mollusc may raise the concentration of heavy metals in its tissue.³³ Mollusc is also exposed to different food suspensions consisting mixtures of sediment, particulate matter. The different concentrations of pollutants may affect the growth of mollusc in aquatic environment as well. There are a lot of factors that can affect the concentration of Geloina in real-world phenomena. It is recommended that the study of heavy metals concentration shall not just be based on the physical properties. Hence, further works on these aquatic environmental factors in this study site and other similar sites such as this, are recommended.³⁴

This study had identified the relationship between the concentration of heavy metals accumulation and the physical properties of Geloina Similis via exponential regression models. Exponential regression modelling techniques are exemplified as well as illustrated. Modelling procedures cum statistical tests are employed, and have proven to obtain a robust model for prediction and forecasting. This study had identified the variables that are affected by the concentration of heavy metals accumulation on G.similis via the nonlinear exponential regression. The relationships between the concentration of heavy metals and the G.similis physical properties have all involved the height, width, wet weight, dry weight and length of soft tissue, particularly Zinc, where height and wet weight are significant contributors. The validity of the model has been tested based on the goodness-of fit test, and the accuracy and reliability of the model is obtained via MAPE (3.43%), which thus indicates that the exponential model is a very good model for estimation and prediction. All these statistical tests and analyses had thus indicated that modelling using exponential regression models gives robustness and are excellent in giving good estimates in prediction.

The authors would like to thank Universiti Malaysia Sabah for providing the fund for this research under the grant number SGK0009-STWN-2015. Our thankful appreciation to Ms. Lau Wei Eng for helping out partially in the statistical analyses performed during modelling.

None.

Authors declare no conflict of interest exists.

1. Pumijumnong N, Danpradit S. Heavy Metal Accumulation in Sediments and Mangrove Forest Stems from Surat Thani Provice, Thailand. The Malaysian Forester. 2016;79:212–228.
2. Spalding M, Mclvor A, Tonneijck FH, et al. Mangroves for coastal defence. Guidelines for coastal managers & policy makers. Wetlands International and the Nature Conservancy; 2014. 42 p.
3. Rohana Tair, Abdullah MH, Noraini A, et al. Heavy metals in the total soft tissues of Geloina similis from mangrove Areas at mengkabong lagoon, Sabah, Malaysia. Proceedings of the 10th Seminar Science and Technology 2012, 1-2 December 2012, Kota Kinabalu, Sabah; 2012:78–84. ISBN:978-983-2641-96-4.
4. Harris RR, Santos MCF. Heavy metal contamination and physiological variability in the Brazilian mangrove crabs, Ucides cordatus and Callinectes danoe (Crustacea: Descapoda). Marine Biology. 2000;137(4):691–703.
5. Tam NFY, Wong YS. Spatial variation of heavy metals in surface sediments of Hong Kong mangrove swamps. Environmental Pollution. 2000;110(2):195–205.
6. MacFarlene GR, Bruchett MD. Toxicity, growth and accumulation relationships of copper, lead, and zinc in the grey mangrove Avicennia marina (Forsk) Vierh. Marine Environmental Research. 2002;54:65–84.
7. Yap CK, Ismail A, Tan SG, et al. Correlations between speciation of Cd, Cu, Pb and Zn in sediment and their concentrations in total soft tissue of Green-lipped Mussel Perna virdis from the West Coast of Peninsular Malaysia. Environment International. 2002;28(1–2):117–126.
8. Tam NFY, Wong YS. Retention and distribution of heavy metals in mangrove soils receiving wastewater. Environmental Pollution. 1996;94(3):283–291.
9. MacFarlane GR. Leaf biochemical parameters in Avicennia marina (Forsk.) Vierh as potential biomarkers of heavy metal stress in estuarine ecosystems. Marine Pollution Bulletin. 2002;44(3):244–256.
10. Google Maps. Mengkabong Lagoon, Malaysia [1:200m]. 2019.
11. Manikandan S. Preparing to analyse data. Journal Pharmacol Pharmacother. 2010;1(1):64–65.
12. Feng CY, Wang HY, Lu NJ, et al. Log-transformation and its implications for data analysis. Shanghai Arch Psychiatry. 2014;26(2):105–109.
13. MacCallum RC, Zhang S, Preacher KJ, et al. On the Practice of Dichotomization of Quantitative variables. Psychological Methods. 2002;7(1):19–40.
14. Rousseeuw PJ, Hubert M. Robust statistics for outlier detection. Wiley Interdisciplinary Reviews: Data Mining and Knowledge; Discovery, 2011;1(1):73–79.
15. Trochim WMK. Descriptive statistics. Research Methods, Knowledge Base; 2006.
16. George D, Mallery M. SPSS for windows step by step: a simple guide and reference. Boston: Pearson; 2010.
17. Noraini A, Zainodin HJ, Ahmed A. Improved stem volume estimation using p-value approach in polynomial regression models. Research Journal of Forestry. 2011;5(2):50–65.
18. Zainodin HJ, Khuneswari G, Noraini A, et al. Selected model systematic sequence via Variance Inflationary Factor. International Journal of Applied Physics and Mathematics. 2015;5(2):105–114.
19. Zainodin HJ, Noraini A, Yap SJ. An alternative multicollinearity approach in solving multiple regression problem. Trends in Applied Science Research. 2011;6(11):1241–1255.
20. Mohammad A, Nghiem SH. Do Instructional Attributes pose Multicollinearity Problems? An Empirical Exploration. Economic Analysis and Policy. 2010;40(3):351–361.
21. Noraini Abdullah, Claudius Mitchell H, Siti Nur Hasliza P. Effect of water parameters on mortality rate of river catfish (Pangasius hypopthalmus) larvae using exponential models with cubic interpolation. Asian J Biol Sci. 2019;12(4):758–764.
22. Noraini Abdullah, Zainodin HJ, Amran Ahmed. Comparisons between Huber’s and Newton’s multiple regression models for stem biomass estimation. Malaysian Journal of Mathematical Sciences. 2012;6(1):1–28.
23. Akaike H. A New Look At the Statistical Model Identification. IEEE Transactions on Automatic Control. 1974;19(6):716–723.
24. Akaike H. Fitting autoregressive models for prediction. Annals of the Institute of Statistical Mathematics. 1970;21(1):243–247.
25. Schwarz GE. Estimating the dimension of a model. Ann Stat. 1978;6:461–464.
26. Hannan EJ, Quinn BG. The Determination of the order of an autoregression. Journal of the Royal Statistical Society. 1979;41(B):190–195.
27. Golub GH, Health M, Wahba G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics. 1979;21(2):215–223.
28. Shibata R. An optimal selection of regression variables. Biometrika. 1981;68(1):45–54.
29. Rice J. Bandwidth choice for nonparametric kernel regression. Annals of Statistics. 1984;12(4):1215–1123.
30. Ramanathan R. Introductory Econometrics with Applications. 5th ed. USA: Harcout College Publishers; 2002.
31. Aminatul HY, Noraini A, Zainodin HJ. Multiple regression models up to first-order interaction on hydrochemistry properties. Asian Journal of Mathematics & Statistics. 2012;5(4):121–131.
32. Glasure Y, Ren L. Applicability of the revised mean absolute percentage errors (MAPE) approach to some popular normal & abnormal independent time series. International Advances in Economic Research. 2009;15(4):409–420.
33. Mulry MH, Oliver BE, Kanuta SJ, et al. A cautionary note on clark winsorization. Survey Methodology. 2016;42(2):297–305.
34. Widmeyer JR, Bendell-Young LI. Influence of food quality and salinity on dietary cadmium availability in Mytilus trossulus. Aquat Toxicol. 2007;81(2):144–151.