The regioselective 1,3-dipolar cycloaddition reactions of acyclic nitrones with norsarkomycin and its analogues have been investigated by density functional theory. The reactivity indices and activation energy calculations were evaluated at B3LYP/6-31G+(d). The reaction path was followed by intrinsic reaction coordinates calculation. Thermodynamic and kinetic parameters of the possible ortho/meta regio-isomeric have been determined in order to illustrate the preferred regioisomer. The obtained results indicate that these reactions mechanism are concerted and both electronic and steric effects describe the regioselectivity of these reactions. The linear variation of the activation energy and Fukui indices as a function of the ring size allows us to predict the characteristics parameters of the reaction between acyclic nitrones and the three-membered analogue of norsarkomycin. These latter were in good agreements with those that have been determined by calculation with the same method.

Keywords: 1,3-dipolar cycloaddition, nitrone, norsarkomycin, density functional theory, fukui function, activation energy

The 1,3-dipolar cycloaddition reaction (1,3-DC) has offered the opportunity to produce a wide range of heterocyclic compounds.^1,2 These compounds were used to prepare new molecules of crucial importance for both pharmaceutics and industry sector.³ The application of 1,3-DC reactions in natural product synthesis is heavily dependent upon an understanding of the regioselectivity and chemioselectivity of the reaction. The regioselectivity of 1,3-dipolar cycloaddition reactions can be determined by electronic structure of reactants, steric factors or combination of both effects.⁴ The aim of this work is to determine the preferred regioisomer (ortho/meta) of the 1,3-cycloaddition reaction between acyclic nitrones and norsarkomycin and its analogues. The effects of N-substituents nitrones on the reactivity of the reaction have been evaluated by global, local reactivity and activation energy.

Actually, the most used theoretical method is the Density Functional Theory (DFT), because it can give very realistic results.^5,6 Recently, DFT studies for the cycloaddition of acyclic nitrones with alkenes became the interest center of several theoretical researchers. In this context, Nivedita Acharjee reported a theoretical study at the DFT B3LYP/6-31G+(d) level of theory of the 1,3-dipolar cycloaddition reactions of an electron deficient C-aryl-N-phenyl nitrone to benzylidene derivatives (with different electrophilicities) and arranged to determine the preferred regioisomer.⁷ In 2016, Mary Mensah and al. achieved a theoretical study on 1,3-dipolar cycloaddition of nitrones to the carbon–carbon double bonds of methylene cyclopropanes with the objective to determine the preferred regioisomer 4- or 5-isoxazolidines.⁸

Our attention will be focused on the effect on the ring size and the N-substituent nitrone on the 1,3-dipolar cycloaddition reaction of nitrones and C-C exocyclic double bond of norsarkomycin and its analogues. The general chemical formula of nitrone is “X-CH=NO-Y”.^9–13 On the first hand, these molecules were first used to snare free radicals in chemical systems and then subsequently in biochemical systems.¹⁴ On the other hand, the sarkomycin is an antitumor antibiotic, isolate from the fermentation liquor of Streptomyces erythrochromogenes by H. Umezawa et al.^15,16 The structure of this compound is 3-methylene-2-oxocyclopentane-1-carboxylic acid.¹⁷

The theoretical DFT methods were used to determine the quantum chemical parameters such as Fukui indices, local and global softness in order to predict the most reactive site. Although, the transition state theory remains the most rigorous approach to study the mechanism and regioselectivity of cycloaddition reactions, the location of the transition states is not always simple. This study will allow us to explain the regioselectivity in different reactions and to determine the most favorable regioisomer (ortho/meta).

All calculations were carried out with GAUSSIAN 09 program package.¹⁸ Geometries of reactants, products and transition states, were optimized using B3LYP functional with 6-31G+(d) basis set.¹⁹ All transition state structures (TSs) were subjected to full frequency calculations to ensure that they have one and only single negative eigen-value, characterized by an imaginary vibration frequency along the reaction coordinate. The intrinsic reaction coordinates (IRC) calculation was done in forward and backward path in order to check the uniqueness specific transition states and draw the reaction path having the minimum energy.^20,21

The studied nitrones can exist into four isomers Z-s-cis, Z-s-trans, E-s-cis and E-s-trans. The Z/E are used for describing the stereochemistry of the double bonds C=N of the nitrones. The s-cis/s-trans are the conformations of a single bond separating two double bonds C=N and C=C (Figure 1).

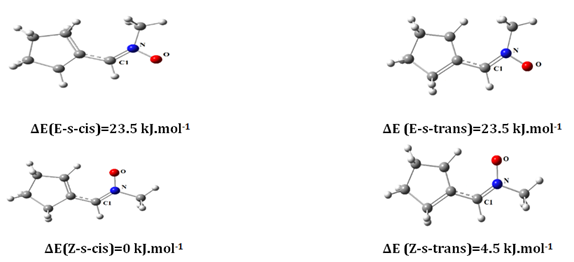
Figure 1 optimized structures geometry for different isomers of nitrone at the B3LYP(6-31)G+(d) level.

From the optimized structures Z-s-cis, Z-s-trans, E-s-cis and E-s-trans several parameters can be explore. In the case of R=CH₃ calculation showed that the Z-s-cis-isomer is the most stable isomer thermodynamically. The abundance of the most stable specie Z-s-cis isomer is equal to 70% and the Z-s-trans 30% for all four compounds at 298 K in gas phase. The relative abundances of the Z- and E-isomers were calculated using the Boltzmann equation:

$K=e^{\frac{-\Delta G}{kT}}$ (1)

Where ΔG denotes the difference between the Gibbs free energies of E-isomer relative to the Z-isomer and K is the Boltzmann constant.²²

Molecular orbital theory

Analysis of frontiers molecular orbitals (FMO) is one of the most popular methods in the study of cycloaddition reaction.²³ According to Fukui functions, the FMO method asserts that the mutual interference between the orbitals of the reactants in the initial phase of the cycloaddition, are generally elements that govern the progress and the regioselectivity of the transformation.²⁴ To get a clear idea, we conducted a global optimization on the geometry of dipoles and dipolarophiles at the same base to explain the regioselectivity and the reactivity in 1, 3-DC reaction of the more reactive nitrone (Z-s-trans) with norsarkomycin and its analogues. To illustrate more this way, we have presented in Figure 2 the two possible interactions: LUMO_{dipolarophile}–HOMO_dipole=ΔE₁ and LUMOdipole–HOMOdipolarophile=ΔE₂. The FMO analysis for these cycloadditions shows that the main interactions occur between the HOMO_dipole and the LUMO_{dipolarophile}, thus, exhibiting normal electronic demand character of the cycloaddition reaction (Tables 1 & 2).

Figure 2 Frontier molecular orbital diagrams of the reactions between the Z-s-trans-nitrone1 and the norsarkomycin and its analogues.

The Fukui functions f(k) are used to describe site selectivity or reactivity of an atom k in a molecule, depending upon the type of electron transfer. This latter can be realized by electronic population analysis.²⁵ We have three different types of condensed Fukui function of the atom k,

$f^{(+)}(k)=q_k(N+1)+q_k(N)$ (2) for nucleophilic attack

$f^{(-)}(k)=q_k(N)+q_k(N-1)$ (3) for electrophilic attack

$f^{(0)}(k)=q_k(N+1)+q_k(N-1)$ (4)

Where q_k(N), q_k(N-1) and q_k(N+1) are the electronic populations of the site k in neutral, cationic, and anionic systems, respectively.

The condensed local softnesses S_k can be easily calculated from the condensed Fukui functions fk and the global softness S(r).^26,27 The local softness sk(r) is defined by:

$S=\frac{1}{{\text{E}}_{\text{LUMO}}-{\text{E}}_{\text{HOMO}}}$ (5)

$s_k^{+}(r)=S{f}_{{{}_{(}}_k{}_{)}}^{+}$ (6)For nucleophilic attack

${\text{s}}_{\text{k}}^{-}\left(\text{r}\right)={\text{Sf}}_{\left(\text{k}\right)}^{-}$ (7)For electrophilic attack

Results of nucleophilic and electrophilic Fukui indices and local softnesses for different sites in nitrones and norsarkomycin and its analogues are summarized in the Tables 3-5.

According to the calculated Fukui functions (Tables 3-5), the oxygen of dipole favors an interaction with C3 of dipolarophile and the carbon C₁ of dipole interact with C₂ of dipolarophile to give the meta-regioisomer, which is the major product obtained by FMO.

The two types of reactants used in these reactions are the electron-donating (ED) (nucleophilic) and electron-withdrawing (EW) (electrophilic) substituents. These substituents were characterized by the presence or absence of electron density in their molecular orbital. The presence of the electron-donating and electron-withdrawing groups defines the direction of flow of electrons between any two or more reacting systems. In this context, EW and ED substituents on either the dipole or the dipolarophile affects the transfer of electrons from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO) of the reacting species according to frontier molecular orbital (FMO) approximation. The possible N-substituent nitrones considered in this work are shown below as R₁=CH₃, R₂=Ph, R₃=CH₂-Ph, R₄=p-Ph-NO₂ and R₅=CF₃ (Figure 3).

The effect of electron-donating and electro-withdrawing groups on the reactivity

Firstly, we would like to talk about the 1,3-DC between the isomer Z-s-trans nitrones (1-5) and the norsarkomycin and its analogues. In this context, we saw previously two types of groups electro-donating and electro-withdrawing. The electron-donating groups considered in this work are (CH₃), (C₆H₅), (C₆H₅CH₂). In each reaction, different combination of R₁, R₂ and R₃ are considered. The easier [3+2] concerted addition pathway was observed for reaction in which R₄ is a p-PhNO₂ group, with activation energy equal to 54.06 kJ.mol^-1 for the meta-isomer. The reaction with the highest activation energy is equal to 79.75 kJ.mol^-1 and corresponding to a methyl and was assigned to the ortho pathway. Therefore, the presence of the electron–donating group increases the activation energy that makes the cycloaddition uneasy. The reactivity of p-PhNO₂ can be explained by the conjugation of the substituent decreasing the E_a probably due to the mesomeric effects.

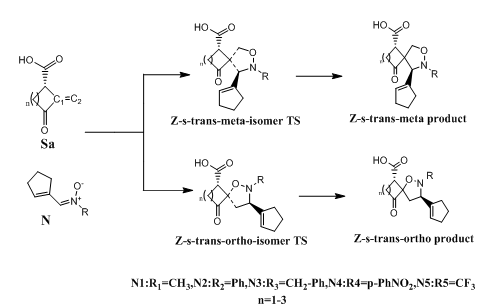
Figure 3 Proposed mechanism for the1,3-dipolar cycloaddition of acyclic nitrones (1-5) with norsarkomycin and its analogues.

Compared to Z-s-trans, the most reactive nitrone is N1 because it is less hindrance substituent comparatively to the other nitrones for the Meta pathway. Besides, for the ortho pathway the N4 is more reactive owing to the mesomeric effects.

The results obtained by FMO, show that the 1,3-DC between norsarkomycin (Sa1) and Z-s-trans N3 displays the smallest value of ΔE so the most reactive nitrone from the FMO is N3. In addition, the FMO indicated that the most reactive Z-s-cis nitrone is N2.

The computational results given in Table 6 show that the 1,3-DC reaction between the Z(s-cis/s-trans) nitrones (1-5) and norsarkomycin and its analogues are under kinetic control.

Regioselectivity

The 1,3-DC reaction was the subject of many studies in order to understand the mechanistic problem in all its complexity. In fact, none of the proposed mechanisms, until now, can be generalized to all the previously discussed work. In our case, and in order to contribute to the subject, we considered a mechanistic approach of the reaction studied by theoretical methods at DFT (B3LYP / 6-31G+(d)) level. Computational studies have been applied to provide that the reactions follow a concerted pericyclic pathway along four possible states; two ortho-isomers states and two meta-isomers.

Reaction between norsarkomycin (Sa1) and (Z)-N-(cyclopent-1-en1-ylmethylene) methanamide oxide (N1): As shown in Table 7 the activation energies associated with the cycloaddition reactions are: 60.71 kJ.mol^-1 (TSm (s-trans)), 79.75 kJ.mol^-1 (TSo (s-trans)), 73.93 kJ.mol^-1 (TSm(s-cis)) and 80.42 kJ.mol^-1 (TSo(s-cis)). Accordingly, it can be predicted that the s-trans-meta regioisomer will be formed preferentially. These values reveal that Meta approaches are favored in regard to ortho ones along the cycloaddition process, in agreement with the FMO analysis. Furthermore, the electronic and thermal free energies indicate that the thermodynamic product is the ortho path for the Z-s-cis-isomer. Therefore, the reactions are under kinetic control (Figures 4-6).

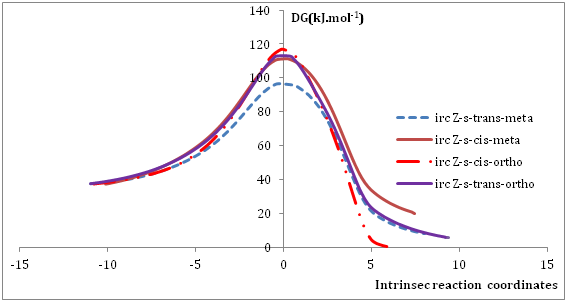
Figure 4 Intrinsic reaction coordinate (IRC) for reactions between Norsarkomycin and different isomers of nitrone1 IRC performed at the B3LYP/6-31G+(d) level.

Reaction between norsarkomycin (Sa1) and (Z)-N-(cyclopent-2-en-ylmethylene)-aniline oxide (N2): In the reaction of N-phenyl substituted nitrone with norsarkomycin (Sa1), the mechanism follows a concerted pericyclic pathway. It produces four transition states structures; Z-s-cis-meta, Z-s-cis-ortho, Z-s-trans-meta and Z-s-trans-ortho isomers. The activation energies associated with the cycloaddition reactions are: 63.14 kJ.mol^-1 (TSm(s-trans), 67.49 kJ.mol^-1(TSo (s-trans), 82.09 kJ.mol^-1 (TSm(s-cis)) and 70.08 kJ.mol^-1 (TSo(s-cis)) respectively. Consequently, it can be predicted that the s-trans-meta regioisomer will be formed preferentially. These values reveal that Meta approaches are favored in regard to ortho ones along the cycloaddition process, in accord with the FMO analysis (Figures 7 & 8). Moreover, for the thermodynamic stability, the most favored product is the Po (Z(s-cis) as shown in Table 8.

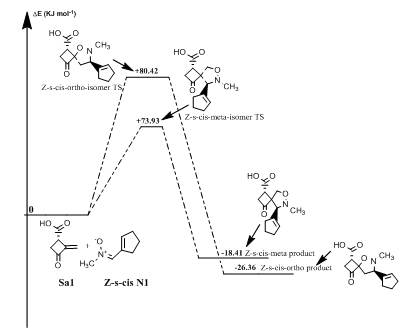
Figure 5 Eneregtic profile of the reaction of  Z-s-cis-isomer N-methyl substituted nitrone with norsarkomycin.

Figure 6 Energetic profile of the reaction of Z-s-trans-isomer N-methyl substituted nitrone with norsarkomycin.

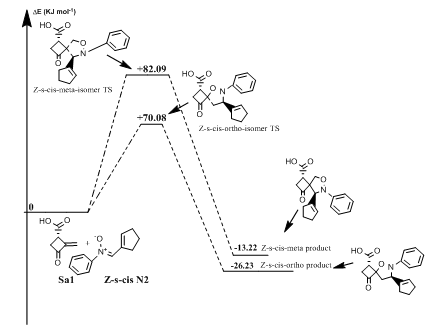
Figure 7 Energetic profile of the reaction of Z-s-cis-isomer N-phenyl substituted nitrone with norsarkomycin.

Figure 8 Energetic profile of the reaction of Z-s-trans-isomer N-phenyl substituted nitrone with norsarkomycin.

Reaction between (Z)-N-(cyclopent-1-en-1-ylmethylene)-1-phenylmethanamine oxide (N3) and norsarkomycin (Sa1): In the case of R=Bn, the activation energy for the formation of Z-s-trans-meta-isomer is 56.06 kJ.mol^-1 whereas that for the formation of the meta-Z-s-cis, ortho-Z-s-trans and ortho-Z-s-cis are respectively 74.60, 64.35 and 69.12 kJ.mol^-1, showing that the meta-Z-s-trans-isomer is kinetically favored over the other-isomers transition states. These values reveal that Z-s-trans-meta approach is favored concerning ortho ones along the cycloaddition process, in agreement with the FMO analysis (Figures 9 & 10).

Reaction of (Z)-(cyclopent-1-enylmethylene)-4-nitroanilineoxide (N4) with norsarkomycin (Sa1): For the 1,3-cycoaddition between Sa1 and N1, the activation energies associated with the cycloaddition reactions are: 54.6 kJ/mol (TSm(s-trans)), 67.11 kJ.mol^-1 (TSo(s-trans)), 81.96 kJ.mol^-1 (TSm(s-cis)) and 68.19 kJ.mol^-1 (TSo(s-cis)) respectively. Consequently, it can be predicted that the meta/s-trans regioisomer will be formed preferentially. These values indicate that Meta approaches are more favored than the ortho ones along the cycloaddition process, in agreement with the FMO analysis. Thus in this reaction, the Po(s-cis) product is 3.9; 6.6; 12.18 kJ.mol^-1 lower in energy than that of the Po(s-trans), Pm(s-trans) and Pm(s-cis) products, favoring the formation of the ortho Z-s-cis-isomer thermodynamically stable (Figures 11 & 12).

Figure 9 Energetic profile of the reaction of Z-s-cis-isomer N-benzyl substituted nitrone with norsarkomycin.

Figure 10 Energetic profile of the reaction of Z-s-trans-isomer N-benzyl substituted nitrone with norsarkomycin.

Reaction of (Z)-N-(cyclopent-1-en-ylmethylene)-1,1,1-trifluoromethanamine oxide(N5) with norsarkomycin (Sa5): The transition states of the reactions between the norsarkomycin and different isomers of N5 prove that the cycloaddition is under kinetic control. Furthermore, the activation energies associated with the cycloaddition reactions are: 59.29 kJ.mol^-1 (TSm(s-trans)), 69.37 kJ.mol^-1 (TSo(s-trans)), 78.37 kJ.mol^-1 (TSm(s-cis)) and 73.09 kJ.mol^-1 (TSo(s-cis)). Therefore, it can be predicted that the Z-s-trans-meta regioisomer will be formed preferentially. These values reveal that Meta approaches are favored in regard to ortho ones along the cycloaddition process. This result is in agreement with the FMO analysis (Tables 6-8). Whereas, the ortho-Z(s-cis)-isomer being more stable by 2.6; 6.7 and 8.9 kJ.mol^-1 than the Po(s-trans), Pm(s-trans) and Pm(s-cis) respectively (Figures 13 & 14).

Figure 11 Energetic profile of the reaction of Z-s-cis-isomer N-para-PhNO2 substituted nitrone with norsarkomycin.

Figure 12 Energetic profile of the reaction of Z-s-trans-isomer N-para-PhNO2substituted nitrone with norsarkomycin.

Methodologies of comparison

One of our main objectives in this study is to determine some properties of the reaction between nitrone and 3-membred analogue of the norsarkomycin (2-methylene-oxocyclopropanecarboxylicacid). If we compare the values of $f_k^{+}$₂E@  (C₂) and $s_k^{+}$  (C₂) deduced from the linear variation as shown Figure 15 and calculated theoretically (Table 9), the two ways give close result. Therefore, the meta-regioisomer is more favorable than the ortho-path.

From Figure 16 it can be predicted the values of activation energies correspond to the reactions between nitrone1 and Z-s-cis Sa5 and Z-s-trans Sa5 respectively are equal to 71.65 kJ.mol^-1 and 56.79 kJ.mol^-1. For the DFT mechanistic studies, we have fully optimized the transition states structures of the reaction between Sa5 and the (Z-s-trans/Z-s-cis) nitrone1 isomers; we have obtained activation energies of values respectively: 60.4 kJ.mol^-1 for (s-trans) and 73.23 kJ.mol^-1 for Z-s-cis-meta isomer.

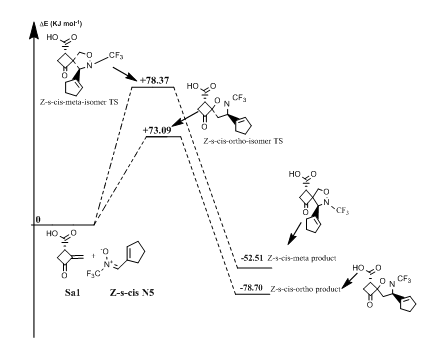
Figure 13 Energetic profile of the reaction of Z-s-cis-isomer N-CF3 substituted nitrone with norsarkomycin.

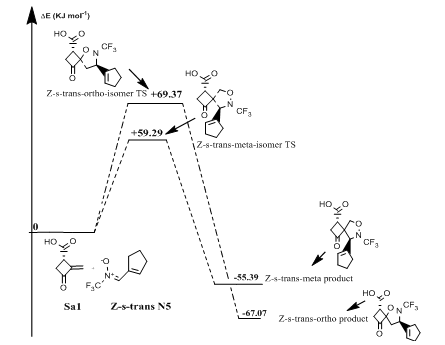
Figure 14 Energetic profile of the reaction of Z-s-trans-isomer N-CF3 substituted nitrone with norsarkomycin.

Figure 15 Variation of electrophilic Fukui indices and local softness for (C₂) as a function of ring size for the norsarkomycin and its analogues.

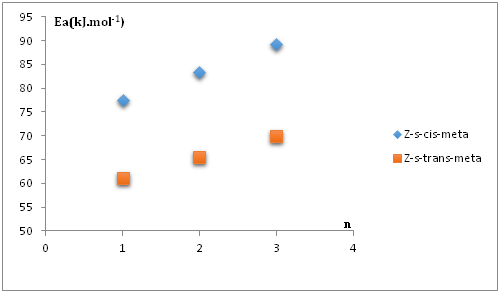
Figure 16 Variation of activation energy as a function of ring size for the 1,3-cyloaddition between Z-s-trans and Z-s-cis nitrones1 and the norsarkomycin and its analogues(meta regioisomer).

We have examined in the present theoretical study, the regioselectivity of the 1,3-dipolar cycloaddition reaction of the acyclic nitrone with the norsarkomycin and its analogues by both FMO analysis, activation energy, global and local reactivity at DFT/B3LYP level using the 6-31G+(d) basis set. This study reveals that the Z-nitrones are more abundant than E-nitrones. According to the analysis of FMO, energies and charge transfer at the transition states indicate that all these reactions are concerted and are with normal electron demand character. In addition, for the reactions between N-substituents nitrone with the norsarkomycin and its analogues; the meta-pathway is favored both kinetically over ortho-isomer in all cases. The results show a clear preference for the meta- regioselectivity of the cycloaddition process in conformity with FMO. Therefore, the selectivity of the reactions was governed solely by the difference in activation energies leading to the two isomers and not in any way by the thermodynamic stability of the isomers formed. The linear variations of some properties as function of ring size allow us to predict some characteristics of the reaction between nitrone1 and 3-membred analogue of norsarkomycin, which has not been synthetized. We have found that the reactivity of the 1,3-cycloaddition reaction between nitrones and norsarkomycin and its analogues is a decreasing function with the ring size.

None.

The author declares no conflict of interest.

1. Merino P, Revuelta J, Tejero T, et al. A DFT study on the 1,3-dipolar cycloaddition reactions of C-(methoxycarbonyl)-N-methyl nitrone with methyl acrylate and vinyl acetate. Tetrahedron. 2003;59:3581–3592.
2. Padwa A , Bur S. Chapter nine-recent advances of 1,3-Dipolar cycloaddition chemistry for alkaloid synthesis. Adv Heterocycl Chem. 2016;119:241–305.
3. Padwa A, Bur S. Synthetic application of 1,3,-dipolar cycloaddition chemistry toward hetero cycles and natural products. nitrones. 2003;59:1–181.
4. Schoenebeck F, Ess DH, Jones GO, et al. Reactivity and regioselectivity in 1,3-dipolar cycloadditions of azides to strained alkynes and alkenes: A computational study. J Am Chem Soc. 2009;131(23):8121–8133.
5. Becke AD. Density‐functional thermo chemistry. III. The role of exact exchange. J Chem Phys. 1993;98(7):5648.
6. Stecko S, Pas´niczek K, Michel C, et al. A DFT study of 1,3-dipolar cycloaddition reactions of 5-membered cyclic nitrones with a,b-unsaturated lactones and with cyclic vinyl ethers: Part1. Tetrahedron: Asymmetry. 2008;19:1660–1669.
7. Acharjee N. DFT interpretations for cycloadditions of an electron deficient C-aryl-N-phenyl nitrone. J Theo and Comp Chem. 2014;13:1450007–1450019.
8. Mensah M, Amepetey EE, Richard T, et al. 1,3-Dipolar [3+2] Cycloaddition Reactions of N, C, C-trisubstituted nitrones with ring-acceptor methylenecyclopropanes: a computational study. Springerplus. 2016;5:2072–2079.
9. Merino P, Tejero T , Delso I, et al. New mechanistic interpretations for nitrone reactivity. Org Bio Chem. 2017;15(16):3364–3375.
10. Jasinski R. Competition between the one-step and two-step, zwitterionic mechanisms in the [2+3] cycloaddition of gem-dinitroethene with (Z)-C,N-diphenylnitrone: a DFT computational study. Tetrahedron. 2012;69:927–932.
11. Hashimoto Y, Ishiwata H, Tachikawa S, et al. Utilization of electron-donating α,β-unsaturated oximes: regioselective inverse 1,3-dipolar cycloaddition of nitrones. Chem Commun. 2017;53(18):2685–2688.
12. Juste-navarro V, Delso I, Tejero T, et al. Stereoselective Cycloaddition of Nitrone Ylides with Aldehydes using n-BuLi. Chem Eur J. 2016;22:11527–11532.
13. Floyd RA, Hensley K, Forster MJ, et al. Nitrones, their value as therapeutics and probes to understand aging. Mech Ageing Dev. 2002;123(8):1021–1031.
14. Floyd RA, Hensley K, Forster MJ, et al. Nitrones as neuroprotectants and antiaging drugs. Ann N Y Acad Sci. 2002;959:321–329.
15. Floyd RA1, Kopke RD, Choi CH, et al. Nitrones as Therapeutics. Free Radic Biol Med. 2008;45(10):1361–1374.
16. Umezawa Y, Yamamoto T, Takeuchi T, et al. Sarkomycin an anti-cancer substance produced by streptomyces. Antibiotics & Chemotherapy. 1954;4:514–520.
17. John NM, Minaskanian G. Regiospecific synthesis of sarkomycin and some analogues. J Org Chem. 1982;47(17):3307–3310.
18. Vidal J, Huet F. Synthesis of α-Methylenecyclobutanones: the first preparation of norsarkomycin methyl ester. J Org Chem. 1988;53(3):611–616.
19. Frisch M J, Trucks G W, Schlegel H B, et al. Electronic supplementary material (ESI) for chemical science. J Royal society of chemistry. Gaussian 09, Wallingford, UK: Gaussian Inc; 2010.
20. Arfaoui Y, Efrit M L, Besbes N. Theoretical investigations on the mechanistic pathway of the thermal rearrangement of substituted N-acyl-2,2-dimethylaziridines. J Mol Model. 2013;19(10):4603–4612.
21. Mökkönen H, Ala-Nissila T, and Jónsson H. Efficient dynamical correction of the transition state theory rate estimate for a flat energy barrier. J Chem Phys. 2016;145(9):094901.
22. Fukui K. The path of chemical reactions-the IRC approach. Acc Chem Res. 1981;14(12):363–368.
23. Lasri J, Eltayeb N E, Haukka M, et al. Crystal and molecular structure studies of (Z)-N-methyl-C-4-substituted phenyl nitrones by XRD, DFT, FTIR and NMR methods. J mol struc. 2016;8:058.
24. Marakchi K, Ghailane R , Kabbaj O K, et al. DFT study of the mechanism and stereo selectivity of the 1,3-dipolar cycloaddition between pyrroline-1-oxide and methyl crotonate. J Chem Sci. 2014;126(1):283–292.
25. Geittner J, Huisgen R. Kinetics of 1,3-dipolar cycloaddition reactions of diazomethane; A correlation with homo-lumo energies. 1997;18:881–884.
26. Acharjee N, Banerji A. DFT interpretation of 1,3-dipolar cycloaddition reaction of C,N-diphenyl nitrone to methyl crotonate in terms of reactivity indices, interaction energy and activation parameters. Comput and Theo Chem. 2011;967(1):50–58.
27. Fakhar Z, Govender T, Lamichhane G, et al. Computational model for the acylation step of the b-lactam ring: Potential application for L,D-transpeptidase 2 in mycobacterium tuberculosis. J Mol Struct. 2017;1128:94–102.