The flow of fluid nearby two circular staggered cylinders of identical size was investigated using computational flow dynamics (CFD). The center-to-center pitch ratio was taken constant, P/D = 2, and the incidence angle (α) was changing from 0° to 90°. Reynolds number (Re) used during the simulation was 300. This Re belongs to the periodic vortex shedding regime. Navier-Stokes equation was used to solve this unsteady flow problem in Two-dimensional incompressible form. Gambit 2.2.3 was used for the development of flow geometry configuration was as it allows imposing the boundary conditions of flow domain with ease. The flow field of staggered arrangement experimented evaluated experimentally in literature for five cases, namely, shear-layer-reattachment (SLR) for α = 0º, vortex pairing and enveloping (VPE) for α = 45º, vortex pairing, synchronized vortex shedding (SVS) and splitting for α = 90º was predicted using numerical model successfully.

Keywords: staggered cylinder, CFD, shear layer reattachment, finite element analysis, unsteady flow

P/D, pitch to diameter ratio (center to center distance);α, angle of incidence; Re, reynolds number; SLR, shear-layer-reattachment; VPE, vortex-pairing and enveloping; SVS, synchronized vortex shedding; St, strouhal frequency; R, reattachment; Lx, x-dimension of domain; Ly, Y- Dimension of domain; NX, no. of grids in x dimension; Ny, No. of grids in y dimension; SIMPLE, semi-implicit method for pressure linked equations; ωz, spanwise vorticity; T, time period of vortex shedding; VPSE, vortex-pairing-splitting-enveloping; P∞, free-stream pressure; Cp, coefficient of pressure; CD , coefficient of drag; v, normal velocity; u, stream wise velocity; PSD, power spectra density

The flow around bluff bodies, vortex formation, mechanisms of flow separation, the behaviour of the wake, and fluid-structure interactions are widely discussed.¹ The flow around bluff bodies of cylindrical shape has been studied considerably owing to its engineering importance in designing structures, acoustic emission dynamics, and fluid flow-induced vibration.^2–9 The bridge constructions, ad hoc defence structures, offshore platforms, tall buildings, heat exchangers, electrical transmission lines could break due to the vibration and oscillatory force; therefore, analysis of cylinder wake is significant. The rotation,^10–12 and utilization of auxiliary device,^13–15 are commonly employed methods for controlling the flow around an isolated cylinder. A summary of more than 20 studies reported experimental investigations on flow pattern identification for circular staggered cylinders in a cross flow is presented.¹⁶ Further, the numerical studies on this topic were summarised in (Figure 1).^{17, 18} shows the summary of flow patterns for 2 staggered cylinders of the same radius in steady crossflow.¹⁶

Figure 1 Overview of flow patterns for 2 circular staggered cylinders of equal diameter in steady cross-flow, based on:¹⁶ (a) closely spaced; (b) moderately spaced; (c) widely spaced. R=reattachment; G=gap.

The present work aimed to determine the capability of numerical model for the prediction of flow patterns for two circular staggered cylinders considering a variety of Reynolds numbers and configurations. The validation of the model was performed with experimental data presented in the literature. The work defines the limitation of commercial modules while reviewing the widely discussed problem undertaken in the present study.

The momentum equation, continuity equation, and energy equation,^19–21 are the governing equations for the present work. Ansys-Fluent 14.5 software was utilized to simulate flow over a pair of staggered cylinders for constant pitch and different angles of incidences at a constant Re=300 initially. Further, the capacity of model was evaluated for higher Reynolds numbers. The 2-D geometrical model of circular cylinders has been drawn up with geometrical detail taken from,²² the experimental results of, ²² were utilized for the justification of numerical model. The computational domain, details of boundary conditions and governing fluid flow equations are taken from,²² the viscous-laminar and incompressible flow were considered. (Figure 2) shows the three different cases solved in the present work, where P/D=2 was fixed for all cases. The α was varying from 0° to 90°. The Cartesian grid, a refined and uniform mesh were used in the stream-wise direction, nearby the cylinder, to get acceptable immersed boundary points on the surface of the cylinder. Considering the origin of the axes lies the centre of the upstream cylinder and at a distance -7.5D in stream-wise direction and -7.5D in transverse direction. The coordinates x,y denoted the stream-wise and transverse direction respectively and the corresponding velocities u,v.

Figure 2 Cylinder arrangements in the flow domain.

The boundary conditions for the computational domain are shown in Table 1 and (Figure 3). The boundary conditions of wall are used to bound solid and fluid zones. The no-slip boundary condition was enforced at walls in viscous flows, which states that the flow velocity in x, y and z-direction is 0 i.e. u=0, v=0, w=0. The boundary condition was employed to the surface of both cylinders.

Figure 3 Flow domain and boundary condition for the tandem arrangement (P/D=2, α=0°).

Since the flow is purely one dimensional hence no flow exists in y and z-direction. U∞=1(non-dimensional), v=w=0 at the inlet, outflow boundary conditions in fluent 14.5 is used to model flow exist where the details of the pressure and flow velocity are unknown before the solution of the flow problem.

The domain spreads from -7.5D at inflow to 25D at the outflow with and -7.5D to +7.5D in cross flow direction, considering the origin of the area lies at the centre of the upstream cylinder. The boundary conditions include velocity inlet, pressure outlet, symmetry (free-slip boundary condition) at the lower and upper domain, and wall boundary condition (no-slip boundary condition, u=v=0) on both the cylinder’s surfaces. Cartesian grid is used for the simulation for flow nearby two circular cylinders in unbounded condition. A grid independence test was performed at α=0° before selecting the final grid. Three different grid levels have been chosen considering the same domain. For grid 1, a total of 344×152 grid points are used in x and y directions, respectively, whereas for grid two and grid three the total number of grid points is 440×200 and 524×236 respectively. From this test, it appears that grid two and grid three generate almost identical results (as given in Table 2), and therefore grid level 2 has been for further analysis.

In detail, a box 4D×2D is considered surrounding both the cylinders where small and equal meshing use to properly resolve the boundary layers over the cylinders. Outside this box, meshes are slowly stretched out in all directions. The 304×160 mesh elements were used for tandem cylinders (α=0°), for intermediate case (α=45°), grid points are distributed as 304×164 for VPE, while a mesh of 240×224 is used for side-by-side cylinders (α=90°). In the wake region (x/D = 3 to 20 and y/D=0 to ±2 after downstream cylinder), non-dimensional mesh spacing varies as Δx=(0.0546 - 0.25) and Δy=(0.031 - 0.072) for all cases which is quite good to resolve the interacting vortices. The computations are carried out using Fluent 14.5, which uses a finite volume approach to discretized governing and model equations for incompressible laminar flow. The solver is used pressure-based solver in steady-state with absolute velocity formulation for planar 2-D space. In Fluent, viscous laminar model is considering along with air as the fluid. The equations are spatial discretization using gradient is Least Square Cell-Based, pressure is Standard, and momentum is Second-Order Upwind with the pressure-velocity coupling use SIMPLE algorithm scheme to solve the Navier-Stokes equation. The meshed geometry of the staggered cylinders in α=0°,45°, and 90° is as shown in (Figure 4–6) respectively, where the structured meshing is shown in the zoomed view also.

Flow over a pair of staggered cylinders are simulated using Fluent for a fixed pitch ratio P/D=2 with varying incidence angles (α =0°,45°,90°) at a low Reynolds number (Re =300) in periodic vortex shedding regime. The obtained results are extensively compared with previous experiments and numerical studies, particularly with Sumner et al.,²² who performed their investigations for a wide range of pitch ratio (P/D=1 to 5) and angle of incidences (α=0° to 90°) considering Re in the shear layer transition regime (Re=850-1900). Although present computation is performed at a reasonably low Re (Re=300) as compared to them, the basic flow features about the cylinders and near wake region almost remain same. As the Reynolds number used in present work lies in the unsteady laminar periodic vortex shedding regime, the time-averaged measures of the flow parameters are premeditated over approximately 20 vortex shedding cycles after the flow field becomes dynamically steady. Later, flow characteristics were compared for Reynolds numbers up to 10⁴.

A

B

Figure 4(A) The meshing of the circular cylinders in a tendem arrangement (α=0°), (B) The zoomed view of the meshing close around to the circular cylinders (α=0°).

A

B

Figure 5(A) The meshing of the circular cylinders in a tendem arrangement (α=45°), (B) The zoomed view of the meshing close around to the circular cylinders (α = 45°).

A

B

Figure 6(A) The meshing of the circular cylinders in a tandem arrangement (α=45°), (B) The zoomed view of the meshing close around to the circular cylinders (α=45°).

For visualizing the vortex dynamics of two cylinders during a shedding cycle, the snaps of iso-counters of spanwise vorticity (ωz) are presented in (Figures 7–9) for a different angle of incidences. The time (T) of vortex shedding was calculated with the help of the Strouhal number (St). An explanation for the vortex formation from both the cylinders, their downstream convection, and interaction with each other are adequately described following the experimental study of Sumner et al.,²² although performed at different ranges of Re. Figure 7 illustrates that for tandem cylinder arrangement, flow in between two cylinders is prevented by the formation of separated shear layers formed by the upstream cylinder. These shear layers from both sides of the upstream cylinder reattach with the respective shear layers of the downstream cylinder and this kind of flow pattern can be termed as shear layer reattachment.²² In between the cylinders, a very low-pressure zone is created attributed to negligible flow and produces a separation bubble. The elongated shear layers from both side of the downstream cylinder, stagnant gap flow and Karman Vortex Street are properly described in (Figure 7).

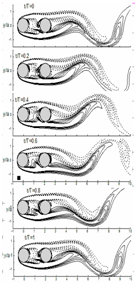
Figure 7 Instantaneous vorticity contours for cylinders in tandem arrangement (P/D = 2, α=0°). Six non-dimensional contours are taken between -1 and +1. The dotted line shows negative vortices.

For the intermediate gap ratio (α=45°), it is quite challenging to say whether the flow patterns belong to VPE or VPSE. The instantaneous vorticity pictures for different time-frame illustrate the vortex pairing, encompassing along with excessive stretching of the lower shear layer of the upstream cylinder for α=45° (Figure 8).

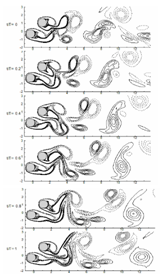
Figure 8(A) Instantaneous vorticity contours for cylinders in staggered arrangement (P/D=2 at α=45°). For details refer Figure 7.

The synchronized vortex shedding (SVS) which can be seen for P/D=1.5 to 5 and α=15° to 90° (Sumner et.al.,²²) is also can be seen for the present case of P/D=2 and α=90° (Figure 9). The anti-phase synchronization of gap Karman vortices occurs at t=0 and t=T frame. As shown in the figure, an upward gap flow is visible between two side-by-side cylinders at t=0, and the gap flow direction becomes downward just after one time (t=T). The flow visualization of the present simulation almost mimics the experimental flow field,²² although performed at different range of Re and for different geometrical configurations.

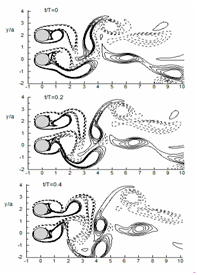
A

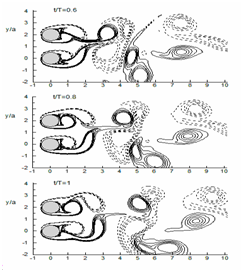
B

Figure 9 Instantaneous vorticity contours for cylinders in staggered arrangement (P/D=2 at α=90°). For details, refer Figure 7.

Instantaneous spanwise vorticity

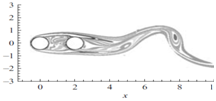
(Figure 10) represents the comparison of instantaneous span-wise vorticity (ωz) of the numerical simulation of¹¹ performed at Re=500 and present work when the cylinders are in tandem position (α=0°). Sumner et al.,²² characterized this flow pattern as shear layer reattachment when pitch ratio is small (P/D<3) and angle of incidence α is below 10°. Here, flow through the gap between the cylinders was prevented by the development of separated shear layers from both sides of the upstream cylinder. These shear layer from the upstream cylinder stretched over the downstream cylinder surface and reattached with its shear layers. (Figure 10) reveals that present computation is in good agreement with the previously published result although performed at different Re.

A

B

Figure 10 (A) Instantaneous span-wise vorticity (ωz) (a) at Re = 500, P/D = 2 at α=0°, Papaioannou et al.,¹¹ (B) at Re = 300, P/D=2 at α = 0°, present simulation.

Previously, the shear-layer reattachment process has been taken as a steady phenomenon. Steady reattachment was perceived for square and triangular clusters of circular cylinders at incidence, by Lam and Cheung.,²³ and Lam and Lo.,²⁴ in a similar range of low subcritical Re. In disparity, shear-layer reattachment for the tandem arrangement of cylinders, where α=0°, happens in a sporadic, episodic fashion, in harmonization with Karman vortex shedding from the downstream cylinder.^25–30

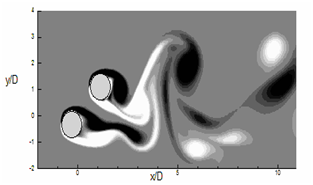
(Figure 11) illustrates the flow characteristics change as the configuration of the two cylinders changes. The iso-surfaces of instantaneous span-wise vorticity for the staggered arrangement are shown in (Figure 11) to envisage the flow structures, which are equated with the experiment of Sumner et al.,²² The figure reveals that the shear layers from the upstream cylinder don’t have adequate space to roll-up entirely before being entrained into the wake of the downstream cylinder. The shear layers from the downstream cylinder form consistent Karman vortices nearly without disruption. Nearby the wake region of the downstream cylinder, the negative vortices from the inner shear layer of the upstream cylinder pair-up with the positive vortices from the inner portion of the downstream cylinder and the outer shear-layer of the upstream cylinder moderately enveloped this vortex pair. Apart from the outer and inner shear layers of the upstream cylinder, the third row of vortices appears mainly due to splitting of the vortex pair. Sumner et al.,²² first identified this kind of flow pattern with modest pitch ratio (1≤P / D≤2) and high angle of incidence (α ≥300) and named it VPSE (vortex pairing, splitting and enveloping) flow pattern.

A

B

Figure 11 Instantaneous span-wise vorticity (ωz) contours (A) Experiment of Sumner et al.,²² at Re=850, P/D=2, α=45°, (b) Present simulation at Re =300, P/D =2 at α =45°.

Contour of coefficient of pressure with streamlines

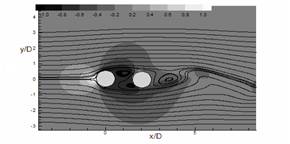
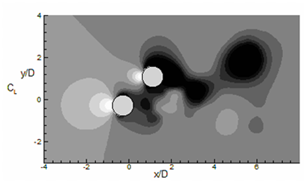
The contours of instantaneous pressure coefficients $(C_p)$

$C_P=\frac{P-P_{\infty }}{\frac{1}{2}\rho U_{\infty }^2}$

Where, P_∞ represents the free-stream pressure of flow over the circular cylinders for Re=300 as presented in

(Figure 12)

A

B

C

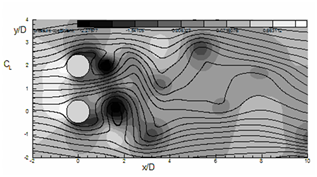
Figure 12 Instantaneous pressure coefficient (Cp) contours represented by flood diagram. Total 6 non-dimensional contours are drawn between -1 and + 1. Lines show instantaneous streamlines. (a) α = 0°, (b) 45° and (c) 90°.

Lift and drag coefficients

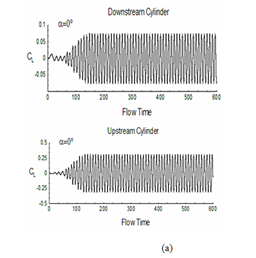
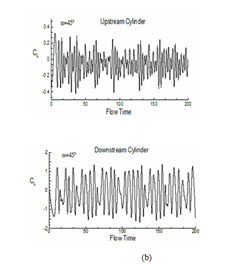
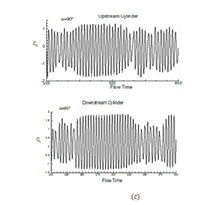
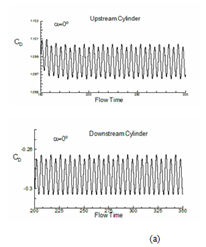
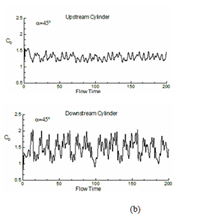
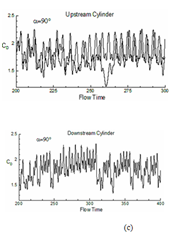
For understanding the change in aerodynamics forces for both downstream and upstream cylinders, the evolution of coefficient of lift (C_L) and drag (C_D) with flow time is depicted for α = 0° to 90° in fig. 14 and 15. The figure indicates that as the angle of incidence between the two cylinders increases, the level of fluctuation of lift also increases. The average value of coefficient of lift$({\overline{C}}_L)$ for upstream cylinder comes as 0, 1.060, 0.638 for α=0°, 45° and 90°. For downstream cylinder these values are 0, 0.10, 1.795 respectively (refer table 3). Mean drag coefficient $({\overline{C}}_D)$ for the above mention angle of incidences are 1.427, 0.267, 1.795 for upstream cylinder and -0.113, 1.365, 0.217 for downstream cylinder. These results indicate negative mean lift for upstream cylinder and positive lift for downstream cylinder as obtained by other researchers.^{14–16,31,32} A continuous increase in $({\overline{C}}_D)$ (for both downstream and upstream cylinders) the increase of α for a constant pitch ratio is a significant finding in case of a pair of cylinders.^33–40

Time average spanwise vorticity

The time average flow field of the staggered cylinders at different angle of incidences (α=0°, 45°, 90°) are depicted in this section to get an understanding of the mean flow field. This is obtained by considering the average data of the flow field for a time period of 2T.

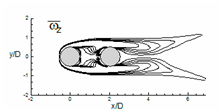
(Figure 16) represents the average vorticity (ωz) field of the staggered cylinder pair. For α=0°, in a tandem arrangement, the vorticity contour represents symmetrical shape concerning the horizontal cylinder axis. The effect of vorticity is mainly spread in the stream wise direction and can be felt up to x/D =7. For α=45° (Figure 16B) the ωz values show interaction of vortices from the upper layer of upstream cylinder and lower layer of the downstream cylinder. For this interaction now, the vortices are not symmetrical concerning the cylinder axis. For side by side cylinders (Figure 16C) the vortices are synchronized concerning each other and remain symmetric. The fluctuation in the flow field suggests, there is a need for more time to calculate the average vorticity.

A

B

C

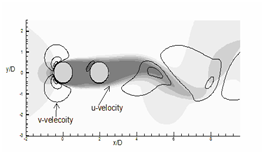
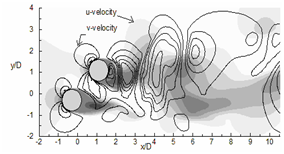
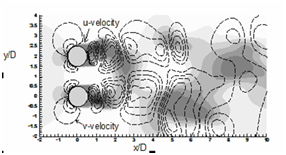
Figure 13 Instantaneous stream-wise velocity (u) contours are represented by flood diagram and instantaneous transverse velocity (v) contours are represented by line diagram. Dotted lines are '-ve' v-contours. For both velocities total 6 non-dimensional contours are drawn between -1 and + 1. (a) α = 0°, (b) 45° and (c) 90°.

A

B

C

Figure 14 Evolution of coefficient of lift (CL) with flow time both for upstream and downstream cylinders: (a) α=0°, (b) 45° and (c) 90°.

A

B

C

Figure 15 Evolution of coefficient of drag (CD) with flow times both for upstream and downstream cylinders: (a) α=0°, (b) 45° and (c) 90°.

A

B

C

Figure 16 Evaluation of time average spanwise vorticity for circular staggered cylinders at α=0°, α=45°, α=90°.

Mean of streamlines over cylinders

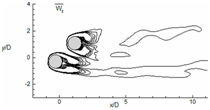
Figure 17 illustrates the mean streamline plot for all cases; here for tandem cylinders, the streamlines plots are symmetrical concerning the cylinder axis. It shows the presence of separation bubble in the downstream of both the cylinders.¹⁷ The first bubble occupies the full gap between both the cylinders, whereas the size of second bubble is smaller. With increase in angle of incidence (α=45°), the separation bubble size reduces for both the cylinders, and accelerating flow can be seen between the narrow passage of the cylinder from the streamline plot. At (α=90°), the gap between the cylinder increases through which fluid flow occurs properly. The separation bubble size n the downstream of cylinder reduces further. The streamline plot of the cylinders remains identical.

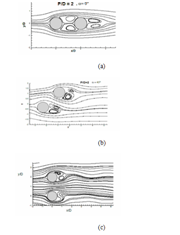
Figure 17 The streamlines of flow over cylinders are shown for (a) α=0°, (b) α = 45° and (c) α = 90°.

Time average of coefficient of pressure

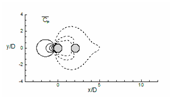
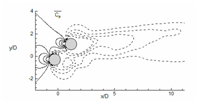
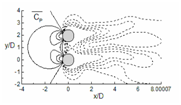
The mean pressure coefficient contours are shown in figure 18, for all cases. Cp plot at α = 0°, show the definite contours at front stagnation point of the upstream cylinder (extreme left point of the upstream cylinder) and negative contours in the downstream region. Therefore, the downstream cylinder is wholly immersed in negative pressure contour which changes the flow field in comparison to a single cylinder. At α = 45° (fig. 18 (b)), positive mean coefficient of pressure contours occurs at front stagnation point of both the cylinders and negative contours in the downstream direction. The mean Cp contour for α = 90° (fig. 18 (c)) is symmetrical for both the cylinders as compared to each other, and here also positive mean coefficient of pressure can be seen at front stagnation point of the cylinders. The negative contour is extended in far downstream illustrates prominent vortex shedding in this case.

A

B

C

Figure 18 Evaluation of time average of coefficient of pressure (Cp) for (a) α=0°, (b) α=45° and (c) α=90°.

Time average flow field for U velocity and V velocity

The mean transverse velocity (v̄) and mean streamwise velocity (ū) contours are plotted in (Figure 19). For tandem cylinders, negative ū contour in between the cylinder represents the separation bubble, and positive ū velocity in downstream direction describes convection of vortices in the downstream direction. The v̄ contour is symmetrical concerning the cylinder axis. As the angle of incidence increases, the interaction between the vortices of the downstream and upstream cylinder also increases which is evident from the ū and v̄ plot at α=45° (Figure 19B) and α=90° (Figure 19C).

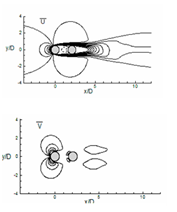
A. Time average flow field for U velocity and V velocity at α=0°.

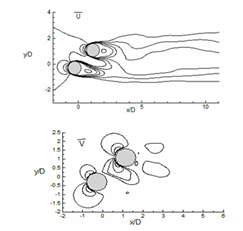
B. Time average flow field for U velocity and V velocity at α=45°.

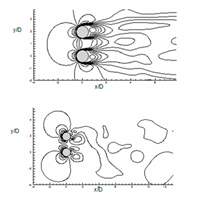
C. Time average flow field for U velocity and V velocity at α = 90°.

Figure 19 Evaluation of time average of flow for U velocity and V velocity for (a) α=0°, (b) α = 45° and (c) α=90°.

Vortex shedding frequency

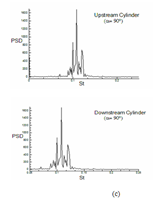
The power spectra density (PSD) along with Strouhal number (St) for cases (α=0°, α=45°and α=90°) are depicted in (Figure 20). The spectra have drawn by collecting the data of C_L over 10 non-dimensional times, the St values obtained from the significant peak in all are enlisted in Table 3 both for upstream and downstream cylinders. As per Sumner et al.,²² vortex shedding frequencies are more appropriately associated with individual shear layer than with single cylinder; but in the present simulation we calculated St values for a single-cylinder from the time evolution of C_L.

A

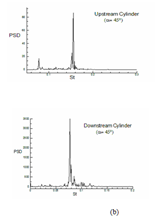
B

C

Figure 20 Power spectra density (PSD) with Strouhal number (St) both for upstream and downstream cylinders: (a) α=0°, (b) α=45° and (c) α=90°.

When the cylinders are aligned inline (α=0°) a single peak is obtained for both the cylinders (at St=0.05). The changes in flow behavior at intermediate value of α (α=45°) can be attributed to the presence of two peaks in PSD diagram. For α=45°, major and minor peaks occur at St =0.078, 0.08 in case of upstream cylinder. The presence of multi-peaks for both cylinders at α=90° can be attributed to the anti-phase synchronization of gap vortex shedding associated with side-by-side cylinders showing in Figure 20. The present results are in good agreement with the Ref.²² although performed at different Re. For Reynolds number 10⁴, error and deviations were significant due to limitations of the turbulence models; thus results were not reported in the manuscript.

Flow simulations of the wake behind two circular cylinders of equal size placed in staggered arrangements (P/D=2, α=0° to 90°) are studies extensively at unsteady laminar vortex shedding regime (Re=300). The computation is carried out in Ansys Fluent 14.5, and instantaneous flow physic is described widely. It has been observed that the present computational cases are matched quite well with the flow characteristic described by Sumner et al., although their experiments were conducted at a subcritical range of Reynolds number with circular cylinders. This reveals Fluent is capable of describing wake-wake interactions at least for low Re flow. Three flow patterns were recognized in this part of low subcritical regime. The incidence angle boundaries and pitch ratio for the flow patterns were projected. Significant features of the flow consist of vortex pairing and synchronization, shear layer reattachment, and synchronized vortex shedding. In some cases, minimal changes in the incidence or direction of the approaching flow, resulting in a considerably different flow pattern.

1. For P/D =2 and α=0° (tandem arrangement), the flow feature comes under shear layer reattachment (SLR) group, where the shear layers from the upstream cylinder reattach with the shear layers of the downstream cylinder with a stagnant fluid and a low level of vorticity in between the cylinders
2. For P/D=2 and α=45°, the flow characteristics come under vortex pairing and enveloping (VPE). Two rows of vortices describe this flow pattern in the combined wake of the cylinders.
3. For P/D=2 and α=90°, the flow behaves like synchronized vortex shedding (SVS), manifest by flow from the gap in the cylinders that is glanced away from the flow-axis, resulting in two different widths of near-wake regions, and two dominant frequencies of vortex shedding.

The results of numerical model are in good agreement with experimental results of Sumner et al.,²² although their experiments were conducted at sub critical range of Reynolds number with circular cylinders. The model has predicted effectively for the high range of Re including the shear layer transition regime. Here, the instantaneous vortex dynamics for the staggered configuration are conversed systematically along with Strouhal frequency (St) and aerodynamics forces. The numerical model was capable of generating similar results for the laminar periodic-vortex-shedding regime.

The first author is grateful to Mr. MK Shukla, Senior Scientist, CSIR-IIP Dehradun for his guidance. The corresponding author acknowledges financial support of IAAM, Sweden and VBRI, Delhi.

The author declares that there are no conflicts of interest.

None.

1. Vedrtnam A, Pawar SJ. Experimental and simulation study on bending cyclic fatigue behavior of laminated glass having Polyvinyl Butyral and Ethyl Vinyl Acetate inter-layers. Fatigue Fract Eng Mater Struct. 2018;41(6):1437–1446.
2. Vedrtnam A, Anuj Kumar. Fabrication and wear characterization of Silicon Carbide and Copper reinforced Aluminum matrix composite. Material Discovery. 2017;9:22.
3.  Jorge Pereira Gomes, H Lienhart. Fluid–structure interaction – induced oscillation of flexible structures in laminar and turbulent flows. J Fluid Mech. 2013;715:537–572.
4. Puneeshwar Lal Verma, M Govardhan. Flow behind bluff bodies in side-by-side arrangement. Journal of Engineering Science and Technology. 2011;6(6):745–768.
5. PW Bearman. Vortex Shedding from Oscillating Bluff Bodies. Annual Review of Fluid Mechanics. 2003;16(1):195–222.
6. Williamson CHK. Vortex dynamics in the cylinder wake. Ann Rev Fluid Mech. 1996;28:477–539.
7. Prasad A, Williamson CHK. The instability of the separated shear layer from a bluff body. Phys Fluids. 1996;8:1347–1349.
8. Gu ZF, Sun TF. On interference between two circular cylinders in staggered arrangement at high subcritical Reynolds numbers. J Wind Eng Ind Aerodyn. 1999;80:287–309.
9. Gu ZF, Sun TF. Interference between wind loading on group of structures. J Wind Eng Ind Aerodyn. 1995;54:213–225.
10. Kiya M, Arie M, Tamura H, et al. Vortex shedding from two circular cylinders in staggered arrangement. J Fluids Eng. 1980;102:166–173.
11. Price SJ, Païdoussis MP. The aerodynamic forces acting on groups of two and three circular cylinders when subject to a cross-flow. J Wind Eng Ind Aerodyn. 1984;17(3):329–347.
12. K Sangmo, C Haecheon, L Sangsan. Laminar flow past a rotating circular cylinder. Phys Fluids. 1999;11:3312.
13. C Homescu, IM Navon, Z Li. Suppression of vortex shedding for flow around a circular cylinder using optimal control. Internat J Numer Methods Fluids. 2002;38:43–69.
14. Sharul SD, Gregory AK, Robert JM, The suppression of periodic vortex shedding from a rotating circular cylinder. J Wind Eng Ind Aerodyn. 2008;96:1164–1184.
15. Wu J, Shu C. Numerical study of flow characteristics behind a stationary circular cylinder with a flapping plate. Phys Fluids. 2011;23:07360.
16. Strykowski PJ, Sreenivasan KR. On the formation and suppression of vortex ‘shedding’ at low Reynolds numbers. J Fluid Mech. 1990; 218:71–107.
17. Wu J, Shu C, Zhao N. Investigation of flow characteristics around a stationary circular cylinder with an undulatory plate. Eur J Mech B-Fluids. 2014;48:27–39.
18. Sumner D, Richards MD, Akosile OO. Two staggered circular cylinders of equal diameter in cross-flow. Journal of Fluids and Structures. 2005; 20:255–276.
19. Sumner D. Two circular cylinders in cross-flow: A review. Journal of Fluids and Structures.2010;26(6):849–899. 
20.  Zhao M, Lu L. Numerical simulation of flow past two circular cylinders in cruciform arrangement. Journal of Fluid Mechanics. 2018;848:1013–1039.
21. Vedrtnam A, Dheeraj Sagar. Variation of Drag Coefficient, Wall Static Pressure, and Secondary Flow Over a Passenger Car. International Journal of Automotive and Mechanical Engineering. 2018;15(1):5002–5021.
22. Vedrtnam A, Dheeraj Sagar. Experimental and simulation studies on aerodynamic drag reduction over a passenger car. Journal of Fluid mechanics research. 2019;46(1):39–61.
23. Balendra VS Chauhan, Vedrtnam A, Virendra Pratap. Designing Rear View Mirror of Car using CFD and Reverse Engineering. Journal of the Chinese Society of Mechanical Engineers. 2019.
24. Sumner D, Price SJ, Païdoussis MP. Flow-pattern identification for two staggered circular cylinders in cross-flow. J Fluid Mech. 2000;411:263–303.
25. Lam K, Cheung WC. Phenomena of vortex shedding and flow interference of three cylinders in different equilateral arrangements. Journal of Fluid Mechanics. 1988;196:1–26.
26. K Lam, Lo SC. A visualization study of cross-flow around four cylinders in a square configuration. Journal of Fluids and Structures. 1992;6(1):109–131.
27. Igarashi T. Characteristics of the flow around two circular cylinders arranged in tandem (1st report). Bulletin of the JSME. 1981;24(188):323–331.
28. Igarashi T. Characteristics of the flow around two circular cylinders arranged in tandem (2nd report, unique phenomenon at small spacing). Bulletin of the JSME. 1984;27(233):2380–2387.
29. Sumner D. Circular cylinders in cross-flow. Montreal, Canada: 1999.
30. Sumner D, Wong SST, Price SJ, et al. Fluid behaviour of side-by-side circular cylinders in steady cross-flow. J Fluids Struct. 1999;13:309–338.
31. Zdravkovich MM, Paidoussis MP. The Effects of Interference Between Circular Cylinders In Cross flow. Journal of Fluids and Structures. 1987;1:239–261.
32. Meneghini JR, Saltara F, Siqueira CLR, et al. Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangements. Journal of Fluids and Structures. 2001;15(2):327–350.
33. Guo qiang Tang, Chuan qi Chen, Ming Zhao, et al. Numerical simulation of flow past twin near-wall circular cylinders in tandem arrangement at low Reynolds number. Water Science and Engineering. 2015;8(4):315–325.
34. Kyongjun Lee, Kyung-Soo Yang, Dong-Hyeog Yoon. Flow-induced forces on two circular cylinders in proximity. Computers & Fluids. 2009;38(1):111–120.
35. Alam MM, Sakamoto H, Zhou Y. Determination of flow configurations and fluid forces acting on two staggered circular cylinders of equal diameter in cross-flow. J Fluids Struct. 2005;21(4):363–394.
36. Vedrtnam A and Pawar SJ. Experimental and simulation studies on flexural strength of laminated glass using ring-on-ring and three-point bending test. Proc IMechE Part C: J Mechanical Engineering Science. 2017;232(21):3930–394.