In this paper, we will see that the determination of direct bearing angles. As it is known, in bearing angles are often computed used formulas with arctan function. The arctan function gives an angle values between -90^o and +90^o. However, the bearing angle is by definition 0^o to 360^o. Consequently, it is inevitable to examine the process of obtaining the azimuth angle. Classic formulas only work correctly if the edge is in the 1^st quarter. If the edge is located in the other quarters, the angles of the bearing should be examined. In this work we proposed new formulas for direct bearing angles on globe (sphere). Using the formula that we propose will save execution time in codes with intensive geodesic calculations.

Keywords bearing angles, globe, sphere, geographical coordinates, direct bearing angles, classic formulas, arctan function, geodesic calculations, azimuth angle, ellipsoid surface

For example, First Geodetic Basic problem; $P_1({\phi }_1,{\lambda }_1)$ the geographic coordinates of a point P₁ are given in latitude longitude values, S₁₂ the geodetic curve length from point P₁ to point P₂, A₁₂ the bearing angle (azimuth angle) of the length and desired $P_2({\phi }_2,{\lambda }_2)$ the geographic coordinates of a point P₂. The azimuth A₂₁ is desirable which corresponding A₁₂ azimuth angle is because there are approximately 180^o difference between A₁₂ and A₂₁. Thus, the region of A₂₁ is easily predicted. If the two points are on the same meridian or on the same parallel circle the difference between A₁₂ and A₂₁ is exactly 180^o.^1,2

However, in the 2nd Geodetic basic problem; the geographic coordinates latitude and longitude values of the two points are given​​; $P_1({\phi }_1,{\lambda }_1),P_2({\phi }_2,{\lambda }_2)$ and required the geodesic curve length between the two points is S₁₂ and the corresponding azimuths A₁₂ and A₂₁ between the two points. The azimuth calculation is not as easy as in the 1^st geodetic basic problem assignment. If the A₁₂ azimuth is calculated incorrectly, the A₂₁ azimuth will also be incorrect by itself. In this proposed method, formulas are given for how to obtain the azimuth angle directly without any examination. The given method can calculate azimuth without reducing the sphere and ellipsoid surface.

Calculation of between the two points S₁₂ and the corresponding azimuths A₁₂ and A₂₁ from known P₁, P₂ point’s geographical coordinates is also called as geodetic 2^nd basic problem solution (Figure 1). Problem is solved classically with below formulas (Equation 1).^3–5

$\text{σ}=\text{arccos(sin}{\varphi }_{\text{1}}\text{ sin}{\varphi }_{\text{2}}+\text{cos}{\varphi }_{\text{1}}\text{cos}{\varphi }_{\text{2}}\text{ cosΔ}\lambda$

$A_{12}=\arctan \left(\frac{\sin \Delta \lambda }{\tan {\varphi }_2\cos {\varphi }_1-\sin {\varphi }_1\cos \Delta \lambda }\right)$

$A_{21}=\arctan \left(\frac{\sin \Delta \lambda }{\cos \Delta \lambda \sin {\varphi }_2-\cos {\varphi }_2\tan {\varphi }_1}\right)+\pi$

Here $\sigma$ is the angular equivalent of the edge.

If you want to find the metric of the edge:

$S=s/r.R$

$r={180}^o/\pi$

R= radius of the earth

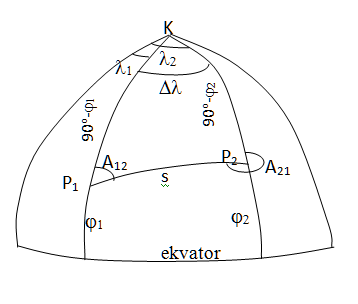
Figure 1 The two points S₁₂ and the corresponding azimuths A₁₂ and A₂₁ from known P₁, P₂ points geographical coordinates is also called as geodetic 2^nd basic problem solution.

It is important to remember that these classic formulas only work correctly if the edge is in the 1st quarter. If the edge is located in the other quarters, the angles of the bearing angle should be examined. For correct angles, the necessary additions should be made according to the Table 1 below.

For direct calculations we give below formulas. In this proposed method, formulas are given for how to obtain the azimuth angle directly without any examination. The proposed method can calculate direct azimuth angles on the sphere and ellipsoid surface, (Equation 2).⁶

Proposed method

$I=\sin \Delta \lambda$

$II=\tan {\varphi }_2\cos {\varphi }_1-\sin {\varphi }_1\cos \Delta \lambda$

${\text{A}}_{\text{12}}=2.\text{arctan}\left(\frac{I}{II-\sqrt{I^2+I{I}^2}}\right)+{180}^o$

$III=\tan {\varphi }_1\cos {\varphi }_2-\sin {\varphi }_2\cos \Delta \lambda$

$A_{21}=2.\arctan \left(\frac{I}{-III+\sqrt{I^2+II{I}^2}}\right)+{180}^o$

To compare direct formula and classical formula results, From the point P₁ to the point P₂ which is located in different quarters each time, the second basic problem solutions were made and the bearing angles calculations were made.

$P_1({\phi }_1,{\lambda }_1)$ , the geographic coordinates of a point P1 are given in latitude longitude values:

${\phi }_1={30}^o, {\lambda }_1={30}^{o }$

$R=6370000m$

Required:$s, A_{12},A_{21}$

If we use the above equations (Equation 1) and (Equation 2) for the solution, for results please see Table 2

In this proposed method, formulas are given for how to obtain the azimuth angle directly without any examination. The given method can calculate azimuth without reducing the sphere and ellipsoid surface. The numerical example that we have given shows the accuracy of the method we propose. The advantage of the method is that no examination is required. In computer calculations, if..end blocks are not used when direct formulas are used. The if..end blocks reduce the execution speed in computer calculations.

For future studies, researchers are advised to try to find more simple direct formulas.

In this proposed method, formulas are given for how to obtain the azimuth angle directly without any examination. The given method can calculate azimuth without reducing the sphere and ellipsoid surface. Using the formula that we propose will save execution time in codes with intensive geodesic calculations

None.

The author declares that there are no conflicts of interest.

None.

1. Grossmann W. Geodata calculations and images in the state survey. Stutgart, Germany: Verlag Konrad Wittwer. 1964.
2. Hristow WK. Die Gauss-Krüger’schen Koordinaten auf dem Ellipsoid. Berlin:Journal Empire Survey Review. 1946;8(61):272–274.
3. Bektas S. Mathematical Geodesy. Turkey: Kamer Publishing House. 2001.
4. Bektaş, S. Jeodezik Hesap-Düzlemde ve Küre Yüzeyinde Jeodezik Hesaplamalar. Samsun:OMÜ publications. 2004.
5. Yaşayan A, Hekimoglu Ş. Spherical trigonometry. Trabzon, Turkey: KTÜ publications. 1982.
6. Bektaş S. Practical Geodesy. Turkey: OMÜ publications. 2016.