The functional information of dissipative systems in Living Matter correlates with both the physical and mathematical regularities defining its material and quantum operational levels. The quantum operational level of Living Matter necessitates employing mathematical models to describe spaces of high dimensions. The physical significance of such an approach helps ascertain the meaning of "action        information" as the "quantum information" of dissipative systems. The quantum properties of dissipative systems determine the competitive balance between the metabolism and homeostasis of  a living organism. The properties of "Quantum information" in dissipative systems exhibit general regularities and can be applied in examining the physical and mathematical principles governing "quantum computers" and materials synthesized based on "quantum dots."

Keywords: dissipative systems, supramolecular systems, functional information, viscoelastic medium, entropy, chaos norm, multidimensional spaces, "action information," second-order phase transition, wave function, cp symmetry, singularity, "unstable stability," qubit, quantum dots, self-oscillatory process, positive feedback, negative feedback, metabolism, homeostasis

Functional information serves as the organizing foundation of Living Matter. It carries the directive for structural alterations in matter. Directed processes of transforming living matter are impossible without such directives.¹ Supramolecular systems act as a unifying bridge between "living" and "non- living" matter.² It is believed that nature employed supramolecular systems to create biological systems.³ Supramolecular systems can recognize each other, move, undergo various transformations while interacting with other molecules, leading to the formation of diverse molecular ensembles (genome, organelles, receptors, membranes, etc.) possessing novel collective functional properties characteristic of biological systems. Self-organization, as a process of coordinated interaction, is characteristic of dissipative systems.⁴ Dissipative systems are open systems with communicative channels to the external environment for exchanging matter, energy, and information. Structural elements of a dissipative system, existing in collective non-local correlation ("entangled state"), combined within a continuous viscoelastic medium, possess a dynamic order structure.

Our accustomed perception of the surrounding reality is based on the three-dimensionality of space. However, numerous physical properties of Matter cannot be explained, let alone described, based on the principles and laws of three-dimensional space. In this regard, there has been a long-standing quest for possibilities and methods of mathematically and physically describing the properties of matter based on higher-dimensional spaces. Multidimensionality is not an objective reality but a form of perception and interpretation of objective reality by our consciousness, used for mathematical and physical descriptions, often revealing new properties and regularities of studied objects and processes. The dimensionality of space determines the potentially possible number of degrees of freedom, defining the dynamic state and behavior of an object. Contemporary physics considers the "physical reality from the perspectives of geometric, field, and relational worldviews, each of which differs in its own interpretation of the properties of space-time and physical interactions."⁵ Only by considering the specific characteristics of interpreting all three worldviews can a sufficiently comprehensive understanding of physical reality and the role of information in the existing world be established. It is precisely from the standpoint of multidimensionality in space that the possibility arises to describe and more fully reveal the nature of the behavior of various fields—both physical (electromagnetic, gravitational, bosonic, fermionic, etc.) and mathematical (scalar, vector, tensor, etc.). A viewpoint grounded in the multidimensionality of space helps explain the physical properties of "time," the duality of matter as "wave-particle," "non-localities," and "information."⁶

The first concept of the world's multidimensionality, four-dimensionality, emerged in the works of H. Minkowski as an additional coordinate to the three dimensions. This fourth coordinate's physical significance is attributed to the concept of "time" and its physical properties. The property of time in the four-dimensional space possesses the directionality of the curvature gradient in space. Depending on the direction and degree of the gradient, it can influence matter and the processes occurring with it. Processes influenced by the fourth coordinate-time can either accelerate or decelerate. Subsequent development in the mathematics of curved surfaces by N. Lobachevsky and B. Riemann allowed for describing and systematizing phenomena in the micro- and macro-worlds based on the properties of five-dimensional spaces. The physical significance of such descriptions defines a new physical reality (a new parameter) of the five-dimensional space as the "action coordinate." The action coordinate of the five-dimensional space, when interacting with a physical object, can convey action information to this object about the directionality of changing its dynamic properties. Initially, the physical significance of the fifth coordinate was considered in the micro-world scales of fundamental particles as a discrete coefficient of energy comparable to Planck's constant.

This fundamental physical constant - Planck's constant, as a unit quantum of action or quantum of quantization energy, can be considered the primary quantum of action information. Simultaneously, the fifth topological coordinate - the "action coordinate" in the macro manifestation of dissipative systems - defines its interaction with an object in the five-dimensional space (dissipative system) and represents a variant of the fermionic field of this space. From a mathematical perspective, action information is a derivative of the moments of impulses of elements constituting the dissipative system and essentially represents the dispersion of the density distribution of these moments of impulses, constituting the density of action information that determines the evolution and behavior of the dissipative system. In this regard, the "fermionic field," as the multi-vector dynamics of the distribution of "action information" density, is sometimes referred to as a "spinor field." However, it's essential to note certain distinctions: the "spinor field" can be either fermionic or bosonic.⁷ This is explained by the fact that spin can be both integral and fractional. Fermions possess fractional spin, while bosons have integral spin. The density of "action information" of dissipative systems emerges during a second-order phase transition and is linked to symmetry breaking (the appearance of anisotropy within the system) and the emergence of high susceptibility (sensitivity) of the dissipative system to weak internal and external regulatory signals. During a second-order phase transition, elements of the dissipative system are in states close to a quantum superposition, i.e., in a non-local correlation state.

According to the theory of "mean field" by Nobel laureate physicist Academician Lev Landau, abrupt second-order phase transitions lead the dynamics of the dissipative system into a commensurable and coordinated state with the field it generates.⁸ Consequently, the dissipative system becomes controllable by an external field. Therefore, an external field could become the controlling parameter capable of adjusting the state.⁹ Another important effect of Landau's "mean field" theory is the deduction that a dissipative system undergoing a second-order phase transition transitions its elements' interaction from short-range to long-range, becoming non-local.^10,11 Quantum states and processes manifest randomness and can only be described based on statistical (probabilistic) mathematical characteristics. One of these characteristics is the wave function, introduced by Erwin Schrödinger - an Austrian theoretical physicist, Nobel laureate in physics, and one of the developers of quantum mechanics and the wave theory of matter.¹² The wave function determines the nature and dynamics of the probabilistic behavior of a quantum particle or system. Properties of quantum information are described by wave functions of fermionic and bosonic fields in multidimensional spaces. For living matter, static states are impossible.¹³ Any processes within living matter, combined into dissipative systems, exist in a self-oscillatory regime and, from a mathematical standpoint, are a strange attractor, which in Riemann's five-dimensional space transforms into a "torus." It is precisely within the mathematical model of a torus that the non-locality properties of dissipative systems are well demonstrated.¹⁴

In an absolute quantum state, matter is unmanifested but possesses maximum information density (quantum information) and exists in a state of maximum quantum coherence. Quantum information ensures an inseparable connection between the material and field states of matter. The transition from an absolute quantum state to a manifested material state occurs at the moment of wave function collapse. Despite dissipating being associated with a form of decoherence, a significant achievement in modern quantum physics has been the discovery of the opposite, constructive role of dissipation in generating entangled states.¹⁵ Different interpretations exist regarding the peculiarities of the meaning of the wave function. Professor of Applied Mathematics at Växjö University, Sweden, and Director of the International Center for Mathematical Modeling in Physics and Cognitive Sciences A. Yu. Khrennikov notes that one physical interpretation of the wave function is the "density of interference of probabilities." Quite recently, interference of probabilities was obtained within classical probability theory, showing the importance of the quantum system's interaction with various conditions of the external environment.¹⁶

In 1927, Niels Bohr proposed using the "Complementarity Principle" to describe the properties of matter, stating that for a more complete description of matter, both its wave and particle characteristics should be considered. Essentially, Bohr's "Complementarity Principle" defines Matter as "Substance and Field," considering their quantum properties.¹⁷

One of the widely known fundamental particles with wave properties is the photon. The photon, as a quantum of the electromagnetic field (specifically, a quantum of light), acts as a carrier of electromagnetic interaction and information. The relationship between the field and charge is defined by Maxwell's equations in classical electromagnetic theory. Hence, fundamental laws of symmetry (laws of invariance), which define the physical properties and mathematical interconnection of basic physical quantities - charge, energy, momentum, angular momentum - with space and time, can be transposed to operations involving electromagnetic waves (photons). One such law, CP symmetry (combined parity law), reflects the dynamic complex-conjugate interaction of numerous phenomena functioning within matter at different hierarchical levels. The CP symmetry law corresponds simultaneously to charge and spatial inversion. The CP symmetry indicates a generalized principle of conjugating the "material" and "quantum" within living Matter, as a necessary condition for its dynamic balance in a state of "unstable stability," corresponding to the principle of existence of living dissipative systems. The formation and storage of biological information, functional information, are fully related to the CP symmetry law. In this context, the principle of "mathematical singularity" of CP symmetry relates to the concept of "biological singularity."¹⁸

Singularity is a special point at which singleness of existence, events, or phenomena can simultaneously manifest or vanish. Mathematical singularity (peculiarity) is a point where a mathematical function tends toward infinity or exhibits some other irregular behavior. Biological singularity is connected to the biological evolution and mathematical singularity of living Matter.¹⁹ Ancient philosophers in their intuitive models unified the principle of "unstable stability" around the point of singularity, correlating it with the concept and properties of the "Great Limit," wherein singleness of existence, events, or phenomena arises (Figure 1). Based on these properties of CP symmetry, Academician Lev Landau proposed in 1957 that CP symmetry should be considered as the true symmetry between matter and antimatter, capable of leading to particle annihilation.⁹ The structural-functional manifestation of the "Great Limit" in conjunction with the fundamental laws of symmetry can be demonstrated through a model of a cube where complex-conjugate functions of various spatial-functional (structural-functional) interactions are located at its vertices. The intersection of the inner diagonals of the cube spatially defines the "Great Limit" as the boundary transition between material and quantum states and illustrates the principle of superposition between these states. In Figure 2, marked with the number "1." The unitary essence of the "Great Limit" arises from the mathematical operation "composition":

eibx ◦ e -ibx = 1

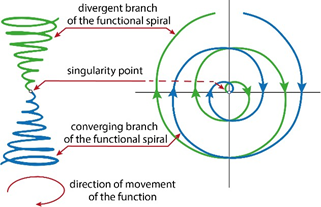
Figure 1 Dynamic state of the "Great Limit" as a model of "unstable stability" around the "point of singularity."

Figure 2 Model of a cube with complex-conjugate functions at its vertices.

This formula combines the interaction of complex-conjugate functions, which can be interpreted as spirals with opposite twisting directions (Figure 1). From a physical standpoint, such a model corresponds to the interaction of opposite charges or electromagnetic waves with right and left polarizations. Displacement of the function from the "Great Limit" leads to symmetry breaking, the emergence of imbalance, and anisotropy in the environment. The distinguished scientist V.I. Vernadsky stated that "Only the non-equilibrium state of 'leftness' and 'rightness' in the biosphere ensured the emergence of life on planet Earth."²⁰ Another renowned scientist, the French physicist Pierre Curie, noted that "dissymmetry generates action; if there is no dissymmetry, then the phenomenon is impossible."²¹ Quite recently, the scientific team of astronomers from the Sloan Digital Sky Survey (SDSS) under the leadership of Michael Longo (USA) demonstrated through years of research that the current state of the Universe is both non-equilibrium and integratively right-handed.²² Consequently, it is evident that life on Earth integratively evolved as right-handed.

Living matter is known to possess relative chiral purity in its constituting biopolymers. Proteins and their derivatives predominantly contain "left-handed" amino acids (L-amino acids), while nucleic acids (DNA and RNA) contain only "right-handed" sugars (D-sugars). The polarization of our cell's cytoskeleton is right-handed, and the cumulative polarization of the whole organism is also right- handed.²³ The functioning basis of Dissipative systems in living organisms is also right-handed asymmetry. One of the fundamental fields, the electromagnetic field, governs interacting processes in living matter. Hence, many physiological processes may be regulated by flows of electromagnetic radiation of right polarization. Prolonged exposure to left-polarized flows may lead to changes or even disruption of natural physiological processes. In 2012, at the Nizhny Novgorod State Medical Academy in the laboratory of the Department of Physiology, research was conducted on the proliferative capacity (cell division) of human liver cell line cultures of both normal and neoplastic lines and rat glial cells under the influence of fields of right and left polarization. The study results showed that the field of right polarization significantly suppressed the metabolism and proliferation of neoplastic cell lines.²⁴ The field of left polarization activated metabolism and accelerated the proliferation of neoplastic cell lines. Conversely, the field of left polarization slightly reduced the activity of metabolism and proliferation of normal cell lines. On the contrary, the field of right polarization gently stimulated the metabolism and proliferation of normal cell lines.²⁵

The concept of information in the scientific realm has undergone revolutionary changes. Modern methods of information processing in quantum computers, as well as in dissipative systems, are based on the laws and properties of fundamental symmetries. The fundamental notion in classical information theory is the "bit," which takes values of 0 or 1. The paradigm shift in our understanding of information began with replacing the classical "bit" with its quantum analog - the "qubit." Photons, serving as the foundation of qubits in quantum computers, carry information about the direction of its propagation (Poynting vector) and polarization (axial vector) (Figure 3).²⁶ A qubit comprises 8 cubits. Cubits within the qubit can exist in an equilibrium (metastable) state, where information is absent, analogous to the state of the "Great Limit." Altering the equilibrium state of the cubits results in the emergence of information, described in the qubit by a vector. This vector is the outcome of the interaction between polar and axial vectors, describing the direction of information propagation and polarization in space. Any non-equilibrium state of the qubit contains "action information." Quantum computers essentially operate with the properties of information in a five-dimensional space, possessing additional degrees of freedom. The information density of a qubit significantly surpasses that of a bit. Photons in quantum computers, existing in a state of superposition (quantum non-locality), represent a quantum dissipative system. In 2022, the Nobel Prize in Physics was awarded to scientists Alain Aspect (Palaiseau, France), John F. Clauser (California, USA), and Anton Zeilinger (Austria) for experiments with entangled photons, establishing the violation of Bell inequalities, and for their contributions to quantum informatics (Figure 4).²⁷

Figure 3 Model of a qubit with embedded cubits.

Figure 4 "Bloch Sphere" as a qubit model.

The described qubit model by mathematicians and programmers is transposed into its simplified model, the "Bloch Sphere," which considers the states of polar and axial vectors, defining the wave function ψ of the qubit. It's worth noting that it's impossible to fixate any intermediate position of the wave function due to quantum laws: any measurements will only yield 0 or 1, and determining the relationship of complex coefficients will only be possible through numerous repetitions and probability calculations. Another equally interesting example of quantum dissipative systems is "quantum dots." In 2023, the Nobel Prize in Chemistry was awarded to scientists Mungi Bawendi (Massachusetts Institute of Technology), Louis Brus (Columbia University), and Alexei Ekimov (Nanocrystals Technology Inc) from the USA for the development and synthesis of "quantum dots." Devices utilizing materials with "quantum dot" properties allow obtaining emissions across a vast range of discrete pure colors within the optical spectrum.²⁸ Despite the Nobel Prize being awarded in the field of chemistry for the development and synthesis of materials with "quantum dot" properties, the "quantum dots" themselves, as objects of study, are closely related to physics. The physical principle of an optoelectronic crystal, consisting of "primary cells" - "quantum dots," can be associated with the complex-conjugate functions of the "Great Limit," described earlier, which, on an energetic level, enables the control of the crystal's operation.

Systems exhibiting "unstable stability" properties can be associated with dissipative systems functioning far from the point of thermodynamic equilibrium. The state of functional systems under "unstable stability" from a mathematical perspective can be characterized as an auto-oscillatory process with trajectories of a strange attractor or a torus. An essential characteristic of auto-oscillatory processes is the presence of negative feedback (NFB).²⁹ Quantum dots, as a particular state of the optoelectronic state of matter, are characterized by the fact that their operation is only possible under a non-equilibrium initial state of the valence layer of semiconductor crystal atoms, which can be correlated with the complex-conjugate functions of the "Great Limit," ensuring high sensitivity to external control signals, leading to emission within a narrow, specific range. It's important to note that the existence of "quantum dots" of matter (where the quantum-material state of matter is realized) might not be possible in all types of materials. They can be obtained under one crucial condition: the "primary cell" forming the quantum dot must possess one critical property: the atoms constituting the material of this primary cell should form a complex-conjugate structure, the generalized valence band of which contains 8 electron clouds, corresponding to the maximal filling of the energy levels of this cell. It is precisely this combination of chemical elements of the "quantum dot" that ensures a metastable (unstable stability) state of electron clouds, capable of reacting to an external control signal and transitioning to a higher energy level of the "conduction band," surpassing the "forbidden zone."³⁰

At the moment of the electron's return to the initial state in the "valence band," narrow-band radiation of monochromatic light quanta occurs. An electron that transitions to the conduction band retains a superposition state with electron clouds of the "valence band" of the quantum dot. A single cell of a quantum dot containing 8 electron clouds can be compared to the property of the "Great Limit" cube, where the equilibrium state of the cube's diagonals at point "1" represents the true "Great Limit" formed by the equilibrium state of the 8 cubits of this cube. The existence of 8 interaction combinations is a systemic condition for building and stable functioning of non-equilibrium systems both in inanimate and living Matter. Such a state allows, with the presence of a correctly selected external control parameter (factor), the control (regulation) of processes in Matter, maintaining it in this non-equilibrium auto-oscillatory state according to the NFB principle. Fluctuations and Self-Oscillations via NFB as a Necessary Condition for Self-Organization in Open Dynamic Systems to Maintain their Dynamic Stability. The excitation of self-oscillations (the emergence of autogeneration) will always be accompanied by a decrease in the total entropy of the system, i.e., a reduction in dynamic chaos and the maintenance of the necessary level of order in the system. An auto-oscillatory process in the dissipative system of a living organism provides conditions for maintaining homeostasis.³¹

Homeostasis is an integrative dynamic process regulating the functional and morphological (morphofunctional) relative internal constancy of a living organism.³² Tissue homeostasis ensures the preservation of the relative stability of the total number of cells, an optimal ratio between dividing cells, differentiated, and apoptotic (undergoing apoptosis) cells within the tissue composition. In the processes of homeostasis and metabolism, feedback loops play a significant role. Norbert Wiener, one of the founders of cybernetics and artificial intelligence theory, considered the feedback principle as the "mystery of life," assigning it a fundamental role in studying phenomena in the living nature.³³ For the creation of new structures, new organs in the process of organism growth and development, positive feedback (PFB) is necessary, destabilizing the system (bringing this system to a new level of structural organization). For maintaining a stable state, negative feedback (NFB) is necessary.³⁴ The balance of PFB and NFB relationships provides the ability of living organisms both to grow and self-regulate individual organisms and, ultimately, self-preservation and species stability. The formation of dissipative structures involves positive feedback (PFB) and forms the basis of tissue differentiation in morphogenesis. The preservation of the auto-oscillatory regime in a dissipative structure occurs with the involvement of negative feedback (NFB).³⁵

Maintenance of homeostasis is only possible with NFB, which actually regulates homeostasis, and PFB, which creates the necessary and sufficient number of interacting elements of the system and the necessary-sufficient structure of order between these system elements. Homeostasis, essentially, is an auto-oscillatory process with NFB of informational regulation (dissipative regulation), maintaining the constancy of vital structural characteristics of living matter, the entire living organism.³⁵ Normal homeostasis, as a health criterion, is related to relative order - the "norm of chaos" of structural elements of the dissipative system.³⁶ Both high entropy (excessive chaos) and minimal entropy striving towards zero (complete phase coherence) lead to the loss of functional information in living matter and, consequently, the loss of its normal physiological functioning.³⁷ The value of the "norm of chaos" (entropy norm) is a systemic criterion of human "health norm." There is a constant competition between two types of feedback - PFB and NFB. The spatial-temporal dynamics of a dissipative system's state, associated with its degree of chaos, is the result of the competition between these two types of feedback. Positive feedback (PFB) determines the growth, formation, and emergence of a dissipative system by ensuring a sufficient and necessary number of elements of this system. The formed dissipative system possesses several energetic characteristics: temperature, pressure, Gibbs energy.. However, for example, in the nervous system, excessive positive feedback causes an increase in the reaction, which may underlie the development of diseases. Negative feedback, on the contrary, reduces the activity of CNS neurons and the response, which underlies self-regulation (adaptation). If the balance of feedback is disturbed, the PIC brings the functioning of the dissipative nervous system into a new functional (morphofunctional) state, which usually leads to pathological homeostasis and even possible destruction (death) of the functioning dissipative system.³⁸

The formed new state of the system occurs simultaneously with the involvement of all its constituent components.³⁹ Such a new state of the system carries a new regulatory (informational) signal, complementarily significant already for other levels of cascade interaction and regulation. Moreover, the dissipative nature of the regulatory signal is formed and uniformly—essentially non-locally— perceived by all elements of the dissipative system with minimal external influences on it. At the same time, the viscoelastic medium of the dissipative system performs the function of a "receiver," a converter capable of maintaining or changing the informational density of the regulatory signal, and an "amplifier."⁴⁰ The properties of viscoelastic interaction between the elements of the dissipative system through its viscoelastic medium provide a non-local, essentially quantum character of Living Matter's behavior.

The dissipative systems of a living organism are the connecting link between the material and quantum states of the processes occurring in Living Matter. The quantum properties of dissipative systems of living matter indicate the need to perceive the multidimensionality of the space of the surrounding world, which opens to our understanding its special physical properties.

This work is carried out as part of a private scientific development of the authors under the guidance of Dr. Igor Orzhelskyi, CME Swiss AG, Switzerland.

The authors declare that there is no conflict of interest.

None.

1. Orzhelskyi LV, Kuznetsov AN. Theoretical foundations of physico-mathematical medicine; 2016. pp 54.
2. Konovalov AL. Supramolecular systems: a bridge between inanimate and living matter. Russ Chem Bull. 2011;60:1–10.
3. Lehn JM. Supramolecular chemistry: concepts and perspectives; 1998. 334 p.
4. Haken G. Information and self-organization: a macroscopic approach to complex systems; 2006. 248 p.
5. Vladimirov YS. Metaphysics. Moscow: BINOM, Laboratory of knowledge; 2002.
6. Immanuel K. Critique of pure reason. 1994. 591 p.
7. Zhurzhin AN. Quantum theory of lorentzian fermionic differential forms. Theor Math Phys. 2020;202(2):207–242.
8. Landau LD, Lifshitz EM. Statistical physics. Part 1. 4th edition. Moscow: Nauka; 1995.
9. Landau LD, Lifshitz EM. Quantum mechanics: non-relativistic theory. 6th revised edition. Moscow: Fizmatlit; 2004. 800 p.
10. Yu L. Klimontovich. Statistical theory of open systems. Volume II; 2019. 438 p.
11. Yu L. Klimontovich. Kinetic theory of non-idessal gas and non-ideal plasma. Science. 1975. 352 p.
12. Erwin S. What is life? and other scientific essays; 1944.                                                            
13. Prigogine I, Nicolis G. Biological order, structure, and instabilities. Q Rev Biophys. 1971;4(2):107–148.
14. Albert Goldbeter. Dissipative structures in biological systems: bistability, oscillations, spatial patterns, and waves. Philos Trans A Math Phys Eng Sci. 2018;376(2124):20170376.
15. Korotayev SM, Morozov AN. Non-locality of dissipative processes - causality and time. Moscow: Fizmatlit; 2018. 216 p.
16. Yu A. Khrennikov. Introduction to quantum information theory. Moscow: Fizmatlit; 2008. 284 p.
17. Pais A. Niels Bohr’s Times, in Physics, Philosophy, and Polity. 1991. In: Held C Oxford.  
18. Zeh, Heinz-Dieter. The Physical basis of the direction of time. 4th edition.
19. Weizsäcker CC. von: Order and chaos in economics. In: Gerock W, Haken H et al. editors. Order and Chaos in inanimate and living nature. Stuttgart; 1989.
20. Vernadsky VI. Philosophical thoughts of a naturalist. Moscow: Nauka; 1988. 520 p.
21. Pierre Curie. Selected Works. Moscow-Leningrad: Izd. Science; 1966.
22. SDSS Collaboration. The thirteenth data release of the sloan digital sky survey: first spectroscopic data from the SDSS-iv survey mapping nearby galaxies at apache point observatory (English).
23. Morphogenesis in individual and historical development: symmetry and asymmetry. Collected Works. In: Rozhnov SV. Series "Geo-biological Processes in the Past". Moscow; 2013. 330 p.
24. Stepanenko VD, Stepanenko KV, Kuznetsov AN. Patent No. 2491970 RF, "Method for correction of directionality and dynamics of biophysical processes of biological objects", 10.09.2013
25. Stepanenko VD, Stepanenko KV, Kuznetsov AN. Patent No. 2491971 RF, "Method of controlled exposure to biological object by electromagnetic radiation of a semiconductor injection generator (Variants)". 10.09.2013
26. Shuo Sun, Hyochul Kim, Zhouchen Luo, et al. A single-photon switch and transistor enabled by a solid-state quantum memory. Science. 2018;361(6397):57–60.
27. Alain A, John C, Anton Z. The Nobel Prize in Physics 2022 «for experiments with entangled photons, establishing the violation of Bell inequalities and pioneering quantum information science».
28. Moungi G. Bawendi, Louis E. et al. The Nobel Prize in Chemistry 2023 "for the discovery and synthesis of quantum dots"
29. Fedotkin IM, Orzhelskyi IV. General theory of effects in processes of heat, mass, energy, and information transfer. Kyiv; 2002. 288 p. - (Series: New Physical Effects, Their Use, and Perspectives; Book 1, Part 1).
30. Fedotkin IM, Orzhelskyi IV. General theory of effects in processes of heat, mass, energy, and information transfer. Kyiv; 2002. 238 p. - (Series: New Physical Effects, Their Use, and Perspectives; Book 1, Part 2).
31. Kotolyupov VA, Levchenko VF. Multifunctionality and homeostasis. Regularities of the organism's functioning important for maintaining homeostasis. Zh Evol Biokhim Fiziol. 2009;45(4):449–451.
32. Bekhtereva NP. The magic of the brain and the mazes of life. AST publishing; 2015. 384 p.
33. Norbert W. Cybernetics: or control and communication in the animal and the machine. 2nd ed. 1961. Cambridge: The MIT Press. Fourth Printing; 1985.
34. Positive and negative feedback loops in biology. The Albert team; 2022.
35. Igor O, Andrey K, Elena VD. Dissipative regulation: a new approach to understanding the regulatory mechanisms in the human body. Clinical Immunology & Research. 2020;4(1):1–4.
36. Natalia J. Nonlinear dynamics of biological systems. Contemporary Physics. 2012;53(2):137–168.
37. Carlo DL, Paola R, Sabino I, et al. On collective molecular dynamics in biological systems: a review of our experimental observations and theoretical modeling. Int J Mol Sci. 2022;23(9):5145.
38. Géza Ó, Gustavo D, Jeffrey K. Differences in the critical dynamics underlying the human and fruit-fly connectome. Phys Rev Research; 2022.
39. Brian G, Antony MD. The structural basis of molecular adaptation. Mol Biol Evol. 1998;15(4):355–369.
40. Heine H. The extracellular matrix and ground regulation: basis for a holistic biological medicine. North Atlantic Books; 2007.