In this paper the author emphasizes on the basic principle of Modulated Temperature Differential Scanning Calorimetry (MTDSC), advantages of MTDSC compared to conventional DSC, calculation of heat flow components and heat capacity components, factors effecting the MTDSC signals and application of MTDSC in drug development. MTDSC a sinusoidal modulation is overlaid on a conventional linear heating ramp, in which the sample temperature increases continuously with time. The linear heating rate gives the information same as the standard DSC, while the sinusoidal heating rate determines the fraction of the total heat flow corresponding to the changing heat rate. The total heat flow rate depends on heat capacity and change in heat capacity. This fraction of heat flow is called Reversing heat flow or the heat capacity component of the Total heat flow. The kinetic component is time dependent, also known as Non-reversing heat flow that does not respond to the changing heating rate. For accurate measurements of heat flow components and heat capacity components optimized experimental parameters must be chosen. MTDSC in particularly plays an preformulation studies to establish Tg, polymorphic forms, polymorphic transitions, ensure stability by drug excipient compatability studies and to determine enthalpy of polymorphic transitions.

Keywords: MTDSC, heat flow component, heat capacity component, MTDSC signals, reversing and non-reversing signals

MTDSC, modulated temperature differential scanning calorimetry; DSC, differential scanning calorimetry; PET, polyethylene terephthalate; PC, polycarbonate

Differential Scanning Calorimetry (DSC) is a thermal technique employed to study the behavior of a crystalline or amorphous substance under the influence of varying temperature as a function of time. DSC is applicable to both solids and liquids and provides both quantitative and qualitative information regarding the transitions in materials involving exothermic and endothermic processes and changes in heat capacity. Modulated Temperature Differential Scanning Calorimetry (MTDSC) is an extension of DSC to which sinusoidal wave modulation of temperature program is applied i.e. the technique measures the difference in heat flow between a sample and reference as a function of time and temperature.¹ By modulating the temperature program both quality and quantity of information obtained compared to conventional DSC are improved. To be more specific in MTDSC a sinusoidal modulation is overlaid on a conventional linear heating ramp, in which the sample temperature increases continuously with time.

In conventional DSC in a typical linear heating program, where both physical and chemical reactions are absent the heat flow signal is dictated by heat capacity. But when a kinetically controlled chemical event occurs the resultant heat flow signal in conventional DSC is a single peak representing a combination of heat flow associated with both heat capacity and that of the chemical event, where the heat flow due to heat capacity is reversible and that due to chemical event is irreversible. Whereas MTDSC separates these two processes,^2‒4 based on their difference in response to the underlying modulated temperature programs. MTDSC imposes complex heating profile on the sample which is equivalent to two experiments run simultaneously on the material- one at linear heating rate and the other at sinusoidal heating rate.

MTDSC can be easily understood by comparing with the standard DSC. The schematic diagram of a typical heat flux DSC cell as shown in Figure 1 shows a sample pan and a reference pan on raised constantan disk platforms. Differential heat flows through the sample and reference when heat is transferred through the disk, and measured by a thermocouple of constantan disk and chromel wafers below the platforms, which directly measures the sample temperature. The thermocouple is made of chromel and alumel wires attached to chromel wafers.⁵ Through an orifice in the heating block, midway between the raised platforms, purge gas is introduced into the sample chamber, to ensure uniform and stable thermal environment for excellent baseline flatness and exceptional sensitivity. In DSC, the linear heating or cooling rates are as fast as 200^ºC/min to as slow as 0^ºC/minute (isothermal conditions).⁶

Figure 1 Schematic diagram of heat flux DSC cell.

Hence in a nut shell, MTDSC applies two simultaneous heating rates to the sample. The linear heating rate gives the information same as the standard DSC, while the sinusoidal heating rate determines the fraction of the total heat flow corresponding to the changing heat rate. The total heat flow rate depends on heat capacity and change in heat capacity. This fraction of heat flow is called Reversing heat flow or the heat capacity component of the Total heat flow. The kinetic component is time dependent, also known as Non-reversing heat flow that does not respond to the changing heating rate. Non-reversing heat flow is determined by subtracting the reversing heat flow signal from the total heat flow signal. MTDSC doesn’t measure reversibility or non-reversibility of transitions. The term Reversing denotes the true heat capacity i.e. the heat associated with increasing or decreasing materials temperature is reversible, while non-reversing denotes the reversing signal associated with heat capacity change, which may or may not be reversible.

Moreover, it is not easy to identify the nature of transitions that occur in single component and multicomponent systems. Examples include an enthalpic relaxation peak when superimposed by heat capacity variation at glass transition temperature is large enough to be misinterpreted as melting transition. In such cases, to increase the sensitivity either mass or scan rate are to increased but resolution of the data is compromised. Also, the detection of weak signals is strongly influenced by baseline curvature and stability. Baseline might not always be linear depending on various factors such as moisture evaporation from the sample, differences in thermal contact between the sample and the DSC pans and overall baseline characteristics of the specific DSC cell.

Figure 2 & Figure 3 compares the DSC and MTDSC curves of quench cooled polyethylene terephthalate (PET) from a temperature above its melting point respectively. In Figure 2 the resulting heat flow signal is plotted in milliwatts (mJ/sec) versus temperature or time. Single heating rate produces single heat flow rate signal, which is a sum of all heat flows occurring at any point in temperature or time.⁷ Figure 3 shows the MTDSC temperature profile, which includes linear temperature and modulated temperature change curve. The total heat flow signal (green) is the same as that of the standard DSC; the reversing signal (blue) gives the heat capacity and melting of the sample, whereas the non-reversing (brown) signals gives the kinetic processes of enthalpy recovery at Tg, cold crystallization, and crystal perfection.

Figure 2 DSC signal for PET.

Figure 3 MTDSC signal for PET.

To better understand the effect of change in temperature on heat flow rate a plot of time vs derivative of temperature is studied which gives the modulated heating rate. Figure 4 shows the sinusoidal change in temperature in MTDSC. As a result, the heating flow also changes sinusoidally. The important point to be noted is that the heating rate for MTDSC is never negative (no cooling). Figure 5 represents the Modulated heat flow and modulated heating rate, which the measured signals from MTDSC. All the other MTDSC signals are calculated from these two measured signals.^1,8

Due to the modulation of temperature, MTDSC is sometimes incorrectly interpreted as heat-cool technique, where in fact sinusoidal modulation of temperature is employed with heating rate always being positive. In MTDSC, we can choose either heat-cool or only heat (isothermal) conditions as required by the analysis.

Figure 4 Modulated Heating Rate.

Figure 5 Modulated Heat Flow and Modulated Heating Rate.

In Figure 6 the modulated temperature increases and decreases while the average temperature increases constantly. Time based derivative of the signal shows an average heating rate of 1.0^ºC/min, and heating rates modulates as -1.0 to 3.0^ºC/min. These temperature modulation conditions provide heating and cooling, suitable for the measurement of heat capacity and its changes. Whereas in Figure 7 temperature modulates from 0 to 4.0^ºC/min with an average heating rate of 2^ºC /min, representing heat-iso conditions since the heating rate goes to zero with no cooling. Heat-iso conditions are useful for the measurement of initial crystallinity in semi-crystalline polymers.

Figure 6 Temperature Modulation from -1 to 3.00C/min

Figure 7 Temperature Modulation from 0 to 4.00C/min.

The relation of heat flow and heat capacity signals of MTDSC is given by,¹

$\frac{dH}{dt}=C_p\frac{dT}{dt}+f\left(T,t\right)$

Where

dH/dt is total heat flow rate (mW, or mJ/s)

C_p is heat capacity of the sample,

dT/dt is heating rate (^ºC/min)

f (T,t) is heat flow which is a function of time and temperature.

The above equation reveals that the total heat flow has two components, one a function of applied heating rate while the other is a function of time at an absolute temperature. The other signals are given by

$$Totalheatflow= \frac{dH}{dt},thesumofalltheheatflow$$

$$Reversingheatflow=C_p\frac{dT}{dt} alsoknownasHeatcapacitycomponent$$

$$Non-reversingheatflow= f\left(T,t\right)alsoknownasKineticcomponent$$

Calculation of MTDSC signals

All the three signals are shown in Figure 2 on a sample of quench cooled PET.^9–12

1. The total heat flow is the average value of the measured modulated heat flow signal as seen in Figure 4. It involves the use of Fourier transform analysis on the sine wave, which calculates the average continuously rather than the simple average which significantly limits the resolution.
2. The reversing heat flow is composed form reversing heat capacity signal which is given by

$Rev C_p=\frac{Heat Flow Amplitude}{Heating Rate Amplitude}\times K{C}_{p }Rev$

Where

KC_p Rev = Calibration Constant for Reversing C_p.

Rev Heat Flow = Rev C_p x Average Heating Rate.

3. The non-reversing heat flow is composed by subtracting the reversing heat flow signal from the total heat flow signal.

Similarly, the heat capacity components are given by

$$\text{Total heat capacity }=\frac{Total Heat Flow }{Average Heating Rate}\times K{C}_{p }Total$$

$\text{Reversing heat capacity }=\frac{Heat Flow Amplitude}{Heating Rate Amplitude}\times K{C}_{p }Rev$

$\text{Nonreversing heat capacity }=Total heat capacity-Reversing heat capacity$

In MTDSC sinusoidal modulation of temperature varies between a minimum and a maximum value wherein the heating rates depends on underlying heating rate (0-10^ºC/min), period of modulation (10-100 seconds) and amplitude of temperature modulation (±0.01-10^ºC). Hence the minimum modulated heating rate is positive, zero or negative.

The modulated temperature program,¹³ is given by

$$T\left(t\right)=T_0+qt+A_{T}sin(\phi t)$$

Where T₀ = initial temperature

q = linear heating rate

A_T = oscillation amplitude

The theory of MTDSC and the interpretation of data depend on the following

1. Use of small, thin and hermetically sealed sample minimizes temperature gradient and maximizes conductivity during heating and cooling cycles.
2. A device which responds instantaneously to heat flow with no lag time is used.
3. The heat flow due to heat capacity in heating and cooling cycles is completely reversible with no hysteresis.

Advantages of MTDSC

1. Advantages of MTDSC are but not limited to the separation of the overlapping phenomenon and deconvolution of complex transitions, greater resolution without loss of sensitivity, identifying metastable state and ease of determining heat capacity.
2. The overlapping processes can be distinguished with MTDSC as they split into reversing and non-reversing heat flow. Processes such as enthalpic relaxation, crystallization, evaporation, decomposition, and cure are non-reversing heat flow. Melting can occur both as reversing and non-reversing heat flow, however the fraction of melting in both the situations depends on the experimental conditions.
3. Improved sensitivity in detecting weak transitions.
4. Improved sensitivity and resolution can be obtained within a single experiment.
5. More accurate measurement of polymer initial crystallinity.
6. Direct measurement of heat capacity.
7. Quasi-isothermal measurement of heat capacity changes during reactions or kinetic processes.

Factors influencing MTDSC

The key to obtain accurate and reproducible results in MTDSC or in conventional DSC mainly depends on the factor that the sample under study must be able to follow the heating profile it is subjected to. Factors that influence MTDSC data are mainly poorly chosen experimental parameters such as sample size, heating rate, distortion of modulation of temperature, temperature amplitude of modulation, inaccurate heat capacity measurements, factors affecting deconvolution procedure and influence of pan type.

Sample size

Not too little sample or large amounts of sample are to be used. Too little sample provides inadequate temperature profile where as too large amount of sample causes low heat capacity readings. Optimized sample size would be 10-20mg which are flat and thin, however depends on pan size too. Contact between sample material and DSC pan is optimized by crimping.^11,14

Heating rate

Low ramp rates or slower heating rates are preferred to allow sufficient modulations during the temperature modulation. A 1-5^ºC/min ramp rate is desirable however a minimum of 4-5 modulations are required to be run before selecting the appropriate ramp rate.

To obtain the best possible results from MTDSC, select optimum values for average and modulated heating rates. The average heating rate is selected first, and then temperature modulation, period and amplitude, which defines the modulated heating rate. Parameters are selected in such a way that

1. The modulation period is long enough to allow enough time for heat to flow between the sensor and the sample.
2. The modulation amplitude is sufficient to have good sensitivity but not too large to reduce resolution.
3. The average heating rate is slow enough to provide good number of modulation cycles during the transition period.

Distortion of modulation

When the maximum and minimum modulating heating rates are beyond the capacity of the instrument, sinusoidal temperature parameter is distorted. This can be assessed by using 10.079mg of aluminum oxide for periods ranging from 10 to 80sec. It was found that the distortion is pronounced at low temperatures and for short periods.¹⁴

Temperature modulation period

It is defined as the time in second’s required completing one modulation cycle. It depends on the sample size, sample thickness, sample conductivity, sample pan, and type of measurement being made. Optimizing the modulation period is important, as too long period’s leads to reduction in average heating rate and hence an increase in the length of the experiment, and too little intervals leads to improper measurement of heat flow between sample and sensor.¹⁴ Too little periods reduce heat flow amplitude, resulting in reduced reversing heat capacity and reversing heat flow signals.

$Rev C_p=\frac{Heat Flow Amplitude}{Heating Rate Amplitude}\times K{C}_{p }Rev$

Temperature amplitude of modulation

The temperature modulation amplitude is the sinusoidal change in temperature superimposed on the average change.^4,14 As instantaneous heating rate is directly proportional to amplitude, the larger the amplitude the larger the heat flow response. Amplitude of ±0.5 to 2^ºC is preferable. Amplitudes less than ±0.1^ºC gives poor sensitivity while amplitudes greater than ±2.0^ºC causes decreased resolution.

$\frac{dT}{dt}= ß+A_T\omega \text{cos}\left(\omega t\right)$

Where:

dT/dt = instantaneous heating rate (^ºC/minute)

ß = underlying heating rate (^ºC/minute)

AT = modulation amplitude (^ºC)

ω = angular frequency = 2p/modulation period (min^-1)

t = time (minutes)

Large amplitudes give larger changes in heating rate, though increases sensitivity also has a risk leading to a situation where the material cannot follow modulation.

Measurement of heat capacity

Conventional DSC requires three scans, while MTDSC requires single sample run with suitable heat capacity calibration. Measurements of heat capacity with MTDSC have been discussed earlier in this paper. Direct heat capacity measurements are made by running the sample in the same conditions as for heat capacity calibration constant.

Factors such as cell purge gas, sample mass, period and pan mass influence heat capacity measurements.¹⁴

Cell purge gas

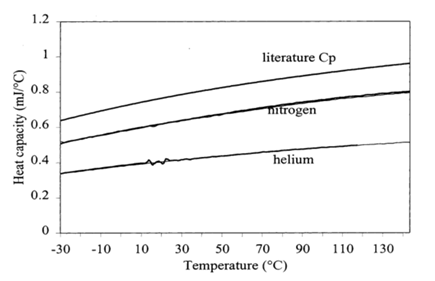
An inert gas such as nitrogen or helium is passed through DSC cell to create an inert environment, and to prevent contamination of the constantan disk (Figure 8). The picture depicts the fact that at higher temperatures the use of nitrogen purge results in uncalibrated values similar to that of the literature. It was supposed that the high thermal conductivity of helium gas conducted the heat away from the sample leading to temperature gradient in the cell leading to low heat capacity measurements due to lack of temperature modulation throughout the sample. Purge gas effect could be eliminated by calibrating the cell with the same purge gas. Though helium purge gas results in low heat capacity measurements it has its own advantage of shorter periods of temperature modulation without distortion.

Figure 8 Uncalibrated heat capacity measurement for aluminium oxide with nitrogen and helium cell purges.

Sample mass

The effect of sample mass is explained by taking into account the thermal gradient that builds up due to large samples, where not all sample follows the same temperature modulation. The heat capacity due to a small fraction of large sample taken is accountable to heat capacity measurement.

Period

As the temperature modulation period decreases, the thermal lags that develops in the larger sample mass leading to lowering of measured heat capacity (Figure 9). Boller et al.⁴ analysed two aluminium samples weighing 13.580mg and 40.127mg at 2^ºC/min heating rate for 20, 30, 40, 50, 60, 70 and 80 seconds with the amplitude of the derivative modulated temperature constant. As the instrument sensitivity depends on amplitude it is kept constant throughout the study. The authors have observed that the decreased period reduces the heat capacity attributing the change to thermal gradient built up across the sample. The same results were obtained when the analysis was performed with indium by Cao et al.¹⁵

Figure 9 Effect of period on the measured specific heat capacity.

Pan mass

The heat capacity measured in MTDSC depends on the difference in mass between the sample and reference pans, which is more significant for small samples. The sample and the reference pans measure zero heat capacity if they weigh exactly the same. And then when the sample is added, the measured heat capacity corresponds to the sample itself. Difference in pan mass of around ±0.02mg is practically found.

According to Sauerbrunn et al.¹⁶ heavier pans generate high heat capacity calibration constants. To obtain accurate heat capacity data, it is recommended to use same pans preferably as light as possible, for calibration and sample analysis.

Data deconvolution

The total heat flow when calculated by MTDSC or DSC yield the same results when identical heating rates are employed.¹⁴ However, the values change depending on the experimental conditions such as

Number of modulations

Hill et al.¹⁴ analyzed spray dried lactose using hermetically sealed pans at 2⁰C/min heating rate, with periods ranging from 10 to 80 seconds. Cooling cycle was avoided by adjusting the modulation amplitude. Figure 10A shows that at shorter periods, the heat flow signals were sharper and taller compared to those heat flow signals at longer periods which were shorter and broader.

The software that deconvolutes the data uses one complete cycle to calculate the data points which resulted in smoothing effect (Figure 10B) with fewer cycles. Also the signals were noisy (Figure 10C) during transition phase such as crystallization peak with short periods but was visible with increased period. The author concludes that with fewer modulations through peak a rapid rise in heat flow takes place over one or two modulations which is calculated as change in amplitude, leading to apparent change in heat capacity.

Figure 10 A, Total heat flow; B, Modulated heat flow; C, Heat capacity analysis.

Large amplitudes resulting in cooling effect

Large amplitudes in temperature causes cooling effect in modulation cycle, though the heating rate is positive, influencing the melting and crystallization processes in the cycle. The maximum amplitude is given by

$amplitude = \frac{\left(heating rate \times period\right)}{2\pi \times 60}$

Type of pan used

Heat transfer to the sample depends on the type of pan used. Open pans might cause low heat capacity readings due to non-uniform distribution of sample at the base of the pan. This can be overcome by using non-hermetic pans as the sample is compressed and is in contact with the lid. Hermectic pans may or may not have sample in contact with the lid, but the contact can be improved by inverting the lid. However, it is important to make sure that the base of the pan is completely flat (Figure 11).

Figure 11 Different types of pans.

Craig et al.¹⁴ found that the type of pan affects the reproducibility of baselines. The following figure shows the baselines produced by open, non-hermetic, hermetic pans TA type and PE type with 2^ºC/min heating rate, period of 30s and 0.16^ºC amplitude. Initially reproducibility with TA hermetic pans was found to be poor, which was assumed due to poor thermal contact between pan and cell. Hence two methods were attempted in improving the contact by lightly sanding the base of the pan to ensure it was smooth to establish good contact, and by flattening the base of the pan with special made metal die before crimping on lid. But neither resulted in expected improvement in baseline reproducibility. The results obtained by another set of independent researchers, Varma-Nair et al.¹⁷ and Varma-Nair & Wunderlich,¹⁸ agreed with the findings of Craig et al.¹⁴ (Figure 12).

Figure 12 Baselines measured using.
(A) open pans, (B) non-hermetic pans, (C) hermetic (TA) pans, (D) hermetic (PE) pans

Figure 13 & Figure 14 are DSC and MTDSC signals for polyethylene terephthalate (PET) and polycarbonate (PC) blend. DSC signal for single compound PET (Figure 2) and the blend of PET and PC (Figure 13) are identical.^1,19 PC is an amorphous compound with Tg at 140^ºC. DSC failed to detect the Tg as the heat flow due to cold crystallization in PET occurs at the same temperature. This leads to incorrect calculation of PET crystallinity (12.2J/g), but in fact it should be zero J/g as PET is a quench cooled sample. But MTDSC signal clearly shows the Tg for Pc in reversing heat flow signal and thus allows the correct calculation of crystallinity of quench cooled PET.

Figure 13 DSC signal for PET and PC blend.

Figure 14 MTDSC signal for PET and PC blend.

Polymorphic studies

Different polymorphic forms have similar melting points and also undergo transition to different polymorphic forms during melting. MTDSC separates the overlapping phenomenon of melting and crystallization events which would otherwise not be possible by conventional DSC technique.

Bottom et al.²⁰ investigated different polymorphic forms and glass transition temperature of sulfapyridine using DSC and MDSC, thus demonstrating the use of MTDSC in investigating the polymorphic forms. Kawakami and Ida,²¹ applied MTDSC technique to demonstrate enantiotropic transitions in furosemide, tolbutamide and sulfanerazine, and thus explored the use of MTDSC in demonstrating enantiotropic transitions in well-known compounds. Manduva et al.²² investigated the polymorphic forms and kinetics of transitions in caffeine. Thus, the use of MTDSC in differentiating the polymorphs came into lime light. Qi and Craig,²³ demonstrated the use of MTDSC in investigating temperature induced transformations between α and γ indomethacin polymorphs, which were found to be monotropic transformation, involving melt-crystallization. Time dependent changes in heat capacity is studied by Grisedale et al.²⁴ in salbutamol and Raimi-Abraham et al.²⁵ in trehalose.

Characterization of channel hydrates

MTDSC is used to characterize salts, co-crystals, polymorphs, hydrates, solvates and various other solid state forms of drug substances. MTDSC is used to characterize the stoichiometric solid state forms of hydrates, non-stoichiometric hydrates or solvates also known as channel hydrates or solvates.²⁶

MTDSC is a better suitable technique in understanding the complex systems such as non-stoichiometric hydrates or solvates as they may reversibly loose or gain water or solvents depending on the prevailing environmental conditions particularly ambient relative humidity.

This technique would be highly useful in early drug developmental studies particularly in the early stages, during characterization of the raw materials used. One such example is the characterization of GNE068-PC, a novel development compound, was found to be mesomorphous with non-stoichiometric amounts of solvent (0.5% ethyl acetate) critical to the stability of the mesomorphous phase. Chakravarthy and Lubach et al.²⁷ identified the metastable forms of GNE068-PC formed by loss of solvent, particularly displaced by water at various RHs. They have employed MTDSC to study two distinct endothermic transitions one occurring between room temperature and 105^ºC attributing to solvent loss mostly water and the second one occurring at 130-150^ºC attributing to the loss of ethyl acetate. The enthalpy associated with second transition decreases with increasing temperature however, Tg remains unaffected by the amount of water present. The authors have attributed this to the lowering of entropy due to reduction in positional order within the structure due to loss of ethyl acetate.

Pharmaceutical formulations

Batch to batch variation in the composition of API, particularly in early drug developmental stages,²⁸ when the drug under investigation is crystalline with certain percent of amorphous blend, is problematic, leading to differences in degradation rates. Thus the composition plays a vital role drug stability as reported by Hasegawa et al.³⁰

Saklatvala et al.³¹ used MTDSC to investigate two different batches of drug L7 with different stability and sorption, and one batch with noticeable Tg and the other with no evident Tg. The authors conclude that the differences between the two batches id due to the presence on 5% amorphous material in one of the batches, while the other is more crystalline.

Nakai et al.³²; Huttenrauch,³³; York P,³⁴ reported the application of MTDSC in investigating the amorphous content in milled or micronized compounds obtained from high energy milling or micronization. Gunaseelan et al.²⁹ use MTDSC to quantify the amorphous compound to less than 1% in cefuroxime axetil induced during pharmaceutical processing such as milling, wet granulation and dry granulation.

Drug excipient compatability and drug compatability studies were investigated by Skotnicki et al.^35,36 in bisoprolol and valsartan. The authors concluded that the two compounds were incompatible i.e. if a fixed dosed formulation was made then the two compound should be physically separated by compacting them into bilayered tablet.

Thus MTDSC has more advantages than conventional DSC, where in the reversible and non-reversible events can be evaluated separately and heat capacities and heat capacity changes are calculated individually. MTDSC is a useful tool during the early stages of drug development in identifying different polymorphic forms, polymorphic transitions and also in determining the Tg of the drug substance. MTDSC also can also be a helpful tool in degradation studies in case of hydrates, solvates and channel hydrate compounds are involved. MTDSC al helps in understanding the polymorphic transitions from one form to another.

None.

The author declares there is no conflict of interest.

1. Verdonck E, Schaap K, Thomas LC. A discussion of the principles and applications of Modulated Temperature DSC (MTDSC). Int J Phar. 1999;192(1):3–20.
2. Reading M, Elliot D, Hill VL. MDSC, a new approach to the calorimetric investigation of physical and chemical transitions. J Therm Anal. 1992;40(3):949–955.
3. Reading M. Modulated differential scanning calorimetry–a new way forward in materials characterisation. Trends Polym Sci. 1993;1(8):248–253.
4. Boller A, Jin Y, Wunderlich B. Heat capacity measurement by modulated DSC at constant temperature. J Therm Anal. 1994;42(2-3):307–330.
5. Gmelin E. Classical temperature-modulated calorimetry: A review. Thermochimica Acta. 1997;304-305:1–26.
6. Leonard C, Thomas. An Introduction to the Techniques of Differential Scanning Calorimetry (DSC) and Modulated DSC®. New Castle, DE: TA Instruments Technical Paper; 2005.
7. Krishnan RV, Nagarajan K, Evaluation of heat capacity measurements by temperature-modulated differential scanning calorimetry. Journal of Thermal Analysis and Calorimetry. 2010;102(3):1135–1140.
8. Leonard C, Thomas. Modulated DSC® Paper #1 Why Modulated DSC®?;An Overview and Summary of Advantages and Disadvantages Relative to Traditional DSC. TA Instruments Technical Paper TP 006, New Castle, DE. USA; 2005.
9. Gill PS, Sauerbrunn SR, Reading M. Modulated differential scanning calorimetry. J Therm Anal. 1993;40(3):931–939.
10. Leonard C, Thomas. MDSC Paper #2, Modulated DSC® Basics; Calculation and Calibration of MDSC Signals. TA Instruments Technical Paper TP 007, New Castle, DE. USA; 2005.
11. Leonard C, Thomas. MDSC Paper #3, Modulated DSC®, Optimization of MDSC Experimental Conditions. TA Instruments Technical Paper TP 008, New Castle, DE. USA; 2005
12. Leonard C, Thomas. MDSC Paper #4, Advanced Tzero™ _MDSC®; Calculation of MDSC Signals, Including Phase Lag Correction. TA Instruments Technical Paper TP 010, New Castle, DE. USA: 2005.
13. Schawe JEK. Comparison of different evaluation methods in modulated temperature DSC. Thermochimica Acta. 1995;260:1–16.
14. Hill VL, Craig DQ, Feely LC. The effects of experimental parameters and calibration on MTDSC data. Int J Pharm. 1999;192(1):21–32.
15. Cao J, Long Y, Shanks RA, Experimental investigation into the heat capacity measurement using a modulated DSC. J Therm Anal. 1997;50(3):365–373.
16. Sauerbrunn SR, Gill PS, Foreman JA. Modulated DSC: The effect of period. Proceedings 23rd NATAS Conference; Sept. 25–28, Toronto, Canada. 1994.
17. Varma-Nair M, Wunderlich B, Balogh JJ. et al. Evaluation of non-isothermal heat capacities and applications of modulated DSC. Proceedins of the 23rd NATAS Conference; Sept. 25–28; Canada. 1994:26–31.
18. Varma-Nair M, Wunderlich B. Non-isothermal heat capacities and chemical reactions using a modulated DSC. J Therm Anal. 1996;46:(3-4)879–892.
19. Leonard C Thomas. MDSC Paper #5, Measurement of Glass Transitions and Enthalpic Recovery. 2005; 9.p.
20. Bottom R. The role of modulated temperature differential scanning calorimetry in the characterisation of a drug molecule exhibiting polymorphic and glass forming tendencies. Int J Pharm. 1999;192(1):47–53.
21. Kawakami K, Ida Y. Application of modulated-temperature DSC to the analysis of enantiotropically related polymorphic transitions. Thermochim Acta. 2005;427(1-2):93–99.
22. Manduva R, Kett VL, Banks SR, et al. Calorimetric and spatial characterization of polymorphic transitions in caffeine using quasi-isothermal MTDSC and localized thermomechanical analysis. J Pharm Sci. 2018;97(3):1285–1300.
23. Qi S, Craig DQM. The development of modulated, quasi-isothermal and ultraslow thermal methods as a means of characterizing the α to γ indomethacin polymorphic transformation. Mol Pharm. 2012;9(5):1087–1099.
24. Grisedale LC, Moffat JG, Jamieson MJ, et al. Development of photothermal FTIR microspectroscopy as a novel means of spatially identifying amorphous and crystalline salbutamol sulfate on composite surfaces. Mol. Pharm. 2013;10:815–1823.
25. Raimi-Abraham BT, Moffat JG, Belton PS, et al. Generation and characterization of standardized forms of trehalose dihydrate and their associated solid-state behavior. Cryst Growth Des. 2014;14(10):4955–4967.
26. Knopp MM, Löbmann K, Elder DP, et al. Recent advances and potential applications of modulated differential scanning calorimetry (mDSC) in drug development. Eur J Pharm Sci. 2016;87:164–173.
27. Chakravarty P, Lubach JW. Characterization of a water–solid interaction in a partially ordered system. Mol Pharm. 2013;10(11):4294–4300.
28. Rabel S, Jona J, Maurin M. Applications of modulated differential scanning calorimetry in preformulation studies. Journal of Pharmaceutical and Biomedical Analysis. 1999;21(2):339–345.
29. Gunaseelan S, Rao R, Manimaran A, et al. Determination of traces of amorphous cefuroxime axetil content in cefuroxime axetil crystalline drug substance using modulated differential scanning calorimetry (MDSC). J Chem Pharm Res. 2012;4:4743–4751.
30. Hasegawa J, Hanano M, Awazu S. Decomposition of acetylsalicylic acid and its derivatives in solid state. Chem Pharm Bull. 1975;23(1):86–97.
31. Saklatvala R, Royall PG, Craig DQM. The detection of amorphous material in a nominally crystalline drug using modulated temperature DSC — a case study. Int J Pharm. 1999;192(1):55–62.
32. Nakai Y, Fukuoka E, Nakajima S, et al. Crystallinity and physical characteristics of microcrystalline cellulose. Chem Pharm Bull. 1977;25(1):96–101.
33. Hüttenrauch R. Molekulargalenik als grundlage moderner arzneiformung. Acta Pharm Technol. 1978;6:55–127.
34. York P. Solid-state properties of powders in the formulation and processing of solid dosage forms. Int J Pharm. 1983;14(1):1–28.
35. Skotnicki M, Aguilar JA, Pyda M, et al. Bisoprolol and bisoprolol–valsartan compatibility studied by differential scanning calorimetry, nuclear magnetic resonance and x-ray powder diffractometry. Pharm Res. 2015;32(2):414–429.
36. Nichola J, Coleman, Duncan QM, et al. Modulated temperature differential scanning calorimetry: a novel approach to pharmaceutical thermal analysis. Int J Pharm. 1996;135(1-2):13–29.