
Technical Paper Volume 2 Issue 1
Local iRBF-DQ method for MHD duct flows at high hartmann numbers
Wang TC,1 Shen LH,1 Young DL,1
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Che CS2
1Department of Civil Engineering & Hydrotech Research Institute, National Taiwan University, Taiwan
2Department of Mathematics, University of Southern Mississippi, USA
Correspondence: Young DL , Department of Civil Engineering, National Taiwan University
Received: August 12, 2017 | Published: February 26, 2018
Citation: Wanga TC, Shena LH, Younga DL, et al. Local iRBF-DQ method for MHD duct flows at high hartmann numbers. MOJ App Bio Biomech. (2018);2(1):00047. DOI: 10.15406/mojabb.2018.02.00047
Download PDF
Abstract
In this paper, a localized integrated radial basis function-based differential quadrature (iRBF-DQ) method to solve steady, magnetohydrodynamic (MHD) duct flows is presented. Local iRBF-DQ method is a truly meshless and efficient method, which discretizes any derivative at a knot by weighted linear sum of functional values at its nearby nodes. The integrated RBF based approaches are more stable than conventional meshless procedure ones. The high Hartmann numbers (high magnetic field) MHD problems apply to the design of cooling systems with liquid metals for a thermal nuclear fusion blanket. We present results for Hartmann number up to
with fully insulating, partially insulating, and partially conducting walls, with the shapes of rectangular, circular or arbitrary cross sections. The results show that by using local iRBF-DQ method we can obtain accurate and stable approximations for the velocity and induced magnetic field at the range of Hartmann numbers of
aa
Keywords: meshless, iRBF collocation method, local iRBF-DQ method, MHD, Hartmann number
Abbreviations
MHD, magnetohydrodynamic; FDM, finite difference method; AFEM, analytical finite element method; RBFs, radial basis functions; PDEs, partial differential equations
Nomenclature
imposed magnetic field;
the angle between
and <
-axis;
,
-component of fluid velocity and dimensional form
dimensionless
-component of fluid velocity;
cdimensionless
-component of magnetic induction;
half channel width;
conductivity;
fluid dynamic viscosity;
permeability;
fluid density;
fluid pressure and pressure gradient;
coefficient of
;
,
-component of induced magnetic field and dimensional form;
-component and
-component of imposed magnetic field;
Hartmann number,
Hartmann number Multiplied
Hartmann number Multiplied
electric field;
current density vector;
fluid velocity vector;
imposed magnetic field;
magnetic induction
Introduction
Magnetohydrodynamics (MHD) is the study of the interaction between moving, conducting fluids and magnetic fields. In this paper, the discussion is restricted to incompressible, viscous and electrically conducting fluids through pipes and ducts under an imposed uniform, oblique magnetic field. The MHD issues have become increasingly important because of the practical engineering applications such as the design of cooling systems with liquid metals for a thermal nuclear fusion blanket. Blankets which rely only on the heat transverse ability of liquid metal are known as self-cooled liquid metal blankets. There are numbers of amount of data and papers concerning with the physical phenomena of liquid metal flows in the absence of a magnetic field. However, in a fusion reactor environment such as the first wall and the blankets, a strong magnetic field (high Hartmann numbers
Molokov S & Buhler L1,2 is necessary and confines the liquid-metal (electrically conducting) flows. The hydraulic and thermal behaviors of liquid metal flows in the existence of a magnetic field are quite diff erent fr om the behaviors of liquid metal flows without a magnetic field.3,4 Furthermore, the exact solutions of the MHD problems can only be obtained for some special cases.5,6 Therefore, it is important to explore a stable, accurate, and eff ective numerical method to obtain the approximate solutions of MHD problems.
Currently, researchers have investigated the two-dimensional MHD problem using several numerical methods. Singh & Lal7,8 solved MHD flows through pipes of triangular cross-section for small values of Hartmann number using finite difference method (FDM). Since it is hard to fit the arbitrary cross-section ofthe channel, the finite element method (FEM) for Hartmann number less than 10 was presented in.9-11 Tezer-Sezgin & Koksal12 used standard FEM with linear and quadratic elements for Hartmann numbers up to 100. Aft er that, Demendy and Nagy obtained the numerical solutions for Hartmann number
using analytical finite element method (AFEM).13 Furthermore, the boundary element method (BEM),14 and the fundamental solution method15 also have been used to obtain approximate solutions for MHD flow problems. To our best knowledge, the numerical results for MHD flow problems are mostly restricted to the moderate Hartmann numbers.
However, Nesliturk & Tezer-Sezgin16 have obtained the results for Hartmann numbers up to
is only for one case, a rectangular duct with partly conducting wall, which is computationally very expensive, due to the need of large memory and time consuming in building finer meshes. The difficulty for high Hartmann numbers is analogous to the advectiondiff usion equation. When advection process dominates diffusion, the physical values near the boundary would suddenly decrease to zero to satisfy boundary conditions and form very thin boundary layers. Radial basis functions (RBFs) have been originally developed for scattered data approximation, especially for higher dimensional problems. In recent years, RBFs have been further applied to solve numerical partial diff erential equations (PDEs). This new development is very useful due to the fact that this method is a truly mesh or grid free technique. Kansa17 initially published a series of papers in this area, and then Franke & Schaback18,19 were able to give a convergence proof and error bounds of numerical approach. In a comparative study, Franke20 surveyed an extensive number of techniques for interpolation/approximation. He concluded that overall the Multiquadrics (MQ) and Thin Plate Splines (TPS) are the most favorable techniques for scattered data approximation. Nevertheless, the accuracy of MQ depends on a shape parameter which is still an open research topic. Hence most applications of MQ used experimental tuning parameters or expensive optimization techniques to evaluate the optimum shape parameter.21 In this work, the integrated TPS is used as it combines good accuracy without the additional burden of computing a shape parameter.
Furthermore, integrated TPS is based on sound mathematical theory Duchon J22 whereas for
, although it works well, its construction theory is yet to be established.23 Furthermore, the numerical schemes based on RBFs to solve PDEs proposed up to date have one more feature concerned, which are based on function approximation. That is to say, these methods directly substitute the expression of function approximation by RBFs to a PDE, and aft er that we replace the dependent variables into the coefficients of function approximation. The process is very complex, especially for nonlinear problems. Later, Wu & Shu24 proposed a new approach using the so called RBF-DQ method, which focuses on the derivative approximation through the diff erential quadrature (DQ) methodology. The basic idea of the DQ method is that the derivatives of unknown function can be approximated as the function values at a group of nodes. Unfortunately, full exploitation of the feature of RBFs-based methods causes the ill-conditioned coefficient matrix as the rank increases. The RBF collocation method and RBF-DQ method also suff ered this kind of problem. To circumvent this difficulty, Kansa25 suggested substituting the global solvers into block partitioning and LU decomposition schemes for huge simulation problems. Shu & Yeo26 further proposed the local RBF-DQ method using local supporting nodes. Recently, Tran-Cong and his collaborators,27-31 further proposed the indirect radial basis function networks (IRBFN). They found that the IRBFN are more stable than the conventional RBF method. In the IRBFN approach, the RBF approximation is applied to a specific derivative of the solution function, and thus the solution function can be derived by integrating the derivative with the RBF expression. Consequently, the expressions of IRBFN are derived from integration of conventional RBFs. Mai-Duy & Tran-Cong27,28 proved that this procedure can have better approximation for the targeted derivative. Later, based on the idea of IRBFN, Shu & Wu32 proposed the local iRBF-DQ method to improve its performance.
The present paper is an application of techniques mentioned above, namely the iRBF collocation method and the local iRBF-DQ method, to the MHD duct flows. And its aim is to establish an accurate numerical approximation to the solutions of benchmark problems of MHD duct flows for the range of Hartmann number
. In general, the important range of Hartmann number in engineering practice is
. Since these two meshless methods are based on RBFs, they diff er fr om traditionally mesh-dependent numerical methods such as FEM with the need of meshing.
Problem physics
MHD equations derivation
The discussed geometry of cross section of blankets is restricted to the directions of imposed magnetic field lines which are orthogonal to the direction of flow velocity. We now consider a steady, laminar, fully developed flow with incompressible, viscous and finite conducting fluid in a duct which is infinitely long in
-direction. Hence, we can assume this is a two-dimensional duct flow along
and
directions.6
There is an imposed uniform, magnetic field
outside the field forming an angle
with the
-axis. The fluid velocity
is parallel to
-axis, the half channel width is
, and the origin is located at the center ofthe channel (Figure 1).
The Maxwell’s equations in steady state can be expressed as follows:
,(1)
, (2)
. (3)
For per unit charge, Ohm’s Law can be written as
. (4) from (1) and (2), we obtain
. (5 )
Through vector analysis, (5) can be written as follows
(6)
When we apply Biot-Savart Law and the incompressible fluid property,
and
both vanish, then (6) becomes:
. (7)
Adding Lorentz force (see Appendix A for more details) to the Navier-Stokes equations in a steady state problem, we have the following form:
. (8)
From (2) and using a vector identity, we have
(9)
Substituting (8) into (
, we will obtain the modified Navier-Stokes equations as follows:
. (10)
Notice that all physical values except pressure gradient are unchanged in the
-direction. Thus the fluid velocity
, the magnetic field
, and the pressure gradient
can be expressed in the following form:
, (11)
where
is the
-component fluid velocity,
is the induced magnetic field,
is a constant, and
(12)
are all constants.
The
-component of equations (7) and (10) becomes
(13)
(14)
It follows that we can substitute some non-dimensional variables [33]
(15)
into equations (13) and (14). Then we have the following non-dimensional form:
(16)
(17)
It is noted that there is a convenient independent dimensionless number, which is called Hartmann number,; and is defined by as follows:
, (18)
(19)
Equations (16) and (17) can be further simplified to the following forms:
, (20)
(21)
where
is assumed.
To facilitate easy reading, we omit the symbol and make and replace and
respectively in the following sections.
Boundary conditions
We consider the following simplified dimensionless coupled diff erential equations
, in (22)
, in, (23)
where
is the fluid region with the boundary
;
is the angle between imposed magnetic field and
-axis (
Figure 2). The general boundary conditions which are suitable in practice for the MHD problems can be expressed as:
where
with
. Let
be the insulated part and
be
the conducting part of the boundary
.
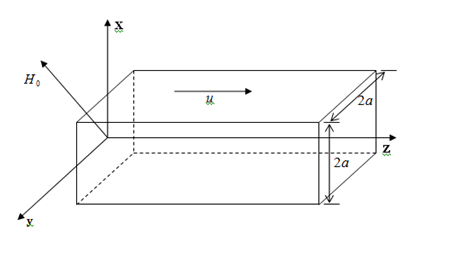
Figure 1Duct problem setting.
Numerical method
Decoupled governing equations
The MHD equations are coupled convection-diff usion equations. In general, solving coupled equations will consume more computational time and memory space than solving decoupled equations. Considering a rectangular duct with insulating walls, we can decouple the MHD equations.
First let us assume
; , (24)
where
is the velocity of the flow and
is the induced magnetic field. We can obtain decoupled equations by substituting the two variables (24) into MHD equations to get:
, in, (25)
<
, in(26)
on
>. (27)
This decoupled method is feasible only when the walls of the channel are insulated, which allows the two variables
and
which are assumed to be zeroes on
. In another case for partly insulating and partly conducting walls, we cannot do the decoupled process if the induced magnetic field is zero or no zero on
of the conducting part, so that the decoupled method is not possible. As a result, we have to solve the original coupled MHD equations (22) and (23) directly.
Radial basis functions
A m-th order integrated TPS is defined as
, (28)
where
is the Euclidean norm. Since
given by (28) is
, a
higher-order integrated Thin Plate Splines must be used.
Local
method
The basic idea of iRBF-DQ method was originated fr om the traditional DQ method. The basic approach of DQ method implies that the partial derivative of a continuous function at a reference node can be approximated by a weighted linear sum of function values at all discrete points within its support. Thus, DQ approximation of m-th order derivate with respect to
-direction at a reference node
can be expressed as
, (29)
where <
are the discrete nodes in the domain,
and the
are the values of function at supporting nodes and the related weighting coefficients respectively. In the local iRBF-DQ method, the number of each reference node corresponding to its supporting node can be diff erent and fixed. This means that, at any reference node, there is a supporting region, in which there are
supporting nodes which can be arbitrarily distributed. Then, the local iRBF-DQ approximation of m-th order derivative with respect to
-direction at a reference node
can be written as
(30)
where
is the Euclidean norm,
are the corresponding supportin
nodes near the reference node
is the number of supporting
nodes in the region,
and the
denote the function values at supporting
nodes and the related weighting coefficients respectively.
For the local iRBF-DQ method,
is chosen (i.e. integrated first-order TPS) as the basis functions. Integrated TPS can be obtained as follows
(31)
where
. By combining (30) and (31), we can obtain the values of corresponding coefficients for first-order derivative fr om the following system of equations:
(32)
For the given
, We can define
and express Eq. (32) as the numerical scheme form:
(33)
Substituting (32) into (
(26) and (27), we have
(34)
, on
, (35)
where
is the number of all discrete nodes in the domain, and
(36)
and
in (34) can be determined by the following numerical scheme:
(37)
(38)
and the velocity of the flow
and the induced magnetic field
can be obtained by (37) and (38). From (24), we have
(39)
collocation method
For iRBF collocation method, a
is used (i.e. integrated second-order TPS) to
guarantee at least
continuity for
and
. The approximation of function
and
, using integrated radial basis functions, can be written as a linear combination of
radial functions; i.e.,
, for (40)
, for < (41)
where
is the Euclidean norm,
is the number of data points,
is the vector position,
are coefficients to be determined, and
is the integrated radial basis function.
For any linear partial diff erential operator
, the governing equation can be written in the following matrix form<
(42)
where
(43)
(44) and
(45)
For a functionx, we can use the collocation method and obtain the following form by substituting (40) and (41) into (42):
(46)
, in
, (47)
on
, (48)
where
(49)
(50)
(51)
(52)
We can define
and combine the equations (46), (47)
into the global numerical scheme
(59)
(60)
It follows that
(61)
(62)
, for (63)
, for (64)
Thus,
and
can be obtained. From (24), we haves
(65)
Numerical Results
In this section we show the results of the MHD duct flows using the numerical methods introduced in the previous section. It is obvious that RBF collocation method and local RBF-DQ method do not need to mesh the complicated physical problems. In the following subsections, under diff erent influence of magnetic field and boundary conditions, the numerical results using small
, moderate
and
, high (10000), and even to
Hartmann numbers are obtained.
Shercliff
problem: imposed transverse magnetic field outside a square channel with insulating walls
The MHD flow is in along duct channel with a cross section
, and the angle
between
-axis and imposed magnetic field is
(Figure 3). Shercliff [5] proposed this example where the walls ofthe channel are insulated
. The velocity is zero on the solid walls
. In Tables 1&2, the approximate solutions of iRBF collocation method and local iRBF-DQ method for velocity at Hartmann number 100 on
are compared with uniform triangular element FEM and analytical solution, respectively. There are 10201 global nodes and 400 supporting nodes for local iRBF-DQ method, and 20000 elements for FEM. In Tables 1 and 2, we use 1681 and 2601 nodes for iRBF collocation method independently. The definition of relative error (i.e. R.E.) is
. We can find that the accuracy close to the walls becomes worse. In Figure 4, the relative errors at
of uniform FEM can only reach to at least about 10th power minus 1, but iRBF collocation method and local iRBF-DQ method can up to at least about 10th power minus 2 and 10th power minus 3, respectively. On the other hand, the relative errors at
of uniform FEM and iRBF collocation method can only reach to at least about 10th power minus 1, but local iRBF-DQ method can get up to at least about 10th power minus 2. In these tables, the exact solutions of velocity and magnetic induction are presented in,5.
In order to apply the approximation data to real blanket channels (high magneticfield), the high Hartmann numbers
MHD problems must be solved. In Figures 5&6, the approximate solutions of velocity and magnetic induction using iRBF collocation method are compared with the approximate solutions of local iRBF-DQ method for Hartmann number
and
. In Figure 7, the approximate solutions of velocity and magnetic induction using the local iRBF-DQ method at
is also presented independently. There are some oscillations near the walls of contour lines by iRBF collocation method as shown in Figures 5&6. However, the contour lines by local iRBF-DQ method are much smoother than by iRBF collocation method. The iRBF collocation method cannot obtain good numerical results of and
by the reason of ill-conditional matrix. However, local iRBF-DQ method can still obtain accurate numerical results of velocity and induced magnetic field, especially when Hartmann number is up to105. It can be seen that the boundary layers become thinner as Hartmann number increases (Figures 5-8). We also observe that the Hartmann number and the velocity and magnetic induction are varied inversely. It means that the values of velocity and magnetic induction approximate to 1/10 of their original values when Hartmann number becomes 10 times larger (see more detail in Appendix A).
Drectangular duct flow with insulating walls, under the influence of an oblique magnetic field
In this subsection, the numerical experiments are the same as the one in section 4.1 except the angle
between
-axis and imposed magnetic field changes fr om
to <
and
. In order to understand how diff erent angles between imposed magnetic field and
-axis will aff ect the velocity and magnetic induction, the approximate solutions of
and
by iRBF collocation method are compared with the approximate solutions of
and
by local iRBF-DQ method for
and
in section 4.2. In Figures 9&10, we approximate a medium high Hartmann number
and
, and the patterns show that the contour lines by iRBF collocation method are not smooth enough. There are some oscillations near the walls of velocity contour lines. We also show the capability to approximate the velocity and induced magnetic field by local iRBF-DQ method at
in Figure 11. The results show that as Hartmann number increases the boundary layers formation close to the walls for both velocity and magnetic induction is well observed. Velocity becomes stagnant at the center of the channel. We can also find an inverse ratio relationship between Hartmann numbers and the values of velocity and magnetic induction. It means that the values of velocity and magnetic induction approximate to
when Hartmann number becomes 10 times larger. local nodes In Figsures 12&13, we approximate a medium high Hartmann number
and <
and the patterns show that the contour lines by iRBF collocation method are more smoother than the contour lines for
. This is because that the symmetrical feature of
causes the velocity contour lines parallel to
. There are still some oscillations near the walls of velocity contour lines. We also show the capability to approximate the velocity and induced magnetic field by local iRBF-DQ method at
in Figure 14. The results show that as Hartmann number increases the boundary layers formation close to the walls for both velocity and magnetic induction is very obviously observed. The velocity becomes a little stagnant at the center of the channel. When external magnetic field applies obliquely, the boundary layers are concentrated near the corners in the direction of the field for both solutions of velocity and induced magnetic field. These are the well-known behaviors of the magnetohydrodynamic flows (see more details in Appendix A). We can also find an inverse ratio relationship between Hartmann number and the values of velocity and magnetic induction. It means that the values of velocity and magnetic induction approximate to
when Hartmann number becomes 10 times larger. In case 4.1 and case 4.2, we show the capability of our local iRBF-DQ method scheme to establish numerical approximations to the solution of MHD duct flows for different angles between imposed magnetic field and
-axis even at very high Hartmann numbers
Imposed transverse magnetic field outside a square channel with partly insulating walls andpartly conducting walls
In this subsection, we consider an external imposed transverse magnetic field
which is perpendicular to the wall at
. This wall is partly electrically conducted for a length
at the center (
Figure 15). The MHD flow is in a long duct channel with a cross section
, and the angle
between
-axis and imposed magnetic field is
In Figure 16&17, we compare the approximate solutions of iRBF collocation method with the approximate solutions of local iRBF-DQ method at high Hartmann numbers
and
. The patterns show that the contour lines by iRBF collocation method are almost the same with the contour lines by local iRBF-DQ method. However the approximate solutions near the walls of iRBF collocation method are worse than the approximate solution of local iRBF-DQ method. The contour lines near the edge by iRBF collocation method are not smooth enough. These figures show that there are more variations near the walls of velocity contour lines by iRBF collocation method as Hartmann number increases. However, the results for both
and
by local iRBF-DQ method are still accurate. We can find that the boundary layers become thinner as Hartmann number increases. In this case, the boundary layers are not only near to the walls but also inside the domain. Parabolic boundary layers are formed in the direction of imposed transverse magnetic field close to the discontinuity points
and
and thus cause three stagnant regions for the velocity (Figures 16&17). We can also find the dominant characteristics ofMHD flows at very high Hartmann numbers. Flow in the channel is totally separately into two rectangular flow regions with the boundary layers leaving the heart regions stagnant. Therefore our local iRBF-DQ scheme has the capability to deal with this kind boundary condition of MHD problems for high Hartmann numbers.
2-D circular duct flow with insulating walls, under the influence of an imposed transverse magnetic field
In this subsection, we consider the MHD flows in a long pipe channel with a radius of circular section
, and the angle
between
-axis and imposed magnetic field is
(
Figure 18). The walls of the channel are insulated
and the velocity is zero on the solid walls
. In
Figures 19-22, we presented the numerical results using the local iRBF-DQ method for Hartmann number
and 10000. We notice that the boundary layers become thinner as Hartmann number becomes larger. We can also find an inverse ratio relationship between Hartmann numbers and the values of velocity and magnetic induction. In this case, we show the local iRBF-DQ method is capable to produce good numerical results for the MHD circular pipe flows at exceptionally high Hartmann numbers. We observe that for the liquid metals used in fusion blankets the Hartmann number is high,
, i.e., the electromagnetic forces dominate over the viscous ones. Furthermore, the shapes of fusion blankets are mostly circular ducts. Thus, there is some superiority for using this meshless local iRBF-DQ method for solving the MHD circular pipe flow problems.
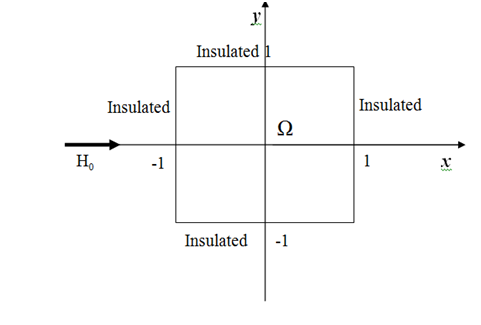
Figure 3Shercliff’s problem.
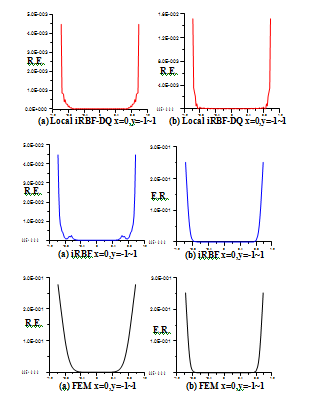
Figure 4 The comparison of relative errors of velocity.
Figure 5 The velocity and magnetic induction at
:(a)iRBF collocation method (61 61) and (b) local iRBF-DQ method (101 101); local nodes (20 20) 08.
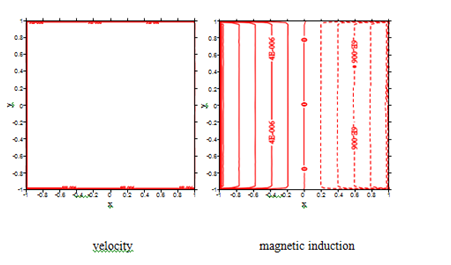
Figure 7 The velocity and magnetic induction oflocal iRBF-DQ method at
ge002_0009.gif" />
local iRBF-DQ method (401 401); local nodes(9 9) .
Figure 8 A rectangular flow with an oblique magnetic field.
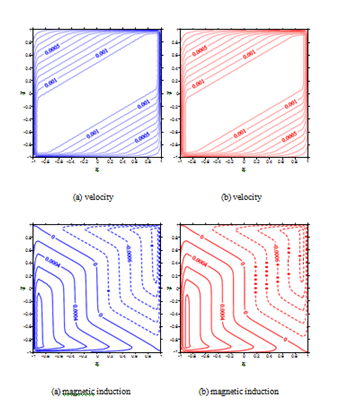
Figure 9 The velocity and magnetic induction at
: (a) iRBF collocation
method (61 61) and (b) local iRBF-DQ method (101 101); local nodes (20 20) 0.8.
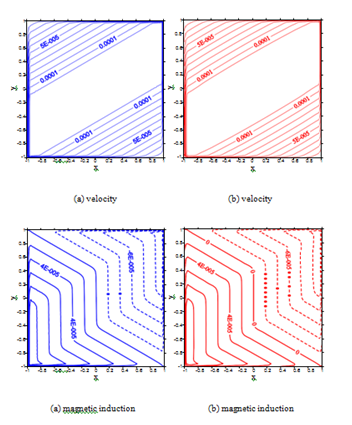
Figure 10 The velocity and magnetic induction at
: (a) iRBF
collocation method (81 81) and (b) local iRBF-DQ method (191 191); local nodes
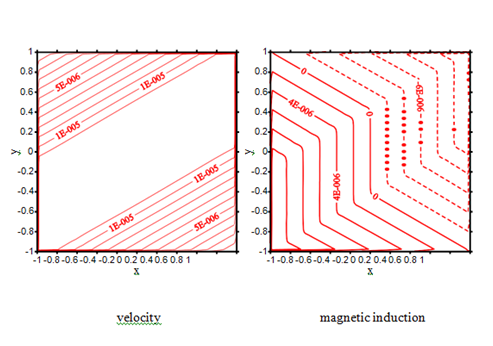
Figure 11 The velocity and magnetic induction oflocal iRBF-DQ method at, local iRBF-DQ method (401 401); local nodes .
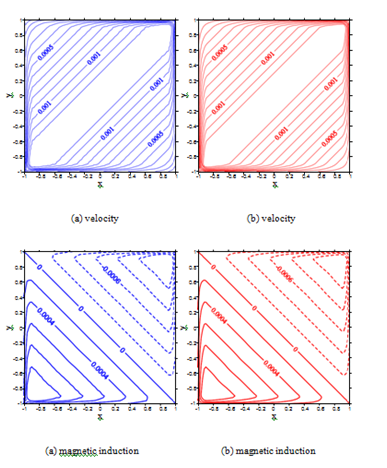
Figure 12 The velocity and magnetic induction at
:(a)iRBF
collocation method (61 61) and (b) local iRBF-DQ method (101 101); local nodes (2020).
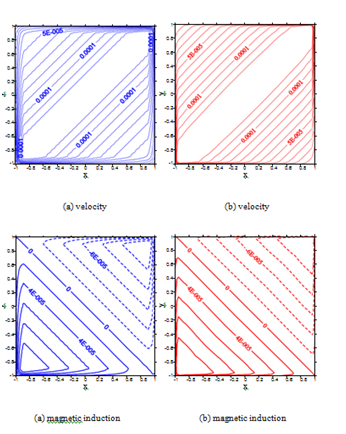
Figure 13 The velocity and magnetic induction at
:(a)iRBF
collocation method (81 81) and (b) local iRBF-DQ method (184 184); local nodes27
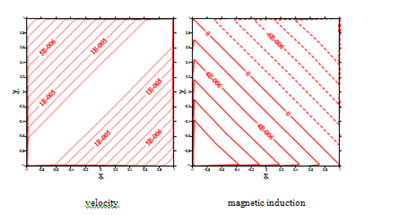
Figure 14 The velocity and magnetic induction oflocal iRBF-DQ method at , local iRBF-DQ method (391 391);
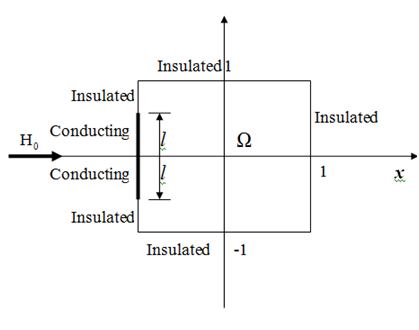
Figure 15 A rectangular flow with partly conducting walls.
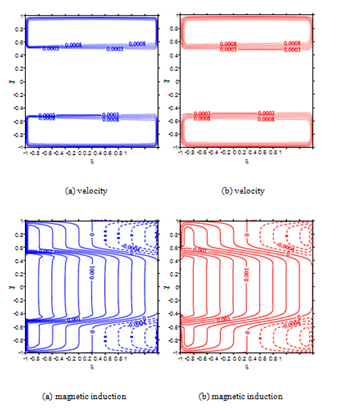
Figure 16 The velocity and magnetic induction at
:(a)iRBF collocation method(60 60) and (b) local iRBF-DQ method (101 101); local nodes (20 20).
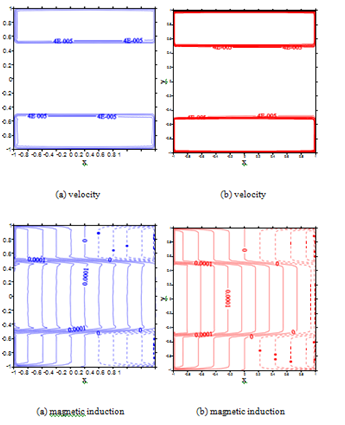
Figure 17 The velocity and magnetic induction at
:(a)iRBF collocation method(90 90) and (b) local iRBF-DQ method (299 299); local nodes .
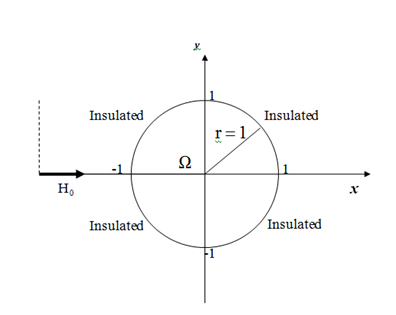
Figure 18 A circular flow with a transverse magnetic field.
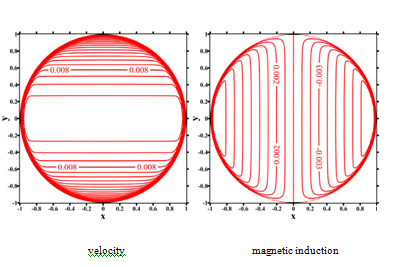
Figure 19 The velocity and magnetic induction oflocal iRBF-DQ method at
local iRBF-DQ method (71082) ; local nodes(138).
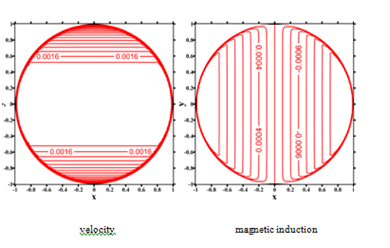
Figure 20The velocity and magnetic induction oflocal iRBF-DQ method at
local iRBF-DQ method (71082) ; local nodes(138).
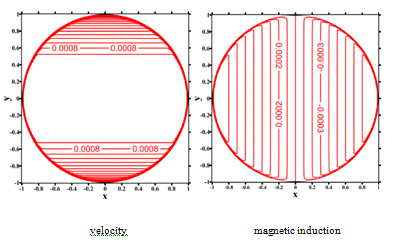
Figure 21The velocity and magnetic induction oflocal iRBF-DQ method at
local iRBF-DQ method (102263) ; local nodes (200).
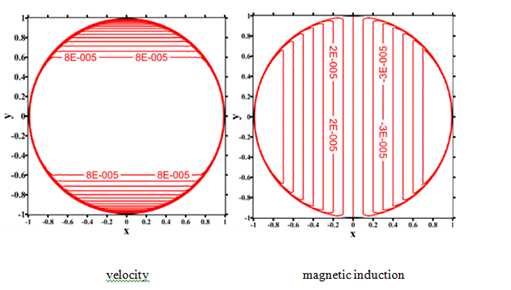
Figure 22The velocity and magnetic induction oflocal iRBF-DQ method at
local iRBF-DQ method (102263); local nodes(200).
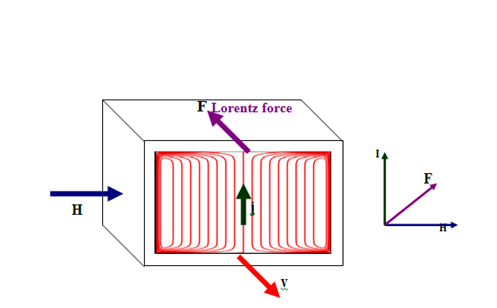
Figure 23Formation of MHD Lorentz force.
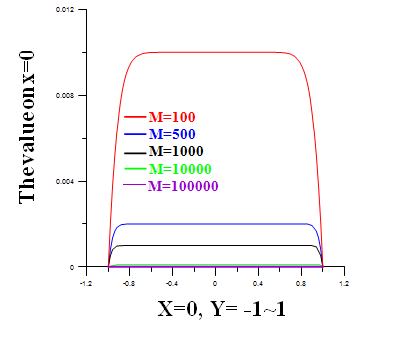
Figure 24The velocity contour lines when x = 0, y = -1 ~ 1 at M = 100 ~ 105.
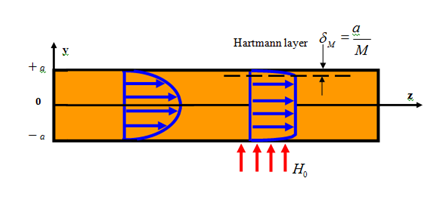
Figure 25 The diagram of Hartmann effect and Hartmann layer.
x |
y |
u (exact) |
u (FEM) |
u (iRBF) |
u (Local iRBF-DQ) |
R.E.(FEM) |
R.E.(iRBF) |
R.E. (Local iRBF-DQ) |
0.00 |
-0.98 |
2.06E-03 |
1.49E-03 |
1.97E-03 |
2.05E-03 |
-2.77E-01 |
-4.48E-02 |
-4.48E-03 |
0.00 |
-0.78 |
9.59E-03 |
8.75E-03 |
9.58E-03 |
9.58E-03 |
-8.69E-02 |
-6.61E-04 |
-1.72E-04 |
0.00 |
-0.58 |
9.99E-03 |
9.90E-03 |
1.00E-02 |
9.99E-03 |
-9.67E-03 |
5.89E-04 |
-5.93E-06 |
0.00 |
-0.38 |
1.00E-02 |
1.00E-02 |
1.00E-02 |
1.00E-02 |
-5.00E-04 |
-1.21E-05 |
3.96E-06 |
0.00 |
-0.18 |
1.00E-02 |
1.00E-02 |
1.00E-02 |
1.00E-02 |
-2.71E-05 |
-1.26E-05 |
5.76E-06 |
0.00 |
0.02 |
1.00E-02 |
1.00E-02 |
1.00E-02 |
1.00E-02 |
-1.30E-05 |
-1.21E-05 |
6.31E-06 |
0.00 |
0.22 |
1.00E-02 |
1.00E-02 |
1.00E-02 |
1.00E-02 |
-4.30E-05 |
-1.27E-05 |
5.66E-06 |
0.00 |
0.42 |
1.00E-02 |
9.99E-03 |
1.00E-02 |
1.00E-02 |
-9.40E-04 |
-6.39E-06 |
3.81E-06 |
0.00 |
0.62 |
9.98E-03 |
9.82E-03 |
1.00E-02 |
9.98E-03 |
-1.62E-02 |
1.55E-03 |
-1.41E-05 |
0.00 |
0.82 |
9.17E-03 |
8.08E-03 |
9.16E-03 |
9.17E-03 |
-1.19E-01 |
-1.61E-03 |
-2.62E-04 |
Table 1 The velocity comparison of local iRBF-DQ method, iRBF collocation method, FEM (uniform) and exact solution in Shercliff’s problem at M=100 on x=0, y=-1~1
x |
y |
u (exact) |
u (FEM) |
u (iRBF) |
u (Local iRBF-DQ) |
R.E.(FEM) |
R.E.(iRB) |
R.E. (Local iRBF-DQ) |
0.00 |
-0.98 |
8.29E-04 |
6.20E-04 |
7.66E-04 |
8.17E-04 |
2.52E-01 |
7.66E-02 |
1.52E-02 |
0.00 |
-0.78 |
2.00E-03 |
1.99E-03 |
2.05E-03 |
2.00E-03 |
2.64E-03 |
2.36E-02 |
9.20E-05 |
0.00 |
-0.58 |
2.00E-03 |
2.00E-03 |
2.05E-03 |
2.00E-03 |
1.01E-04 |
2.45E-02 |
7.80E-05 |
0.00 |
-0.38 |
2.00E-03 |
2.00E-03 |
2.05E-03 |
2.00E-03 |
7.39E-05 |
2.46E-02 |
5.50E-05 |
0.00 |
-0.18 |
2.00E-03 |
2.00E-03 |
2.05E-03 |
2.00E-03 |
6.32E-05 |
2.46E-02 |
4.45E-05 |
0.00 |
0.02 |
2.00E-03 |
2.00E-03 |
2.05E-03 |
2.00E-03 |
6.04E-05 |
2.46E-02 |
4.16E-05 |
0.00 |
0.22 |
2.00E-03 |
2.00E-03 |
2.05E-03 |
2.00E-03 |
6.37E-05 |
2.46E-02 |
4.50E-05 |
0.00 |
0.42 |
2.00E-03 |
2.00E-03 |
2.05E-03 |
2.00E-03 |
7.53E-05 |
2.46E-02 |
5.62E-05 |
0.00 |
0.62 |
2.00E-03 |
2.00E-03 |
2.05E-03 |
2.00E-03 |
1.05E-04 |
2.44E-02 |
7.69E-05 |
0.00 |
0.82 |
2.00E-03 |
1.98E-03 |
2.04E-03 |
2.00E-03 |
1.01E-02 |
2.24E-02 |
1.57E-04 |
Table 2 The velocity comparison of local iRBF-DQ method, iRBF collocation method, FEM (uniform) and exact solution in Shercliff’s problem at M=500 on x=0, y=-1~1
Conclusion
In this study, we have considered the application of local iRBF-DQ method to the MHD flow problems in a straight channel of uniform or arbitrary cross-sections. The main work of this investigation is an accurate approximation and easy implementation of the two-dimensional MHD flow problems. The results indicate that the local iRBF-DQ method is stable at moderate and high values of Hartmann number as comparing to the iRBF collocation method and FEM method. The localization feature reduces the computational time and solves the ill-condition problem of conventional RBFs methods. As the results shown we can conclude the present meshless local iRBF-DQ method can stably, accurately and quickly obtain the weighting coefficients of derivative approximation with arbitrary cross-sections even at very high Hartmann numbers in MHD flow problems.
Acknowledgement
Conflict of interests
The authors declare that there is no conflict of interest.
References
- Molokov S, Reed CB. Liquid metal magnetohydrodynamic flows in circular ducts at intermediate hartmann numbers and interaction parameters. Magnetohydrodynamics. 2003;39(4):539–546.
- Buhler L. Liquid metal magnetohydrodynamics for fusion blankets. In: Molokov S, Moreau R, editors. Magnetohydrodynamics, Historical Evolution and Trends. 2007.
- Branover H. Manetohydrodynamic Flow in Ducts. New York: Wiley and Sons; 1984.
- Garner RA, Lykoudis PS. Magneto-fluid-mechanic pipe flow in a transverse magnetic field, Part 2: Heat transfer. J Fluid Mech. 1997;48(1):29–141.
- Dragos L. Magneto-Fluid dynamics. Abacus Press, UK, 1975.
- Shercliff JA. Steady motion of conducting fluids in pipes under transverse magnetic fields. Proc Cambridge Philos Soc. 1953;49:136–144.
- Singh B, Lal J. MHD axial flow in a triangular pipe under transverse magnetic field. Indian J Pure Appl Math 1978;9:01–115.
- Singh B, Lal J. MHD axial flow in a triangular pipe under transverse magnetic field parallel to a side of the triangle. IndJ Techno.1979;117(5):184–189.
- Singh B, Lal J. FEM in MHD channel flow problems. Int J Numer Methods Eng. 1982;18(7):1104–1111.
- Singh B, Lal J. FEM for MHD channel flow with arbitrary wall conductivity. J Math Phys Sci. 1984;18:501–516.
- Singh B, Lal J. FEM for unsteady MHD flow through pipes with arbitrary wall conductivity. Int J Numer Methods Fluids. 1984;4(3):291–302.
- Tezer Sezgin CM. Koksal S, Finite element method for solving MHD flow in a rectangular duct. Int J Numer Methods Eng. 1989;28(2):445–459.
- Demendy Z, Nagy T. A new algorithm for solution of equations of MHD channel flows at moderate Hartmann numbers. Acta Mech 1997;123(4):135–149.
- Tezer–Sezgin CM, Han Aydn S, Solution of magnetohydrodynamic flow problems using the boundary element method. Eng Anal Bound Elem 2006;30(5): 411–418.
- Bozkaya C. Tezer Sezgin CM, Fundamental solution for coupled magnetohydrodynamic flow equations. J Comput Appl Math. 2007;203(1):125–144.
- Nesliturk AI, Tezer Sezgin CM, The finite element method for MHD flow at high Hartmann numbers. Comput Methods Appl Mech Eng. 2005;194(9–11):1201–1224.
- Kansa EJ. Multiquadrics: a scattered data approximation scheme with applications to computational fluid-dynamics. Comp Math Appl. 1990;19(8–9):147–161.
- Franke C, Schaback R, Solving partial diff erential equations by collocation using radial basis functions. Appl Math Comput 1998;93(1):73–82.
- Franke C, Schaback R. Convergence order estimates of mesh less collocation methods using radial basis functions. Adv Comput Math. 1998;8(4):381–399.
- Franke C, Scattered data interpolation: test of some methods. Math Comput. 1982;38:181–200.
- Carlson RE, Foley T. The parameter R in multiquadric interpolation. Comp Math App. 1991;21(9):29–42.
- Duchon J. Splines minimizing rotation invariant semi–norms in Sobolev spaces. Constructive Theory of Functions of Several Variables. 1977;38:85–100.
- Hardy RL. Theory and application of the multiquadric–biharmonic method. Comp Math Appl 1990;19(8–9):163–208.
- Wu YL, Shu C. Development of RBF-DQ method for derivative approximation and its application to simulate natural convection in concentric annuli. Comput Mech. 2002;29(6):477–485.
- Kansa EJ, Hon YC. Circumventing the ill-conditioning problem with multiquadric radial basis functions: applications to elliptic partial diff erential equations. Comput Math App. 2000;39(7–8):123–137.
- Shu C, Yeo KS. Local radial basis diff erential quadrature method and its application to solve two–dimensional incompressible Navier–Strokes equations. Comput Meth Appl Mech Eng. 2003;192(7–8):941–954.
- Mai Duy N, Tran Con T. Approximation of function and its derivatives using radial basis function networks. Appl Math Modelling. 2003;27(3):97–220.
- Mai Duy N, Tran Con T. Numerical solution of diff erential equations using multiquadric radial basis function networks. Neural Networks 2001;14(2):185–199.
- Ngo Cong D, Mai–Duy N, Karunasena K, et al. A numerical procedure based on –IRBFN and local MLS–ID–IRBFN methods for fluid–structure interaction analysis. CMES: Comput Modeling in Eng Sci. 2012;83(5):459–498.
- Thai Quang N, Le Cao K, Mai Duy N, et al. A numerical scheme based on compact integrated–RBFs and Adams Bash forth/Crank Nicolson algorithms for diffusion and unsteady fluid flow problems. Eng Anal Bound Elem. 2013;37(12):1657–1667.
- Ngo Cong D, Tien CM, Nguyen Ky T, et al. A generalised finite difference scheme based on compact integrated radial basis function for flow in heterogeneous soils. Int J Numer Meth Fluid. 2017;85(7):404–429.
- Shu C, Wu YL. Integrated radial basis functions–based diff erential quadrature method and its performance. Int J Numer Meth Fluid. 2007;53(6):969–84.
- Barrett KE. Duct flow with a transverse magnetic field at high Hartmann numbers. Int J Numer Meth Eng. 2001;50(8):1893–1906.

©2018 Wanga, et al. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.















