Electromagnetoelastic actuator for nanomedicine research

doi:10.15406/jnmr.2018.07.00192

Journal of

eISSN: 2377-4282

Nanomedicine Research

Mini Review Volume 7 Issue 4

Electromagnetoelastic actuator for nanomedicine research

Afonin SM

National Research University of Electronic Technology, Russia

Correspondence: Afonin SM, National Research University of Electronic Technology, Russia

Received: May 16, 2018 | Published: July 18, 2018

Citation: Afonin SM. Electromagnetoelastic actuator for nanomedicine research. J Nanomed Res. 2018;7(4):231-233. DOI: 10.15406/jnmr.2018.07.00192

Download PDF

Abstract

In this work the static and dynamic characteristics, the structural diagram and the transfer functions of the electromagnetoelasticactuator are obtained. The generalized structural diagram, the matrix transfer functions of the electromagnetoelastic actuator make it possible to describe the static and dynamic characteristics of the actuator with regard to its physical parameters, external load.

Keywords: electromagnetoelasticactuator, piezoactuator, structural diagram, transfer function, static and dynamic characteristics

Introduction

The electromagnetoelastic actuator for nanodisplacement on the piezoelectric, piezomagnetic, electrostriction, magnetostriction effects is used in the electromechanics systems for the nanomedicine research in the scanning sensing microscopy and the adaptive optics.^1‒8 For designing the nanotechnology equipment the static and dynamic characteristics, the mathematical model, the structural diagram and transfer functions of the electromagnetoelastic actuator are calculated.^9‒18 The mathematical model, the structural diagram and transfer functions the electromagnetoelastic actuator based on the electromagnetoelasticity make it possible to describe the dynamic and static properties of the electromagnetoelastic actuator for the nanomedicine research with regard to its physical parameters and external load.^19‒24 The static and dynamic characteristics, the mathematical model, the structural diagram and transfer functions of the electromagnetoelastic actuator are used for the nanomedicine research with the scanning sensing microscopy.

Structural diagram

Let us consider the structural diagram of the electromagnetoelastic actuator for the nanomedicine research in contrast Cady and Mason electrical equivalent circuits. The method of mathematical physics is applied for the solution the wave equation and for the determination the structural diagram of the electromagnetoelastic actuator for nanomedicine research.^1‒18The mathematical model and the generalized structural diagram of the actuator ^7,14on (Figure 1) are determined,using method of the mathematical physics for the joints solution of the wave equation, the boundary conditions and the equation of the electromagnet elasticity, in the form

$\begin{matrix} Ξ_{1} (p) = {[1 / (M_{1} p^{2})]} \times \times {- F_{1} (p) + {(1 / χ_{i j}^{Ψ})} [ν_{m i} Ψ_{m} (p) - {[γ / sh (l γ)]} [ch (l γ) Ξ_{1} (p) - Ξ_{2} (p)]]} \end{matrix}$ $\begin{array}{l} Ξ_{1} (p) = {[1 / (M_{1} p^{2})]}^{} \times \\ \times {- F_{1} (p) + {(1 / χ_{i j}^{Ψ})}_{}^{} [ν_{m i} Ψ_{m} (p) - {[γ / sh (l γ)]}_{} [ch (l γ) Ξ_{1} (p) - Ξ_{2} (p)]]} \end{array}$ (1)
$\begin{matrix} Ξ_{2} (p) = {[1 / (M_{2} p^{2})]} \times \times {- F_{2} (p) + {(1 / χ_{i j}^{Ψ})} [ν_{m i} Ψ_{m} (p) - {[γ / sh (l γ)]} [ch (l γ) Ξ_{2} (p) - Ξ_{1} (p)]]} \end{matrix}$ $\begin{array}{l} Ξ_{2} (p) = {[1 / (M_{2} p^{2})]}^{} \times \\ \times {- F_{2} (p) + {(1 / χ_{i j}^{Ψ})}_{}^{} [ν_{m i} Ψ_{m} (p) - {[γ / sh (l γ)]}_{} [ch (l γ) Ξ_{2} (p) - Ξ_{1} (p)]]} \end{array}$ (2)
Where $v_{m i} = ⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} d_{33}, d_{31}, d_{15} g_{33}, g_{31}, g_{15} d_{33}, d_{31}, d_{15} \end{matrix}$ $v_{m i} = {\begin{matrix} d_{33}, d_{31}, d_{15} \\ g_{33}, g_{31}, g_{15} \\ d_{33}, d_{31}, d_{15} \end{matrix}$ , $Ψ_{m} = ⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} E_{3}, E_{1} D_{3}, D_{1} H_{3}, H_{1} \end{matrix}$ $Ψ_{m} = {\begin{matrix} E_{3}, E_{1} \\ D_{3}, D_{1} \\ H_{3}, H_{1} \end{matrix}$ , $s_{i j}^{Ψ} = ⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ \begin{matrix} s_{33}^{E}, s_{11}^{E}, s_{55}^{E} s_{33}^{D}, s_{11}^{D}, s_{55}^{D} s_{33}^{H}, s_{11}^{H}, s_{55}^{H} \end{matrix}$ $s_{i j}^{Ψ} = {\begin{matrix} s_{33}^{E}, s_{11}^{E}, s_{55}^{E} \\ s_{33}^{D}, s_{11}^{D}, s_{55}^{D} \\ s_{33}^{H}, s_{11}^{H}, s_{55}^{H} \end{matrix}$ (3)
$c^{Ψ} = ⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} c^{E} c^{D} c^{H} \end{matrix}$ $c^{Ψ} = {\begin{matrix} c^{E} \\ c^{D} \\ c^{H} \end{matrix}$ , $γ = ⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} γ^{E} γ^{D} γ^{H} \end{matrix}$ $γ = {\begin{matrix} γ^{E} \\ γ^{D} \\ γ^{H} \end{matrix}$ , $l = ⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} δ h b \end{matrix}$ $l = {\begin{matrix} δ \\ h \\ b \end{matrix}$ , $χ_{i j}^{Ψ} = s_{i j}^{Ψ} / S_{0}$ $χ_{i j}^{Ψ} = s_{i j}^{Ψ} / S_{0}$ (4)

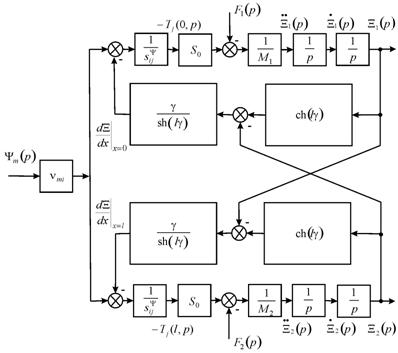
Figure 1 Generalized structural diagram of electromagnetoelastic actuator for the nanomedicine research.

v_miis the coefficient electromagnetoelasticity, $Ψ_{m} = {E_{m}, D_{m}, H_{m}$ $Ψ_{m} = {E_{m}, D_{m}, H_{m}$ is the control parameter, E_m is the electric field strength for the voltage control along axis m, D_m is the electric induction for the current control along axis m, H_mfor magnetic field strength control along axis m, d_miis the piezomoduleat the voltage-controlled piezoactuator or the coefficient of the magnetostriction at the magnetostrictive actuator, g_mi is the piezomoduleat the current-controlled piezoactuator, $s_{i j}^{Ψ}$ $s_{i j}^{Ψ}$ is the elastic complianceat Y = const, S₀is the cross section area, M₁, M₂ are the mass on the faces of the actuator, $Ξ_{1} (p)$ $Ξ_{1} (p)$ , $Ξ_{2} (p)$ $Ξ_{2} (p)$ and $F_{1} (p)$ $F_{1} (p)$ , $F_{2} (p)$ $F_{2} (p)$ are the Laplace transforms of the appropriate displacements and the forces on the faces 1, From equations of the forces acting on the faces of the actuator, the equation of the electromagnetoelasticity, the wave equation we obtain the generalized structural diagram of the electromagnetoelastic actuator. The structural diagrams of the voltage-controlled or current-controlled piezoactuator are determined from the mathematical model of the electromagnetoelastic actuator. (Figure 1) The generalized transfer functions of the of the electroelastic actuator are the ratio of the Laplace transform of the displacement of the face actuator and the Laplace transform of the corresponding control parameter or the force at zero initial conditions.

Characteristics of electromagnetoelastic actuator

The matrix transfer function of the actuator is deduced from its mathematical model (4)^8,14,18 in the form

$(Ξ (p)) = (W (p)) (P (p))$ $(Ξ (p)) = (W (p)) (P (p))$ (5)

$(Ξ (p)) = (\begin{matrix} Ξ_{1} (p) Ξ_{2} (p) \end{matrix})$ $(Ξ (p)) = (\begin{matrix} Ξ_{1} (p) \\ Ξ_{2} (p) \end{matrix})$ ,

$(W (p)) = (\begin{matrix} \begin{matrix} W_{11} (p) & W_{12} (p) & W_{13} (p) \end{matrix} \begin{matrix} W_{21} (p) & W_{22} (p) & W_{23} (p) \end{matrix} \end{matrix})$ $(W (p)) = (\begin{matrix} \begin{matrix} W_{11} (p) & W_{12} (p) & W_{13} (p) \end{matrix} \\ \begin{matrix} W_{21} (p) & W_{22} (p) & W_{23} (p) \end{matrix} \end{matrix})$

(P (p)) = ⎛ ⎜ ⎝ \begin{matrix} Ψ_{m} (p) F_{1} (p) F_{2} (p) \end{matrix} ⎞ ⎟ ⎠

$(P (p)) = (\begin{matrix} Ψ_{m} (p) \\ F_{1} (p) \\ F_{2} (p) \end{matrix})$

Where $(Ξ (p))$ $(Ξ (p))$ is the column-matrix of the Laplace transforms of the displacements for the faces of the electromagnetoelastic actuator, (W(p)) is the matrix transfer function, (P(p)) the column-matrix of the Laplace transforms of the control parameter and the forces.

At $Ψ_{m} = E_{3}$ $Ψ_{m} = E_{3}$ and v_mi =d₃₁ we have transfer functions of the piezoactuator in the form

W_{11} (p) = Ξ_{1} (p) / E_{3} (p) = {d_{31} {[M_{2} χ_{11}^{E} p^{2} + γ th (h γ / 2)]} / A}_{11}

$W_{11} (p) = Ξ_{1} (p) / E_{3} (p) = {d_{31} {[M_{2} χ_{11}^{E} p^{2} + γ th (h γ / 2)]}_{}^{} / A}_{11}$

χ_{11}^{E} = s_{11}^{E} / S_{0}

$χ_{11}^{E} = s_{11}^{E} / S_{0}$

\begin{matrix} A_{11} = M_{1} M_{2} {(χ_{11}^{E})}^{2} p^{4} + {(M_{1} + M_{2}) χ_{11}^{E} / [c^{E} th (h γ)]} p^{3} + + [(M_{1} + M_{2}) χ_{11}^{E} α / th (h γ) + 1 / {(c^{E})}^{2}] p^{2} + 2 α p / c^{E} + α^{2} \end{matrix}

$\begin{array}{l} A_{11} = M_{1} M_{2} {(χ_{11}^{E})}^{2} p^{4} + {(M_{1} + M_{2}) χ_{11}^{E} / [c^{E} th (h γ)]} p^{3} + \\ + [(M_{1} + M_{2}) χ_{11}^{E} α / th (h γ) + 1 / {(c^{E})}^{2}] p^{2} + 2 α p / c^{E} + α^{2} \end{array}$

W_{21} (p) = Ξ_{2} (p) / E_{3} (p) = {d_{31} {[M_{1} χ_{11}^{E} p^{2} + γ th (h γ / 2)]} / A}_{11}

$W_{21} (p) = Ξ_{2} (p) / E_{3} (p) = {d_{31} {[M_{1} χ_{11}^{E} p^{2} + γ th (h γ / 2)]}_{}^{} / A}_{11}$

W_{12} (p) = Ξ_{1} (p) / F_{1} (p) = - {χ_{11}^{E} {[M_{2} χ_{11}^{E} p^{2} + γ / th (h γ)]} / A}_{11}

$W_{12} (p) = Ξ_{1} (p) / F_{1} (p) = - {χ_{11}^{E} {[M_{2} χ_{11}^{E} p^{2} + γ / th (h γ)]}_{}^{} / A}_{11}$

\begin{matrix} W_{13} (p) = Ξ_{1} (p) / F_{2} (p) = = W_{22} (p) = Ξ_{2} (p) / F_{1} (p) = {[χ_{11}^{E} γ / sh (h γ)] / A}_{11} \end{matrix}

$\begin{array}{l} W_{13} (p) = Ξ_{1} (p) / F_{2} (p) = \\ = W_{22} (p) = Ξ_{2} (p) / F_{1} (p) = {[χ_{11}^{E} γ / sh (h γ)] / A}_{11} \end{array}$

W_{23} (p) = Ξ_{2} (p) / F_{2} (p) = - {χ_{11}^{E} {[M_{1} χ_{11}^{E} p^{2} + γ / th (h γ)]} / A}_{11}

$W_{23} (p) = Ξ_{2} (p) / F_{2} (p) = - {χ_{11}^{E} {[M_{1} χ_{11}^{E} p^{2} + γ / th (h γ)]}_{}^{} / A}_{11}$

The static characteristics of the actuator $ξ_{1} (\infty)$ $ξ_{1} (\infty)$ and $ξ_{2} (\infty)$ $ξ_{2} (\infty)$ have the form

$ξ_{1} (\infty) = ν_{m i} Ψ_{m 0} l (m / 2 + M_{2}) / (m + M_{1} + M_{2})$ $ξ_{1} (\infty) = ν_{m i} Ψ_{m 0} l (m / 2 + M_{2}) / (m + M_{1} + M_{2})$ (6)

$ξ_{2} (\infty) = ν_{m i} Ψ_{m 0} l (m / 2 + M_{1}) / (m + M_{1} + M_{2})$ $ξ_{2} (\infty) = ν_{m i} Ψ_{m 0} l (m / 2 + M_{1}) / (m + M_{1} + M_{2})$ (7)

The generalized structural scheme and the generalized transfer functions of the electromagnetoelastic actuator nano- and micro displacement are obtained from the generalized structural parametric model of the electromagnetoelastic actuator for the precision mechanics.

$ξ_{1} (\infty) + ξ_{2} (\infty) = ν_{m i} Ψ_{m 0} l$ $ξ_{1} (\infty) + ξ_{2} (\infty) = ν_{m i} Ψ_{m 0} l$ (8)

Where $m, M_{1}, M_{2}$ $m, M_{1}, M_{2}$ are the mass of the actuator and load masses.

Let us consider the voltage-controlled the piezoactuator from PZT at the longitudinal piezo effect for $m < < M_{1}$ $m < < M_{1}$ , $m < < M_{2}$ $m < < M_{2}$ .At $d_{33} = 4 \cdot 10^{- 10}$ $d_{33} = 4 \cdot 10^{- 10}$ m/V, U=150 V, M₁ =1kg, M₂=4kg the static characteristics of the actuatorhave following form $ξ_{1} (\infty) = 48$ $ξ_{1} (\infty) = 48$ nm, $ξ_{2} (\infty) = 12$ $ξ_{2} (\infty) = 12$ nm, $ξ_{1} (\infty) + ξ_{2} (\infty) = 60$ $ξ_{1} (\infty) + ξ_{2} (\infty) = 60$ nm.

The transfer function of the voltage-controlled transverse piezoactuator at , $M_{1} \to \infty$ $M_{1} \to \infty$ have the form

m < < M_{2}

$m < < M_{2}$ ,

W (p) = \frac{Ξ_{2} (p)}{U (p)} = \frac{k_{a 11}}{T_{t 11}^{2} p^{2} + 2 T_{t 11} ξ_{t 11} p + 1}

$W (p) = \frac{Ξ_{2} (p)}{U (p)} = \frac{k_{a 11}}{T_{t 11}^{2} p^{2} + 2 T_{t 11} ξ_{t 11} p + 1}$

k_{a 11} = \frac{d_{31} h / δ}{1 + C_{e} / C_{11}^{E}}

$k_{a 11} = \frac{d_{31} h / δ}{1 + C_{e} / C_{11}^{E}}$

$T_{t 11} = \sqrt{M_{2} / (C {}_{e}+ C_{11}^{E})}$

$ξ_{t 11} = α h^{2} C_{11}^{E} / (3 c^{E} \sqrt{M_{2} (C_{e} + C_{11}^{E})})$

Were T_t11is the time constant and $ξ_{t 11}$ is the damping coefficient for the piezoactuator. At $M_{1} \to \infty$ , $m < < M_{2}$ . d₃₁= 2.10^-10m/V, $h / δ = 20$ , M₂ = 1kg, $C_{11}^{E} = 2.4 \cdot 10^{7}$ N/m, $C_{e} = 0.1 \cdot 10^{7}$ H/m the parameters of the transfer function have the form $k_{a 11} = 3.84$ nm/V, T_t11= 0.2.10^-3 c. Accordingly the static and dynamic characteristics of the voltage-controlled transverse piezoactuator for the nanomedicine research are determined.

Conclusion

The static and dynamic characteristics, the mathematical model, the structural diagram and transfer functions of the electromagnetoelastic actuator for the nanomedicine research are obtained. The generalized structural diagram, the transfers functions of the electromagnetoelastic actuator make it possible to describe the dynamic and static properties of the actuator with regard to its physical parameters, external load.