One of the most important applications of graphene is in the field of polymer nanocomposites, where graphene is introduced as filler with the aim to improve their chemical and physical properties. Such as polystyrene (PS), PMMA, PVA, polypropylene (PP), epoxy, polyester, silicon foams, polyurethanes (PU) and polycarbonates (PC), graphene-based nanomaterials have been utilized in a myriad of bioapplications (e.g., drugs and gene delivery, nanomedicine, bioimaging and potential cancer therapies). The graphene, Polyurethane (PU), calcium carbonate (CC) and absorption of CC in graphene/PU composite, respectively were studied using theoretical calculations like Gibbs free energy, log P, Fourier Transform Infrared (FTIR) and electrostatic potential. FTIR spectroscopy reveals information about the molecular interactions of chemical components and is useful for characterization of composite. Nucleophilic and electrophilic regions were calculated using the electrostatic potential. It was determined that the hydrophilic (log P, octanol–water distribution constant) values play an important role in the absorption process of CC.

 Keywords: Graphene, Polyurethane, Modeling, Composites

PS, Polystyrene; PP, Polypropylene; PU, Polyurethanes; PC, Polycarbonates; CC, Calcium Carbonate; FTIR, Fourier Transform Infrared; WPU, Waterborne Polyurethane; FGS, Functionalized Graphene Sheet; TPU, PU-Thermoplastic; AM1, Austin Model 1; ANNs, Artificial Neural Networks; SOM, Self-Organization Map; BP, Backward Propagation

The field of nanoscience has blossomed over the last two decades and the importance of nanotechnology increase in areas such as computing, sensors, biomedical and many other applications. In this field the discovery of graphene and graphene–based polymer nanocomposites is an important addition in the field of nanoscience. The physicochemical properties of the nanocomposite depend on the distribution of graphene layers in the polymer matrix as well as interfacial bonding between the graphene layers and polymer matrix.¹ Graphene can be described as a one-atom thick.² layer of graphite. It is the basic structural element of other allotropes, including graphite, charcoal, carbon nanotubes and fullerenes.

It can also be considered as an indefinitely large aromatic molecule, the limiting case of the family of flat polycyclic aromatic hydrocarbons.^3-5 The composites with graphene have been prepared with a number of polymers, mainly polyurethane (PU), which can provide properties covering from a high performance elastomer to tough thermoplastic with diexcellent physical properties, including high tensile strength, abrasion and tear resistance and solvent resistance. In addition, its high versatility in chemical structures originated from a wide range of monomer materials affords tailor–made properties with well–designed combinations of these monomers. As a result, PU can be easily manipulated to satisfy the highly diversified demands of modern technologies.

In order to decrease emissions of volatile organic compounds, the development of environmentally friendly waterborne polyurethane (WPU) has been increasing, especially in the field of coating industry where the reduction of evolution of volatile organic compounds during the drying process is critical. In addition, WPU offers many advantages such as low viscosity at high molecular weight and good applicability, which cannot be realized with conventional solvent–borne systems .⁶ Lee et al.⁷ prepared water-borne polyurethane (WPU)/functionalized graphene sheet (FGS) nanocomposites by in situ method. The electrical conductivity of the nanocomposite was increased 10⁵–fold compared to pure WPU due to homogeneous dispersion of FGS particles in WPU matrix. The presence of FGS also increased the melting temperature and heat of fusion of the soft segment of WPU in the nanocomposites.

Liang et al. ⁸ prepared three types of nanocomposites by solution mixing process. They used isocyanate modified graphene, sulphonated graphene and reduced graphene as nanofiller and PU-thermoplastic (TPU) as the matrix polymer. The rate of thermal degradation of TPU/isocyanate modified graphene nanocomposites is much higher than that of TPU/sulphonated graphene and TPU/reduced graphene nanocomposites. There has been a surge of interest in developing graphene for drug loading and delivery because strong interaction exists between hydrophobic drugs and aromatic regions of graphene sheets. Dai’s group initially developed NGO–PEG (nanographene oxide–polyethylene glycol) as a nanocarrier to load variant anticancer drugs via nancovalent physisorption and evaluated it’s in vitro cellular uptake capacity and photo luminescent property.^9-10

Quantum chemical calculations produce a large amount of output data. Therefore it is important to decide which output is elevated for the chemical, biochemical, or biological mechanism underlying the phenomenon under investigation.¹¹ The PM3 semi empirical method (Parameterized Model number 3), is selected (the Hyperchem software, release 7.0, being used). This method can automatically optimize the bond length, angle and twist angle and yield a lot of information on the structure; define and select the output parameter. PM3 uses a Hamiltonian that is very similar to the AM1 (Austin Model 1) Hamiltonian but the parameterization strategy is different. While AM1 was parameterized largely based on a small number of atomic data, PM3 parameterized to reproduce a large number of molecule´s properties. In some sense, chemistry gave way to statistics with the PM3 model. Different parameterization and slightly different treatment of nuclear repulsion allow PM3 to treat hydrogen bonds rather well but it amplifies non–physical hydrogen–hydrogen attractions in other cases. This results in serious problems when analyzing intermolecular interactions (methane is predicted to be a strongly–bound dimmer) or conformations of flexible molecules (OH is strongly attracted to CH3 in 1–pentanol). The accuracy of thermochemical predictions with PM3 is slightly better than of AM1. The PM3 model has been widely used for rapid estimation of molecular properties and has been recently extended to include many elements, including some transitions metal.^12-13

In the past decade, artificial neural networks (ANNs) have received a great deal of attention among scientists and engineers and they are being touted as one of the greatest computational tools ever developed. Much of this excitement is due to the ability of neural networks to emulate the brain’s ability to learn by example. Specifically, ANNs are known to be a powerful tool to simulate various non-linear systems and have been applied to numerous problems of considerable complexity in many fields, including engineering, psychology, medicinal chemistry, diagnostics and pharmaceutical research.¹⁴ The application of ANNs in the field of pharmaceutical development and optimization of the dosage forms has become a topic of discussion in the pharmaceutical literature.¹⁵

The potential applications of ANNs methodology in the pharmaceutical sciences are broad as ANNs capabilities can be summarized by modeling, pattern recognition and prediction. Thus, applications of ANNs include drug modeling, dosage design, protein structure and function prediction, pharmacokinetics and pharmacodynamics modeling, as well as, interpretation of analytical data and in vitro/in vivo correlations.¹⁴

In this project the study of absorption process of CC was realized using PM3-semiempirical method for determine ΔG, structural parameters, FTIR and MESP of PU, Graphene, PU/Graphene composite and through data of bond lengths, bond angles and energies, the calculous were compared with ANNs for verified the absorption process.

Geometry optimization

In this study the semiempirical method was used for describing the potential energy function of the system. The optimizing process of structures used in this work carried out using the PM3 method, because it generates a lower-energy structure even when the initial structure is far away from the minimum structure. The Polak–Ribiere algorithm was used for mapping the energy barriers of the conformational transitions. For each structure, 1050 iterations, a level convergence of 0.001kcal mol Å and a line search of 0.1 were carried out.¹⁶

Structural parameters

The optimized structural parameters were used in the vibration wavenumber calculation with PM3 method to characterize all stationary points as minima. The structural parameters were calculated select the Constrain bond and length options of Build menu for two methods of analysis.

FTIR

The FTIR was obtained by first selecting menu Compute, vibrational, rotational option, once completed this analysis, using the option vibrational spectrum of FTIR spectrum pattern is obtained from the method of analysis.¹⁷

Electrostatic potential

After obtaining a Gibbs free energy or optimization geometry using the PM3 method, we can plot two–dimensional contour diagrams of the electrostatic potential surrounding a molecule, the total electronic density, the spin density, one or more molecular orbitals and the electron densities of individual orbitals. Hyperchem software displays the electrostatic potential as a contour plot. Choose the values for the starting contour and the contour increment so that you can observe the minimum (typically about –0.5 for polar organic molecules) and so that the zero potential line appears.¹⁸

Artificial neuronal networks (ANNs)

One of the more important ANN is the Self-Organization Map (SOM) proposed by Kohonen. In this network there is an input layer and the Kohonen layer, which is usually, designed as two-dimensional arrangement of neurons that maps n-dimensional input to two-dimensional. It is basically a competitive network with the characteristic of self-organization providing a topology-preserving mapping from the input space to the clusters. Mathematically networks and SOM require input vectors x_J=(x₁,x₂,x₃,.....x_JP) training weights w_l=(w_l1,w_l2,.....w_lp), where l indicates the number of nodes, W_lj denote the weights assigned to entry of nodeand is number input variables.where l indicates the number of nodes, lj w denote the weights assigned to entry j x of node l and p is number input variables One way to establish the structure of the SOM type neural network is shown in Figure 1, which indicates that the basic structure of the network must be input layer, hidden layer and output layer, the number of neurons in each layer is determined by the information processing capacity and robustness to want to project the problem, the problem presented in this work a static neural network is established with a number finite neurons, 20 neurons in each of the layers of the neural network.

Figure 1 Architecture basic neural network.

The distance between each of the nodes is made using the equation of Euclidean distance between the input nodes and the projection (bond lengths), Eq (1)

Where α denotes function of excitation each neuronal network, e error of propagation is training which should tend to zero, Nis total number of nodes in the neuron network. The use of batch mode training provides an accurate gradient vector, thus ensuring convergence to a local minimum, this basically does not happen with sequential training as BP because it becomes a search in the space of weights estimation stochastically, however the stochastic nature prevents convergence of the algorithm.

Results and discussions

The set of thermodynamic data obtained is listed in Table 1.The negative value of(Gibbs free energy) reflects the spontaneity of materials. Attractive interactions between 

Properties	IPN/CC
ΔG (kcal mol-1)	-4173.19
Log P	-1.87

Table 1 QSAR properties for composite

systems is the interaction between two or more molecules leading to self–organization by formation of a complex structure which has lower conformation equilibrium than of the separate components and shows different geometrical arrangement with high percentage of yield.¹⁹ Log P (graphene) indicates that the roughness effect in conjunction with the surface chemistry of the graphene sheets can be used to dramatically alter the wettability of the substrate. The hydrophilic graphene sheets are used (for example, by sonicating the as–produced graphene in water) the substrate acquires a super hydrophilic character.^20-22

Structural parameters

Computational analysis was carried out to determine the optimized geometry of graphene, PU, CC, respectively. Table 2 shows the results obtained by ANNs, as discussed the previous literature, the changes in frequency or bond length of the C–H bond on substitution is due to a change in the charge distribution on the carbon atom of the ring. The substitutes may be either of the electron withdrawing type (Cl, Br, F, etc.) or electron donating type (CH₃, C₂H₅, etc.). The reverse holds well on substitution with electron donating groups. The actual change in the C–H bond length would be influenced by the combined effects of the inductive–mesmerize interaction and the electric dipole field of the polar substitute. The calculated geometric parameters can be used as foundation to calculate the other parameters for the compound.²³

Bond	ANNs (Å)	Bond	ANNs (Å)	Bond	ANNs (Å)	Bond	ANNs (Å)
PU		Graphene				CC
O9=C8	1.157	C1-C2	1.4932	C28-C29	1.4951	1st mole
C8=N1	1.2193	C2-C3	1.4543	C29-C30	1.5338	Ca1-O2	2.383
N1-C2	1.4581	C3-C4	1.4546	C30-C16	1.4933	O3-C4	1.4284
C2-C3	1.6203	C4-C5	1.4546	C25-C24	1.4551	C4-O2	1.4284
C3-C4	1.5394	C5-C6	1.4929	C24-C23	1.4518	O2-Ca1	2.383
C4-C5	1.6067	C6-C1	1.5338	C23-C22	1.4571	C4=O5	1.2176
C5-C6	1.6201	C4-C7	1.4568	C22-C13	1.4577
C6-C7	1.6228	C7-10	1.4568	C22-C21	1.4557	2nd mole
C7-N10	1.5247	C10-C9	1.4546	C21-C20	1.4557	Ca1-O2	2.383
N10-C11	1.4288	C9-C8	1.4921	C20-C19	1.4578	O3-C4	1.4284
C11=O13	1.2276	C8-C5	1.4921	C20-C32	1.4571	C4-O2	1.4284
C11-O12	1.3713	C10-C17	1.4545	C32-C31	1.4517	O2-Ca1	2.383
O12-C15	1.4051	C17-C16	1.4543	C31-C28	1.4551	C4=O5	1.2176
C15-C16	1.6301	C16-C15	1.4932	C24-C40	1.4943
C16-C17	1.6083	C15-C14	1.5338	C40-C39	1.5346	3rd mole
C17-C18	1.5384	C14-C9	1.4929	C39-C38	1.5345	Ca1-O2	2.383
C18-C19	1.6044	C2-C27	1.4933	C38-C37	1.4921	O3-C4	1.4284
C19-C20	1.6077	C27-C26	1.5337	C37-C23	1.4526	C4-O2	1.4285
C20-O21	1.4043	C26-C25	1.4947	C37-C36	1.4923	O2-Ca1	2.383
O21-C22	1.3658	C25-C12	1.4538	C36-C35	1.4923	C4=O5	1.2176
C22=O25	1.2272	C12-C3	1.4539	C35-C21	1.4554
C22-N23	1.4071	C12-C13	1.4566	C35-C34	1.4924
N23-C26	1.4506	C13-C11	1.456	C34-C33	1.4924
C26-C27	1.6533	C11-C7	1.4565	C33-C32	1.4526
C27-C28	1.822	C11-C19	1.456	C33-C43	1.4922
C28-C29	1.6525	C19-C18	1.4566	C43-C42	1.5349
C29-C30	1.5408	C18-C17	1.454	C42-C41	1.5349
C30-C31	1.6206	C18-C28	1.4539	C41-C31	1.4945
C31-N32	1.4582
N32=C33	1.2194
C33=O34	1.1571

Table 2 Comparation of structural parameters of graphene/PU/CC composite using PM3 and ANNs.

FTIR

Table 3 shows the FTIR results of absorption of CC in graphene/PU composite. The results show an appreciable difference of the different materials alone with respect to composite, indicating a strong interaction between the three materials.

Assignment	Frequency (cm-1)
CH2 symmetric vibrations (PU)	5380–5261, 4424–4040, 3304
C=N symmetric vibrations (PU)	3947, 3781–3709
NH (PU)	3709, 3394
CH2 symmetric, C=O vibrations (PU)	3518
C–C stretching (PU)	3209, 2219
C=C (Graphene)	3034, 2628, 2412
C–C (Graphene)	2805, 1948, 1315, 1026, 733
C=O (PU)	1735
C–N,O–C–O (PU)	2219, 1678, 1026
O–C–O (PU)	1678
C–O–Ca (CC)	1507, 934
C–N, C-O (PU)	611
Ca–H (CC–PU), C–H (Graphene–PU)	61

Table 3 FTIR result of graphene/PU/CC

Bands at around 2219, 1678 and 1026 1067 cm^-1 are originated from stretching of C–O–C and C–N bond in the PU. In addition, the peaks at 3518, 3034, 2628, 2412, 1735, 1640, 1580 and 1060 cm^-1 can be assigned to the stretching vibration of carboxyl, carbonyl moiety of quinine, aromatic C=C bonds. The peaks at 5380–5261, 4424–4040, 3304 cm^-1 are related to the asymmetric and symmetric stretching vibrations of pendant methyl groups. Symmetric vibrations are generally weaker than asymmetric vibrations since the former lead to less of a change in dipole moment. Actually, during sonication it may graphene flakes are broken and this pendant methyl group came into sight.²⁴ The peaks at 2805, 1948, 1315 and 1026 cm^-1 shows C–C stretching of graphene. At 1735, 1507 and 934 cm^-1 appearance of new peaks which has been assigned to the vibration of carbonyl group is due to the formation of hydrogen bonds between CH groups of graphene and C=O of PU so, NH bond (PU) with C–O (CC), respectively.

Electrostatic potential

Figure 2 demonstrates the MESP of absorption process of CC in graphene/PU composite and their electrostatic interactions, showing the negative (red) regions were related to electrophilic reactivity and the positive (blue) regions to nucleophilic reactivity. The absorption of CC by the graphene/PU has mainly involved the formation of hydrogen bonds between PU and graphene and CC with PU respectively. The negative log P values for the graphene/PU indicated that absorption properties of the composite are dominated by its hydrophilic character and that absorption plays an important role in the CC absorption partitioning and receptor–binding. It was also shown that graphene changes the hydrophobicity of PU. The MESP values from 0.0837 at 0.067 eV indicated that the nucleophilic and electrophilic regions mainly involved the C=O, C–O of the PU and CC, respectively so graphene molecule, respectively.

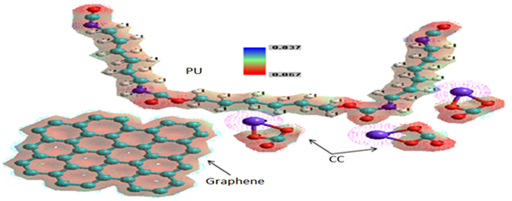
Figure 2 MESP of graphene/PU/CC, where: red color–oxygen, white color–hydrogen, light blue–carbon and dark blue–nitrogen atom, respectively.

Artificial Neuronal Networks (ANNs)

ANNs can be applied in the recognition of images, but not only are limited in that application; these also can be applied in the estimate or projection in the molecular simulation. The application of ANNs in molecular simulation is given by estimating possible formation of molecules this is achieved by applying the neural network SOM (Self -Organizing Map), which made ​​possible a projection of the molecule on a space in two dimensions (2-D). A demonstrated the interaction between PU and graphene is added a molecule of CC, to make the introduction of CC is observed between the molecule CC and PU interaction exists Figure 3, graphene remains the molecule with higher proportion of link between similar molecules graphene but still present interaction between the PU, the above is shown in the bond lengths between the PU and CC (Figure 4).

Figure 3 Simulation of absorption process of CC in PU/graphene composite.

Figure 4Simulation bond lengths of absorption process of CC in PU/graphene composite.

Conclusion

Acknowledgments

Conflicts of interest

References

©2016 Vazquez, et al. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.