Nanotechnology, a network of technologies, has achieved momentous precedence worldwide over last few decades. Progression in nanoparticle synthesis and nanoparticle based drug delivery systems is extensively anticipated to change the scenario of pharmaceutical industries because of the remarkable change in the properties of materials at nanoscale typically by virtue of their increased specific surface area to volume ratio and reactivity, which in principal may increase their biomedical applications. In the present study, a theoretical study has been carried out about nanostructures acting as nano capsules for drug delivery. A mathematical model has been formulated for the delivery and removal rate of nano capsules using a simple differential approach.

Nanotechnology, an interdisciplinary science that incorporates physics, chemistry, biology, etc. involves creation and utilization of materials, devices or systems on the nanometer scale and is currently undergoing unexpected development on many fronts. It finds numerous applications in material strengthening and fabrication, healthcare, agriculture, processing and storage of foods, robotics for human welfare, energy conservation and utilization, transport, manufacturing of safe and quality products and security at global level [1-11]. Besides, these unparalleled applications it has incredible potential for revolutionizing all fields of technology and is expected to create innovations and play a vital role in various biomedical applications like, drug delivery systems, molecular imaging, biomarkers, therapeutics, diagnostics, cancer therapy, biosensors, etc. Synthesis via benign route and building of orderly drug delivery systems are very important for medical and health-care. In this field, nano-based drug delivery system specifically nanoparticles have developed a great modification that provides new opportunities to move over hindrances and flaws of conventional drug delivery methods like enhance solubility of drugs, diminish drug toxicity, beshields drugs from deterioration, ineffective and benign delivery of drugs to specific target sites in the body, etc. [12-15].

In the present communication, a theoretical study has been carried out about nanostructures acting as nano capsules for targeting drugs to specific sites in the body in drug delivery systems without incorporating the effect of viscosity and friction of blood, gravity, and external guiding field. A mathematical model has been formulated for the delivery and removal rate of nano capsules using a simple differential approach.

In this section, we will try to find and solve the model for nano-particle injection (acting as nano capsules) into the blood stream of a patient. Let us assume that in the beginning i.e., at t = 0 a constant amount of A grams/min is injected into the blood stream of a patient. Upon reaching the target the removal of nano capsules is equally important in order to avoid the complications caused by their presence in the target body. Let us further assume that the nano-particles are simultaneously removed at a rate proportional to the amount of nano-particles present at time t [16-18]. Let y (t) represents the amount of nano-particles present at time t, then
$Remaval rate \propto y\left(t\right)$
$Remaval rate=ky\left(t\right)$
Where k is the constant of proportionality. Hence the model is, $y^{\prime }\left(t\right)=A-ky\left(t\right)$
Where $y\text{'}\left(t\right)=\frac{dy}{dt}$

In this section, we will try to analyze the results of mathematical model. Comparing it with $\frac{dy}{dt}+ Py=Q$ , whose solution is $y e^{{{\displaystyle \int }}^{\text{}}Pdt}= {{\displaystyle \int }}^{\text{}}Q{e}^{{{\displaystyle \int }}^{\text{}}Pdt}+ C$ , where P and Q are constants or functions of t. Here, P = k, Q = A and $e^{{{\displaystyle \int }}^{\text{}}Pdt}=e^{{{\displaystyle \int }}^{\text{}}kdt}$ we have
$y{e}^{{{\displaystyle \int }}^{\text{}}kdt}= {{\displaystyle \int }}^{\text{}}Q{e}^{{{\displaystyle \int }}^{\text{}}kdt}+ C$
$y{e}^{kt}= \raisebox{1ex}{$A{e}^{kt}$}\!\left/ \!\raisebox{-1ex}{$k$}\right.+ C$
$y= \raisebox{1ex}{$A$}\!\left/ \!\raisebox{-1ex}{$k$}\right.+ C{e}^{-kt}$
Imposing the boundary conditions, y(0) = 0, at t = 0 we have, $C= \raisebox{1ex}{$A$}\!\left/ \!\raisebox{-1ex}{$k$}\right.$ . Therefore, the level of the nanoparticles present in the blood stream of the patient at time t is given as
$y\left(t\right)= \raisebox{1ex}{$A\left(1- e^{-kt}\right)$}\!\left/ \!\raisebox{-1ex}{$k$}\right.$
Where A represents the amount of nanocapsules injected into the blood stream per minute. The removal rate is given as
$Removal rate\left(R\right)=ky= \raisebox{1ex}{$KA\left(1- e^{-kt}\right)$}\!\left/ \!\raisebox{-1ex}{$k$}\right.= A\left(1- e^{-kt}\right)$
Now, the ratio of level present (L) and the removal rate (R) is $\raisebox{1ex}{$L$}\!\left/ \!\raisebox{-1ex}{$R$}\right.= \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$k$}\right.$ , or $\raisebox{1ex}{$R$}\!\left/ \!\raisebox{-1ex}{$L$}\right.= k$ . The value of k will determine the behavior of level present and removal rate. Figure 1 shows the graphs between $\raisebox{1ex}{$L$}\!\left/ \!\raisebox{-1ex}{$R$}\right.=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$k$}\right.$ and $\raisebox{1ex}{$R$}\!\left/ \!\raisebox{-1ex}{$L$}\right.= k$ . It is clear that the value of k should be chosen in such a manner so that the removal rate of the nano capsules should be equivalent to the level present in the target body in order to avoid the complications created by its presence in the body.

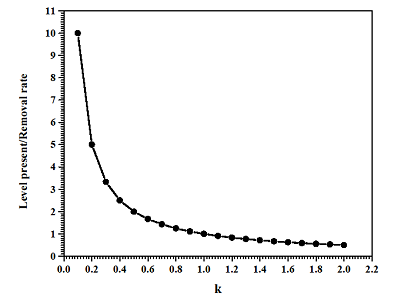
Figure 1: The graphs between $\raisebox{1ex}{$L$}\!\left/ \!\raisebox{-1ex}{$R$}\right.= \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$k$}\right.$ , and $\raisebox{1ex}{$R$}\!\left/ \!\raisebox{-1ex}{$L$}\right.= k$ .

In the present communication, a theoretical study has been carried out about nanostructures acting as nano capsules for targeting drugs to specific sites in the body in drug delivery systems without incorporating the effect of viscosity and friction of blood, gravity, and external guiding field. A mathematical model has been formulated for the delivery and removal rate of nanocapsules using a simple differential approach. It would be interesting to analyze the modeling results in terms of their connection with real parameters like viscosity and friction of blood, gravity and external guiding field.