We realized a virtual design of new azadipeptides nitriles (ADPNs) potential inhibitors of the cysteine protease falcipain 2 (FP2) protease inhibitors of Plasmodium falciparum (pf) by structure-based drug design (SBDD). From a series of 7 ADPNx with known FP2 inhibition potency, we constructed the FP2-ADPNx complexes by in situ modification of the X-rays crystal structure of FP2 in complex with epoxysuccinate E64 (pdb entry code: 3BPF). Out of then a one descriptor quantitative structure activity relationships (QSAR) model was built resulting in linear correlations between the gas phase computed enthalpy ∆∆H_MM upon the FP2-ADPN complex formation and IC₅₀^exp (R square of 0.88; cross validated R square of 0.86 ; F-Test of 39.48). Thereafter taking into account the solvent effect and the loss of vibrational entropy of the inhibitor upon binding to the enzyme led to an improved QSAR model correlating the computed Gibbs free energy (GFE: ΔΔG_com) of FP2-ADPN complex formation and IC₅₀^exp (R square of 0.94 ; cross validated R square of 0.94 ; F-Test of 91.44). The estimated IC₅₀^pred from FP2 inhibition pharmacophore model derived from the QSAR model linearly correlates with IC₅₀^exp (R square of 0.99) bearing in this way structural inhibition information that served in the virtual screening of a combinatorial subset of a virtual library (VL) of more than 8000 ADPNs analogues. From the ADME focused VL, 68 best hit fit orally bioavailable analogues were selected and finally in silico evaluated with the GFE QSAR model to identify new powerful ADPNs with predicted IC₅₀ reaching 0.5nM.

 Keywords: malaria, FP2, QSAR, pharmacophore, virtual screening, ADME

FP2/FP3, falcipain 2/falcipain 3; pf, plasmodium falciparum; ADPN, azadipeptide nitrile; SBDD, structure-based drug design; E64, epoxysuccinate; PDB, protein data bank; QSAR, quantitative structure activity relationships; ΔΔG_com, relative gibbs free energy change related to the enzyme-inhibitor complex formation; ΔΔH_MM, relative enthalpic contribution to the Gibbs free energy change derived by molecular mechanics; ΔΔTS_vib, relative entropic contribution of the inhibitor to the Gibbs free energy; ΔΔG_sol, the relative solvation Gibbs free energy contribution to the gibbs free energy change; GFE, gibbs free energy; IC₅₀^exp, experimental inhibition constant ; VL, virtual library; ADME, adsorption distribution metabolism and excretion; ACTs, artemisin-based therapies; E, enzyme; DS, discovery studio (molecular modeling program); MOE, molecular operating environment (molecular modeling program); I, inhibitor; E:I, enzyme–inhibitor complex; SAR, structure-activity relationship; MM, molecular mechanics; CFF91, consistent force field 91; eint, interaction energy; 2D/3D, Two dimension/three dimension; RMSD, root mean square deviation; PH4, pharmacophoric hypotheses four features; Hypo, hypotheses; Et/Met/Ph, ethyl/methyl/phenyl; HB, hydrogen bond; vdW, van der waals; HOA, human oral absorption; nM, nanomolar

Malaria is endemic all over the world and causes many deaths among populations, especially in the tropics, mainly in sub-Saharan Africa. It is one of the largest parasitic infections in the world and its incidence is estimated at 212 million clinical cases with a mortality rate of 429 thousand people of which more than 303 thousand are children under 5 years or 70% of cases.¹

This disease is caused by unicellular eukaryotic parasites of genus plasmodium. Of the five malaria parasites know to infect humans (falciparum, vivax, malariae, ovale and knowlesi), plasmodium falciparum is the most virulent.² One concern in the treatment of malaria is the spread of resistance to most available drugs. Chloroquine was one mainstay of antimalarial therapy. However, this drug is now inefficient against Plasmodium falciparum (Pf),³ and recently clinical treatments failures have been reported for other antimalarial drugs, including artemisi-nin combined therapies (ACTs).^4–6 Since resistance to a wide range of antimalarial drugs is spreading throughout “at parasite infection risk” populations worldwide and a protective vaccine remains unavailable,⁷ there is therefore urgent and imperative need to identify and develop novel classes of antimalarials. Plasmodium falciparum relies on hemoglobin hydrolysis to supply amino acids for protein synthesis and to maintain osmotic stability. Hemoglobin is transported to an acidic (pH 4-6) food vacuole, where it is hydrolyzed by multiple enzymes (E), including food vacuole cysteine, aspartic, and metalloproteases, before further action against hemoglobin fragments by a cytosolic aminopep-tidase.^8,9 Hemoglobin degradation is blocked by cysteine protease inhibitors (I), causing characteristic morphological abnormality in which the food vacuole is full of non-degraded hemoglobin blocking by this way parasite development.^10,11

The Pf genome contains 33 open reading frames predic-ted to encode cysteine proteases, including 4 cathepsin L-like papain family proteases collectively known as falcipains.¹² Falcipain-2 (FP2) and falcipain-3 (FP3) are key papain-family (C1) Clan CA trophozoite cysteine proteases localized in the digestive food vacuole that cleave host native or denatured human hemoglobin. FP2, the most-expressed and best-studied enzyme among falcipains, is a promising target for novel anti-malarial drugs development.¹³ Disruption of FP2 leads to marked reduction in hemoglobin hydrolysis by tropho-zoites, although this phenotype is transient.¹⁴ The main classes of FP2 inhibitors are peptides or peptido-mimetics bearing the most popular pharmacophores of cysteine protease inhibitors, such as vinyl sulfones, halomethyl ketones, and aldehydes. Furthermore, many other chemotypes have been identified as FP2 inhibitors, such as isoquinolines, thiosemicarbazones, and chalcones.¹⁵ Also peptide nitriles have drawn increasing attention in recent years as the cyano group gives rise to preferred interaction with the active site thiol by the formation of an enzyme-bound thioimidate that can result in potent enzyme inhibition.^16–18 The active site of FP2 is large and contains four pockets, S1, S’1, S2 and S3, each pocket accommo-dating one substituent, P1, P’1, P2 and P3 of peptide substrate. Thus, the scissile bond is localized between the residues P1’ and P1 of the peptide and a cut that minimizes the energy of complex (protein-substrate) is obtained when the remaining substituents, P2 and P3, fit together perfectly with the remaining pockets S2 and S3. Previous structure-activity relationships (SAR) studies highlighted that FP2 and related enzymes, react preferentially with peptidyl ligands containing large hydrophobic side chain at P2 position and, have a clear preference for substrate that contain a leucine (Leu) residue at this position rather than phenylalanine (Phe) or valine (Val). In fact, the fragments in position P2 provides the basis for the specificity of the peptide inhibitors and the S2 subsite reflects the key determinant of selectivity of FP2.¹⁹ Moreover, azadipeptide nitriles (ADPN) exhibit anti-malarial activity dependent on their structure and Reik Loser et al. reported the prominent role of the residue in P1 for development of this class of antimalarials.²⁰

The reported ADPN inhibitors activity (IC₅₀) range is very large: 59-50,001nM.²⁰. The availability of X-ray crystal structure of FP2 in complex with epoxysuccinate E64 (pdb code 3BPF to resolution 2.9Å), opened a gate to the structure-based design of novel potent antimalarial agents. In this work we start from a reduced series of 7 ADPN as a training set to construct a one descriptor (Gibbs free energy, GFE upon FP2-Inhibitor complex formation) QSAR model of FP2 inhibition, correlating GFE with experimental IC₅₀. Subsequently, a 3D-QSAR pharmacophore protocol was used to prepare a four-feature pharmacophore (PH4) model from FP2 active site bound ADPN conformations. This PH4's robustness due to the quality of FP2 inhibition structural information therein served to screen a virtual combina-torial library of ADPN analogues with the aim to design more potent orally bioavailable FP2 inhibitors.

The complexation methodology has been described largely according to a procedure successfully used to elaborate one descriptor QSAR models of viral, bacterial and protozoal enzyme-inhibitor complexes and to design from them peptidomimetic, hydroxynaphthoic, triclosan, thymidine, pyrrolidine carboxamide derivatives and peptide inhibitors.^21–31 The workflow below in Figure 1 describes the steps of whole process of virtual design of novel ADPN analogues.

Training sets

The chemical structures of the training set comprising the 7 ADPNs and the experimental biological activities (IC₅₀^exp) studied here are taken from the literature.²⁰ The IC₅₀^exp values ​​of these compounds cover a very wide concentration range (59 - 50,001nM) in order to build a reliable QSAR model.²⁰.

Model building and calculation of binding affinity

Simulations were carried out for the enzyme: inhibitor (FP2:ADPN) complexes, the free enzyme FP2 and the free ADPN inhibitor from the high-resolution 3BPF.pdb structure using Insight II molecular modeling program. Initially no molecules of crystallographic water were conserved in the molecular model, then the structures of the FP2 and FP2: ADPN complexes were at pH 7 with neutral N- and C-terminal and finally the protonable and ionizable residues of FP2 were loaded. Inhibitors were prepared from 3BPF.pdb by in situ modification of functional groups in the molecular scaffold of the endogenous E64 inhibitor. All rotatable bonds of the replacing fragments were subjected to an exhaustive conformational search coupled with careful gradual energy-minimization of the modified inhibitor and active-site FP2 residues located in the immediate vicinity (around 5Å radius) in order to identify low-energy bounded conformations of the modified inhibitor. The resulting low-energy structures of the entire FP2:ADPN complexes were then carefully refined by energy-minimization procedure the stable structure. The complete description of the complexation binding affinity (DG_com) is described in ref.³⁰:

ΔΔG_com=ΔG_com(I)−ΔG_com(I_ref)=ΔΔH_MM−ΔΔTS_vib+ΔΔG_sol (1).

ΔΔH_MM describes the relative enthalpic contribution to the GFE change related to the intermolecular interactions in E:I complex derived by molecular mechanics (MM), ΔΔG_sol and ΔΔTS_vib represent, respectively, the relative solvation GFE and simplified relative vibrational entropy.

Molecular mechanics (MM)

Simulations of the inhibitors and their complexes models were carried out with all-atom representation using atomic and charge parameters of the class II consistent force field CFF91.²⁷ A dielectric constant of 4 was used for all molecular mechanics (MM) calculations in order to take into account the dielectric shielding effect in proteins. Minimizations of the E:I complexes, free E and I were carried out by relaxing the structures gradually, starting with added hydrogen atoms, then with residue side chain heavy atoms and by the protein backbone relaxation. In all the geometry optimizations, a sufficient number of steepest descent and conjugate gradient iterative cycles were used with the convergence criterion for the average gradient set to 0.01kcal/molÅ⁻¹

Conformational search

Conformations of free inhibitors were obtained from the bound conformations in the binary E:I complexes by gradual relaxation to the nearest local energy minimum. Then a Monte Carlo search (≤50,000 iterations) for low-energy conformations was performed over all rotatable bonds, except those in the rings, using Discovery Studio 2.5 (DS 2.5) molecular modeling program.³² Two hundred unique inhibitor conformations were generated by randomly varying torsion angles of the last accepted conformer by ±15 deg at 5000K followed by subsequent energy minimization with a dielectric constant ε=80 to approximate the dielectric screening effect of solvation. The conformer with the lowest total energy was selected and re-minimized at a dielectric constant of 4.

Solvation Gibbs free energy

The electrostatic component of the solvation GFE which includes the effect of ionic strength via solving the nonlinear Poisson-Boltzmann (PB) equation^33,34 was computed by the DelPhi module of Discovery Studio.³². Here the solvent is a high dielectric constant (ε_o=80) continuous medium and the solute a low dielectric constant (ε_i=4) charge distribution filling a cavity with boundaries linked to the solute’s molecular surface. DelPhi numerically solves for the molecular electrostatic potential and reaction field around the solute using finite difference method on a (235×235×235) cubic lattice grid for the E:I complexes and free E and on (65×65×65) grid for the free I. Full coulombic boundary conditions were employed. Two subsequent focusing steps led to a similar final resolution of about 0.3Å per grid unit at 70% filling of the grid by the solute. Physiological ionic strength of 0.145mol·dm⁻³, atomic partial charges and radii defined in the CFF force field parameter set³² and a probe sphere radius of 1.4Å were used. The electrostatic component of the PB solvation GFE was calculated as the reaction field energy.^{26,29,34–36}

Interaction energy

The MM interaction energy (E_int) calculation protocol available in Discovery Studio 2.5³² was used to compute the non-bonded interactions (van der Waals and electrostatic interatomic potential terms) between two sets of atoms in the E:I complexes. All pairs of each FP2 residue–inhibitor interactions of the total enzyme-inhibitor E_int were evaluated using CFF force field parameters at ε=4.³² In particular, E_int breakdown into active-site residues contributions shows in the detail the strength and level of the main individual interactions, allowing in this way a quantitative identification of residues with highest contribution to the ligand binding affinity and suggests structural modifications in terms of inhibitor molecular moieties which carries the key features responsible for favorable binding affinity oy biological activity.²⁷

3D-QSAR pharmacophore (PH4) generation

PH4 modeling assumes that a set of key structural features responsible for compound biological activity is recognized by the active site during receptor binding. In this work the PH4 was prepared by the 3D-QSAR pharmacophore protocol of Catalyst HypoGen algorithm.³⁷ implemented in DS 2.5.³¹ Bound conformations of ADPNs taken from the refined E:I complexes were considered for the PH4 building. The top scoring PH4 hypothesis was prepared in three stages: constructive, subtractive and optimization step, from a set of most active ADPNs. The inactive compounds served for the definition of excluded volume. During the generation, five features available in the HypoGen algorithm were selected: hydrophobic aromatic (HYdAr), hydrophobic aliphatic (HYd), hydrogen-bond donor (HBD), hydrogen-bond acceptor (HBA), and ring aromatic (Ar) feature. Default values of the adjustable parameters were kept during the PH4 generation, except the uncertainty on the biological activity (IC₅₀), which was reduced to 1.25 instead of 3. This modification of the uncertainty interval of IC₅₀ from a wide span ⟨IC₅₀/3, 3·IC₅₀⟩ to a relatively narrow one ⟨4·IC₅₀/5, 5·IC₅₀/4⟩, is due to accuracy and homogeneity of the measured IC₅₀ originating from the same laboratory.²⁰ The top ten PH4 were generated with the number of missing features set to 0. Finally, the best PH4 model was selected. Generally a PH4 model, as the one described here, can be used to estimate the pIC₅₀ of new analogues on the basis of their mapping to its features. In this study, priority was given to the PH4 based screening of ADME focused virtual libraries (VLs).

ADME-related properties

Properties that determine the pharmacokinetics profile of a compound, besides octanol/water partitioning coefficient, aqueous solubility, blood/brain partition coefficient, Caco-2 cell permeability, serum protein binding, number of likely metabolic reactions and other eighteen descriptors related to adsorption, distribution, metabolism and excretion (ADME properties) of the inhibitors were computed by the QikProp program³⁸ based on the methods of Jorgensen.^39–41 According to those methods, experimental results of more than 710 compounds among which about 500 drugs and related heterocycles were correlated with computed physicochemical descriptors resulting in an accurate prediction of molecule’s pharmacokinetic profile. Drug likeness (#stars) is represented by the number of descriptors that exceed the range of values determined for 95% of known drugs out of 24 selected descriptors computed by the QikProp.³⁸ Drug-likeness was used as the global compound selection criterion related to ADME properties. The calculation of the selected ADME descriptors were performed from 3D structures of compounds considered. These descriptors were used to assess the pharmacokinetics profile of designed compounds and served also for the VL focusing.

Virtual combinatory library generation

The analogue model building was performed with Molecular Operating Environment (MOE) program.⁴² The library of analogues was enumerated by attaching R-groups (fragments, building blocks) onto ADPN scaffold using the Quasar CombiDesign module of MOE.⁴² Reagents and chemicals considered in this paper were selected from the directories of chemicals available from the commercial sources. Each analogue was built as a neutral molecule in the MOE program,⁴² its molecular geometry was refined by MM optimization through smart minimizer of DS³² at high convergence criteria (threshold on energy difference of 10⁻⁴kcal/mol and root mean square deviation (RMSD) of 10⁻⁵Å), ε=4, using class II consistent force field CFF.⁴³

ADME-based library focusing

Twenty four pharmacokinetics-related molecular des-criptors available in QikProp,³⁸ which characterize a wide spectrum of molecular properties as described in §2.8, Optimum ranges of these 24 descriptors were defined in terms of upper and lower bounds according to QikProp.³⁸ Only compounds with predicted drug-likeness (#stars, Section 2.8) equal to zero, were retained in the focused VL of drug-like ADPN analogues.

 Pharmacophore based library focusing

The PH4model described in Section 2.7 was derived from the bound conformations of ADPNs at the active-site of FP2. The enumerated and ADME-focused VL was further focused by using the ligand pharmacophore mapping protocol available of Discovery Studio.³² Within this protocol, each generated conformer of the analogues was geometry optimized by means of the CFF force field for a maximum of 500 energy minimization steps and subsequently aligned and mapped to the PH4 model in order to select the top ranking overlaps. Twenty best-fitting inhibitor conformers were saved and clustered into 10 conformational families according to their mutual RMSD by Jarvis-Patrick complete linkage clustering method.⁴⁴ The best representative of each cluster was considered in the virtual screening of analogues. Only those analogues mapping to all four PH4 features were retained for the in silico screening.

 In Silico screening

The conformer with the best mapping on the PH4 in each cluster of the focused library subset was selected for in silico screening by the complexation QSAR model. The relative GFE of E:I complex formation in water ΔΔG_com was computed for each selected new ADPN analogue and then used for prediction of FP2 inhibitory potencies (IC₅₀^pre) of the focused VL by inserting this parameter into the pfFP2 receptor target-specific scoring function: pIC₅₀^pre=a·ΔΔG_com+b (2).

A series of 7 azadipeptide nitriles (ADPN) and their experimental activity (IC₅₀^exp) from the same laboratory²⁰ were selected and presented in Table 1. Their IC₅₀^exp covering a very wide range of activity of 59 to 50 001nM allowed to build a reliable QSAR model.

The relative GFE upon (E:I) complex formation ΔΔ𝐺_com was calculated for the FP2-DNAPx complexes as described in § Method. Table 2 shows GFE and its components, eq. (1). ΔΔ𝐺_com reflects the mutual affinity between the enzyme and the inhibitor. Since it’s calculated with an approximate approach the relevance of the binding model is evaluated by a linear regression, eq. (2) analysis which led to a linear correlation with experimental activity data (IC₅₀^exp,²⁰). Two correlation equations obtained for the GFE ΔΔG_com, eq. (B) and its enthalpic component ΔΔH_MM, eq. (A) are presented in Table 2 with the relevant statistical data. The relatively high values ​​of the regression coefficient R² and the Fischer F-test of the correlation involving ΔΔG_com, eq. (B), Table 3, indicate a strong relationship between the binding model and the experimental inhibitory potency IC₅₀^exp of the series of ADPN as plotted in Figure 2.

ADPN 6-7

The ADPN’s active conformation from this QSAR is revealed in Figure 3, (Figure 4) (Figure 5) (Table 4) for the most active ADPN2. Subsequently the enzyme–inhibitor intermolecular interaction energy breakdown to the active site pockets key residues are listed in Table 4 with their correlation with experimental activity (IC₅₀^exp) plotted in Figure 4. A comparative individual residue contribution between the most active ADPN2 and the less active ADPN7 confirms the observed IC₅₀^exp trend.

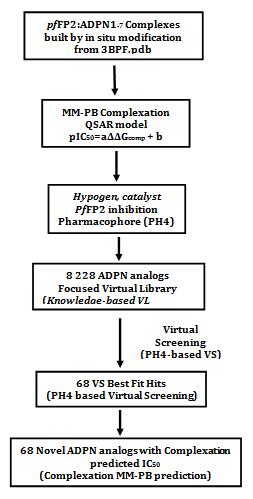
Figure 1 Multistep approach workflow to virtually design novel ADPN analogs with higher predicted potency against FP2.

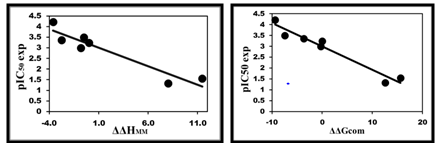
Figure 2 (Left): Plot of correlation equation between pIC₅₀ and relative enthalpic contribution to the GFE (eq. (A)) ΔΔH_MM; (Right) Similar plot for relative complexation GFE (eq. (B)) ΔΔG_com of the training set, all in kcal·mol⁻¹.

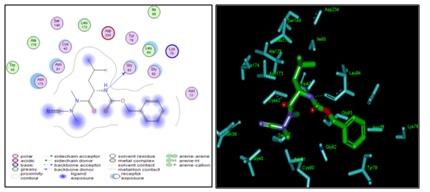
Figure 3 (Left) 2D schematic interaction diagram of the most potent inhibitor ADPN2 (Table 1) at pfFP2 active-site; (Right) 3D structure of the active-site with bound inhibitor ADPN2.

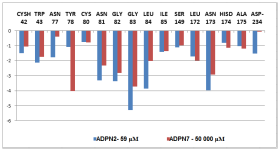
Figure 4 Plot of the correlation between active site key residues Cysh42, Trp43, Ser149, Asp-234, Gly82, Gly83, P2 and P1P2 and S2 contribution to E_int of pfFP2-ADPNx.

The FP2 inhibitory pharmacophore (PH4) model elaborated from the QSAR model is presented in Table 5 & Table 6, Figure 6. The 3D-QSAR PH4 generation was carried out in three steps: the constructive, the subtractive and the optimization step (§ Method). During the constructive phase of HypoGen the most active ADPNs for which IC₅₀^exp ≤2x59nM, were automatically selected as the leads. Thus, the most active ADPN2 (IC₅₀^exp=59nM) alone was used to generate the starting PH4 features and those matching this lead, were retained. During the subsequent subtractive phase, features which were present in more than half of the inactive ADPNs were removed. The PH4 which contained all features were retained. None of the training set compounds was found to be inactive (IC₅₀^exp>59x10^3, nM=186574.3nM). During the final optimization phase, the score of the PH4 hypotheses was improved. Hypotheses are scored via simulated annealing approach according to errors in the activity estimates from regression and complexity. At the optimization end, 10 best scoring unique hypotheses (Table 5) displaying four features were kept. The reliability of the generated PH4 models was then assessed using the calculated cost parameters ranging from 26.6(Hypo1) to 29.9(Hypo10). Their statistical data (costs, root-mean-square deviation RMSD, R²) are listed in Table 6, 0.353 ≤RMSD ≤0.801 and 0.98 ≤R² ≤0.99. The PH4 hypo1, with the best RMSD and highest R² was retained for further analysis; its regression equation pIC₅₀^exp=0.9926.pIC₅₀^pre+0.0527 (plotted in Figure 6), R² and R²xv greater than 0.9 and F-test of 1272.8 attest the predictive capacity of the PH4.

The Hypo1 fixed cost (26.2), lower than the null (127.0) by ∆=100.8, is a chief indicator of the PH4 model predictability (∆>70 corresponds to a probability higher than 90% that the model represents a valid correlation).¹⁶ The difference ∆≥97.1 for the set of 10 hypotheses confirms high quality of the pharmacophore model. The best-selected hypothesis Hypo1 represents with a probability of 98% a PH4 model with a similar level of predictive power as the complexation GFE enzyme-inhibitor binding QSAR model.

We have built a virtual library (VL) of new azadipeptide nitriles compounds with a variety of substitutions in positions P1, P2 and of the nitrogen adjacent to the cyano group with the goal to identify more potent orally bioavailable inhibitors of the pfFP2. They have been synthetized following a previously published protocol.¹² During the VL enumeration the R-groups listed in Table 7 were attached to positions R1–R3 of the ADPN scaffold to form a combinatorial library of the size: R1xR2xR3=44x17x11=8 228 analogues. In order to match the substitution pattern of the best training set inhibitor ADPN2 and to take into account the reported structural information about P1 and P2 position that is suitable for substitutions²⁰ and not excluded through the Lipinski’s rule violation (molecular weight >500g.mol^-1).¹⁷ In search of more focused library with increased content of drug-like and orally bioavailable molecules, we have introduced a set of filters and penalties, which can help to select smaller number of suitable ADPNs that will undergo in silico screening. The initial VL was thus filtered in an ADME-based focusing step to remove compounds with expected poor oral bioavailability and low drug-likeness. Only those with high predicted percentage of human oral absorption (HOA) in the gastrointestinal tract larger than 80%^19,20 and compounds satisfying the Lipinski’s rule of five¹⁷ computed for the entire virtual library using QikProp software,²¹ were kept.

From the set of 3023 analogs derived from Lipinski test, 93 of them were mapped to 4 features of the pharmacophore. Out of then, only 68 best fitting analogues (PH4 hits) have been retained and submitted to screening with help of the complexation QSAR model. Computed GFE of complex formation with FP2 of Pf and its component as well as predicted half-maximal inhibitory concentrations IC₅₀^pred estimated from the correlation Equation (B), Table 3. For the majority of new ADPN analogues, the estimated inhibitory potencies shown in Table 8 are better than that for the most active training set compound ADPN2 (IC₅₀^exp=59nM).²⁰

In order to identify which substituents (Table 7) lead to new inhibitor candidates with the highest predicted potencies towards the FP2 of Pf, we have prepared histograms of the frequency of occurrence of R1, R2 and R3 groups in the 68 PH4 best fitting hit ADPNs selected from the focused virtual library shown in Table 8 (Figure 7). From the histograms in Figure 7 it comes out that R1 groups numbered

11(20),13(4),14(4),15(4),19(4),20(4),21(4),22(4) and 23(4) are almost equally represented with the highest occurrence in the ADPNs subset. The R2 groups contain preferentially 42(25), 48(20), 49(4) and 50(5), 36(3) while the R3 groups include chiefly fragments 60(26), 61(28) and 70(12).

^afragments 1– 42 and 62* and 64* were also used in R1-groups; fragments 43–59 were used in R2-group and fragments 60–70 were used in R3-groups; ^bdashed bonds indicates the attachment points of individual fragments.

Figure 5 Molecular mechanics intermolecular interaction energy Eint breakdown (in kcal.mol-1) to residue contributions for ADPN2 and ADPN7, Table 2.²⁰

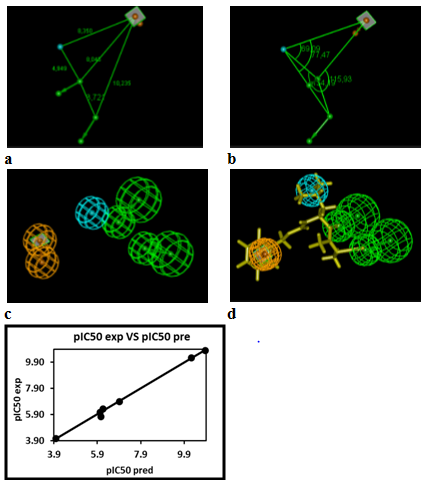
Figure 6 Coordinates (a,b), features (c) and mapping (d) of the FP2 inhibitor pharmacophore with the best training set ADPN2 (yellow). The correlation plot of experimental vs. predicted inhibitory activity is displayed above. The features are colored blue for hydrophobic aliphatic (HYd), green for hydrogen-bond acceptor (HBA), purple for hydrogen-bond donor (HBD) and orange for Aromatic (Ar). The arrows represent the projection for donor and acceptor features.

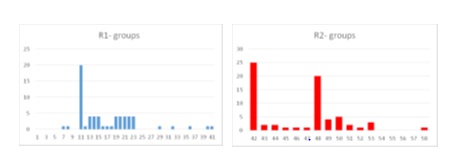
Figure 7 Histograms of frequency of occurrence of individual R1, R2-groups in the 68 best-selected analogues mapping to the four features of the PH4 pharmacophore hypothesis Hypo1 (for fragments structures Table 7).

From a reduced series of 7 ADPN as training set a one descriptor (FP2-ADPN1-7 complex formation GFE: ΔΔ𝐺_com) QSAR model of FP2 inhibition (pIC₅₀=f(ΔΔ𝐺_com)) was built revealing the ADPN active conformation. Then a 3D-QSAR pharmacophore (PH4) model of FP2 inhibition of bound ADPN conformations was elaborated. The PH4's predictability served to screen a virtual combinatorial library of ADPN analogues with the aim to design more potent orally bioavailable FP2 inhibitors.

The most important findings are first the likeness of the constructed active conformation of the ADPN1-7 from the complexation QSAR model and second the accuracy of the subsequent PH4’s IC₅₀ estimation as plotted in Figure 6. Overall this confirms the structural hypothesis according to which the inhibitory activity of structure-based designed similar ADPNs sharing the binding mode of the training set ADPN1-7 will be predicted suitably by the QSAR regression equation (B) and cross checked by the PH4 regression equation (C).

QSAR model

The robustness of this one descriptor QSAR model is assessed through the components of GFE (ΔΔ𝐺_com) namely the enthalpic ΔΔH_MM, solvation ΔΔG_solv and the loss of vibrational entropy upon the ADPN binding ΔΔTS_vib. The relevance of the enthalpic contribution to GFE is well confirmed by the quality of the regression indicating that in gas phase a large part (some 88%) of the variation of the IC₅₀ is explained by that of H_MM. Adding to H_MM the solvation contribution in order to come closer to the biological medium, kept the level of strong relationship between the experimental data and the simulation results. Finally the likeliness of the model is increased by the loss of the inhibitor vibrational entropy TS_vib to explain some 94% of the variation of IC₅₀ by that of GFE. This last contribution is one of the most reliable indicators of the predictive power of the QSAR model as reported by Freire et al.⁴⁵ For this reason the lack of validation set (VS), due to the small number of provided ADPNs experimental values is not detrimental, because the validation of the QSAR model is much more performed through the high predictive quality of the PH4 model derived from it than the VS, provided that it’s based on the bound conformation of the ADPNs (Figure 6 & Table 6). Therefore, the correlation equation (B) and computed ∆∆G_comp quantities can be used for prediction of inhibitory potencies IC₅₀^pred against pfFP2 for novel ADPN analogues respectively, since they share the same binding mode as their corresponding training set.

Binding mode of inhibitors

Beside the robustness of the QSAR model, the analysis of the interactions between ADPNs and FP2 is expected to reveal key interactions justifying ADPNx: FP2 affinity such as hydrogen bonds (HBs), van der Waals (vdW), hydrophobic contacts, etc. As displayed in Figure 3, the binding mode of ADPNs at FP2 active site of the best active ADPN 2 in 2D and 3D is supported by the following interactions: HB with Gly83 and Leu84 and hydrophobic contacts. In order to verify whether other interesting interactions not displayed have to be taken into account in the description of ADPN binding mode at FP2 active site for the design of new analogues, interaction energy (E_int) between each active site residue and ADPNx is computed (Table 4). The peptidyl structure of ADPN shed light on the structural features for binding affinity and opened the gate to the design of FP2 inhibitors taking benefit from S1 to S3 pockets filling. In this way key residues from these pockets contribution to the global interaction energy FP2–ADPNx correlate with their inhibitory potencies as displayed in Figure 4. S2 pocket filling exemplifies the overall impact for FP2 inhibition as reported¹³ previously. Oppositely Figure 5 displaying comparative contribution of each active site residue to E_int for the most active training set ADPN2 and the less active ADPN7 confirm the observed IC₅₀^exp trend but cannot justify the large gap in their inhibitory potencies. However in a recent work we succeeded in justifying the observed 37.5% jump in experimental biological activity between methylphosphonic arginine and hydroxamic acid derivative Pf Leucyl aminopeptidase (pfA-M17) inhibitors by the enzyme active site residues contribution to E_int at a level of 35%.⁴⁶ Therefore the essential structural information in the design of novel potent ADPN analogues will not be derived from E_int but from a more predictive descriptor. They will be selected, according to the workflow (Figure 1), by virtual screening from a diverse Virtual Library of analogues with the S2 hydrophobic contact as the central structural requirement displayed by the Pharmacophore model of FP2 inhibition provided by the one descriptor (GFE) QSAR model (Table 3) (Figure 2).

Analysis of new inhibitors from in Silico screening

The top scoring virtual hits are ADPN analogues: 15-48-61 (0.5nM), 22-48-61 (0.5nM), 24-48-61 (0.5nM), 19-48-61 (0.74nM), 22-59-61 (0.67nM), 14-59-61 (0.77nM), 20-48-61 (0.83nM) and 13-59-61 (0.9 nM) display predicted potency about one hundred times that of the best training set ADPN2. Albeit this exaggeratedly optimistic result, it suggests alternative suitable sidechains (different from current amino acid ones) for pockets filling. As we can see from Figure 8 the 3D interaction depiction (Top) of one of the best designed analogues 15-48-61 with FP2 and the Connolly surface of the binding site (Bottom), the n-pentyl (P1) of the training set is extended to n-pentyl hydroxyl while the benzyloxy is conserved in P3 for all the designed analogues mimicking the training set P3. The lipophilic S2 pocket accommodates a bulkier 1-ethyl-2-Me-C₆H₁₁(15) in place of the cyclohexyl moiety leading to an increase of hydrophobic contact equivalent to a better stabilization and greater affinity. These results are in agreement with reported structural information from experimental Structure - Activity Relationship (SAR) on FP2 and FP3 pyrimidine-carbonitrile inhibitors⁴⁷ and Complexation QSAR based in silico design of dipeptide nitriles inhibitors of FP3;³¹ they attest the accuracy of the FP2 pharmacophore derived from the one descriptor complexation QSAR model of FP2 inhibition by ADPNs.

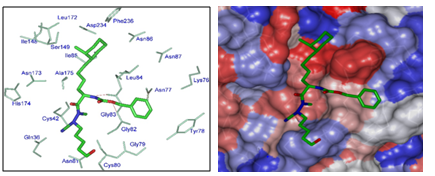
Figure 8 (Left) Close up of virtual hit 15-48-61 at the active-site of FP2. (Right) Connolly surface of the active-site of FP2 of Pf with bound predicted most active ADPN inhibitor 15-48-61. The binding site surface is colored according to residue hydrophobicity: red—hydrophobic, blue—hydrophilic, and white—intermediate.

The ADME-related properties described in Section 3.9 were computed. The values for the best active designed ADPNs were compared with those computed for drugs used for treatment of malaria or currently undergoing clinical trials. Most of the best designed analogues ADPNs are predicted to display good level of druglikeness as well as high human oral absorption in the gastrointestinal tract (HOA).

The structure-based design of pfFP2 inhibitors has been attempted with various scaffolds. The main strategy remains the increase of hydrophobic enzyme – ligand contact.⁴⁸ Due to the lack of quantitative accurate structural information about the pfFP2 active site subpockets efforts were oriented towards SAR studies of peptides and non peptidic scaffolds^49,50 but so far no integrated approach combining 3D-QSAR, PH4 and in silico screening has been reported and useful structural information is provided here.

Assessment to FP2 inhibition key structural information either from crystal structure of FP2-ADPNx complex or in situ modification of an existing FP2-Generic Inhibitor as in this work is a reliable way to design potent, orally bioavailable and favorable pharmacokinetic ADPN antimalarials. From the short training set of Reik Löser et al.²⁰ despite the low diversity of the substitutions at P1, P2 and P3, a one descriptor QSAR model correlating the computed Gibbs free energy upon complex formation with the experimental enzyme inhibitory potency shed light on the main interactions impacting activity. Deriving a 3D QSAR Pharmacophore (PH4) model of FP2 inhibition from active conformations of ADPNs at the enzyme active site taking into account the inhibitor loss of entropy upon binding increased the robustness of the PH4 in order to screen virtual libraries (VL) of ADPNs analogues. The design strategy based on the hydrophobic contact at S2 pocket in the best 3D QSAR PH4 model generated since the P3 Aromatic moiety was conserved for all ADPNs. The PH4 selected VL subset of ADPN analogues of 68 was crossed with the GFE computation of predicted inhibitory potencies (Table 3, Equation B). The best designed analogues 15-48-61 (0.5nM), 22-48-61 (0.5nM), 24-48-61 (0.5nM), 19-48-61 (0.74nM), 22-59-61 (0.67nM), 14-59-61 (0.77nM), 20-48-61 (0.83nM) and 13-59-61 (0.93nM) in the low nanomolar range (Table 8) are recommended for synthesis and activity evaluation to check the consistency of the structural information provided in order to guide in the future discovery of non-peptide or peptidomimetic FP2 inhibitors.

This work was also supported by the Slovak Research and Development Agency grants APVV-14-0294 and APVV-15-0111".

The authors declare there is no conflict of interest in relation with the work presented herein.

1. World Malaria Report 2016: Summary. Geneva: World Health Organization; 2017.
2. Vythilingam I, Noor Azian Y, T Huat, et al. Plasmodium Knowlesi in humans, macaques and mosquitoes in peninsular Malaysia. Parasit vector. 2006;1(1):26
3. Hyde JE. Drug–resistant malaria–an insight. FEBS J. 2007;274(18):4688–4698.
4. Wongsrichanalai C, Meshnick SR. Declining artesunate–mefloquine efficacy against falciparum malaria on the Cambodia–Thailand border. Emerg Infect Dis. 2008;14(5):716–719.
5. Dondorp AM, Nosten F, Yi P, et al. Artemisinin resistance in Plasmodium falciparum malaria. Eng J Med. 2009;361(15):455–467.
6. Garcia Linares GE, Rodriguez JB. Current Status and Progresses Made in Malaria Chemotherapy. Curr Med Chem. 2007;14(3): 289–314.
7. Juliane Wunderlich, Petra Rohrbach, John Pius Dalton. The malaria digestive vacuole.Front Biosci. 2012;4:1424–1448.
8. Francis SE, Sullivan DJ, Goldberg DE. Hemoglobin metabolism in the malaria parasite Plasmodium falciparum. Annu Rev Microbiol. 1997;51:97–123.
9. Rosenthal PJ. Protease Inhibitors. In: Antiparasitic Chemotherapy: Mechanisms of Action, Resistance, and New Directions in Drug Discovery. New York: Springer; 2001:325–345.
10. Rosenthal PJ, McKerrow JH, Aikawa M, et al. A malarial cysteine proteinase is necessary for hemoglobin degradation by Plasmodium falciparum. J Clin Invest. 1988;82(5):1560–1566.
11. Gamboa de Dominguez N D, Rosenthal PJ. Cysteine proteinase inhibitors block early steps in hemoglobin degradation by cultured malaria parasites. Blood. 1996;87:4448–4454.
12. Iain D Kerr, Ji H Lee, Kailash C Pandey, et al. Structures of Falcipain–2 and Falcipain–3 Bound to Small Molecule Inhibitors: Implications for Substrate Specificity. J Med Chem. 2009;52(3):852–857.
13. Boris D Bekono, Fidele Ntie–Kang, Luc COO, et al. Targeting cysteine proteases from Plasmodium falciparum: A general overview, rational drug design and computational approaches for drug discovery. Curr Drug Targets. 201819(5):501–526.
14. Rosenthal PJ. Cysteine proteases of malaria parasites. Int J Parasitol. 2004;34(13–14):1489–1499.
15. Ettari R, Bova F, Zappala M, et al. Falcipain–2 inhibitors. Medicinal Research Reviews. 2010;30(1):136–167.
16. Moon JB, Coleman RS, Hanzlik RP. J Am Chem Soc. 1986;108:1350.
17. Ward YD, Thomson DS, Frye LL, et al. Design and synthesis of dipeptide nitriles as reversible and potent Cathepsin S inhibitors. J Med Chem. 2003;45(25):5471–5482.
18. Löser R, Schilling K, Dimmig E, et al. Interaction of papain-like cysteine proteases with dipeptide-derived nitriles. J Med Chem. 2005;48(24):7688–7707.
19. Shenai BR, Lee BJ, Alvarez–Hernandez A, et al. Structure–activity relationships for inhibition of cysteine protease activity and development of Plasmodium falciparum by peptidyl vinyl sulfones. Antimicrob Agents Chemother. 2003;47(1):154–160.
20. Reik Löser , Jiri Gut, Philip J. et al. Antimalarial activity of azadipeptide nitriles. Bioorganic & Medicinal Chemistry Letters. 2010;20(1):252–255.
21. Frecer V, Kabelac M, De Nardi P, et al. Structure–based design of inhibitors of NS3 serine protease of hepatitis C virus. J Mol Graph Model. 2004;22(3):209–220.
22. Frecer V, Jedinak A, Tossi A, et al. Structure Based Design of Inhibitors of Aspartic Protease of HIV–1. Letters in Drug Design & Discovery. 2005;2(8):638–646.
23. Frecer V, Berti F, Benedetti F, et al. Design of peptidomimetic inhibitors of aspartic protease of HIV–1 containing –Phe Psi Pro– core and displaying favourable ADME–related properties. J Mol Graph Model. 2008;27(3):376–387.
24. Dali B, Keita M, Megnassan E, et al. Insight into selectivity of peptidomimetic inhibitors with modified statine core for plasmepsin II of Plasmodium falciparum over human cathepsin D. Chem Biol Drug Des. 2012;79(4):411–430.
25. Megnassan E, Keita M, Bieri C, et al. Design of novel dihydroxynaphthoic acid inhibitors of Plasmodium falciparum lactate dehydrogenase. Med Chem. 2012;8(5):970–984.
26. Owono Owono LC, Keita M, Megnassan E, et al. Design of Thymidine Analogues Targeting Thymidilate Kinase of Mycobacterium tuberculosis. Tuberc Res Treat. 2013;670836.
27. Keita M, Kumar A, Dali B, et al. Quantitative structure–activity relationships and design of thymine–like inhibitors of thymidine monophosphate kinase of Mycobacterium tuberculosis with favourable pharmacokinetic profiles. RSC Advances. 2014;4(99):55853–55866.
28. Frecer V, Seneci P, Miertus S. Computer–assisted combinatorial design of bicyclic thymidine analogs as inhibitors of Mycobacterium tuberculosis thymidine monophosphate kinase. J Comput Aided Mol Des. 2011;25(1):31–49.
29. Owono Owono LC, Ntie–Kang F, Keita M, et al. Virtually Designed Triclosan–Based Inhibitors of Enoyl–Acyl Carrier Protein Reductase of Mycobacterium tuberculosis and of Plasmodium falciparum. Mol Inform. 2015;34(5):292–307.
30. Kouassi AF, Kone M, Keita M, et al. Computer–Aided Design of Orally Bioavailable Pyrrolidine Carboxamide Inhibitors of Enoyl–Acyl Carrier Protein Reductase of Mycobacterium tuberculosis with Favorable Pharmacokinetic Profiles. Int J Mol Sci. 2015;16(12):29744–29771.
31. Esmel A, Keita M, Megnassan E, et al. Insight into binding mode of nitrile inhibitors of Plasmodium falciparum Falcipain–3, QSAR and Pharmacophore models, virtual design of new analogues with favorable pharmacokinetic profiles. J Comput Chem Molec Model. 2017;2–1:1–21.
32. Discovery Studio Molecular Modeling and Simulation Software. USA: San Diego; 2009.
33. Gilson MK, Honig B. The inclusion of electrostatic hydration energies in molecular mechanics calculations. J Comput Aided Mol Des. 1991;5(1):5–20.
34. Rocchia W, Sridharan S, Nicholls A, et al. Rapid grid–based construction of the molecular surface and the use of induced surface charge to calculate reaction field energies: Applications to the molecular systems and geometric objects. J Comput Chem. 2002;23(1):128–137.
35. Böttcher CJF, Bordewijk P. Theory of electric polarization. 2nd edition. The Netherlands: Elsevier; 1973.
36. Miertuš S, Scrocco E, Tomasi J. Electrostatic interaction of a solute with a continuum. A direct utilizaion of ab initio molecular potentials for the prevision of solvent effects. Chemical Physics. 1981;55(1):117–129.
37. Li H, Sutter J, Hoffmann R. Pharmacophore Perception, Development and Use in Drug Design. In: Güner OF, editor. USA: CA; 2000:171–189.
38. Schrodinger Software. New York: Schrodinger, USA; 2014.
39. Duffy EM, Jorgensen WL. Prediction of properties from simulations: Free energies of solvation in hexadecane, octanol, and water. J Am Chem Soc. 2000;122:2878–2888.
40. Jorgensen WL, Duffy EM. Prediction of drug solubility from Monte Carlo simulations. Bioorg Med Chem Lett. 2000;10(11):1155–1158.
41. Jorgensen WL, Duffy EM. Prediction of drug solubility from structure. Adv Drug Deliv Rev. 2002;54(3):355–366.
42. https://www.chemcomp.com/MOE-Molecular_Operating_Environment.htm
43. Maple JR, Hwang MJ, Stockfisch TP, et al. Derivation of class II force fields. I. Methodology and quantum force field for the alkyl functional group and alkane molecules. J Comput Chem. 1994;15(2):62–182.
44. Willett P. Molecular Similarity in Drug Design. Glasgow, UK: Chapman and Hall; 1994:110–137.
45. Freire E. Do enthalpy and entropy distinguish first in class from best in class? Drug Discov Today. 2008;13(19-20):869–874.
46. N'Guessan H, Megnassan E. In silico Design of Phosphonic Arginine and Hydroxamic Acid Inhibitors of Plasmodium falciparum M17 Leucyl Aminopeptidase with Favorable Pharmacokinetic Profile. J Drug Design Med Chem. 2017;3(6):98–125.
47. Cotereon JM, Catterick D, Castro J, et al. Falcipain Inhibitors: Optimization Studies of the 2–Pyrimidine–carbonitrile Lead Series. J Med Chem. 2010;53(16):6129–6152.
48. Tiwari HK, Kumar P, Kumar K, et al. In Vitro Antimalarial Evaluation of Piperidine– and Piperazine–Based Chalcones: Inhibition of Falcipain–2 and Plasmepsin II Hemoglobinases Activities from Plasmodium falciparum. Chemistry Select. 2017;2(25):7684–7690.
49. Himangini, Dharam Pal Pathak, Vidushi Sharma, et al. Designing novel inhibitors against falcipain–2 of Plasmodium falciparum. Bioorg Med Chem Lett. 28(9):1566–1569.
50. David J Weldon, Falgun Shah, Amar Chittiboyina, et al. Synthesis, biological evaluation, hydration site thermodynamics, and chemical reactivity analysis of α–keto substituted peptidomimetics for the inhibition of Plasmodium falciparum. Bioorg Med Chem Lett. 24:1274–1279.