In the 1950’s, the research findings of James Watson, Francis Crick, Rosalind Franklin, and Maurice Wilkins led to the discovery of the deoxyribonucleic acid (DNA) double-helix conformation.^1,2 With DNA at their core, many nucleic acid based assays are used in pharmaceutical, biochemistry, biotechnology, molecular biology, target-based drug design, and other DNA-based technologies.^3-7 In addition, DNA is the molecular target of numerous anti-tumor drugs, anti-viral drugs, and several anti-bacterial agents.^8-10 Historically there have been several approaches in developing some pharmacological and therapeutic agents that interfere with DNA synthesis.^8,11 Since the therapeutic effects of many DNA-binding interactions correlate with thermodynamic profiles of the resulting complexes, elucidation of thermodynamic parameters of such interactions are important in nucleic acid-based therapeutics.^12,13

Differential Scanning Calorimetry (DSC), which provides unique complementary information for nucleic acids, modified nucleic acids, and nucleic acid-ligand interactions, is a powerful method in obtaining thermodynamic parameters. DSC is a direct, model-independent measurement tool that complements, structural and bonding information obtained by various physicochemical methods.^13-15 This review is designed to give the reader a greater understanding of the applications of DSC in DNA-based therapeutics. While this review focuses on calorimetry studies of DNA-based complexes, DSC applications in RNAs have been reviewed elsewhere.^16-18

Keywords: calorimetry, biomolecules, denaturation, drugs, hybridization, thermodynamics

DSC, differential scanning calorimetry; ITC, isothermal titration calorimetry; dsDNA, double stranded deoxyribonucleic acid; ssDNA, single stranded deoxyribonucleic acid; RNA, ribonucleic acid; H-C, helix-coil; MBs, molecular beacons; LNAs, locked nucleic acids; PCR, polymerase chain reaction

In this review, commonly used terms and their meanings are presented as follows: (1) A ligand (natural and synthetic) is used loosely to cover any molecule (substrate, inhibitor, drug, cofactor, prosthetic group, metal ion, protein, nucleic acid, probe, target, and modified nucleic acid) that non-covalently binds to a second molecule.^10,19 DNA-Ligand interaction is also used loosely to refer to the following: DNA-DNA, DNA-RNA, DNA-Protein, DNA-Lipid, DNA-Drug, and DNA-Biological macromolecule binding reactions. (2) The quantities ΔG, ΔH, ΔS, and ΔC рrefer to the universal Gibbs free energy change, standard enthalpy change, standard entropy change, and heat capacity change, respectively.

These are also called “thermodynamic profiles”. (3) Under standard conditions (1.00 M concentration of reactants and pro­ducts, temperature of 25°C, 1.00 atmosphere pressure, and pH of 7.0), these are designated ΔG°, ΔH°, and ΔS°, respectively. The reported calorimetric thermodynamic values obtained from DSC melting experiments are designated $\Delta G_{cal}$ , $\Delta H_{cal}$ and $\Delta S_{cal}$ respecti­vely. The overall calorimetric free energies,$\Delta G_{cal}$ are determined from the following Gibb’s equation:

$\Delta G_{cal}(T)=\Delta H_{cal}-T\Delta S_{cal}$   (1)

where, T is the Kelvin temperature, and R is the universal gas constant with values of 1.98 cal mol⁻¹ K⁻¹ or 8.315 J mol^-1 K^-1.

Nucleic acids are polynucleotides that include DNA, RNA, and various modifications. At the cellular level, gene expression has distinct roles for DNA and RNA during transcription and translation. Generally, DNA has three major functions in a cell:^2,20

1. To serve as a permanent repository of genetic information.
2. To replicate during cell division.
3. To serve as a template for gene expression transactions.

With DNA at its core, the field of nucleic acid therapeutics has evolved considerably with numerous gene targets applied in vitro and in vivo in a variety of contexts and with varying degrees of success.^11,21 In particular, DNA oligonucleotides²² have been used in a wide range of applications, from diagnostics⁷ and therapeutics,¹⁷ to nanotechnology.²³ According to Bellini et al.,²⁰ studies of nucleic acid-based binding transitions have been gradually improving in recent years. In fact, since the completion of the Human Genome Project (HGP) around 2003 the demand for molecular diagnostic assays in medicine and biotechnology has increased.

Emerging biotechnological applications of DNA and RNA hybridization-based technologies (e.g. DNA microarrays, DNA-based biopharmaceuticals, PCR, anti-gene targeting, RNA interference, and molecular beacon assays), have also heightened the need to optimize and standardize the underlying chemical reactions.^4,24 Design and construction of nucleic acid-ligands with tunable, structural and hybridization properties have recently been topics of intense research.^24,25 Based on accurate predictions of thermodynamic stability, nucleic acid-based alignment routines are employed to optimize probe-primer design strategies for PCR based applications, locked nucleic acids (LNA),²⁶ DNA-protein complexes²⁷ and other nucleic acid based therapeutic systems.⁷

This review focuses on applications of DSC on nucleic acid-based therapies and delivery systems. These include, but are not limited to: DNA-DNA, Drug-DNA transactions, DNA-protein, and DNA-ligand interactions. DSC analysis provides direct, model-independent evaluations of the thermodynamic profiles of biological samples. This review begins with a summary of the stabilizing forces in nucleic acids, especially DNA and RNA. Next, a brief discussion of the structure of nucleic acids is followed by a description of DSC instrumentation used to obtain model-independent, thermodynamic profiles. The review also discusses the crystal structure of the B-form of double stranded DNA (dsDNA),²⁰ and the Nearest-Neighbor (NN) model²⁸ used for predicting DNA stability.²⁹

The Helix-to-Coil (H-C) transition models,^30,31 and nucleic acid hybridization phenomena in simplex versus multiplex environments²⁵ are also discussed. Beyond this point, the principles of ITC and DSC are briefly reviewed together with the basic thermodynamic formalism. Because nucleic acids and their modifications are common targets for anti-cancer, antibiotic, and other anti-viral drugs, a discussion of nucleic acid-ligand interactions is made. The applications of DSC in modified nucleic acids, nucleic acid-ligand binding, drug binding, probe-target reactions, and nucleic acid hybridization routines are discussed in the context of nucleic acid-based therapeutics and some DNA delivery systems. Finally, the case is made for more DSC research on nucleic acid-based molecular biomarkers that detect most diseases through multiplexed, high-throughput techniques and other thermally induced detection methods.

DNA duplex stability, stabilizing forces and thermodynamics

Advances in the interdisciplinary science of biophysics have led to detailed knowledge of DNA and its interactions with other biological systems.³² The structure and thermodynamic stability of a variety of DNA duplexes depends on a fine balance of interactions¹ and slight variations can have profound implications on propagation of genetic information to future generations. As shown on schematic diagram in Figure 1, the DNA duplex stability is attributed to several forces:^29,33,34 (1) base pairing hydrogen bonds (H-bonds) between complementary bases on opposite strands, two H-bonds between Adenine-Thymine (A-T), and three H-bonds between Guanine-Cytosine (G-C) bases, (2) base-stacking , van der Waals forces and hydrophobic interactions between stacked bases, (3) various interactions with the solvent environment, and (4) electronic interactions between phosphates along the helix backbone.²⁰

Figure 1 The B form of the double helix structure of DNA, with its important dimensions and the main interactions.²⁰

Generally, thermodynamic studies of DNA are focused on determining the combined value of stacking and pairing in the overall ΔG. This subtle balance of molecular constraints and interaction forces all compete and play a role in the biological processes.²⁴ The thermodynamic profiles generated from DSC can be used to calculate the stability and predict the temperature-dependent behavior of any DNA sequence.¹⁶ A schematic diagram showing the secondary structure of DNA, commonly called the double helix is shown in Figure 1.

Figure 1 shows that DNA and RNA consists of the following components in their structure:² (1) a pentose sugar, (2) a heterocyclic organic base (purine and pyrimidine), linked by specific hydrogen bonding interactions, and (3) a negatively charged phosphate moiety. The orientation of the strands is from the 5’-end to the 3’-end, anti parallel in opposite directions.

By convention, nucleic acid sequences are written from left to right, from the 5’-end to the 3’-end. The W/C A-T and C-G ratio is constant (Chargaff’ rule). The B-form is the most biologically prevalent DNA helix geometry.^20,34 This is characterized by a shallow, wide major groove and a deep, narrow minor groove, while strand backbones are closer together on one side of the helix than on the other. Other forms of DNA are the A-DNA and Z-DNA and these are described elsewhere.³⁴

Although this review focuses on DSC applications in DNA-based assays, RNA applications are discussed briefly herein. The primary structure of RNA is generally a long, single-stranded polynucleotide regulatory molecule, serving as an intermediary on the pathway to protein production in a cell.² Functionally different forms of RNA exist including: (1) messenger (mRNA), which is synthesized from DNA and encodes for protein production, (2) transfer (tRNA), which functions as an adaptor between mRNA and amino acid codons, (3) ribosomal (rRNA), which serves as a major structural component of ribosomes, and (4) non-coding RNAs, which are discussed in detail elsewhere.³⁵

RNA stability can be manipulated thus, modulating gene expression.³² RNA also serves as the genetic material for most viruses, including HIV,³⁶ while other RNA molecules are enzymes with catalytic activity (e.g. ribozymes). RNA interference (RNAi) technology is a powerful molecular biology laboratory tool to study and manipulate gene function.¹¹ Small interfering RNAs (siRNAs) provide new opportunities for the development of new therapeutics in human disease therapies.^2,21

Major and minor grooves in DNA and ligand binding

Specific interactions between proteins and DNA are fundamental to many biological processes.^12,27 The potential utility of DNA recognition in molecular life sciences, medicine, as well as in the pharmaceutical industry.^3,37 makes it a target for the diagnosis and treatment of human diseases.¹² DNA is the major target of most drugs, and depending on the mode of interaction, these drugs can be classified into these four broad categories: (1) intercalating agents, (2) groove-binding agents, (3) covalent bonding agents, and (4) strand-breaking agents.¹⁰ These can interfere with double stranded DNA (dsDNA) and single stranded DNA (ssDNA) chemical structure, thus interfering with DNA replication and transcription. A detailed account of the origins of specificity in protein-DNA recognition processes and the role of DNA shape in protein-DNA recognition has been reviewed elsewhere.^12,37 The sugar phosphate backbone of paired strands defines the helical grooves, within which the edges of the heterocyclic bases are exposed.

Helix-coil transition in DNA other biomolecules

Processing of genes into nucleic acids and proteins is a substantial goal in molecular medicine, and DNA is the medium of information storage.² An important feature of most biological associations, including DNA, is its reversibility.³⁸ The process of gene expression is dependent upon the localized opening of the dsDNA in order to expose the ssDNA during the transcription process.³⁸ The DNA molecule forms helical structures in their active form (dsDNA) and melt to a random coil phase (ssDNA) in their denatured form.³⁹ The denaturation process consists of a H-C transition that can be achieved by denaturing agents (e.g. chemicals, enzymes or heat), and the models of this H-C phenomena have been published by many authors.^31,39,40 The dsDNA helix can be reversibly melted when heated above a certain temperature to separate the complementary strands into a random coil conformation (Figure 2). Denaturation is followed by a change in the physical properties of DNA. As the double stranded DNA denatures, there is a sharp increase in heat capacity $(\Delta C_P)$ due to the duplex unwinding being an endothermic process (hyperchromic effect), and a reproducible melting curve is observed for DNA.¹

Figure 2 Melting and hybridization in DNA.

Utility of UV visible spectroscopy in nucleic acid-based therapeutics

First, it is noted that the absorbance increases when the DNA duplex is denatured, a phenomenon called hyperchromicity.^1,2 Denaturation (melting) transition is caused by heating in the laboratory, or by denaturing agents in the body. On the other hand, renaturation (re-association) is an annealing process, which involves cooling the reaction below the melting temperature of DNA and is both sequence and salt dependent. However, understanding the energetics of dsDNA duplexes requires accurately predicting the overall values of ΔG, ΔH, and ΔS, as well as Tm for each specific sequence. Generally, thermodynamic parameters for DNA hybridization are sequence-dependent.^33,41

DSC and ITC are used in conjunction with some other spectroscopic techniques like Ultraviolet-visible (UV/VIS) spectrophotometry and fluorescence spectroscopy to characterize the biological binding interactions. A brief review of the three techniques will be made, followed by a detailed discussion of the DSC.

1. Ultraviolet-visible (UV/VIS) spectrophotometry: In short, spectroscopy is the study of the interaction of electromagnetic radiation with matter, and is used to investigate the internal structure of atoms and biological molecules by analyzing absorption spectra.¹ In relation to nucleic acids, all purine and pyrimidine bases have substantial aromatic character due to delocalized π orbital electrons. A typical UV absorption spectrum of DNA shows a characteristic absorbance peak at a wavelength of 260 nanometers (A₂₆₀). Optical density (OD), and absorbance are sometimes used interchangeably for nucleic acids, thus:

$A=log(Io/I)$   (2a)

where A represents absorbance of the sample, I_o is the intensity of light that is incident on the sample, and I is the intensity of light that is transmitted through the sample. The absorbance, A is typically measured in a 1.0 cm path length cell, and is related to the extinction coefficient and sample concentration through the Beer-Lambert law, represented by:

$A_{260}=Log\left(\frac{I_o}{I}\right)=\epsilon L\left[C\right]$   (2b)

1. where A₂₆₀ is the OD at 260 nm and ε is the molar-extinction coefficient of the DNA sample [L/(mol.cm)]. The quantities, I₀ and I are, respectively, the intensities of incident and transmitted light. The letter L represents the path length of the light through the sample (cm), and [C] is the molar concentration (mol/L) of the DNA species in different topologies. The molar extinction coefficient is a physical constant that is unique for each sequence and describes the A₂₆₀ of 1.0 mol/L. Evaluation of thermodynamic parameters from UV-absorbance melting curves inherently assumes a two-state model, and conventional UV/VIS spectrophotometry usually lacks sufficient sensitivity to detect subtle influences of the melting buffer.^1,2
2. Isothermal Titration Calorimetry (ITC) is another powerful and important technique for the study of the thermodynamics of macromolecular interactions whereby two reactants are titrated against one another and the extent of binding is determined by direct measurement of heat exchange.⁴² In general, thermodynamic profiles of biomolecules in aqueous solutions are derived from equilibrium-constant expressions at different temperatures. These can be association constants, K_a, or dissociation constants, K_d, as well as Van’t Hoff plots.¹⁹ Typically, in a single ITC experiment, ΔG of binding, ΔH, ΔS, and the binding constant (K_b), can be directly and accurately determined.⁴³
3. Lastly, and the primary experimental technique reviewed throughout this paper, is the DSC. DSC is a thermodynamic tool for the direct assessment of the heat energy uptake, which occurs in a biological sample within a regulated range of temperature change.^13,44 DSC measures the partial heat capacity, of a biological sample and reference (buffer), thus providing a ratio of the amount of energy absorbed by a sample as the temperature is increased or decreased. DSC provides qualitative and quantitative information about physical and chemical changes associated with nucleic acid conformational transitions, including a direct measurement of  $\Delta C_p^{ex}$ versus T. Additionally, DSC provides a direct measurement of the melting thermodynamics without invoking a model of the transition, (i.e. model-independent parameter evaluation).¹⁴

Thermodynamics of DNA melting and the nearest neighbor (NN) model

Historically, DNA double helix formation occurs in two steps: (1) helix initiation, followed by, (2) helix growth, or the propagation step.^31,40 Currently, DNA double helix formation is known to be comprised of the following three steps:^24,29,41 (1) the bringing of the single strands into spatial proximity (largely determined by the strand concentration, salt concentration and solvent viscosity), (2) the formation of the ‘nucleated’ complex, which begins with helix initiation, followed by nucleus formation, and lastly, (3) the ‘zippering’ of the dsDNA helix, also known as the propagation step.²⁴

Nucleic acid-based hybridization reactions utilize probe-target binding reactions⁴⁶ where the ability to predict how binding events will affect the thermodynamics of duplex formation is of utmost importance.²⁵ To date, the most widely applied and reliable thermodynamic calculations underlying the prediction of short-DNA duplex stability are based on the NN model.^20,24,29,41 The NN formalism is also widely used to investigate RNA folding.¹⁸ If accurately parameterized, the NN model can provide relatively accurate predictions of the sequence-dependent, thermodynamic stability of short nucleic acids.²⁹

According to the NN model, the overall ΔG of helix melting can be partitioned into three terms (SantaLucia & Hicks, 2004):

1. ΔG for the helix initiation, or nucleation step.
2. ΔG for helix propagation, which is the sum of the appropriate NN parameters for the particular NN doublets present in the duplex.
3. ΔG associated with the reduced entropy that occurs when the duplex is composed of two self-complementary single strands. The stability of a DNA double helix is estimated as the weighted sum of the stabilities when the 10 published W/C, NN base pair doublets are combined,^29,33,41 and is represented by the following equation:

$\Delta G_{duplex}^0=\Delta G_{initiaion}^0+{\displaystyle {\sum }_i{n}_i\Delta G_{i,i+1}^0}+\Delta G_{symmetry}^0$   (3)

where

$\Delta G_{initiaion}^0$ is the free energy change for the 10 possible W/C base pairs, $n_i$ is the number of occurrences of each NN, i, and $\Delta G_{initiaion}^0$ is termed the initiation (or nucleation) free energy for the duplex formation, which is considered unfavorable.$\Delta G_{initiaion}^0$ is assigned to account for the relative difficulty of forming the first W/C base pair (a thermodynamic entropy term) and a thermodynamically favorable “nucleation”of the remaining base pairs.²⁹ Sequence-independent effects, including those associated with counter ions, are included in this term. The term $\Delta G_{symmetry}^0$  is a symmetry correction free energy that accounts for the degeneracy in self-complementary versus non-self-complementary sequences.^20,29 In order to account for stability differences between DNA duplexes with terminal A-T versus G-C base pairs, two initiation parameters have been introduced, and a statistical thermodynamics formalism was introduced and discussed in detail.²⁹

DNA based binding interactions in drug design strategies

Virtually, all biological phenomena depend on some sort of molecular recognition in one way or another,¹⁴ and this is fundamental to the molecular functioning of living matter.⁴² The functions of many biomolecules involve reversible binding and generally, biochemical reactions are associated with large changes in enthalpy because of the large bond energies involved. Each functional group in a biomolecule has a finite size or steric dimension that contributes to the three-dimensional conformation of a given biological macromolecule.² Generally, the binding of a biological molecule to a ligand is often coupled to a conformational change, an important aspect in nucleic acid-based assays and drug design strategies. The quantitative description of the forces that govern the formation of biomolecular complexes is also part of the overarching goals of this review.

Proteins and nucleic acids behave cooperatively as they undergo structural rearrangements during binding reactions in solution because they are surrounded by solvent, among other factors. Rational development of new drugs, vaccines, and other nucleic acid-based compounds require understanding of the binding role of different functional groups interactions that influence both the pharmacokinetic and pharmacodynamic properties of drugs.^2,27 These include: (1) hydrophobic interactions, (2) hydrophilic interactions, (3) dipole-dipole interactions, (4) Coulombic forces, and (5) ion-dipole interactions. DSC is a powerful analytical tool, capable of elucidating the factors that contribute to the folding and stability of biomolecules.²⁷

Differential scanning calorimetry (DSC) theory

A calorimeter was one of the first scientific instruments reported in early literature, and biological calorimetry started from the pioneering work of Lavoisier and Laplace in the 1780s, who used the “ice calorimeter” to monitor heat release by animals.⁴⁷ Calorimetry was also developed by Black and his coworkers in the 1800s.⁴⁸ Calorimetry is designed to measure the difference in heat flow rate to a material (biological sample) and to a reference material (buffer) while they are subjected to a controlled temperature program.⁴² DSC is designed to directly measure the amount of heat energy absorbed or released by the biological sample as it is heated or cooled at a constant rate or held under isothermal conditions.

Monitoring the rate of the heat produced or consumed and obtaining thermodynamic profiles of the resultant thermally-induced phase transitions is the major goal of calorimetry. In a scanning calorimeter, one measures the specific heat of a system as a function of the temperature.¹⁷ When a biological sample is subjected to a linear temperature program, the heat flow rate into the sample is proportional to its instantaneous specific heat, and this has universal applicability in routine laboratory analysis. The three methods of calorimetric measurement are: (1) temperature change, (2) power compensation (often called isothermal), and (3) heat conduction.^13,17

Phase transitions are monitored by DSC and differential thermal analysis (DTA) techniques. For this review, broadly, DSCs will be classified into two types: (1) Heat-Flux DSCs and (2) Power-Compensated DSCs.⁴⁴ In a power-compensated DSC, the sample and reference pans are placed in separate furnaces heated by separate heaters (Figure 3). The sample and reference are maintained at the same temperature, and the difference in thermal power required to maintain them at the same temperature is measured and plotted as a function of temperature or time.⁴⁴

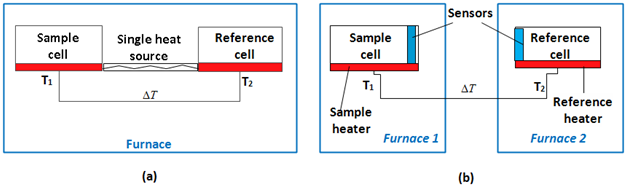
Figure 3 In a Heat-flux DSCs, the sample and reference are enclosed in the same furnace and the difference in energy required to maintain them at a nearly identical temperature is provided by the heat changes in the sample. (b) In Power-Compensated DSCs, the temperatures of the sample and reference are controlled independently using separate, identical furnaces and the temperatures of the sample and reference are made identical by varying the power input to the two furnaces.

In a heat flux DSC, the sample material, enclosed in a pan, is placed with an empty reference pan on a thermoelectric disk surrounded by a furnace. In the adiabatic heat flux method, power is determined by measuring the temperature difference across a thermal resistance.⁴⁵ The furnace is heated at a linear constant rate, and the heat is transferred to the sample and reference compartments through the thermoelectric disk. For a macromolecular sample heated at a constant rate, the heat capacity of the sample is compared to that of an exactly equal volume of buffer (Figure 3).

 In a typical DSC experiment, energy is introduced simultaneously into a sample cell (which contains a biological sample under study) and a reference cell (containing only the buffer), and the temperatures of both cells are raised identically over time.⁴⁵ Operation of the CSC Model 6100 Nano II-Differential Scanning Calorimeter (formerly Calorimetry Sciences Corporation, now TA Instruments, USA) is described below.^24,49

Briefly, the operating procedure is as follows:^24,49

1. The thermal jacket is heated and cooled at a constant rate.
2. The temperature of the jacket is controlled by the computer, using a known reference voltage.
3. The temperature of the control circuit then compares the reference voltage to that of the thermometer inside the calorimeter.?
4. After comparison, the computer controls the temperature of the jacket by adjusting the power applied to the heating and cooling elements through digital to analog converters, and then generates the raw melting curves (Figure 4).

Figure 4 Representative calorimetric melting curve for the raw buffer versus buffer scan.

Heat is supplied at the same rate to the two matched cells, and the following steps are taken to convert heat flow into excess heat capacity. The sample cell will generally absorb more heat than the reference cell, causing a slight difference in the temperature, $\left(\Delta T=T_2-T_1\right)$ between the two identical cells. A feedback loop monitoring temperature supplies a small amount of heat, $q_p$ to the solution cell, so as to equalize the temperatures. To obtain excess heat capacity, the raw voltages are converted to power, $\frac{d{q}_p}{dt}$ by the following equation(s):

$\left(\frac{d{q}_p}{dt}\right)=Heatflowrate$   (4)

Where $q_p$ is the rate of heat absorbed at constant pressure,⁴⁹ and

$\left(\frac{dT}{dt}\right)=Rateoftemperaturechange$   (5)

Generally $C_P$ ,refers to the ability of material to store heat and originates from the disruption of the forces stabilizing native biological structure. As noted in the previous section, these are vander Waals forces, hydrophobic interactions, electrostatic interactions, hydrogen bonds, hydration of exposed residues, pH, buffer, and ionic strength).⁴⁴ The $C_P$ at constant pressure is a temperature derivative of the enthalpy function, i.e.  $C_P=\Delta H/\Delta T$  at constant pressure.⁴²The power data is then converted to molar $\Delta C_P$ , via the following transformation:

$\left(\frac{d{q}_p}{dt}\right)/\left(\frac{dT}{dt}\right)=\left(\frac{d{q}_p}{dt}\right)=C_P$   (6)

The average excess heat capacity is a derivative from the average enthalpy, $\Delta H$ , at constant pressure. Finally, $\Delta C_P^{ex}$ , is calculated as follows:

$\Delta C_P^{ex}=\left(\frac{d{q}_p}{dt}\right)\left(\frac{1}{\sigma M}\right)$   (7)

Where σ = scan rate,$\frac{dT}{dt}$ and M= number of moles of the sample. The ΔH and ΔS of the induced melting transitions of duplex DNAs are evaluated from $\Delta C_P^{ex}$ versus T measurements, acquired as melting curves of the samples provided by DSC. In a DSC melting curve experiment the $\Delta C_P^{ex}$ is continuously monitored over a selected temperature range. The instrument utilizes a two cell design and electronic comparison scheme to determine $\Delta C_P^{ex}$ of the sample as it is heated.

An example of a typical DSC melting curve obtained from DNA-DNA sample

DSC and DNA–DNA hybridization studies

The function and capacity of DNA as the repository of genetic information depends on the physical properties of its molecular structure and stability.²⁴ The equilibrium formation of dsDNA from ssDNA is central to molecular diagnostics and biotechnology applications.^16,20 There are several important parameters in performing DSC on nucleic acids and their derivatives,⁴⁴ including: (1) buffers: the most common ones contain phosphate, acetate, and citrate which have minimal temperature dependence, (2)salt concentration: higher cationic concentrations generally lead to greater thermal stability of nucleic acids, and (3) length dependency: enthalpy of a nucleic acid depends on its length and base sequence where generally, the enthalpy decreases with the shortening of the nucleic acid fragment length.

In the DNA-DNA experiments reviewed below, the buffer used in the melting experiments contained combinations of sodium phosphate [NaH₂PO₄ (monobasic) and Na₂HPO₄ (dibasic)], respectively. The buffer changes in pKa with temperature are known to be small during the course of a melting experiment.²⁴ Additionally, the enthalpy of ionization, $\Delta H_{ion}$ , and heat capacity changes for buffer ionization are small, and the pH is relatively constant as temperature is varied.²⁴ Disodium ethylene diamine tetra acetic acid (Na2EDTA) was added to chelate trace metals and multivalent cations that could bind to the DNA and possibly cause damage or influence the melting process. The [Na+] of melting buffers were independently verified by taking electrical conductivity (K) measurements.

Examples of data analysis of DNA-DNA duplexes performed on a typical DSC

Analysis of DSC melting data reported below was performed using the proprietary software packages supplied by the manufacturer for use with the DSC instrument (DSC Run Software and Cp Calc 2.1 Software). A fundamental method is the use of a buffer-versus-buffer baseline to correct sample-versus-buffer scans by the way of a subtraction of the baseline from the average sample scan.²⁴ The result is a baseline-corrected $\Delta C_P^{ex}$ versus temperature curve, normalized for total biological molecule concentration, molecular mass, and cell volume.

To calculate the thermodynamic parameters of the resultant standardized, baseline-corrected curve, a progressive polynomial line is fit to connect linear regions in the lowest and highest temperature portions of the curve. Employing the temperature dependencies of the melting and binding enthalpies of nucleic acid transitions, the expression for the $\Delta C_P^{ex}$ upon nucleic acid complex melting transition is written in terms of the calorimetric melting enthalpy as shown in Equation 8 below. Integration of the area under the baseline-corrected DSC curve provides a measurement of the calorimetric transition enthalpy, $\Delta H_{cal}$ . As shown in Figure 5, the total integrated area below the thermo gram peak indicates total heat energy uptake by the biological sample after any effect to the transition is corrected, thus:

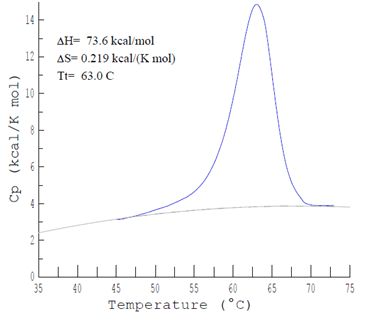
Figure 5a A typical tracing of the DSC curve observed with a solution perfectly matched DNA molecule scanned from 0°C to 110°C. DNA concentration was 1.05 mg/ml, pH 7.30, 0.085M sodium phosphate [NaH₂PO₄ (monobasic) and Na₂HPO₄ (dibasic)], respectively.

Figure 5b Schematic representation of the average $\Delta C_P^{ex}$ , obtained from DSC using a quadratic polynomial fit. As shown,$\Delta C_P^{ex}$ vs T values sometimes incur some uncertainty in measurements because of the subjective process of assigning pre-and post-transition baselines for some samples.

$\Delta H_{cal}={\displaystyle \underset{T_2}{\overset{T_1}{\int }}\Delta C_P(T)dT}$   (8)

Where T1 and T2are the beginning and ending temperatures of the DSC melting curve,respectively, defining the temperature range examined. Individual temperature integration ranges varied and are chosen to provide a line of best fit to the linear regions around the melting curve as seen when using the integration algorithm. The calorimetric entropy,$\Delta S_{cal}$ , is determined as follows:

$\Delta S_{cal}={\displaystyle \underset{T_2}{\overset{T_1}{\int }}\frac{\Delta C_P(T)}{T}}dT$   (9)

Reported values of the calorimetric free-energy,$\Delta G_{cal}(T)$ , are determined at a particular temperature. For example, at T = 298 K by the Gibb’s relation, this becomes:

$\Delta G_{298k}=\Delta H_{cal}-T\Delta S_{cal}$   (10)

A negative magnitude of ΔG represents higher stability of the native nucleic acid conformation relative to the denatured state, while amore negative ΔG represents greater stability. These thermodynamic parameters $\Delta H_{cal}$, $\Delta S_{cal}$ , and $\Delta G_{cal}(T)$ are evaluated from the equations described above. The analysis follows the standard assumption that the overall difference in $\Delta C_P^{ex}$ from the beginning to the end of the melting transition is negligibly small, (i.e.$\Delta C_P\left(T_2\right)-\Delta C_P\left(T_1\right)=0$

The validity of this assumption comes from the analysis of variations between the evaluated $\Delta H_{cal}$ and $\Delta S_{cal}$ with the $T_m$ for the molecules. The consequence of the assumption of negligible melting transition is that evaluated thermodynamic parameters are most accurate in the transition region, and more importantly, these parameters are assumed to be temperature-independent.

In the analysis reviewed herein, it is assumed in all cases that the melting transition occurs in an all-or-none, two-state, manner. The $T_m$ of a DNA oligo nucleotide duplex refers to the temperature at which half of the molecules are in their melted, single (unfolded) strand form, and half the molecules are in their duplex, or annealed state (folded).^29,45 Generally, $T_m$  is an indicator of thermos stability, and, generally, the higher the $T_m$ , the more thermodynamically stable the biomolecule.³¹ The $T_m$ can be taken as the temperature at the peak-height maximum on the corrected baseline, $\Delta C_P^{ex}$ versus temperature curve (Figure 5a). This temperature at the peak height maximum can expressed in terms of the $\Delta H_{cal}$ and $\Delta S_{cal}$ through the following expression:

$T_m=\left(\frac{\Delta H_{cal}}{\Delta S_{cal}}\right)$   (11)

In particular, for DNA, the following relationship is true:

$T_m^{-1}=R/\Delta H^0\ln \left(C_T/\alpha \right)+\Delta S^0/\Delta H^0$   (12)

Where for self-complementary sequences α =1, for non-self-complementary sequences α  = 4, and $C_T$ is the DNA strand concentration.⁵⁰

A plot of $T_m$ versus N is shown in Figure 6b, and which clearly shows that DNAs is increasingly stabilized with increases in [Na+]. Furthermore, values for $T_m$ increased with increasing DNA length. Low [Na+] and N, binding thermodynamic parameters for short DNAs were very weak and phosphate-phosphate repulsive forces dominate the electrostatic interactions. Salt-nucleic acid interactions were reviewed elsewhere and for improved predictions of $T_m$ , the reader is referred to.⁵⁰ In their study, values were systematically studied for a set of 92 DNA duplexes in a variety of [Na+] concentrations ranging from 0.069 M to 1.02 M, and the relationship between $T_m$ and ln [Na+] was found to be nonlinear (Figure 5).

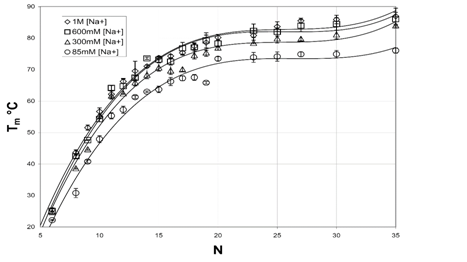
Figure 6 Plot of versus incremental DNA base pairs (N) for selected DNA duplexes.²⁴

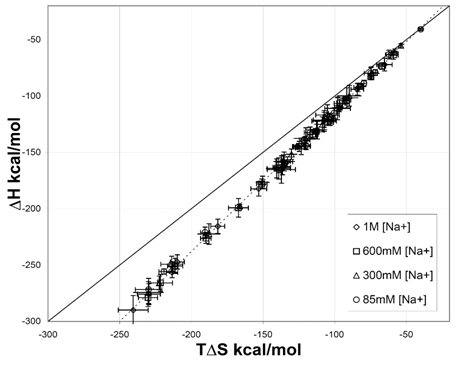
Figure 7 Correlation between $\Delta H_{cal}$  and $T\Delta S_{cal}$  (T = 298.15 K) for various short DNA duplexes in four different sodium [Na+] environments.⁴⁴

Release of [Na+] from the duplex upon melting can be quantified from the equilibrium shown in Equation 14. DNA melting is characterized by release and uptake of [Na+].⁵⁰ From the plot of $T_m^{-1}(K^{-1})$ versus $In\left[N{a}^{+}\right]$ , the release of ions that occurs upon melting, Δn can be evaluated according to the equation:

$\alpha \Delta n=\left(\frac{-\Delta H^0\left(d\left(T_m^{-1}\right)\right)}{R\left(dIn\left[N{a}^{+}\right]\right)}\right)$   (13)

where $\Delta H^0$ is the transition enthalpy of melting per nucleotide, R is the gas constant, expressed in [cal/(mol K)], Δn is the number of ions released per nucleotide, and σ = 0.90, is a correlation factor that accounts for the changes in the mean ionic activity coefficient of [Na+].^24,50

DSC-ligand interactions and the DSC

Because nucleic acids are common targets for many drugs, in order to optimize the efficacy of binding, as well as discover new therapies, it is important to fully characterize the thermodynamics nucleic acid-ligand interactions.^10,51 Efficient and rationale-targeted discovery of nucleic acid therapies involves full characterization of these interactions, including major/minor groove binding, intercalators, and other nucleic acid-ligand complex interactions¹⁰ DNA minor-groove binding molecules and dsDNA major-groove binding small organic molecules were discussed in detail elsewhere.³⁷

The determination of ligand to DNA binding parameters from two-dimensional DSC curves has been described in detail recently.⁵¹ Two basic methods of calculation of DNA-ligand binding parameters from melting data are: (1) the Ising Model,³⁰ and (2) the Chemical Equilibria Model¹² that is directly linked to statistical mechanics.^24,39,52 Generally, the chemical equilibria model is applicable to the DNA regions which melt by the two-state, simplex hybridization model, represented herein as:

$\left[2ssDNA\right]\rightleftharpoons \left[dsDNA\right]$   (14)

Where 2ss DNAs are complementary single strands, dsDNA represents the intact duplex (each species in their standard state), and $K^0$  is the standard state equilibrium constant for forming the duplex. Statistical thermodynamics describes the distribution and frequency of energy states of a system and partition function formalism can be useful in the analysis of calorimetric melting transitions.²⁴ In this approach, the populations of various molecular states of the system in equilibrium can be described by the chemical potentials and partition functions.⁵¹

The partition function is constructed considering multiple configurations that could be adopted by the two strands of the system.^24,25 In the simplex hybridization approach represented in Equation 14, the DNA molecules and associated solvent counter-ions are jointly considered as the solute, while the surrounding water molecules and unassociated ions are collectively treated as the solvent.²⁴ In addition, all solute species are assumed to be sufficiently dilute such that Henry's Law is applicable. The standard state equilibrium constant ($K^0$ ) for the simplex hybridization reaction in Equation 14 is given by:

$K^0=e^{-\Delta G^0/RT}$   (15)

The ratio of products to reactants is related to ΔGo by the following expression:

$\Delta G^0=-RT\ln K^0$   (16)

Where the standard state equilibrium constant,$K^0$ , reflects the relative probability of finding strands $2ssDNA$

andin their individual, standard states compared to finding them in the duplex state.²⁴ In multiplex hybridization reactions containing many probes and targets that must hybridize with high fidelity and specificity, reliable predictions of the melting stability of short DNA duplexes is crucial for performance and outcome. A detailed description of the reference state of DNA that uses the statistical thermodynamics formalism has been proposed, and published.^24,25,52

Some of the specific interactions between proteins and DNA that are fundamental to many biological processes have been reviewed elsewhere. These falls into three broad categories: (1) DNA sequence-dependent interactions, (2) DNA-protein interactions, and (3) DNA-based chemical modifications and interactions. Calorimetry of protein-DNA complexes and their components have also been revived elsewhere.²⁷

Effects of changing the pH, temperature, equilibria, and mixing ratio on the ligand-DNA interactions in solution provides additional information on the molecular level. The biophysical characterization of DNA on the formation and stability of a DNA-liposome complexes was investigated at different DNA/lipid molar ratios by⁵³ using an MC-2 Ultrasensitive DSC (MicroCal Inc.) and ITC.DSC revealed that DNAs ability to induce lipid mixing was probably related to its capacity to destabilize the lipid bilayer organization of the DNA/cationic liposome interactions. These results have utility in plasmid transfection properties and efficiency.⁵⁴

Used DSC to study the effect of DNA binding on specific anthracycline based antibiotics, ethidium bromide, and actinomycin D on stepwise melting of DNA. Stepwise DSC-DNA melting profiles were shifted in a characteristic manner, depending upon the interaction mode of the drug to the major or minor groove. The same group used DSC to measure the thermal stabilities of supercoiled and linear or open circular forms of plasmid DNA and various cellular transfections.⁵⁴ The stability of supercoiled DNA was attributed to changes produced in the tertiary structure of this form of DNA upon binding and is reflective of the importance of the topological constraint of DNA supercoiling.

The same research group also studied the effect of some intercalating drugs (the anthracycline type antibiotics, ethidium bromide, actinomycin D) on the stepwise melting of DNA. The DNA melting profiles of plasmids, bound by the intercalators, caused shifting of these peaks (thermograms) in a characteristic manner depending on the binding strength of the drugs.¹⁶ Carried out calorimetric studies of thermal denaturation of DNA and tRNAs. A MicroCal VP DSC (MicroCal, Inc.) was used to determine the$\Delta C_P^{ex}$  function of Tfor proflavine-DNA complexes.⁵⁵ Origin software was used to obtain the calorimetric thermodynamic profiles. The binding of small molecules like the acridine-based dye, proflavine, to DNA greatly stabilized the DNA helix. These studies are useful in developing better understanding of DNA targeted therapies. The nature of drug-DNA interactions and intercalating agents are presented in more detail elsewhere.^10,37 Determination of DNA-ligand binding parameters from two-dimensional DSC curves was reviewed elsewhere.⁵¹

Modified nucleic acids and calorimetry

Most molecular biology techniques in use today employ chemically synthesized nucleic acids and their derivatives.^11,26 Chemical modifications of nucleosides and nucleotides have several molecular biology applications.^5,21 Oligonucleotides (ONs) are laboratory-made, short, nucleic acid polymers that have a wide range of applications in genetic testing, microarrays, research, and forensics.^24,26 ONs bind, in a sequence-specific manner, to their respective W/C complementary ONs, and their chemically modified mimics²⁶ are routinely used in the laboratories to control the expression of fundamentally interesting or therapeutically relevant genes.¹¹ Locked nucleic acids (LNAs) are potent nucleic acid analogs used in therapeutics and biotechnology.²⁶

Locked nucleic acids are a class of nucleic acid analogs that contain a modified sugar structure, locked into a C-3’-endo and N-type polynucleotide conformation chain.⁵⁶ A LNA entity is a conformationally restricted nucleotide analogue exhibiting enhanced hybridization efficiency toward complementary strands. Therapeutic applications of LNA were reviewed elsewhere.⁵ Thermodynamics of DNA-RNA hetero-duplexes and effects of LNA nucleotides incorporated into various DNAs were investigated in detail.⁵ LNA has an extremely high affinity to complementary DNA and RNA and show improved mismatch discrimination relative to natural nucleic acids. Since the discovery of the HIV around 1983, a lot of progress has been made in the development of novel anti-viral drug.

Thermodynamic enthalpy-entropy compensations

Enthalpy-entropy compensation (EEC) is a characteristic feature of many biomolecular interactions.^3,38 Many calorimetric, thermodynamic measurements on processes involving biological molecules and ligand-biomolecular interactions exhibit EEC phenomenon. This ubiquitous phenomenon refers to the correlation that is sometimes observed between the large and opposing $\Delta H_{cal}$ and $\Delta S_{cal}$ values of reactions obtained from temperature-dependent data. With an increase in temperature, the $\Delta H_{cal}$ values became increasingly negative while the positive $\Delta S_{cal}$ values decrease. A detailed review on how to partition the individual thermodynamic contributions is done elsewhere.^38,45

EEC phenomena are important in biological molecule because $\Delta H_{cal}$ is almost compensated by a corresponding

$\Delta S_{cal}$ , resulting in a smaller net free energy change. This is the behavior proposed to result from biomolecular or ligand-biomolecular-water molecule reorganization, among other factors. A comparative study of calorimetrically derived thermodynamic profiles in drug-DNA binding studies was discussed by.³³ The nature of the thermodynamic forces,$\Delta H_{cal}$ and $\Delta S_{cal}$ that drive drug binding reactions and other biomolecular-ligand interactions must be examined carefully. These findings were also supported in calorimetry and thermodynamics in drug design.³ A more detailed picture regarding this phenomenon deserves a separate platform.

The broad focus of this review was to discuss the past and future use of DSC techniques in the study of fundamental components of the H-C transition in nucleic acids and their derivatives, with the primary aim of improving and optimizing this technology. DSC complements some computational techniques used in pharmacy and molecular medicine,¹⁵ in addition to other physicochemical methods. DSC data is collected as the $\Delta C_P^{ex}$ versus T.

Accurate evaluation of $\Delta C_P^{ex}$ is dependent on many factors such as buffer type, sample type, and pre- and post-transitional slope fitting.⁴⁴ DSC thermodynamic profiles for macromolecules requires the generation of a reproducible baseline buffer scan and this require the sample cell proper conditioning. Despite these challenges, DSC provides a direct evaluation of thermodynamic parameters, offers a number of advantages over optical absorbance methods and can be a cornerstone of modern molecular diagnostic approaches.

DSC is a sensitive, convenient, and powerful experimental tool for determining thermodynamic properties and mechanisms of biomolecules in elucidating drug-DNA interaction processes, and in providing data for improvement of existing drugs or for design of new drugs. The use of calorimetry in biophysics, drug design, and pharmaceuticals also provides information about the balance of driving forces (e.g. EEC), that cannot be obtained from structural or computational methods alone.

Mismatched bases (non-W/C) occur in the body and thermodynamically, ten mismatch configurations that involve the four bases have been identified and published.²⁹ The stability of these structures is of great interest due to their relevance in DNA repair, mutation studies, and Single Nucleotide Polymorphisms (SNPs). Higher order DNA complexes of nucleic acids like triplexes and quadruplexes have found potential use as a therapeutic agents.^4,11,36 DSC can provide information about thermodynamic profiles in these areas.

DSC has applications in probe-primer design technologies and is a highly sensitive thermal analysis technique that can be used to determine the stability of complex interactions and has utility in multiplex hybridization reactions. Another important piece of information that the DSC provides is the thermodynamic profiles of all potential configurations that form. These are developed and presented elsewhere.^24,25 In the process of designing probes for use in DNA diagnostic assays based on multiplex hybridization, it is essential to understand the thermodynamic stabilities of the designed probe, as well as target complexes that will form.

According to Wei et al.,⁵⁷ the human body is a complex biological system, and a single biomarker is not effective enough for accurate diagnosis.⁵⁷ Multiplexing assays of biomarkers at the point-of-care is an ever challenging goal for molecular diagnostics. Lack of sensitivity and specificity at early stages of diseases and progression may lead to over-diagnosis or under-diagnosis. As more molecular biomarkers are discovered for most diseases, the need for multiplexed, high-throughput detection techniques²⁵ are more important than ever. The use of DSC bio-sensing, based on nanoparticles has been reported.^23,57 This approach offers added advantages of simplicity of instrumentation, sharp melting peaks, indicative of high multiplicity, and large thermal scan ranges. These have a potential to make complex DSC bio-sensing capable of detecting simultaneous and multiple biomarkers.²³ However, this research is still at its infancy as far as being adopted by research and industrial communities. Further, the development of high-throughput and micro calorimeters that use less sample has been developed,⁴⁹ to conduct large amounts of chemical, genetic, and pharmacological tests efficiently.

The authors declare no financial, professional, personal or any other conflicting interests. No external funding was used in this study.

None.

None.

1. Bloomfield VA, Crothers DM, Tinoco IJ. Physical chemistry of nucleic acids. Harper and Row: New York, USA; 1974. pp. 294‒301.
2. Nelson DL, Lehninger AL, Cox MM. Lehninger principles of biochemistry. In: Freeman WH (Eds.), (5th edn), Molecular structure tutorials: Nucleotides; 2008.
3. Chaires JB. Calorimetry and thermodynamics in drug design. Annu Rev Biophys. 2008;37:135‒151.
4. Goodchild J. Therapeutic oligonucleotides. Methods Mol Biol. 2011;764:1‒15.
5. Kaur H, Babu BR, Maiti S. Perspectives on chemistry and therapeutic applications of locked nucleic acid (LNA). Chem Rev. 2007;107(11):4672‒4697.
6. Lando DY, Fridman AS, Chang CL, et al. Determination of melting temperature and temperature melting range for DNA with multi-peak differential melting curves. Anal Biochem. 2015;479:28‒36.
7. Patil SD, Rhodes DG, Burgess DJ. DNA-based therapeutics and DNA delivery systems: a comprehensive review. The AAPS J. 2005;7(1):E61‒E77.
8. Bhattacharya B, Mukherjee S. Cancer therapy using antibiotics. Journal of Cancer Therapy. 2015;6:849‒858.
9. Eriksson M, Nordén B. Drug-Nucleic Acid Interactions. Methods in Enzymology. 2001;340:68‒98.
10. Nakamoto K, Tsuboi M, Strahan GD. Drug-DNA interactions: Structures and spectra. Drug-DNA Interactions: Structures and Spectra. Methods Biochem Anal. 2008;51:1‒366.
11. Deleavey GF, Damha MJ. Designing chemically modified oligonucleotides for targeted gene silencing. Chem Biol. 2012;19(8):937‒954.
12. Bereznyak E, Gladkovskaya N, Dukhopelnykov E, et al. Thermal analysis of ligand-DNA interaction: determination of binding parameters. AIMS Biophysics. 2015;2(4):423‒440.
13. Chiu MH, Prenner EJ. Differential scanning calorimetry: An invaluable tool for a detailed thermodynamic characterization of macromolecules and their interactions. J Pharm Bioallied Sci. 2011;3(1):39‒59.
14. Bruylants G, Wouters J, Michaux C. Differential scanning calorimetry in life science: thermodynamics, stability, molecular recognition and application in drug design. Curr Med Chem. 2005;12(17):2011‒2020.
15. Fourches D. Application of Computational Techniques in Pharmacy and Medicine. Theoretical and Computational Chemistry. 2014;17:550.
16. Liu Y, Tan F. Calorimetric studies of thermal denaturation of DNA and tRNAs. Journal of Thermal Analysis. 1995;45(1):35‒38.
17. Sturtevant JM. Biochemical applications of differential scanning calorimetry. Ann Rev Phys Chem. 1987;38(1):463‒488.
18. Turner DH, Sugimoto N, Freier SM. RNA structure prediction. Annual Review of Biophysics and Biophysical Chemistry. 1988;17(1):167‒192.
19. Lewis EA, Murphy KP. Isothermal titration calorimetry. Methods in Molecular Biology. 2005;305:1‒16.
20. Bellini T, Cerbino R, Zanchetta G. DNA-based soft phases. Top Curr Chem. 2012;318:225‒279.
21. Gaglione M, Messere A. Recent progress in chemically modified siRNAs. Mini Rev Med Chem. 2010;10(7):578‒595.
22. Dagle JM, Andracki ME, DeVine RJ, et al. Physical properties of oligonucleotides containing phosphoramidate-modified internucleoside linkages. Nucleic Acids Res. 1991;19(8):1805‒1810.
23. Su M. Multiplexed detection of molecular biomarkers with phase-change nanoparticles. Nanomedicine. 2013;8(2):253‒263.
24. Manyanga F. Studies of DNA hybridization reactions and applications in genetic assays. Dissertations & Theses – Gradworks; 2009. pp. 168.
25. Horne MT. Theoretical investigations and microarray applications of DNA multiplex hybridization reactions. Dissertations & Theses – Gradworks; 2008. pp. 211.
26. Jepsen JS, Sørensen MD, Wengel J. Locked nucleic acid: A potent nucleic acid analog in therapeutics and biotechnology. Oligonucleotides. 2004;14:130‒146.
27. Read CM, Jelesarov I. Calorimetry of protein-DNA complexes and their components. Methods Mol Biol. 2001;148:511‒533.
28. Wartell RM, Benight AS. Thermal denaturation of DNA molecules: A comparison of theory with experiment. Physics Reports. 1985;126(2):67‒107.
29. SantaLucia J, Hicks D. The thermodynamics of DNA structural motifs. Annu Rev Biophys Biomol Struct. 2004;33:415‒440.
30. McGhee J. Theoretical calculations of the helix-coil transition of DNA in the presence of large, cooperatively binding ligands. Biopolymers. 1976;15(7):1345‒1375.
31. Poland DC, Scheraga HA. Theory of the Helix-Coil transition. Academic Press: New York, USA; 1970.
32. Bhindi R, Fahmy RG, Lowe HC, et al. Brothers in arms: DNA enzymes, short interfering RNA, and the emerging wave of small-molecule nucleic acid-based gene-silencing strategies. Am J Pathol. 2007;171(4):1079‒1088.
33. Breslauer KJ, Frank R, Blöcker H, et al. Predicting DNA duplex stability from the base sequence. Proc Natl Acad Sci USA. 1986;83(11):3746‒3750.
34. Dickerson RE, Drew HR, Conner BN, et al. The anatomy of A-, B-, and Z-DNA. Science. 1982;216(4545):475‒485.
35. Gomes AQ, Nolasco S, Soares H. Non-coding RNAs: multi-tasking molecules in the cell. Int J Mol Sci. 2013;14(8):16010‒16039.
36. De Clercq E. The design of drugs for HIV and HCV. Nat Rev Drug Discov. 2007;6(12):1001‒1018.
37. Paul A, Bhattacharya S. Chemistry and biology of DNA-binding small molecules. Current Science. 2012;102(2):212‒231.
38. Searle MS, Williams DH. On the stability of nucleic acid structures in solution: enthalpy-entropy compensations, internal rotations and reversibility. Nucleic Acids Res. 1993;21(9):2051‒2056.
39. Crothers DM, Zimm BH. Theory of the melting transition of synthetic polynucleotides: evaluation of the stacking free energy. J Mol Biol. 1964;9(1):1‒9.
40. Zimm BH, Bragg JK. Theory of the phase transition between Helix and random coil in polypeptide chains. J Chem Phys. 1959;31:526.
41. Wartell RM, Benight AS. Thermal denaturation of DNA molecules: A comparison of theory with experiment. Physics Reports. 1985;126(2):67‒107.
42. Jelesarov I, Bosshard HR. Isothermal titration calorimetry and differential scanning calorimetry as complementary tools to investigate the energetics of biomolecular recognition. J Mol Recognit. 1999;12(1):3‒18.
43. Brown A. Analysis of cooperativity by isothermal titration calorimetry. Int J Mol Sci. 2009;10(8):3457‒3477.
44. Gill P, Moghadam TT, Ranjbar B. Differential scanning calorimetry techniques: applications in biology and nanoscience. J Biomol Tech. 2010;21(4):167‒193.
45. Breslauer KJ, Freire E, Straume M. Calorimetry: A tool for DNA and ligand-DNA studies. Methods Enzymol. 1992;211:533‒567.
46. Dickman R. Thermodynamic effects of 5’and 3' single strand dangling ends on short duplex DNA. Dissertations and Theses; 2010. p. 94.
47. Freyer MW, Lewis EA. Isothermal titration calorimetry: Experimental design, data analysis, and probing acromolecule/ligand binding and kinetic interactions. Methods Cell Biol. 2008;84:79‒113.
48. Black J, Robinson J, Chemist P, et al. Lectures on the Elements of Chemistry. Mundell and Son for Longman and Rees, Edinburgh, London, England; 1803.
49. Zhuravlev E, Schick C. Fast scanning power compensated differential scanning nano-calorimeter: 1. The device. Thermochimica Acta. 2010;505(1-2):1‒13.
50. Owczarzy R, You Y, Moreira BG, et al. Effects of sodium ions on DNA Duplex Oligomers: Improved predictions of melting temperatures. Biochemistry. 2004;43(12):3537‒3554.
51. Dukhopelnikov EV, Bereznyak EG, Khrebtova AS, et al. Determination of ligand to DNA binding parameters from two-dimensional DSC curves. J Therm Anal Calori. 2013;111(3):1817‒1827.
52. Gilson MK, Given JA, Bush BL, et al. The statistical-thermodynamic basis for computation of binding affinities: A critical review. Biophys J. 1997;72(3):1047‒1069.
53. Pector V, Backmann J, Maes D, et al. Biophysical and structural properties of DNA•diC14-amidine complexes. Influence of the DNA/lipid ratio. J Biol Chem. 2000;275(38):29533‒29538.
54. Maeda Y, Nunomura K, Ohtsubo E. Differential scanning calorimetric study of the effect of intercalators and other kinds of DNA-binding drugs on the stepwise melting of plasmid DNA. J Mol Biol. 1990;215(2):321‒329.
55. Basu A, Kumar SG. Thermodynamic characterization of proflavine-DNA binding through microcalorimetric studies. The Journal of Chemical Thermodynamics. 2015;87:1‒7.
56. Maderia M, Shenoy S, Van QN, et al. Biophysical studies of DNA modified with conformationally constrained nucleotides: Comparison of 2′-exo (north) and 3′-exo (south) ‘locked’ templates. Nucleic Acids res. 2007;35(6):1978‒1991.
57. Wei F, Patel P, Liao W, et al. Electrochemical sensor for multiplex biomarkers detection. Clin Cancer Res. 2009;15(13):4446‒4452.