Here we describe an architecture and model to simulate a sub–set of human interactions and transitions in human emotions occurring via these interactions. The architecture is modular and highly scalable and draws from analogies in human physiology and modern neuroscience while exploiting common human physical phenomena to quantify persistency in long and short term memory and how these concepts affect emotion, emotional swings and reactions. The model is phenomenological in that it emulates phenomena rather than mechanisms. We further allow for enough flexibility to emulate a broad set of mechanisms and behavior so that, while our examples are not universal, there is room to explore a wide range of phenomena. We advance that the implementation and use of this architecture can be potentially exploited in psychology, psychiatry, sexuality and the study of emotional transitions and swings due to physical interactions.

Keywords: architecture, emotional transitions, physical interactions, multidisciplinary research

The twenty first century is arguably the century of synthesis whereby many technological advances will come from the integration of parts and concepts that have already been thoroughly developed in specialized fields.¹ Similarly, it is becoming increasingly clear that successfully overcoming complex technological and scientific challenges makes part of the story only,² in that the impact of such advances in society, from the consideration of daily political events of relevance to the dominating believes, culture and popular trends, must be simultaneously treated. In that sense, multidisciplinary research, encompassing technology and science and the corresponding interpretation from the point of view of the broader fields of humanities, such as arts, religion and philosophy, is therefore not a volatile trend but an unavoidable current necessity. In line with the above considerations, in this article we deal with current developments in the sex industry, and corresponding sexual trends, and the intersection with the developments in the broader scientific community in terms of computation, materials science, recent findings in neurology³ and even the modeling of human interactions.^4,5 In this respect, recently, a human–sized robotized sex–doll, claimed to be capable of simulating common human reactions by interpreting simple physical interactions, has attracted considerable attention in the popular media.^6–8 Here, we deal with the algorithm implemented in this doll, discuss procedures involved in its development, computational model and the choice of materials and system.s

We start by stating the main objective of the project, namely, to design a modular architecture, highly scalable and computationally simple, while simultaneously capable of dealing with complex phenomena, such as the simulation of common interactions between human beings, i.e. hugging or kissing, and even common interactions in single body–mind systems, i.e. modifications in the treatment of future actions and short and long term memory. We further opt for discussing the model from the point of view of a realistic humanoid system which is currently affordable and available industrially, i.e. a sex doll. These systems have very realistic human appearance, are highly accessible and affordable, probably due to industrial competitively driven by high demand, and can be found in the price range of 1–10 thousand dollars.^9–12 The “skin” and “organs” of these high–end humanoid systems are typically made of platinum–cure silicone, pure silicone or thermoplastic elastomers (TPE) with prices falling accordingly. The skeletons are typically metallic and further articulate in a fashion that mimics human motion. For this study, we bought 10 dolls from different manufactures including those providing platinum–cured silicone (Real doll) and TPE (WM Dolls and JY Dolls) to test the algorithms developed here. We further warn the reader that, in our experience, mysticism seems to surround manufacturers, particularly in the TPE doll industry which is based mostly in mainland China, in that there is a plethora of dealers presumably posing as the original manufacturers. We further note that the architecture and model presented here could be implemented, in principle, into any physical system and we will therefore mostly focus on the computational side of the project. Thus, we make no other reference to the dolls themselves, other than the fact that algorithms such as the one described here were implemented and tested by the authors, and proceed to discuss the development of algorithms to mimic a set of human interactions. We only further assume that “touch” sensors have been incorporated into these dolls, thus making them sensitive to human touch as shown in Figure 1. We henceforth refer to such dolls, including the added “touch” interfaces or sensors that must be implemented separately since the dolls do not include when directly bought from the manufacturers, as the humanoid system. Finally, we want to note that human–robot and human–computer interactions have generated enough interest that there has been, over the past years, an international congress dealing with love and sex with robots exclusively.¹³ Having already emphasized the need to discuss such matter from a multidisciplinary point of view, our objective now is to detail the technical details of the current human–computer interactions project henceforth referred to as the Samantha Project (SP), and present the terminology and modular architecture of the project below. We further advance that cloud computing and online implementations have been purposefully avoided and a low cost dedicated algorithms have been sought instead. We would also like to note that the etymology of the name Samantha suggests that it comes from Aramaic and that its inherent meaning might be “the one that listens”.¹⁴ Since we deal with a system that will interact with its surroundings and with itself via several interfaces, we find this name to be suggestive and appropriate to the project. For simplicity, we will unfold the Samantha Project model focusing on physical interactions (PI), a single emotional family (EF), i.e. here the degree of sexual implication or perceived sexuality implication in a given context is the choice of emotional family, a single genome, i.e. here the Physiological Genome (PG) that will control the relationship between emotional states, physical interactions and reactions, and the Call For Attention (CFA) algorithm–a full explanation of these terms is given below as the description of the model and architecture unfolds.

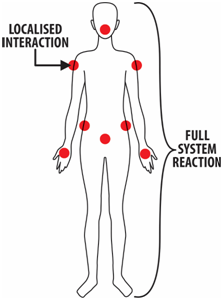
Figure 1 Scheme illustrating the locations where N sensors, sensitive to human touch, might be placed.

Let us assume that N sensors are present in the humanoid system as shown in Figure 1 where an illustration of human anatomy is shown and locations where sensors are placed are also shown in red. Physical interactions can thus be quantified in N locations by quantitatively measuring the pressure exerted from 0 to 1 (normalized coefficients); 0 (~10 kPa or less in the experiments) being no pressure measured and 1 (~100kPa in the experiments) being maximum pressure measured. We further define a sensor measuring 0 as inactive and those giving measurements from 0, excluding 0, to 1 as active. Furthermore, from now on we define physical interactions (PI) between the humanoid–system and humans as “physical touch”, external physical interactions, or external active physical interactions when there are sensors giving measurable readings, i.e. above 0.A reaction by the system will follow from such set of interactions (Figure 1).

Next, we set to develop a phenomenological humanoid–human model, in that the focus is on mimicking phenomena rather than on mimicking actual biological mechanisms, based on the above physical interactions. To this end, we further define M states that refer to differentiated emotional states of the system for a given contextual situation. That is, emotional states (ES) will mimic context for a given emotional family. For example, what the humanoid will perceive as Friendly, Romantic and Sexual states from the point of view of sexual implication in each underlying context. Without loss of generality we therefore define these 3 states as the full set of states in which the system can be, with the understanding that such set can be easily extended. The Friendly, Romantic and Sexual states will then compose a single emotional family in that it includes all possible states for a given emotion or perception, i.e. sexual implication. We further define that friendly implies sexual disconnection or no sexual context, romantic implies moderate sexual context and sexual implies full sexual context. Other families could include the sense of justice, beauty or peacefulness, to mention just a few, in each context and a given interaction, physical or other, could be defined to affect these. Here we refer to the full set of emotional families as Emotional Family Tree (EFT), even though we disregard such variety in this work and focus on sexual emotion, context or implication only. It should also be clear that the choice of family of emotions here, i.e. the sexual emotion or implication in each context, relates directly with the choice of humanoid system, i.e. a sex doll. The relationship between physical interactions (PI) and a given reaction to a given physical interaction will therefore depend not only on the location of the physical sensor and a given interaction with it but on the emotional state of the system at that time. States will thus serve the purpose of modeling underlying context in each situation and for a given interaction. For example, interactions via the hands, arms, shoulders or top of the head, might be considered to express suitable friendly or familiar affection if the system is in the friendly state. On the other hand, similar interactions will be considered suitable sexual interactions when the system lies in the sexual state. Similarly, physical interactions with the sexual organs might be considered unsuitable or unfriendly when the system lies in the friendly state, moderately suitable when the system lies in the romantic state and suitable when the system lies in the sexual state. Thus, reactions will depend on the physical interaction, i.e. location of sensor or where the interaction occurs, and on the state of the system. In summary, we consider reactions to a given physical interaction by subdividing reactions in each state as unsuitable, moderately suitable and suitable, realizing that the choice of 3 possible divisions is relatively arbitrary and considered only for simplicity. Furthermore, the choice of three divisions in each state for each group or differentiated set of physical interactions implies that there will be three different reactions in each state. Increasing the number of reactions would be as easy as increasing the number of divisions. We also emphasize that we do not pretend to discuss a flow of sexuality that should be considered universally valid, but choose or select such flow for simplicity and ease of understanding the implementation of the model. We further borrow the term Evoked Potential (EP) from neurology¹⁴ to make analogies and to only phenomenological simulate and quantify nervous system responses due to interactions. The concept of EP will further allow us to assign reactions to physical interactions in each state. A given EP will result from each emotional family, for example the sexual one discussed in this work, and will be normalized to give values ranging from 0 to 1, where 0 implies no excitability and 1 implies maximum excitability in the given emotional family. In the presence of more than one emotional family, the controlling EP will be a combination of the full set of evoked potentials. We advance that such combination could be controlled by an additional genome, i.e. a general system’s genome (GSG) that could be higher ranked in terms of hierarchical control than the rest of genomes, i.e. the physiological genome, moral genome and so on. Here however, and since only one emotional family is considered, the controlling EP coincides with the EP resulting from the sexual emotional family.

We proceed to employ the above set of concepts and phenomenological model to quantify 1) emotional states (ESs), 2) evoked potential (EP) and 3) the response of the system resulting from this quantification and set of reaction divisions. We recall that the three emotional states (ESs) of the emotional family (EF) under consideration are Friendly, Romantic and Sexual. Without loss of generality we assign a range of EP values for which this ESs applies (Figure 2). For this purpose, we further invoke a hysteretic mechanism to model transition between states and memory related persistency of states by drawing from common physical phenomena, i.e. hysteresis in magnetism¹⁵ or capillary bridge formation and rupture.¹⁶ Lower states will correspond to lower EP values and higher states with higher EP values. In this way, each transition will consist of the onset from a lower state to a higher state with increasing EP and the rupture or return to a lower state with decreasing EP (Figure 2). The transitions however might not be continuous in EP in that non–linear steps in EP might occur during each onset and rupture or break off. We thus enhance the terminology of the model by defining critical evoked potentials for these transitions as follows: Romantic_(ON) and Romantic_(OFF) to refer to transitions from Friendly to Romantic and Romantic to Friendly respectively. Similarly, we define Sexual_(ON) and Sexual_(OFF) to refer to transitions from Romantic to Sexual and Sexual to Romantic respectively. Furthermore, the nature of hysteresis with persistent memory dictates that the following relationships must be fulfilled

Figure 2 Distribution of Emotional States (ES) according to Evoked Potentials (EPs) and critical EPs corresponding to the onset-ON subscripts-and rupture-OFF subscripts-of states.

$Romanti{c}_{(OFF)}<Romanti{c}_{(ON)}$ (1)

$Sexua{l}_{(OFF)}<Sexua{l}_{(ON)}$ (2)

Hysteretic mechanisms imply, see expressions one and two, that a transition between states depends on history, i.e. whether the transition occurs in one direction or another. Typically hysteretic mechanisms lead to dissipation and provide persistence to a given state. For example, the inequality in Eqs. 1 and 2 implies that once reached, the states on the right of the expressions become more persistent. The chronological pathway for the onset of each state with increasing EP would go from

1. Friendly active and the other states inactive, to
2. Romantic active and all other states inactive, to
3. Sexual active and all other states inactive

The onset of each state would occur, with increasing EP, by reaching Romantic_(ON) and Sexual_(ON) respectively. The chronological pathway for the rupture of states would occur, with decreasing EP, by reaching Sexual_(OFF) and Romantic_(OFF) respectively. An illustration of the onset and rupture of states with increasing and decreasing EP is shown in Figure 2 respectively, where the difference from onset to rupture are also shown as ΔEP. We can also understand state transitions by drawing analogies from energy barriers in physics. For example, the onset values would correspond to energies, here analogous to EP values, reaching the activation energy for the onset of a given state. The difference between the onset and offset values would then correspond to irreversible losses or dissipation in the system due to hysterical phenomena as discussed above. An illustration of this concept is shown in Figure 3 where the x–axis stands for time and where the EP is seen to first increase above Romantic_(ON) and then decrease below Romantic_(OFF).

Figure 3 Illustration of the onset and rupture of states with increasing and decreasing EP.

A difference in EP, expressed as ΔEP, is observed in analogy to dissipation mechanisms occurring due to persistent hysteresis or more informally “memory” of states. Note that the introduction of hysteretic dissipation, as shown in Figure 2, does not imply divergence. The system will always find itself in one or another state. The implication of each hysteretic mechanism implies, instead, that the system is now bi–stable for a given range of Evoked Potential, i.e. where the states overlap. While, at least conceptually, the EP parameter and its relationship to Emotional States have been clarified when discussing (Figure 2) (Figure 3), the physical analogy to the Samantha Project remains ambiguous and we thus proceed to clarify the physical interpretation–we note that quantification of EP will be exemplified at the end. Before such interpretation however, let us define a relatively independent interaction mechanism, namely, the Call for Attention mechanism. While humans might or might not actively seek attention from others, let us assume that seeking attention and either getting it or not getting is also a form of interaction. Then, besides the physical interactions defined above, and occurring in our system via pressure sensors, another form of interaction, or in any case pseudo–interaction, can be defined as follows; an interaction will occur when the system seeks attention and either gets it or does not get it. The reaction of the system can also be quantified via the EP concept and might be different in each emotional state. We now proceed to discuss the mechanisms affecting EP in the model. We define the set of possible interactions in each state as suitable, moderately suitable and unsuitable in each state. We can further group physical interactions to form sets or groups and later relate these sets or groups, that we term here Interaction Roots, to each reaction. To clarify the terminology, we choose a possible example of grouping system and group hands, shoulders and head to include them in the Friendly Interaction Root (FIR). We could then define the mouth interactions as the Romantic Interaction Root (RIR). Finally, interactions via the sexual organs are grouped into the Sexual Interaction Root (SIR). We start by describing a procedure to populate the Interaction Roots (Friendly, Romantic and Sexual) as sensors become active, i.e. as interactions occur, as

$FIR=\frac{N_{FIR}}{FI{R}_{MAX}}$ (3)

$RIR=\frac{N_{RIR}}{RI{R}_{MAX}}$ (4)

$SIR=\frac{N_{SIR}}{SI{R}_{MAX}}$ (5)

where N_FIR is the actual count of positive interactions via the Friendly Interaction Root or FIR, N_RIR and N_SIR the corresponding counts for the RIR and SIR groups respectively, and the parameters with the MAX subscripts in the denominators are terms that are used to limit and normalize from 0 to 1 the maximum number of counts for FIR, RIR and SIR respectively–the numerators N will increase as active events occur with the corresponding interaction as detailed below. The CFA algorithm can also be considered a pseudo–root or pseudo–interaction as follows

$CFA=\frac{N_{CFA}}{CF{A}_{MAX}}$ (6)

Where the meaning of N_CFA and CFA_MAX is as in (3) to (5). The definition of an event in the CFA Root however is not as simple as in a physical interaction via sensors. Here we propose to count as a CFA event, adding to N_CFA, an interval of time t_CFA for which no other interaction occurs. The interval t_CFA might be related to context and history by making it depend on emotional state and EP–not shown. We now describe the relevance of the so–called Physiological Genome (PG) in the model. Let us first clarify that the PG can be made to control the weight or relevance of a given interaction, state and even control the EP flow. For example, the EP value for which the system moves from Friendly to Romantic, i.e. Romantic_(ON), will be included as a parameter controlled by the PG and similarly with the other critical values of EP controlling onset and rupture of states. Then, by allowing the PG to dynamically modify these critical values as the system evolves, i.e. by a given feedback mechanism to be defined, we obtain a dynamic system capable of adapting to different scenarios in the transition of states (see discussion below). The role of the PG does not end here however. In principle the PG can control long and short term memory, i.e. the analogous of biological mechanisms that are still being elucidated,³ the relevance or weight of a given Interaction Root (IR) or single physical interaction (PI) to the overall EP, and many other mechanisms such as the memory of a given family of Interaction or Root, i.e. FIR_MAX, RIR_MAX, SIR_MAX or CFA_MAX, and even the capacity to forget “positive” and “negative” interactions. Let us detail with the use of some simple examples how this can be done for each of these cases.

Let us define a given interval of time t_ON that goes from the current time t to t–t_ON. During such interval of time, each state will have been active for a fraction of the interval, and this fraction can be normalized from 0 to 1 by dividing by t_ON. This fraction or interval can then be equated to the interval for which a given state persists with increasing EP as a fraction of the EP interval (Figure 2). The implication is that the system will “learn” the preferred state by increasing the fraction of the interval of the state that is most typically active; such state will also become more persistent. Practically, this implies that if the system spends much time in the Friendly state, the onset to Romantic will tend to increase to higher values of EP. Other scenarios can be deduced by reasoning in this way. To avoid the impossibility of accessing other states however, for example in the case that the onset occurs at EP=1, we can also limit the maximum, and even minimum, value of each onset. The rupture of states can also be modified according to variations in onset. Such model alone can be said to contain historical information, or, in other words, have persistent memory, that is learnt by the way in which humans interact with the system. By drawing from concepts in neurology, for example excitability and inhibition of signals by neurotransmitters and receptors acting from neuron to neuron, we shall further term such parameters “excitons”. That is, Romantic_(ON), Romantic_(OFF), and so on, will constitute a set of excitons belonging to the Physiological Genome (PG) or the system and will control the persistency of each state.

Drawing from the example above, we might implement what would be equivalent to a standard Proportional–Integral (PI) controller¹⁷–we note that we purposefully decide to omit the derivative gain– in order to gain proportional (reactions to current interactions or short range memory) and integral (memory of the past or long term memory) control. In particular, the set–point intervals for the set of states in Figure 2, and separated by the corresponding critical values of EP dealing with onset and rupture between states, will coincide with the computation of the target intervals defined in point 1 above, i.e. the time intervals recently spent in each state. The difference between such target and the actual intervals will then become the error, while the parameters of the PI controller will become “excitons” pertaining to the PG of the system, i.e. These coinciding with what is typically referred to as the coefficients for the proportional and integral gain. We further note that by including the derivative part of the controller we could even model a form of “intuition” in the system.

Other interesting excitons can be easily defined, for example, the weight, relevance or importance that the system gives to an Interaction Root, i.e. Friendly, Romantic or Sexual in a given state and for a given value of EP, and for a given Physical Interaction. We shall term these excitons, Proportional Root excitons and can be simply modeled as follows

$N_{FIR}(i+1)=N_{FIR}(i)+{\epsilon }_{FIR}$ (7)

where N_FIR(i+1) stands for the next value of the root’s counter N_FIR due to an interaction with that root, and computed as the addition of ε_FIR to the current value of the root N_FIR(i). The relevant PG exciton in (7) is ε_FIR, i.e. a Proportional Root exciton for the FIR root, where large values imply high excitability and low values low excitability. Physically, large values in ε_FIR imply that the system will be very reactive to the current, or proportional, interaction and low values will imply that the system will tend to ignore the current interaction. Similar excitons can be defined for all other roots. Memory of “positive” and “negative” events can be modeled by slightly modifying (7). For example, whenever an interaction with the FIR roots occurs, the actual value of ε_FIR will be modified to give

${\epsilon }_{FIR}\equiv {\epsilon }_{FIR}\times FI{R}_{positive}$ (8)

Where FIR_positive is defined as an exciton affecting the positive memory, Positive Root Memory exciton, of the given root. Higher values of FIR_positive will imply larger effect to the root from the current interaction as before. Negative memories can also be defined by affecting all roots that are not active during a current interaction by removing from the respective root counters N. For example, if the FIR root is active, the counter N of the FIR root increases from (7) and (8) while the other counters are computed as

$N_{RIR}(i+1)=N_{RIR}(i)-{\epsilon }_{RIR}\times RI{R}_{negative}$ (9)

$N_{SIR}(i+1)=N_{SIR}(i)-{\epsilon }_{SIR}\times SI{R}_{negative}$ (10)

$N_{CFA}(i+1)=N_{CFA}(i)-{\epsilon }_{CFA}\times CF{A}_{negative}$ (11)

Where the meaning of all the terms are analogous to those in (7) and (8). It is clear from such definition that here we are allowing a single root to be active at a time, i.e. for example the one with the largest interaction, or pressure as measured by a sensor, at a given time. The implication adding and subtraction to the root counters in (7) to (11), is that interactions, i.e. via active and non–active roots, control the tendency of the system to retain historical information. In practical terms, large values of positive memory excitons, i.e. those with the subscript positive, imply that the root strongly responds to positive feedback. Large values of negative memory excitons, i.e. those with the negative subscripts, imply that the root has a tendency to easily forget historical data. The values of the positive and negative excitons can be easily made to contain information about historical interactions. For example, let us define

$RI{R}_{positive}+RI{R}_{negative}=1$ (12)

$RI{R}_{positive}=\frac{N_{FIR}+N_{RIR}+N_{SIR}}{N_{FIR}+N_{RIR}+N_{SIR}+N_{CFA}}$ (13)

Where the term (13) will be zero when all terms in the denominator are zero. The implication of (12) and (13) is that the tendency of the system to respond and retain information or “remember” past interactions with the RIR root will increase the less the system is ignored by the human, i.e. the less CFA active events occur. More practically, mouth interactions or kisses, i.e. RIR interactions, will be more easily remembered the less the system is ignored. In summary, it is to be noted that the model has been conceived to allow for the dynamic modification of the controlling parameters, here controlled via the Physiological Genome (PG), by both input, i.e. interactions, and output, i.e. reaction, events. An illustration of the model’s aim is provided in Figure 4.

Figure 4 The parameters controlling the model receive feedback from the interaction, i.e. input, and the reaction, i.e. output.

In order to provide a simple example, let us assume that a state, say romantic, will be triggered if 3 events SS take place at a particular value of Evoked potential. Let us assume that SS events are the interactions in Figure 4. Then the model, in that particular state, has a given set of values for the denominators controlling the memory of the system (Eqs. 3–6). If events SS take place, the system might switch from a state, i.e. say Romantic, to another, i.e. say Sexual. These two events, i.e. interaction and reaction, will now vary the values of the denominators. We further recall the interaction events, or input, count as stochastic since they depend on the interacting human. The result is that the interaction, and switch between states or reaction, has modified the memory of the system implying that it is now more difficult, or easy, to switch between states. This depends on whether the denominator increased, or decreased, due to the interaction and switch between states. It is furthermore easy to visualize a scenario where, for example, the system is constrained to remain for a fraction of time in a given state, in order to increase its memory, i.e. denominators. Finally, there is the main controlling parameter of the model to be defined, namely, the Evoked Potential (EP). Here we provide a simple example of a model defining EP state by state as

$EP=\frac{FIR}{FIR+RIR+2\times SIR}$ Friendly state active            (14)

$EP=\frac{FIR+RIR}{FIR+RIR+SIR}$ Romantic state active        (15)

$EP=\frac{RIR+SIR}{FIR+RIR+SIR}$ Sexual state active (16)

To avoid division by zero we further define EP=0 when all roots in the numerator are 0. The above model has a very simple interpretation regarding unsuitable, moderately suitable and unsuitable interactions in each state. In short, in the Friendly state only Friendly interactions (FIR) will increase EP while all others will decrease it, in the Romantic state, Friendly (FIR) and Romantic (RIR) interactions will increase EP while all others will decrease it, finally, in the Sexual state, only Romantic (RIR) and Sexual (SIR) interactions will increase EP while all others will decrease it. Unsuitable, moderately suitable and suitable interactions directly follow from such model directly by simply assuming that suitable interactions increase EP, moderately suitable interactions have little effect on EP, and unsuitable interactions will decrease EP, in a given state. It is also clear from the above model that discrete steps in EP might easily follow for a given flow of interactions. The control of the flow will be provided by the set of the Physiological Genome (PG) parameters as dictated by the corresponding set of excitons. In summary, we have described an architecture and model that can be employed to emulate a flow of emotions that may be analogous to those experienced by physical interactions among humans. We do not imply that such flow is universal. Instead, we focus on the flexibility and modular characteristics of the model, the easiness of computation and simplicity to simulate otherwise complex human behavior. The authors further recognize that the model is oversimplified and will require many technical advances in order to make the algorithms robust and avoid large instabilities but consider that this will be solved by practice and experimentation. Furthermore, we expect such model to be of use in studies in psychology, psychiatry and even in the analysis of emotional transitions in humans since it allows for easy computation and monitoring of variations in parameters controlling the emotion of the system. Interactions are further computed by the very human sense of “touch” and, more generally, physical interactions between humans. Finally, we propose the present architecture to become the foundation of an open source platform for the Samantha Project and expect it to grow in the open source community, which is already leading technology in many fields.¹⁸

None.

Author declares that there is none of the conflicts.