A Rubik’s Snake is an interesting toy which can be thought as a serial chain with applications in the construction of reconfigurable modular robots. In this paper, we present some theorems related to a Rubik’s snake with palindromic, periodic and Möbius properties. Examples are given for shape design using such properties.

Keywords: Rubik’s snake, Möbius strip

The Rubik’s Snake is an interesting toy invented by Prof. Erno Rubik in 1981.¹ Since then, it has been used as a tool for the study of protein folding^2,3 and for the construction of reconfigurable modular robots.^4–6 It can be viewed as a serial chain.⁷ More applications of robots can be found in.^8,9 Also, some ideas in the study of Rubik’s Snake are also used in rigid Origami folding.^10,11 Strategies have been given for the design of a Rubik’s Snake in¹² and rotations that are not integer multiple of 90 degrees are also mentioned. Some mathematical problems concerning a Rubik’s Snake have been studied in¹³ with several theorems proved. In this paper, we study Rubik’s Snake sequences with palindromic, periodic and Möbius properties. We will first present some theorems in Section 2 and then present some examples for shape design in Section 3. We conclude in Section 4.

We first present some path independence theorems. Some of the results are useful later when proving theorems about palindromic snake and Möbius snake. A rotation degree sequence is the degree sequence defined in:¹³ 0 means the snake is like a ruler going straight. 2 means a joint is rotated by 180 degree. -1 and 1 means a joint is rotated to the left or right by 90 degrees. The direction of a block is also defined in.¹³ A block of Rubik’s Snake can have two possible directions. When the entrance and exit square faces are interchanged, the direction is changed.

Theorem 1

We call the first block of the snake “start” and the last block of the snake “end”. If the start and end blocks are fixed and their directions are fixed, then the parity of the sum of degrees of this snake is also fixed. (i.e., the parity of sum of degrees is path independent)

Proof: We use the idea of a “U-turn path” as follows. By following the sequence [0 1 -1 2 0 -1 2 0], a snake can trace back to overlap the first piece again except that the direction is changed, i.e., the entrance be- comes the exit. Figure 1 shows the geometry of this U-turn path. Note that the entrance of the first block is the exit of the 9th block. Suppose there are two snake paths connecting the starting block and the end block. We could first trace along the first path, then trace along a U-turn path, then trace along the second path backward, then another identical U-turn path. This forms a closed loop, though crashing occurs. It is proved in¹³ that the closed loops have an even number as the sum of degrees. Clearly, two identical U-turn paths contribute to an even number of the sum of degrees. Also, going forward and backward do not make a difference in the degrees. Therefore, the two paths have the same parity of the sum of degrees.

Figure 1 A U-turn path.

Theorem 2

If the start and end blocks are fixed, then the parity of the number of blocks of the snake is also fixed. (i.e., independent of path or directions of the start and end blocks)

Proof: We use the same idea of U-turn path. Suppose there are two paths connecting the starting and end- ing blocks. The first path, plus a U-turn path or not (depending on the directions), plus the second path in reverse direction, plus another U-turn path or not (depending on the directions), form a closed loop. It is shown in¹³ that the total number of blocks is even. If no U-turn path is added, the sum of number of blocks of two paths is the number of blocks of a closed loop plus 2, which is even. If only one U-turn path is added, then 9 U-turn path blocks are added but the closed loop would be missing one block from one of the two paths (start or end). The sum of number of blocks of two paths is the number of blocks of a closed loop minus 9 then plus 1, which is even. If two U-turn paths are added, then 18 blocks in U-turn paths are added. The sum of number of blocks of two paths is the number of blocks of a closed loop minus 18, which is even. In all cases the two paths must have the same parity for the number of blocks.

One interesting topic for Rubik’s Snake is to require the degree sequence to have the palindromic property. A snake with such property is symmetric with respect to a line.

Definition 3 A non-closed loop snake sequence is palindromic if it remains the same when reading backward. In other words, it is either of the form $\left[a_1,\mathrm{....}{a}_n,a_n,\mathrm{...}{a}_1\right]$ which we call type I, or $\left[a_1,\mathrm{....}{a}_{n-1},a_n,a_{n-1},\mathrm{...}{a}_1\right]$ which we call type II. A closed loop (including the rotation from the last block to the first) is palindromic if there exist at least one rotation of the sequence of the form $\left[a_1,\mathrm{...}{a}_n,a_n,\mathrm{...}{a}_1\right]$ which we call type I, or $\left[a_1,\mathrm{...}{a}_{n-1},a_n,a_{n-1},\mathrm{...}{a}_2\right]$ which we call type II.

Note that there are also $\left[a_1,\mathrm{...}{a}_n,a_n,\mathrm{...}{a}_2\right]$  or $\left[a_1,\mathrm{...}{a}_{n-1},a_n,a_{n-1},\mathrm{....}{a}_1\right]$ palindromic closed loops for general rotation angles. However, for integer multiple of 90 degree rotation, it is proved in¹³ that the number of blocks is even for closed loops and these two have odd number of blocks, which cannot happen.

Theorem 4

There exists at least one axis such that when a Rubik’s Snake with palindromic sequence rotates around the axis by 180 degree, the resulting shape coincides with the original shape.

Proof Firstly, we will discuss about the non-closed loop. 

Case 1 For the sequence $\left[a_1,\mathrm{.....}{a}_{n-1},a_n,a_{n-1},\mathrm{.....}{a}_1\right]$ , we will discuss all the cases based on what $a_n$ is. We have the following cases.

Case 1.1 $a_n=0$ As we show in Figure 2, this square refers to the square face in the snake with degree $a_n$ , the circle of dashed line means going inside the paper for two more vertices and circle of solid lines means going outside the paper for two more vertices.

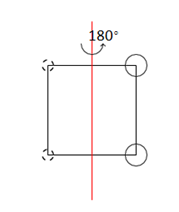
Figure 2 $a_n=0$ .

Case 1.2 $a_n=1$ or -1

We show this case in Figure 3.

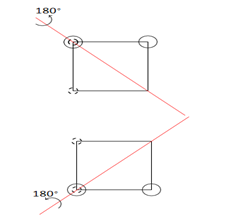
Figure 3 $a_n=1$ or $-1$ .

Case 1.3 $a_n=2$

We show this case in Figure 4.

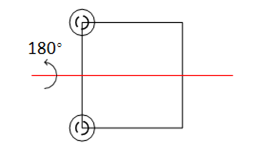
Figure 4 $a_n=2$ .

Case 1.4 $-1<a_n<1$

We show this case in Figure 5.

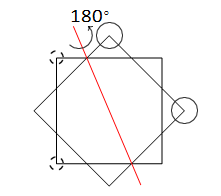
Figure 5 $-1<a_n<1$ .

Case 1.5 1 $1<a_n<2$ or $-2<a_n<-1$

We show this case in Figure 6.

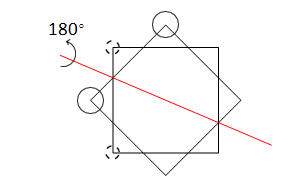
Figure 6 $1<a_n<2$ or $-2<a_n<-1$ .

We can see in all cases above, since the two blocks with a_n rotation in between will coincide when one of them rotates about the axis in the figure by 180- degree, and the sequence around a_n are identical if reading from a_n to other sides, so the overall shape of the snake must be coincide with itself if rotate 180- degree about the axis showed above.

Case 2 For the sequence $\left[a_1,\mathrm{....}{a}_n,a_n,\mathrm{....}{a}_1\right]$ , there exists a block in middle the snake. It is easy to check if we rotate this block like Figure 7, the overall shape of the snake does not change.

Figure 7 Case 2.

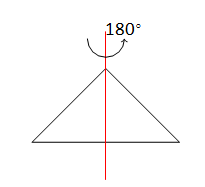
Therefore, we have proved this theorem works well for any snake not forming a closed loop. Then we will discuss about the closed loop. It is easy to see the above argument still works for loops with the form $\left[a_1,\mathrm{....}{a}_{n-1},a_n,a_{n-1},\mathrm{....}{a}_1\right]$ or $\left[a_1,\mathrm{..}{a}_n,a_n,\mathrm{...}{a}_1\right]$ . When we discuss the loops $\left[a_1,\mathrm{...}{a}_{n-1},a_n,a_{n-1},\mathrm{...}{a}_2\right]$ or $\left[a_1,\mathrm{...}{a}_n,a_n,\mathrm{....}{a}_2\right]$ , we can just ignore a₁, and we can see the other part of these sequence have already determined a unique closed loop snake that we could apply the above argument on. Although the theorem above covers the general angle rotation case, below we make the assumption of integer multiple of 90 degree rotations. Normally in shape design using the Rubik’s Snake, this assumption is valid. A block in a Rubik’s Snake is half of a unit cube. Therefore it can be embedded into a unit cube. For convenience, we place a Rubik’s Snake on a 3D coordinate system such that the center of the blocks has integer coordinates.

We will consider different types of sequences to study a snake. Since the center of each block is placed on integral coordinates, we always add one of <±1, 0, 0>, <0, ±1, 0>, <0, 0, ±1> to go from one block to the next. We use “+x” to mean “add (1, 0, 0)” and “-x” to mean “add (−1, 0, 0)”. Similar notations will be used for +y, −y, +z, −z. We call the sequence generated by this way the shift sequence. By removing the signs in the shift sequence, we call it the shift sequence without signs.

For a shift sequence, if the first and last elements are different, then we can form a loop, although it is not necessarily a snake loop.

Lemma 5

Given a snake whose degree sequence contains at least one odd degree. Then by removing the element in the shift sequence corresponding to an odd degree will gives us a shift sequence for a new snake. The parity of the sum of the degree minus the length remains unchanged.

Proof: We can assume that the shift sequence is in form of “...xyz...” where y corresponds to an odd degree. Then we can go over all cases of removing y to argue that it will not change the parity.

Given a closed loop snake. If we keep removing odd degrees until there is no more odd degree, then we get a snake with the length to be even and the sum of degrees to be even. Reverse the process, we rediscover the result from¹³ that the sum of degrees is even for a closed loop with integer multiple of 90 degree rotations. In,¹³ the Möbius strip for a Rubik’s Snake are defined. The equivalent condition is also proved in¹³ that for a closed loop snake with integer multiple of 90 degree rotations to be a Möbius snake, the sum of degrees is of the form $4k+2$ . Now we are ready to present the main results of this paper in the following theorems.

Theorem 6

A palindromic closed loop snake of type I has 4k blocks for some .

Proof: Let the snake sequence be in form of “a......dd......a”. Place the middle block (determined by “dd”) at the origin with the direction such that the two square faces locate on the xz- and yz-plane, respectively. Then $y=x$ is an axis of symmetry. Such axis must pass through the center of the middle block determined by “aa”. We may assume that center to be $\left(a,a,0\right)$ for some integer a. By Theorem 1, the parity of the number of blocks from $\left(0,0,0\right)$ to $\left(a,a,0\right)$ is same as $2a+1$ . So, we may assume that there are $2b+1$ blocks from $\left(0,0,0\right)$   $\left(a,a,0\right)$ for some integer b. For the closed loop, there are $\left(2b+1\right)+\left(2b+1\right)-2=4b$ blocks. This completes the proof.

Theorem 7

Given a Type II palindromic closed loop snake that is in form of “a......b......”.

1. If both a and b are even, then the snake is either non-Möbius with 4k blocks or Möbius with $4k+2$ blocks for some integer k.
2. If both a and b are odd, then the snake is non- Mö

Proof: We use the result from Lemma 5 in the argument below. In the shift sequence, the variables at the locations of “a” and “b” must be the same (although the sign could be different). We may assume that the variable is “z”. Keep removing pair of odd degrees except for the locations of “a” and “b” until there is no more odd degree except for those two locations.

1. If a and b are even, then there is no odd degree. For the resulting snake, the shift sequence without signs must be in form of “[zx zx]*2”. Both the sum of degrees and the number of blocks are multiple of 4. Reverse the process, we see that if the number of blocks is multiple of 4, then the sum of degree is multiple of 4 and so the snake is non-Mö Otherwise, if the number of blocks is in terms of , then the sum of degree is in terms of and so the snake is Möbius.
2. If a and b are odd, then the resulting shift sequence without sign is in form of “zx...zxzy...zy”

where the first part is “zx” repeating and 2nd part is “zy” repeating. We have two cases.

Case 1 If the two opposite “z” have the same signs. Then the resulting snake has sum of degree and length to be multiple of 4. Reverse back to the original snake, the length has to be for some in order to cancel out all the “z”s. So the sum of degree is a multiple of 4 and the snake is non-Möbius.

Case 2 If the two opposite “z” have opposite signs. Then the resulting snake has length as multiple of 4 and sum of degrees as $4k+2$ for some $K\in Z$ . Reverse back to the original snake, the length has to be $4a+2$ for some $a\in N$ and so the sum of degree is a multiple of 4. The snake is non-Möbius.

Theorem 8

Any palindromic period 2 snake is non-Möbius with 4k blocks for some $k\in N$ .

Proof: Given a palindromic period 2 snake. We will argue by the types of the snake.

Case 1 Assume the snake is type I. By Theorem 6, the number of blocks is a multiple of 4. Since it is period 2, it has to be in form of “d...dd...d”. Since the number of blocks is a multiple of 4, it cannot be in form of “d...e...dd...e...d”. The snake must be in form of “d...ee...dd...ee...d”. In this case, sum of degrees must be a multiple of 4 and so it is non-Möbius.

Case 2 Now assume the snake is type II. We will do the proof by contradiction. Assume on the contrary that the snake is Möbius or has $4k+2$ blocks for some $K\in N$ . By Theorem 7, in order to have a Möbius snake, the number of blocks must be $4t+2$ for some $t\in N$ . So, we can assume that the snake has $4k+2$ blocks. Since the snake is period 2 and palindromic, it has to be in form of “a...ee...a...ee...”. The form of “ee...ee...” indicates that the snake is also a palindromic snake of type I. So, the number of blocks is a multiple of 4, a contradiction.

Lemma 9

Given a closed loop period 3 snake. Let $S_1$ , $S_2$ ,$S_3$ be the 3 parts of a shift sequence corresponding to the 3 repeating degree sequences. Then $S_2$ can be obtained from $S_1$ by a rotation of $\left(u,v,w\right)$ such that $\left\{\left|u\right|,\left|v\right|,\left|w\right|\right\}=\left\{x,y,z\right\}$

Proof: In¹³, we proved in Theorem 7 that the period of a closed loop Rubik’s Snake with integer multiple of 90 degrees cannot exceed 4. In that proof, we can see the period 3 case corresponds to the following map: x, y $S_1$ in is mapped to ±y, ±z or ±z, ±x in $S_2$ (8 sub-figures of snake blocks embedded in cubes in¹³ that corresponds to period 3 case). Cross product is mapped to cross product. In the end, x, y, z is mapped to a rotation of it with even number of negative signs among the three images.

Theorem 10

There is no palindromic period 3 Möbius snake of type II.

Proof: Given a type II palindromic period 3 snake. Then the degree sequence is of the form “...d...e...d...e...d...e”. By Lemma 9, we may assume that the corresponding shift sequence without sign is in form of “...x...u...y...v...z...w” such that u, v, w is a rotation of x, y, z. Note that it can be proved by induction that, if d is even, then the corresponding shift sequence without sign is also palindromic from the corresponding position. Since such sequence is not palindromic from x, it means the corresponding degree d is odd. Similarly, e is also odd. By Theorem 7 (b), the snake is non-Möbius.

Theorem 11

Any palindromic period 3 Möbius snake has 12k blocks for some $k\in N$ .

Proof: Given a palindromic period 3 Möbius snake. By Theorem 10, the snake must be type I. By Theorem 6, the number of blocks is a multiple of 4. Since the snake is period 3, the number of blocks is also a multiple of 3, and so a multiple of 12.

In¹³, a complete list of 17 different (different in overall shape, left and right hand are considered to be the same) period 3 Möbius snakes with 36 blocks with palindromic property was provided. Our Theorem 10 shows that they must all be of Type I. Here, we present a complete list of 15 different periods 3. Rubik’s Snakes with 36 blocks with Type II palindromic property in Figure 8. Our theorem 10 shows they cannot be Möbius. In addition, there are 22 different period 3 Rubik’s Snakes with 36 blocks with Type I palindromic property that are not Möbius.

Figure 8 A complete list of period 3 Rubik’s snakes with 36 blocks with type II palindromic property.

The Rubik’s Snake is a good model for studying protein folding and the construction of reconfigurable modular robots. To design interesting shapes using the Rubik’s Snakes, we first developed some theorems related to palindromic, periodic and Möbius Rubik’s Snakes. With the guidance of the theories, we are able to search for beautiful ways of folding the Rubik’s Snake.

We thank Dr. Zilong Li for interesting discussions. S. Hou’s research is partially supported by the Walter Koss Endowed Professorship. The title of the professorship is made available through the State of Louisiana Board of Regents Support Funds.

The authors declare that they have no conflicts of interest.

None.

1. Fiore A. Shaping rubik’s snake. Penguin Books, Harmondsworth, Middlesex, England. 1981.
2. Iguchi K. A toy model for understanding the conceptual framework of protein folding: rubik’s magic snake model. Mod Phys Lett B. 1998;12(13):499–506.
3. Iguchi K. Exactly solvable model of protein folding: rubik’s magic snake model. Int J Mod Phys B. 1999;13(4):325–361.
4. Ding X, Lu S, Yang Y. Configuration transformation theory from a chain type reconfigurable modular mechanism-rubik’s snake. The 13th world congress in mechanism and machine science. 2011.
5. Zhang X, Liu J. Prototype design of a rubik snake robot. Mechanisms and Machine Science. 2016;36.
6. Liu J, Zhang X, Zhang K, et al. Configuration analysis of a reconfigurable rubik’s snake robot. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. 2019;233(9):3137–3154.
7. Detmvit J, Hartenberg R. A kinematic notation for lower-pair mechanisms based on matrices. ASME Journal of Applied Mechanics. 1995:215–221.
8. Yim M, Roufas K, Duff D, et al. Modular reconfigurable robots in space applications. Autonomous Robots. 2013;14(2–3):225–237.
9. Zhang X, Liu J, Feng J, et al. Effective capture of nongraspable objects for space robots using geometric cage pairs. IEEE/ASME Transactions on Mechatronics. 2020;25(1):95–107.
10. Hull TC, Belcastro SM. Modelling the folding of paper into three dimensions using affine transformations. Linear Algebra and its applications. 2002;348(1–3):273–282.
11. Tachi T. Simulation of rigid origami. Origami. 2020;4(08):175–187.
12. Li Z, Hou S, Bishop T. Computational design and analysis of a magic snake. J Mech Rob. 2020;12(5):054501.
13. Hou S, Chen Y, Li Z. Some mathematical problems related to the rubik’s snake. J Mech Rob. 2021;13(1):014502.