The original control problem of optimal reorientation from a state of rest to a state of rest is considered and solved. The control function is torque vector. Problem of optimal control is investigated in detail for statement when control is restricted and the used functional of optimality includes kinematical rotary energy and time of maneuver. For solving and synthesis of the optimal control program, the quaternion method and the Pontryagin’s maximum principle are applied. Analytic solution of the proposed problem is presented basing on the differential equation connecting the angular velocity vector and quaternion of spacecraft attitude. It is shown that a chosen criterion of optimality provides a turn of a spacecraft with rotation energy which does not exceed the required value. This property of proposed control increases safety of flight. The time-optimal problem was solved also. The control law is formulated in the form of an explicit dependence of the control variables on the phase coordinates. All key expressions and equations are written in quaternion form which is convenient for onboard realization and implementation. The analysis of the special control regime of the spacecraft was made. Analytical formulas were written for duration of acceleration and braking. For specific cases of spacecraft configurations (dynamically symmetric spacecraft and spheric-symmetrical spacecraft as particular cases), complete solution of optimal control problem in closed form is given. Numerical example and the results of mathematical simulation for spacecraft motion under optimal control are demonstrated. This data supplements the made theoretical descriptions, and illustrates the practical feasibility of the designed algorithm for controlling the spatial orientation of the spacecraft showing reorientation process in visual form.

Keywords: attitude, quaternion, reorientation, optimal control, criterion of optimality, maximum principle

The optimal control problem of spacecraft reorientation from arbitrary known initial attitude into the required angular position was solved. Spacecraft motion around the center of mass is given by quaternion of attitude.¹ Designing the optimal rotation program is based on quaternion models, Pontryagin’s maximum principle, and universal variables.² In present time, spacecrafts are used in many areas of industry and scientific occupations. For example, astrophysical researches and other scientific discoveries would be impossible without spacecrafts for which success of mission and duration of performance in a working point of orbit (orbital position) are determined by successful control of motion, by an efficiency of attitude control (an improved system of spacecraft attitude is especially important for the spacecrafts with instruments and devices for astronomy measurements and for satellites of Earth supervision).^3–5 In particular, in April 2018, NASA launched the Transiting Exoplanet Survey Satellite (TESS), a space telescope that helps to study the exoplanets, or NASA’s James Webb Space Telescope measuring atmospheric properties and compositions of small planets, and also Atmospheric Remote-sensing Infrared Exoplanet Large-survey (ARIEL) space telescope of European Space Agency.⁵

Many works have been dedicated to investigating optimal solutions in problems of controlling the angular position of a rigid body.^1,6–26 Most solutions correspond for the case when the spacecraft rotates around a motionless axis^1,6–10 (including the use the algorithm of fuzzy logic⁷ or the method of the inverse dynamic problem),⁸ time-optimal maneuvers is topical also.^1,9–14 Particular solutions were found obtained for axi-symmetric spacecraft.^14–16 For the spacecraft with arbitrary mass distribution, an analytical solution to the three-dimensional turn problem with arbitrary boundary conditions for spacecraft’s angular position is not known except some special cases of reorientation problem.¹ An analytical solution to the optimal turn problem in a closed form, if it were obtained, is of great practical interest, since it allows the finished laws of programmed control and variation of the optimal trajectory of spacecraft motion to be applied onboard of the spacecraft.^11,17 Principal difference of the presented research work consists in use of new minimized index which characterizes consumption of energy and time for spacecraft reorientation and combines the duration of maneuver and integral of kinetic rotation energy. Issues of cost-efficiency also remain relevant for the time being for spacecraft motion control. The method designed in present article is universal control; it does not depend on a ratio (proportion) of moments of inertia or final position of a spacecraft. Also, the developed algorithm is useful for of control of the spacecrafts with inertial actuators (specific features of system with gyrodins were considered earlier).^18–21

Formulation of optimization problem

Spacecraft’s angular rotation around the center mass is determined by the dynamic equations:⁶

$J_1{\dot{\omega }}_1+\left(J_3-J_2\right){\omega }_2{\omega }_3=M_1,J_2{\dot{\omega }}_2+\left(J_1-J_3\right){\omega }_1{\omega }_3=M_2,J_3{\dot{\omega }}_3+\left(J_2-J_1\right){\omega }_1{\omega }_2=M_3$   (1)

where J_i are the spacecraft’s principal central moments of inertia, M_i are projections of torque M onto the principal central axes of the spacecraft’s inertia ellipsoid (these axes form body basis E), are projections of the absolute angular velocity vector ω onto the axes of the body basis E (i= $\overline{1,3}$ ). The mathematical formalism of quaternions (the Euler–Rodrigues parameters) is used for describing the spatial motion of a spacecraft. Angular orientation of the spacecraft coordinate system is defined relative to the reference basis I which we assume inertial coordinate system. Motion of the body basis E relative to the reference basis I will be specified by the quaternion Λ.¹ We assume that the quaternion Λ is normalized (||Λ||=1), and the basis I is inertial. Therefore, the following kinematic equation is true

$2\dot{\Lambda }=\Lambda o\omega$   (2)

The symbol is a sign of multiplication of quaternions. For simplicity, the quaternion specifying the current spacecraft orientation is assumed the normalized quaternion (||Λ ||= 1). The spacecraft motion control relative to its center of mass is done by changing the torque M (external or internal, if spacecraft orientation control is done with use of inertial actuators, i.e. powered gyroscopes). Region of admissible values for the vector M is determined by the condition

$M_1^2/J_1+M_2^2/J_2+M_3^2/J_3\le u_0^2$   (3)

where u₀>0 is positive value specifying power of actuators. Angular positions of the initial and final spacecraft attitude are given by the quaternions L_in & L_f respectively. In many practical modes of reorientation, initial state satisfies condition ω (0)=0 and final angular velocity must be absent ω (T)=0 (these cases occur very frequently, especially if attitude control is done relative to inertial coordinate system). The boundary conditions are:

$\Lambda (0)={\Lambda }_{\text{in}}$ , ω (0)=0  (4)

$\Lambda (T)={\Lambda }_{\text{f}}$ , ω (T)=0  (5)

where T is the time of ending the reorientation process, and the quaternions ${\Lambda }_{\text{in}}$ and ${\Lambda }_{\text{f}}$ which specify the orientation of spacecraft-bound axes at the initial and final time instants have arbitrary predefined values satisfying the condition ||${\Lambda }_{\text{in}}$ ||=||${\Lambda }_{\text{f}}$ ||=1. We estimate efficiency of control using the index

$G=T+k_0{\displaystyle \underset{0}{\overset{T}{\int }}(J_1{\omega }_1^2+J_2{\omega }_2^2+J_3{\omega }_3^2)dt}$   (6)

where k₀ > 0 is the constant positive coefficient; Т is the time of ending the turn.

The reorientation optimal control problem is formulated in following statement: spacecraft must be transferred from state (4) into state (5) according to equations (1), (2) and restriction (3) with minimal value of the functional (6) (time T, when the spacecraft reorientation maneuver should end, is not fixed, and it is optimized simultaneously with value G). The solution М(t) is sought in the class of piecewise continuous functions. The chosen criterion of optimality guarantees the spacecraft’s motion with a kinetic energy of rotation not exceeding the required value (it provides turn of a spacecraft with the bounded rotation energy because the coefficient k₀ ≠ 0). It allows for estimation of an energetically advantageous angular motion trajectory along which the spacecraft will turn from its initial position L_in into the required final angular position L_f, and for finding the corresponding control mode. Presence of time factor in the assumed index (6) limits the duration T of the optimal turn to some finite time T_opt.

Solution procedure of the optimal control problem

The formulated control problem (1)–(6) is a classical dynamic problem of the optimal turn,¹ and the torques М_i are the control variables, and angular velocity projections ${\omega }_i$ are controllable variables (for minimization of index (6)). For solving the formulated problem, we use Pontryagin’s maximum principle.²⁷ The restriction on the phase variables L is insignificant, since it is satisfied during any motions relative to the center of mass; ||Λ(t)||=const due to equation (2); we assumed ||Λ(0)||=||Λ_in||=1, and therefore ||Λ(t)||=1 at any time tÎ[0, T]. Introduce the conjugate variables ${\varphi }_i$ corresponding to the angular velocities ${\omega }_i$ (i= $\overline{1,3}$ ). The minimized functional (6) does not include the position coordinates, therefore we use universal variables r_i,² and to introduce the conjugate variables corresponding to the phase variables (components of quaternion Λ) is not obligatory. The Hamiltonian H of problem (1)-(6) looks like the following:

H = j₁ ( М₁ + (J₂ - J₃ )w₂ w₃ ) /J₁ + j₂ ( М₂ + (J₃ - J₁ )w₁ w₃ ) /J₂ + j₃ ( М₃ + (J₁ - J₂ )w₁ w₂ ) /J₃ +
${\omega }_1{r}_1+{\omega }_2{r}_2+{\omega }_3{r}_3$ +     (7)

where the functions r_i and λ_j are related by the following relations:²

$r_1=({\lambda }_0{\psi }_1+{\lambda }_3{\psi }_2-{\lambda }_1{\psi }_0-{\lambda }_2{\psi }_3)/2$ ,
$r_2=({\lambda }_0{\psi }_2+{\lambda }_1{\psi }_3-{\lambda }_2{\psi }_0-{\lambda }_3{\psi }_1)/2$ ,
$r_3=({\lambda }_0{\psi }_3+{\lambda }_2{\psi }_1-{\lambda }_3{\psi }_0-{\lambda }_1{\psi }_2)/2$

and ${\psi }_j$ are the conjugate variables corresponding to components of quaternion ${\lambda }_j$ (j= $\overline{0,3}$ ).

The first terms (they contains the conjugate variables ${\varphi }_i$ ) comprise the dynamical part of the Hamiltonian H, the second terms (they contains universal variables r_i) comprise the kinematical part of the Hamiltonian H which is responsible for the geometric properties of optimal motion. Other terms corresponds to the chosen optimality criterion. The function H does not take into account the phase constraint ||Λ||=1, since || Λ(0)||=1. For the universal variables r_i, the following system of equations are true:²

${\dot{r}}_1={\omega }_3{r}_2-{\omega }_2{r}_3,{\dot{r}}_2={\omega }_1{r}_3-{\omega }_3{r}_1,{\dot{r}}_3={\omega }_2{r}_1-{\omega }_1{r}_2$   (8)

Change in vector r formed by the universal variables r_i is solution of the following equation

$\dot{r}=-\omega \times r$

(it is vector form of the equations (8) if variables r_i is assumed as assume projections of vector r on the axes of the body basis E.²  The symbol × denotes the vector product of two vectors. It is know that the vector r turns out to be motionless relative to the inertial basis I, and |r|=const¹0.² The equations for conjugate variables ${\varphi }_i$  have the form

${\dot{\varphi }}_i=-\frac{\partial H}{\partial {\omega }_i}$

The conjugate system of equations is

$\begin{array}{l}{\dot{\varphi }}_1=2k_0{J}_1{\omega }_1-{\omega }_3{n}_2{\varphi }_2-{\omega }_2{n}_3{\varphi }_3-r_1,\\ {\dot{\varphi }}_2=2k_0{J}_2{\omega }_2-{\omega }_3{n}_1{\varphi }_1-{\omega }_1{n}_3{\varphi }_3-r_2,\\ {\dot{\varphi }}_3=2k_0{J}_3{\omega }_3-{\omega }_2{n}_1{\varphi }_1-{\omega }_1{n}_2{\varphi }_2-r_3\end{array}$    (9)

where n₁ = (J₂ – J₃ )/J₁ , n₂ = (J₃ – J₁ )/J₂ , n₃ = (J₁ – J₂ )/J₃ are the constant coefficients.

Thus, the problem of finding an optimal control is reduced to solving the system of equations of spacecraft’s angular motion (1), (2), and equations (8), (9) under the condition that the control itself is chosen by maximizing the Hamiltonian. The optimal function r(t) is calculated through the quaternion (t) using the formula:^1,2

$r=\tilde{\Lambda }\circ c_E\circ \Lambda$ , where c_E= ${\Lambda }_{\text{in}}\circ r(0)\circ {\tilde{\Lambda }}_{\text{in}}$ =const

($\tilde{\Lambda }$ is the quaternion conjugate to quaternion Λ). The direction of vector c_E depends on the initial and final spacecraft positions. In order for the spacecraft to have the required orientation at the right-hand end $\Lambda (T)={\Lambda }_{\text{f}}$ , the vector c_E (or the value of vector r at the initial instant) by the corresponding solution of equation (2) should be determined. The system of differential equations (8), (9), together with the maximality condition of the Hamiltonian H, is necessary conditions of optimality. Constraint equations are given by the system of equation (2) which describes the spacecraft’s motion relative to its center of mass. The maximum conditions of function H determine sought solution M(t). Boundary position conditions Λ(0) and Λ(T) determine solutions Λ(t) and r(t). The boundary problem of the maximum principle is to find the value of the vector r(0) for which the solution of the system of differential equations (1), (2), (8), (9) together with simultaneous maximization, at every current moment of time, of the Hamiltonian H satisfies reorientation conditions (4), (5).

In the problem being solved, the time of the spatial turn is not fixed; therefore, the following transversality condition H=0 must be satisfied²⁸ (since the Hamiltonian H does not explicitly depend on time). The system of to equations (8), (9), together with the requirement of maximality of the Hamiltonian H and the conditions r(0)≠0, H=0, are the necessary conditions of optimality. To find the control function M(t) (the optimal control program) and the optimal vector r, we define the conditions for the maximality of the Hamiltonian H, which we rewrite in the form

H = φ₁М₁ /J₁ + φ₂М₂ /J₂ + φ₃М₃ /J₃ + H_inv

where H_inv does not explicitly depend on the control functions M_i . Let φ be the vector with components φ_i. If φ=;0, the maximum of the function H for the controls М_i (t) under restriction (3) is achieved when

M_i = $\frac{u_0{\varphi }_i}{\sqrt{{\varphi }_1^2/J_1+{\varphi }_2^2/J_2+{\varphi }_3^2/J_3}}$    (10)

(the case of φ=0, in which the Hamiltonian does not explicitly depend on the control M, requires additional consideration). Further we will demonstrate that M=0 if Φ=0 (and φ = 0). The optimal solution is determined by the closed system of equations (1), (2), and (8)-(10) considering the conditions (4) and (5). Let us find the characteristic properties of the optimal motion using the normalized vector р = r/|r|, |p|=1 (due to the fact that |r| =const=|r(0)|¹0). For the vector p, we have $\dot{p}=-\omega \times p$ , or

${\dot{p}}_1={\omega }_3{p}_2-{\omega }_2{p}_3,{\dot{p}}_2={\omega }_1{p}_3-{\omega }_3{p}_1,{\dot{p}}_3={\omega }_2{p}_1-{\omega }_1{p}_2$   (11)

In what follows, the components p_i of the vector p will be used. Note that r_i=|r(0)|p_i. The solution to the system of equations (1) and (8)-(10) (under the requirement ω (0) =  ω (Т) = 0) has the form

${\varphi }_i=a(t)p_i$   (12)

$J_i{\omega }_i=b{p}_i$   (13)

where b is a scalar value; а(t) is scalar function of time with £0 (b³0 for optimal motion ω (t)).

After substituting solution (12), (13) into system (9) and considering the equations (11) for the derivatives , we obtain the identity expressions if p=(2k₀b – r₀)p, where r₀=|r(0)|. Therefore, the optimal functions а(t) and b(t) satisfy the condition =2k₀b – r₀ (since |p|¹0), from which two features follow: $\dot{a}$ (0)= $\dot{a}$ (T)= –r₀ and b(0)=b(T)=0 (due to the requirement ω (0) =  ω (Т) = 0). At initial instant t=0, а(0)>0; otherwise M×p<0 and b<0 due to the equations (1), (10), (12), and <0, a<0 for any t>0. However, in such a scenario (when а (0)£0), the switching is absent (since b<0 and $\dot{a}$ <0); the torque М acts in one direction, spinning the spacecraft until ω→∞. Accordingly, at end of reorientation maneuver, condition M×L<0 is necessary (and M×p<0 also) and а (T)<0. The scalar function a(t) is the continuous function of time. Therefore, moment of time when a(t)=0 exists. If $\dot{a}$ =0 then a(t)=0,Φ=0, φ=0 (otherwise the value a(t) does not change a sign, i.e. a(t)>0 and M×L>0 during interval of control [0, T], but such rotation does not satisfy the condition ω (T)=0); L is angular momentum of a spacecraft (the multiplication sign × means the scalar product of vectors).

From (1) and (13), we have$\dot{b}$ = M×p. If a(t)>0, we have acceleration process. If a(t)<0, we have braking. For acceleration phase [0, t₁], we have $\ddot{a}$ >0; for braking [t₂, T], we have $\ddot{a}$ <0 (since $\ddot{a}$ =2 $\dot{b}$ ). For functions a(t) and b(t), we have the following properties: a(Т-t)= -a(t) and b(Т-t)=b(t).

The equalities (12), (13) are satisfied together. For spin-up, optimal controlling moment M is calculated by the formula

$M_i=u_0{J}_i{\omega }_i/\sqrt{J_1{\omega }_1^2+J_2{\omega }_2^2+J_3{\omega }_3^2}$   (14)

Optimal torque M and angular momentum L are parallel during acceleration phase. Differentiation of left and right parts of equalities (14) gives the following differential equations (angular accelerations ${\dot{\omega }}_i$  are taken from dynamic equations (1)):

${\dot{M}}_1={\omega }_3{M}_2-{\omega }_2{M}_3,{\dot{M}}_2={\omega }_1{M}_3-{\omega }_3{M}_1,{\dot{M}}_3={\omega }_2{M}_1-{\omega }_1{M}_2$   (15)

Rewrite last equations in vector form

$\dot{{\rm M}}=-\omega \times {\rm M}$

The obtained differential equation, for the controlling moment M, means its immobility relative to inertial coordinate system. As consequence, |M|=const during acceleration stage. For optimal braking, the torque M is

$M_i=-u_0{J}_i{\omega }_i/\sqrt{J_1{\omega }_1^2+J_2{\omega }_2^2+J_3{\omega }_3^2}$   (16)

After differentiation of equalities (16) we obtain differential equations (15) from which the property |M|=const appears for the entire braking stage. Thus, equality |M|=const is satisfied for optimal rotation during acceleration and braking phases. It is very important property of optimal motion and optimal control. Both at imparting the calculated angular momentum, and at damping of rotation, the torque M has a constant magnitude (direction of vector M is not changed relative to inertial basis I); i.e. within acceleration and braking segments, optimal torque M is the fixed vector relative to inertial coordinate system. If relations (13) are fulfilled, then  $p_1^2/J_1+p_2^2/J_2+p_3^2/J_3=\text{const}$

To be certain of this, we differentiate the left-hand part of the given equality with respect to time considering the equations (11) for p_i and the dependences (13) for components w_i of angular velocity.

$p_1{\dot{p}}_1/J_1+p_2{\dot{p}}_2/J_2+p_3{\dot{p}}_3/J_3$ = w₁p₂p₃ /J₃ - w₁p₂p₃ /J₂ + w₁p₂p₃ /J₂ - w₂p₁p₃ /J₃ + w₂p₁p₃ /J₃ - w₁p₂p₃ /J₃ º 0

For optimal solution (12), the dependences (10) can be rewritten in the form

M_i = $\frac{u_0\text{sign}a(t)p_i}{\sqrt{p_1^2/J_1+p_2^2/J_2+p_3^2/J_3}}$

Thus, when a(t)≠0 and j≠0, the statement |M|=const≠0 is true, and, therefore, $\dot{b}$ =const, as well. The torque M satisfies the condition (3). Therefore, we can write the following relation

M=m₀signa(t)p , where m₀=u₀/C $C=\sqrt{p_1^2(0)/J_1+p_2^2(0)/J_2+p_3^2(0)/J_3}$ ,

For time interval when a(t)=const=0, the system (9) is transformed to the equations $2k_0{J}_i{\omega }_i-r_i=0$ , and the relations

${\omega }_i=r_i/(2k_0{J}_i)$   (17)

are satisfied. Let us find the controlling moments necessary to support the spacecraft’s optimal rotation mode in time interval t₁<t<t₂ during the rotation with a(t)=const=0. This situation is named special control regime, since the Hamiltonian does not explicitly depend on the controlling moments, and control functions M_i cannot be found from the condition of maximality for function H when a(t)=const=0 and φ=const=0. But we can calculate optimal values M_i using (17). Let us substitute the functions ${\omega }_i$ (t) computed by expressions (17) into dynamic equations (1) with taking into account the fact |r| =const¹0. As result, all components of torque M are M_i=0. Thus, between acceleration phase and braking of spacecraft rotation, we have M=0 and b(t)=r₀/(2k₀). This follows from the analysis of equations (17) that show a relation between the angular momentum L and the vector r of universal variables. The fact that L=r/(2k₀) and |L|=const, keeping in mind the immobility of vector r in the inertial basis I, implies that the spacecraft’s angular momentum vector is constant relative to inertial coordinate system during the reorientation. The kinetic energy E_k is constant also (${\dot{E}}_k=\omega \cdot {\rm M}$ since M=0).

From formula (13), we see that b=|L|. Left-hand sides of equations (13) are projections of the spacecraft’s angular momentum vector onto the axes of the body basis E. Expressions (13) lead to the conclusion that spacecraft rotation during optimal motion is done with a constant direction of angular momentum relative to the inertial coordinate system. The value of b equals the modulus of the spacecraft’s angular momentum L. The triple p₁, p₂, p₃ represents directional cosines of the vector L relative to the axes of the basis E. Equations (13) clearly demonstrate that in the geometric representation, the vector p is simply the unit vector of the spacecraft’s angular momentum vector L in the spacecraft’s coordinate system. Thus, the optimal (in the sense of minimizing the functional (6)) spacecraft reorientation is performed along the “trajectory of free motion”. Equations (11), together with equalities (13), form a closed system of equations which determine unique properties of optimal motion. The optimal function b(t) is a non-negative piecewise-linear function of time. At t=0 and t=T, b(t)=0; at t=t₁ and t=t₂, b(t)=r₀/(2k₀). The time T equals T=t₂+t₁ (since |M|=m₀ for acceleration segment and segment of braking, and t₁=r₀ /(2k₀m₀). Concrete solution is determined by close this system of equations (11), (13) by equation (2) with conditions (4), (5) for solution Λ(t).

Here and in what follows, it is assumed that the “trajectory of free motion” is a multitude of angular positions (the values of L) that a rigid body occupies during its rotation by inertia. In the geometric interpretation, the “trajectory of free motion” is a trace of the representing point Λ (t), where Λ (t) is a solution of the system of differential equations (1), (2) when M₁=M₂=M₃=0 and ${\omega }_{\iota }$ ≠0. Let us find the proportion between the kinetic energy E_k and angular momentum L during optimal slew maneuver. The kinetic energy E_k and the value b are related by expression

$E_k=b^2(p_1^2/J_1+p_2^2/J_2+p_3^2/J_3)/2$

Therefore, the proportion $E_k/{\left|L\right|}^2=(p_1^2/J_1+p_2^2/J_2+p_3^2/J_3)/2$ =const.

For segments when a(t)≠0 and M≠0, we have ${\left|M\right|}^2=u_0^2{\left|L\right|}^2/(2E_k)$  (see formulas (14), (16)), i.e. $E_k/{\left|L\right|}^2=u_0^2/(2{\left|M\right|}^2)=\text{const}$ (since |M|=const=m₀ if a(t)≠0). If a(t)=0, then M=0, |L|=const and E_k=const. The quantities |L| and E_k are the continuous functions, therefore, E_k/|L|² is continuous function of time, and it is constant within all three segments of control. Thus, it is shown that this proportion E_k/|L|² is constant on the entire motion interval 0≤t≤T. It is key property of optimal motion for criterion (6), E_k/|L|²=const.

The Hamiltonian H is independent of time in explicit form, therefore, H=const inside the entire interval of control 0≤t≤T.²⁸ From the formula (7), the equality

${\omega }_1{r}_1+{\omega }_2{r}_2+{\omega }_3{r}_3-k_0(J_1{\omega }_1^2+J_2{\omega }_2^2+J_3{\omega }_3^2)-1$ =const

is obtained for time interval when φ=0 (i.e. in special control regime). After substitution the values ${\omega }_i$ calculated by equations (17) in this equality (taking into account the equalities r_i=r₀p_i), the conditions

$r_1^2/J_1+r_2^2/J_2+r_3^2/J_3=\text{const}$ , and $p_1^2/J_1+p_2^2/J_2+p_3^2/J_3=\text{const}$

are satisfied for the moments of time when a(t)=0 because |r| =const (at segments of acceleration and braking, the above mentioned conditions are satisfied automatically, it follows from the equations (14), (15), (16)).

Thus, the problem of constructing the optimal control ω(t) has been mainly reduced to finding such a value of vector p(0) that as a result of the spacecraft’s motion, according to equations (2), (11), and (13) with initial conditions (4), the equalities (5) will be satisfied. It is virtually impossible to find a general solution of this system of equations. The problem is to find boundary conditions on p(0) and p(T) which are related by expression

${\Lambda }_{\text{f}}\circ p(T)\circ {\tilde{\Lambda }}_{\text{f}}={\Lambda }_{\text{in}}\circ p(0)\circ {\tilde{\Lambda }}_{\text{in}}$   (18)

The time of ending the reorientation process is not fixed, therefore H(T)=0; the Hamiltonian H is independent of time in explicit form, hence, H=0 inside the entire interval of control 0≤t≤T.²⁸ Maximum value of the kinetic energy E_k and modulus of angular momentum (and values a(0) and r₀) are determined by condition H=0. At instant t=0, angular velocity is zero, the function H is equal to

$m_{0}a(0)(p_1^2/J_1+p_2^2/J_2+p_3^2/J_3)-1=0$

Hence, the value a(0) for optimal function a(t) is a(0)= 1/(u₀C). Accordingly, a(T) is a(T)= –1/(u₀C). At instants when a(t)=0, the function H is

$r_{0}b(p_1^2/J_1+p_2^2/J_2+p_3^2/J_3)-k_0{b}^2(p_1^2/J_1+p_2^2/J_2+p_3^2/J_3)-1=0$

and b=r₀/(2k₀) if $\dot{a}$ =0 (this follows from (17)). From last equation, we find the optimal value $r_0=2\sqrt{k_0}/C$ . It is obvious that modulus of angular momentum |L| has maximal value L_max between acceleration and braking.

Thus, L_max is determined unambiguously $L_{\max }=1/(C\sqrt{k_0)}$ . The found magnitude L_max corresponds to the maximal kinetic rotation energy E_max= 1 /(2k₀). Respectively, $t_1=1/(u_0\sqrt{k_0})$ if phase of uncontrolled motion (when M=0) is not absent.

Note, the vectors ω and p are related as

${\omega }_i=\frac{\sqrt{2E_k}}{\sqrt{p_1^2/J_1+p_2^2/J_2+p_3^2/J_3}}\cdot \frac{p_i}{J_i}$   (19)

The task of the onboard control system for realization of optimal control is to impart the initial motion conditions to the spacecraft (namely the calculated angular velocity at time moment t=0) and to suppress the kinetic energy to zero at time moment t=T, when $\Lambda (t)={\Lambda }_{\text{f}}$ (after the spacecraft reaches its final position ${\Lambda }_{\text{f}}$ ).

From the moment of reaching the necessary initial angular velocity ${\omega }_{\text{cal}}$ and until the reorientation is finished, when the spacecraft will be in the neighborhood of the required position ${\Lambda }_{\text{f}}$ , there is no torque M acting on the spacecraft’s body; the spacecraft performs uncontrolled rotation (M=0), i.e. free motion. Creating the initial angular velocity and damping the final rotation happens in an impulse (as fast as the spacecraft’s actuators will allow). Between the imparting of angular momentum and the suppressing of angular momentum we have (if special control regime is present):

$J_1^2{\omega }_1^2+J_2^2{\omega }_2^2+J_3^2{\omega }_3^2={\text{const}}_{}$ = 1 /(k₀C) ,  = 1 / k₀   (20)

(these equalities (20) follow from condition Н=0 and dependences (7), (17)).

Main types of optimal control

In many practical tasks, reorientation is made in situation when initial state satisfies condition (0)=0 and final angular velocity must be absent ω(T)=0 (these cases occur very frequently, especially if attitude control is done relative to inertial coordinate system). It is obvious, in moments of time t=0 and t=T, angular velocity calculated according to the formula (19), corresponding to nominal rotation (when E_k= 1/(2k₀)), is not equal to zero. Therefore, segments of acceleration and braking at the beginning and the ending of turn maneuver are inevitable. But segment of special control regime can be absent. Presence of this regime is determined by the values of Λ_in , ${\Lambda }_{\text{f}}$ for known J₁ , J₂ , J₃ . The most important characteristic is the integral

$S={\displaystyle \underset{0}{\overset{T}{\int }}\sqrt{J_1{\omega }_1^2+J_2{\omega }_2^2+J_3{\omega }_3^2}dt}$   (21)

which we name path functional, and it is minimum for motion according to the law (11), (13)²² (the integral S depends exclusively on the values of Λ_in , Λ_f and the moments of inertia J₁ , J₂ , J₃). The value S specifies type of optimal control and number of switching points for concrete values of J₁ , J₂ , J₃ , Λ_in and Λ_f).

Let L_max be the maximum value of the angular momentum modulus within the control interval [ 0 , T ]; L_nom is the module of the angular momentum in the interval of time with a special control regime (between acceleration and braking); L_imp and T_imp are the modulus of the angular momentum and the optimal time under impulse control (when the angular momentum at times t=0 and t=T changes abruptly from çL½= 0 to çL½= L_nom and from çL½= L_nom to çL½= 0, respectively). If special control regime is present during the optimal turn then the following equations must be satisfied:

t₁ = $\sqrt{1/k_0}/u_0$ , t₂ L_nom = S/C , t₁ < t₂ , t₁ + t₂ = Т, where L_nom = m₀ t₁ =$\sqrt{1/k_0}/C$

From this system of equations we obtain t₂ = $S\sqrt{k_0}$ = T_imp. From the requirement t₁ < t₂ we find the condition for the existence of a special control regime: k₀u₀S > 1. Thus, taking into account the prominence value of integral (21) we arrive at the following conclusion:

(а) if k₀u₀S > 1, then the optimal value is $r_0=2{\sqrt{K}}_0/C$ , and maximal energy is E_max = 1/(2k₀) (see (20)), relay control with two switching points is optimum;

(b) if k₀u₀S £ 1, then ❘M❘= const > 0, the special control regime is absent, and t₁ = $\sqrt{S/u_0}$ ; the function b (t) has a derivative $\dot{b}$ ≠0, the constant r₀ satisfies the condition $r_0\ge 2\sqrt{k_0}/C$ , and the optimal value of r₀ is r₀ =   $(k_0\sqrt{u_{0}S}+\sqrt{u_0/S}/u_0)/C$ ; maximal energy is $E_{\max }=u_0^2{t}_1^2/2$ ≤1/(2k₀); relay control with one switching points is optimum.

Essentially, the requirement of optimality (minimization of index (6)) is equivalent to restriction

$J_1{\omega }_1^2+J_2{\omega }_2^2+J_3{\omega }_3^2$  ≤ 2E_add =1 / k₀  (22)

where E_add is the maximum allowable energy of spacecraft rotation.

For the optimal turn (regardless of the presence or absence of a special control regime) t₁ ≤ t₂ , t₁ + t₂ = Т, t₂ L_max= S/C, L_max= m₀t₁ , and therefore t₁ ≤ $\sqrt{S/u_0}$  always. If a segment with a special control regime occurs, then t ₂=T_imp= $S\sqrt{k_0}$ , and L_max=L_nom=L_imp= $\sqrt{1/k_0}/C$ ; braking duration τ= t₁, since at the stages of acceleration and braking ❘M❘= m₀ and М$\left|\right|$ L. If k₀u₀ S ≤ 1, then there is no segment with a special control regime and t₂=t₁= $\sqrt{S/u_0}$ , L_max= $\sqrt{u_{0}s}/C$ . Regardless of u₀ , we have b_max≤L_imp , so E_max≤1/(2k₀), and if u₀ ≥u_кр , then b_max=L_imp and Т_opt=T_imp+L_imp /m₀ , and if u₀ < u_кр , then b_max < L_imp and Т_opt=Т_fast ; the critical value of u_кр is u_кр=1/(k₀S ). If u₀ = u_кр, then Т_opt=2T_imp, G= $8S\sqrt{k_0}/3$ , and the relative loss in optimality (the growth of the functional (6)) is δG=G/G_imp‑ 1=1/ 3.

If time of reaching the calculated angular velocity which is equal

${\omega }_{i\text{ nom}}=\frac{1}{J_{i}C\sqrt{k_0}}{p}_{i0}$

and duration of suppressing the angular velocity to zero are infinitesimal, then duration of reorientation is T=$S\sqrt{k_0}$ because modulus of angular momentum during uncontrolled motion (between acceleration and braking) is |L|= ${(C\sqrt{k_0})}^{-1}$ , where the integral (21) is calculated by the formula

$S=t_{\text{pr}}\sqrt{J_1^{}{\omega }_{1\text{cal}}^{\text{2}}+J_2^{}{\omega }_{2\text{cal}}^{\text{2}}+J_3^{}{\omega }_{3\text{cal}}^{\text{2}}}$

where t_pr is the predicted time of achieving the condition $\Lambda (t_{\text{pr}})={\Lambda }_{\text{f}}$ during free rotation from the position $\Lambda (0)={\Lambda }_{\text{in}}$ with initial angular velocity ω(0)= ${\omega }_{\text{cal}}$ ≠ 0 (according to the equations (1), (2) in which all values M_i=0). Note, the value S and the vector p₀, which satisfy optimal motion, are computed together. Remind

$C=\sqrt{p_{10}^2/J_1+p_{20}^2/J_2+p_{30}^2/J_3}$

For a spherically symmetric spacecraft and for a dynamically symmetric spacecraft, key characteristics and the constants of control law are determined straightforwardly, without integration of motion equations (1), (2). For a spherically symmetric spacecraft, the integral S is calculated as

$S=2J_1\arccos {\nu }_{\text{0}}$

Accordingly, optimal modulus of angular momentum during uncontrolled rotation is

$L_{\text{opt}}=2J_1\arccos {\nu }_{\text{0}}/T$

and kinetic energy is

$E_k=2J_1{\arccos }^2{\nu }_{\text{0}}/T^2$

For an axially symmetric spacecraft (when J₂=J₃), the integral S is equal

$S=J_2\beta$

optimal modulus of angular momentum during uncontrolled rotation is

and kinetic energy is

$E_k=J_2^2{\beta }^2({\cos }^2\vartheta /J_1+{\sin }^2\vartheta /J_2)/(2T^2)$

The optimal controls M_i and angular velocities w_i change according to the following laws:

M_i=0.5m₀ [sign (t₁ –t) + sign (t₂– t)]p_i   (23)

J_iw_i=0.5m₀ (T-çt–t₁½–çt–t₂½)p_i  (24)

where $t_1=\sqrt{\min (1/k_0,u_{0}S)}/u_0$ ; t₂=max( $S\sqrt{k_0}$ ,$\sqrt{S/u_0}$ ); Т=t₁+t₂ ; t₁ is moment of acceleration ending; t₂ is moment of the beginning of braking. If t₂>t₁ (i.e. when k₀>1/(u₀S), then we have control with two points of switching when phase of rotation with M=0 (between acceleration and braking) is not absent, t₀=t₁ also. If t₁=t₂ (i.e. when k₀≤1/(u₀S), then moments of time when M=0, are absent, we have control with one switching (braking follows acceleration at once). In section 3, we demonstrated earlier that kinetic energy E_k= 1 /(2k₀) if =0. It is obvious, E_k< 1 /(2k₀) at acceleration and braking. Hence, E_k≤ 1 /(2k₀) during the entire interval of time [0, T] (if u₀< 1/(k₀S), then E_max=u₀S/2< 1 /(2k₀) also). Thus, for optimal control (in sense (6)), the property E_max≤ 1 /(2k₀) is satisfied always.

Key properties and features of optimal solution

We can show that the found control (12), (13) is indeed optimum (since the functions and w_i calculated by formulas (12), (13) are single solution of the system (1), (9), (10), (11) if ω(0)= ω (Т)=0 and r_i=r₀p_i). For zero boundary conditions ω (0)= ω (Т)=0, in general case, slew maneuver includes two phases during which magnitude of the torque М is maximal possible: acceleration and braking, and phase of uncontrolled motion at which equations (20) are satisfied. This type of control is called as control with two points of switching (t₁ is moment of time when kinetic energy E_k achieves level k₀/2, and t₂ is moment of beginning of braking). A detailed analysis of the main reorientation stages: speedup, braking, and uncontrolled spacecraft rotation with the constant kinetic energy and angular momentum (relative to inertial coordinate system), shows that all three stages have a common property, namely, spacecraft rotates along the “trajectory of free motion”. It is characteristic for the “trajectory of free motion” that the direction of spacecraft’s angular momentum remains constant in inertial coordinate system. Taking into account that during the entire reorientation (on the entire time interval [0, T]) the torque M is parallel to the angular momentum vector L (i.e., the controlling moment acts in the same direction as L, or in the opposite direction, or equals zero), we can conclude that M×L=0, and, therefore, there are no reasons for a rotation of the angular momentum L in inertial coordinate system. Also, the integral (21) does not depend on the character of variation of the function |L(t)|,²² and S is equal to the value (21) for ideal mode (for motion according to (11), (17), (20)). However, there are such situations (under certain values S, u₀ , k₀) when the stage of uncontrolled motion is absent and M¹0 within the entire interval of control 0≤t≤T (braking replaces acceleration at once). This type of control is named control with one switching.

If $k_0{u}_0{S}_{ }{>}_{ }1$ , then t₂>t₁ (t₂≠t₁), optimal motion includes regime of special control; time of optimal reorientation is $T=S\sqrt{k_0}+1/(u_0\sqrt{k_0})$ ; $\dot{a}\left(T/2\right)=const=0$

If k₀u₀S =1, then t₂=t₁, time of optimal reorientation is $T=2/(u_0\sqrt{k_0})$ ; the derivative $\dot{a}$ (T/2)=0 but $\ddot{a}$ (T/2)=0.

If k₀u₀S ≤ 1, then we have control with one switching when maximal energy of rotation E_max< 1 /(2k₀), and duration of optimal reorientation is T=2 $\sqrt{S/u_0}$ ; point of switching is t₀= $\sqrt{S/u_0}$ , maximal energy of rotation is E_max=u₀S/2, maximal modulus of angular momentum is $L_{max} =\sqrt{u_{0}S}/C$ , therefore, the derivative $\dot{a}$ (T/2)<0 ( $\dot{a}$ <0 on the entire interval of time 0≤t≤T).

For spacecraft reorientation with limited control (by restriction (3)), key property of optimal motion remains valid is independent of number of switching, the proportion E_k/|L|² between the kinetic energy E_k and angular momentum L is constant on the entire interval of time 0≤t≤T, independently of duration of acceleration and braking (independently of presence or absence of the uncontrolled stage with M=0). Angular momentum L and rotation energy E_k are continuous functions of time. Therefore, the proportion ρ=E_k/|L|² is continuous function. For acceleration (or braking), the equalities (14) (or (16)) and |M|=const are satisfied. Therefore, the proportion ρ is constant within acceleration and braking. Between acceleration and braking, the equations (20) are satisfied; as result, ρ=const during free rotation. Hence, the proportion ρ=E_k/|L|²=const within time interval [0, T] because of a continuity of functionr. As consequence, modulus of torque M is identical for acceleration and braking, and it is equal to same magnitude

$m_0=u_0/\sqrt{2\rho }$ =u₀ /C

Angular momentum L does not change the direction relative to inertial coordinate system during acceleration, braking and at rotation between acceleration and braking (when spacecraft rotates by inertia), so, a direction of angular momentum in inertial coordinate system invariably on the entire interval of time [0, T]. Hence, in the presence of restriction (3), the equations (11) and (13) are satisfied at the entire interval of rotation from t=0 to t=Т. At acceleration and braking |М|=const=m₀, where m₀ > 0 is maximal admissible magnitude of the torque М in direction of angular momentum L. Since on entire interval of control J_i /|L|=p_i , the value m₀ is identical during both phases of acceleration and braking, and it is equal u₀ /C, where C is the earlier introduced constant which is unambiguously specified by the vector p₀ and moments of inertia J₁, J₂ , J₃. The condition |M|≤m₀ is satisfied within the entire interval of control, where m₀=u₀/C. Optimal torque M is parallel to motionless line relative to inertial coordinate system. Direction of this motionless line is determined by direction of the vector p (since the directions of angular momentum L and the vector p coincide). Hence, M=m(t)p. The scalar function m(t) is specified as m(t)=(M₁L₁+M₂L₂+M₃L₃)/|L| or m(t)=M₁p₁+M₂p₂+M₃p₃. Control function m(t) is three-positional relay or two-positional relay if optimum is control with one switching. The function m(t) can be written in the following form: m(t)=m₀ if |L|<L_opt and t<T/2; m(t)= –m₀ if $t\ge T-\tau$ ; m(t)=0 if $\tau \le t<T-\tau$ (it is obvious that situation m(t)=0 is absent if τ=T/2, because the condition $\tau \le t<T-\tau$ is not satisfied). Here, $L_{\text{opt}}=m_0\tau$ , and L_opt is modulus of angular momentum at moment of time t=T/2 (or during free rotation if phase of uncontrolled motion takes place); τ is duration of acceleration (braking). Note the spacecraft’s angular momentum satisfies the inequality |L|≤L_opt for any time t. If optimal control program has two points of switching L_opt= $1/(C\sqrt{k_0})$ ; if optimum is control with one switching L_opt= $\sqrt{u_{0}S/C}$ . For optimal control, spacecraft acceleration continues until angular momentum equals the target level

$L_{\text{tag}}=L_{\text{opt}}\circ \tilde{\Lambda }\circ {\Lambda }_{\text{in}}\circ p(0)\circ {\tilde{\Lambda }}_{\text{in}}\circ \Lambda$

Thus, it is proven the following conclusion: spacecraft’s reorientation occurs with the minimal value of the index (6) if and only if the spacecraft rotates according to the law (11), (23), (24). If allow a step like change of the angular velocity vector , then the proposed optimal control problem (the kinematic reorientation problem) can be considered solved: equations (2), (11), and (19) completely define the necessary motion (t), the main moment of forces is zero (i.e., the spacecraft’s rotation is an Euler–Poinsot motion of rigid body) within interval 0<t<T in which E_k=1 /(2k₀).

Topicality of the solved problem consists in the fact that by minimizing functional (6) the energy spent to perform spacecraft reorientation from position ${\Lambda }_{\text{in}}$ into position ${\Lambda }_{\text{f}}$ is bounded and maneuver time T is minimum. Narrow-mindedness of rotation energy was proven earlier (in section 4). If u₀→∞, then the value of integral (6) is G=2T, consequently, the time of the optimal turn is T=G/2, and, minimizing integral (6), we obtain the turn of the spacecraft for the minimum time. If the moment M is limited, some non-zero time is required for imparting the required angular momentum to the spacecraft and for suppressing the existing angular momentum to zero. A restriction on the magnitude of feasible controlling moment leads to the appearance of intervals with non-zero duration when spacecraft increases and decreases its angular velocity. Duration of optimal maneuver is

$T=S\sqrt{k_0}+1/(u_0\sqrt{k_0})$   (25)

if the special control regime is present (when k₀u₀S > 1). The first term is duration of so-called kinematic control (or ideal maneuver) when u₀→∞, t₁→0, and the equalities (17), (20) are satisfied within entire interval of time 0<t<T. This duration is minimal since S is minimal possible value since optimal maneuver (in sense (6)) satisfies equations (11), (13). Second term is duration of braking under restriction (3) (when u₀<¥ and u₀¹0). This time is minimal for control (16).²³ Hence, the value (25) is minimal possible value of reorientation's time with restriction (3) and condition E_k≤ 1 /(2k₀) for kinetic energy E_k during spacecraft maneuver. If optimum is control with one switching (because k₀u₀S ≤ 1), then energy E_k do not achieve the level E_add=1/(2k₀) under time-optimal control.¹³ Optimization in accordance with criterion (6) minimizes the time of spacecraft’s rotation from the position Λ(0)=L_in to the position Λ(T)=Λ_f in the presence of restrictions (3) and (22).

If $1/(u_0\sqrt{k_0})$  is much less than $S\sqrt{k_0}$ , the beginning of braking will be determined from the fact that the angular momentum magnitude |L(t)| changes linearly when angular velocity is reduced to zero. During braking, the modulus of the controlling moment is constant, and the time moment from which braking will be started is specified by the following condition:

$4\text{arcsin}\frac{K\sqrt{{\delta }_2^2+{\delta }_3^2}}{\sqrt{{(J_2{\omega }_2)}^2+{(J_3{\omega }_3)}^2}}=\frac{K^2\sqrt{{\omega }_2^2+{\omega }_3^2}}{m_0\sqrt{{(J_2{\omega }_2)}^2+{(J_3{\omega }_3)}^2}}$

where m₀ is the maximal controlling moment magnitude that can be provided by the actuators of attitude control system; δ_j are the components of the discrepancy quaternion $\tilde{\Lambda }(t)\circ {\Lambda }_{\text{f}}$ ; К=|L(t)| is the current magnitude of the angular momentum. The said condition for finding the start moment of braking phase allows the onboard control system to form a signal of angular velocity reduction based on the information on current spacecraft orientation and measurements of angular velocity. Use of this condition increases the precision of the spacecraft reorientation into final position Λ_f .

Construction of optimal control in specific cases

We assume that the control non-limited by any restrictions is ideal mode (in this case, u₀→∞ and t₁→0, the braking is momentary process also). For the optimal motion, spacecraft reorientation from one angular position ${\Lambda }_{\text{in}}$ to another position ${\Lambda }_{\text{f}}$ is done by impulsive imparting the necessary angular velocity (the nominal value of the angular momentum vector) to the spacecraft, rotation of the spacecraft with the constant kinetic energy and modulus of angular momentum, and short-term (impulse) reduction of the rotation energy to zero. In ideal motion optimal with respect to criterion (6), the spacecraft’s reorientation between impulsive acceleration and impulsive braking is carried out with zero controlling moment M=0. Constructing the optimal reorientation regime with minimal value of functional (6) is non-trivial task. In the optimal reorientation problem (in constructing the optimal programmed motion ω(t)), it is crucial to find the initial vector ω(0) and the corresponding angular velocity ω(0+) (the angular velocity (0+) is calculated by formulas (19)). The vector p(0) depends on reorientation parameters ${\Lambda }_{\text{t}}={\tilde{\Lambda }}_{\text{in}}\circ {\Lambda }_{\text{f}}$ and the spacecraft characteristics J₁, J₂, J₃. For arbitrary values J₁ ≠ J₂ ≠ J₃, it is hard to find the solution of the considered problem of spacecraft’s three-dimensional reorientation for arbitrary values ${\Lambda }_{\text{in}}$ and ${\Lambda }_{\text{f}}$ . The difficulty is to find the vectors p(0) and p(T) which are related by (18). Analytical solution of the system of equations (2), (11), and (19) exists for dynamically spherical and dynamically symmetric bodies only. For a spherically symmetric spacecraft (when J₁=J₂=J₃), the solution p(t), ω(t) have elementary form: p(t)=const and ω(t)=const, or in detail

$p_i={\nu }_i/\sqrt{{\nu }_1+{\nu }_2+{\nu }_3}$ , and ${\omega }_i=\frac{2{\nu }_i{\arccos }_{}{\nu }_0}{T\sqrt{{\nu }_1+{\nu }_2+{\nu }_3}}$

where ${\nu }_0,{\nu }_1,{\nu }_2,{\nu }_3$ are components of the reorientation quaternion ${\Lambda }_{\text{t}}={\tilde{\Lambda }}_{\text{in}}\circ {\Lambda }_{\text{f}}$ .

For a dynamically symmetric spacecraft (for example, when J₂=J₃), the optimal control problem can be solved completely also. For this distribution of spacecraft’s mass, the following differential equations

$J_2{\dot{\omega }}_2=\left(J_3-J_1\right){\omega }_1{\omega }_3$ , $J_3{\dot{\omega }}_3=\left(J_1-J_2\right){\omega }_1{\omega }_2$

are satisfied under condition . Last system of differential equations describes the oscillator (with the parameter ${\omega }_1=\text{const}$ ), for which ${\omega }_2$ and ${\omega }_3$ are harmonic functions of time. Therefore, р₁=const=р₁₀ and harmonic oscillations of the functions р₂ and р₃ are observed. In this special case, the optimal motion is the simultaneous rotation of the spacecraft as a rigid body around its axial axis OX and around spacecraft’s angular momentum L which is constant in the inertial space and which constitutes a certain constant angle with the spacecraft’s axial axis. Angular velocities with respect to OX and p axises have a constant ratio (as is shown above, the vectors L and p are parallel). The solution of system (2), (11), (19), necessary for solving the control problem, is regular precession. For the regular precession case

${\Lambda }_{\text{f}}={\Lambda }_{\text{in}}\circ {е}^{p_{\text{o}}\beta /2}\circ e^{e_{\text{1}}\alpha /2}$

where p₀=p(0); e₁ is the unit vector of the spacecraft’s axial axis; α is the spacecraft’s rotation angle around its axial axis; β is the spacecraft’s rotation angle around the vector p, e is the quaternion exponential.¹ It is assumed that |α|≤ π, 0≤β≤ π. For a spacecraft with moments of inertia $J_1\ne J_2=J_3$ , the solution p(t) is written as follows:

$\begin{array}{l}{p}_1=p_{10}=\text{const}=\cos \vartheta ,p_2=p_{20}\cos \kappa +p_{30}\sin \kappa \\ p_3=-p_{20}\sin \kappa +p_{30}\cos \kappa ,\kappa =\frac{J_3-J_1}{J_2}{\displaystyle \underset{0}{\overset{t}{\int }}{\omega }_1(t)dt}\end{array}$   (26)

In this case, dependences (26), together with equalities (19), form a solution of the system of equations (2), (11) under condition (13). At the same time, the vector p also generates a cone around the axial axis OX in the spacecraft’s coordinate system. The specific value of р₀ is determined exclusively by the requirement that, according to equations (2), (11), (19), boundary conditions (4) and (5) must be satisfied. In this type of control, the spacecraft’s angular momentum preserves a constant direction in the inertial reference basis I, while the axially symmetric body moves along a “conic trajectory”. To move the spacecraft from position ${\Lambda }_{\text{in}}$ into position ${\Lambda }_{\text{f}}$ , it rotates simultaneously around the vector c_E, which is constant relative to the inertial basis I, by the angle β, and around its own longitudinal axis by the angle α. Using the mathematical formalism of quaternions to describe rotations of rigid body about the center of mass, relations reflecting a dependence between the values p₀, α, and β are written. The dependence of parameters p₀, α, and β on the boundary angular positions ${\Lambda }_{\text{in}}$ and ${\Lambda }_{\text{f}}$ is given by the following system of equations:

$\begin{array}{l}\cos \frac{\beta }{2}\cos \frac{\alpha }{2}-p_{10}\sin \frac{\beta }{2}\sin \frac{\alpha }{2}={\nu }_0,p_{20}\sin \frac{\beta }{2}\cos \frac{\alpha }{2}+p_{30}\sin \frac{\beta }{2}\sin \frac{\alpha }{2}={\nu }_2,\\ \cos \frac{\beta }{2}\sin \frac{\alpha }{2}+p_{10}\sin \frac{\beta }{2}\cos \frac{\alpha }{2}={\nu }_1,-{р}_{20}\sin \frac{\beta }{2}\cos \frac{\alpha }{2}+p_{30}\sin \frac{\beta }{2}\cos \frac{\alpha }{2}={\nu }_3,\\ \alpha =\frac{J_2-J_1}{J_1}{p}_{10}\beta \end{array}$

For a known reorientation time T, angular rotation velocities around the OX and p axises are equal to $\dot{\alpha }=\alpha /T$ , and $\dot{\beta }=\beta /T$ (for ideal mode $T=S\sqrt{k_0}$ ). The magnitude of angular momentum during optimal rotation is |L|=J₂ β/T. The programmed values of controllable functions ω_i (projections of the angular velocity vector ω) have the following form:

${\omega }_1=\dot{\alpha }+\dot{\beta }{p}_{10},{\omega }_2=\dot{\beta }\sqrt{1-p_{10}^2}\sin (\dot{\alpha }t+{\sigma }_0),{\omega }_3=\dot{\beta }\sqrt{1-p_{10}^2}\cos (\dot{\alpha }t+{\sigma }_0)$

where ${\sigma }_0={\text{arctg}}_{}(p_{20}/p_{30})$ . Optimal values p₀, α, and β corresponding to solution of last system of five transcendent equations and which correspond to free motion from position Λ_in into position Λ_f can be determined with using the device.²⁹

For an asymmetric spacecraft (when J₁ ≠ J₂ ≠ J₃), the system (2), (11), (19) can be solved by numerical methods only (e.g., using the method of successive approximations or iterations methods with consecutive approach to true solution). To find the vector p₀, it is necessary the solving the boundary problem $\Lambda (0)={\Lambda }_{\text{in}}$ , $\Lambda (T)={\Lambda }_{\text{f}}$ , taking into account the equations (1), (2) imposed upon the motion, in which M_i=0. As a result, the value of the angular velocity vector at the initial time moment ${\omega }_{\text{cal}}$ , for which the spacecraft is moved by its free rotation with respect to the center of mass (M=0) from the state $\Lambda (0)={\Lambda }_{\text{in}}$ , ω(0)=${\omega }_{\text{cal}}$ into the state Λ(T)= ${\Lambda }_{\text{f}}$ , will be found (ω(T) is arbitrary here). In particular, the method of solving the boundary problem and determining the vector p₀ was described in detail in the article.¹³ The value of vector p₀ relates to ${\omega }_{\text{cal}}$ as

$p_{i0}=\frac{J_i{\omega }_{i\text{cal}}}{\sqrt{{\left(J_1{\omega }_{1\text{cal}}\right)}^2+{\left(J_2{\omega }_{2\text{cal}}\right)}^2+{\left(J_3{\omega }_{3\text{cal}}\right)}^2}}$

The known algorithms presented in patent²⁴ and system²⁵ can be used for finding calculated values ${\omega }_{\text{cal}}$ and p₀ also. These algorithms^13,24,25 are reliable and provide asymptotic approaching for sought value p₀. Other calculation schemes^30,31 can be useful only in some specific cases.

Thus, key results are the following: optimal control program of spacecraft reorientation was found; it was demonstrated that two-impulse control when spacecraft rotates by inertia between acceleration and braking is optimum in general case. Key characteristic properties of the obtained optimal motion are determined. All conclusions are absolutely true since well-known mathematical methods were used, and all mathematical formulas are based on the checked theories. For a dynamic symmetric spacecraft, a complete solution of the reorientation problem in closed form is presented; optimal values of control law parameters can be found by the device.²⁹ The obtained control method is differs from all other known solutions. Main difference consists in new form of minimized functional which allows to turn a spacecraft with the bounded rotation energy (maneuver time is minimized also). This useful quality is advantage of presented control mode because it significantly saves the controlling resources and increases the possibilities of spacecraft control. Furthermore, rotation with energy not exceeding the given value allows us to stop rotation of a spacecraft within known time what is very important in safety sense in critical situations.

Example and results of mathematical simulation

Spacecraft reorientation with minimal functional (6) is performed along the “trajectory of free motion”, on which the direction of the spacecraft’s angular momentum remains constant in inertial coordinate system on the entire time interval from t=0 to t=T. Optimal torque M is collinear to the vector p which is unit vector of angular momentum L. For cases when $\tau <<T$ , the strategy “acceleration of rotation, uncontrolled rotation, damping of rotation” is optimum for optimal control problem (1)-(6) if ω(0)=ω (T)=0 in slew maneuver. The assumed criterion of optimality supports motion of a spacecraft with the bounded kinetic energy of rotation during reorientation maneuver. The universality of the designed control method is proved by the following factors: it does not depend from actuators type, mass and size of spacecraft, spacecraft’s moments of inertia, altitude of working orbit (and from others, for example, from periodicity of reorientation, angle of a turn). Let us give a numerical example of solving the optimal control problem for spacecraft reorientation with minimal value of the integral (6). As an example, let us consider spacecraft reorientation for 180 degree from initial position ${\Lambda }_{\text{in}}$ , when body axes coincide with the axes of reference basis I, into the target position ${\Lambda }_{\text{f}}$ . It is assumed that initial and final angular velocities are zero, ω(0)= ω(T)=0. Values of the elements of quaternion ${\Lambda }_{\text{f}}$ that characterizes the target attitude of a spacecraft are:

λ₀=0, λ₁=0.707107, λ₂=0.5, λ₃=0.5

Let us find the optimal control program for angular velocity ω(t) for transferring the spacecraft from the state $\Lambda (0)={\Lambda }_{\text{in}}$ , ω(0)=0 to the state $\Lambda (T)={\Lambda }_{\text{f}}$ , ω(T)=0 if the coefficient k₀ is equal to k₀=0.5 joules^–1. The constant u₀ which characterizes power of actuators is u₀=0.05 N kg^–1/2. The spacecraft’s mass-inertial characteristics are as follows:

J₁=12801.6 kg m² , J₂=45747.3 kg m² , J₃=40331.1 kg m²

As a result of solving the turn boundary problem from position $\Lambda (0)={\Lambda }_{\text{in}}$ into position $\Lambda (T)={\Lambda }_{\text{f}}$ (the optimal reorientation problem in the impulse setting), we obtained the calculated value of the vector p₀= {0.4469347; -0.1861273; 0.8749891} and integral S=471.1 m $\sqrt{\text{kg}}$ . Iterations method guaranteeing successive approach to true value p₀ was used¹³ (in most cases, this method provides asymptotic approaching). The maximal value of the control torque is m₀=8.41 N m. The obtained value S shows that k₀u₀S > 1 and optimal program is control with phase of uncontrolled rotation. The durations of speedup and braking are the same and equal to τ=28.3 s, the angular momentum magnitude within stage of rotation by inertia equals L_opt=238 N m s. Optimal changing the controlling moment M is described by the law

М=u₀ [sign ($1/(u_0\sqrt{k_0})-t$ ) + sign ($S\sqrt{k_0}-t$ )] $\tilde{\Lambda }\circ$ Λ_in  p₀ $\circ {\tilde{\Lambda }}_{\text{in}}$ L / (2C)

Results of the mathematical modeling of the reorientation process under optimal control are given on Figures 1–3. Figure 1 shows the character of changing the angular velocities ω₁(t), ω₂(t), ω₃(t) with respect to time. The reorientation time is T=361.4 s. Between acceleration and braking, the spacecraft rotates with a constant energy equal to E_k=1 joules. The value of index (6), which characterizes the cost-efficiency of the rotation trajectory Λ(t), ω(t) after spacecraft’s angular motion from position ${\Lambda }_{\text{in}}$ into position ${\Lambda }_{\text{f}}$ , equal to G=685 s. Figure 2 shows the changes in the components of quaternion Λ(t) that defines current attitude of a spacecraft in process of rotation maneuver: λ₀(t), λ₁(t), λ₂(t), λ₃(t). Finally, Figure 3 shows the dynamics of the components p₁(t), p₂(t), p₃(t) of the unit vector p during optimal maneuver. The variables λ_j and p_i are dimensionless quantities. It is characteristic that the change in the projection p₁ is very small in comparison with changes in the projections p₂ and p₃ (the angular velocity component ω₁ also changes a lot less on the interval of free rotation than angular velocity components ω₂ and ω₃). This confirms the fact that the OX axis is longitudinal axis. Unlike variables ω_i, variables p_i and λ_j are smooth functions of time.

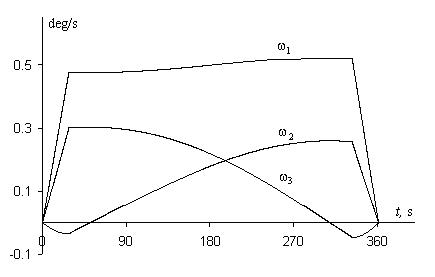
Figure 1 Changing the angular velocities during optimal reorientation maneuver.

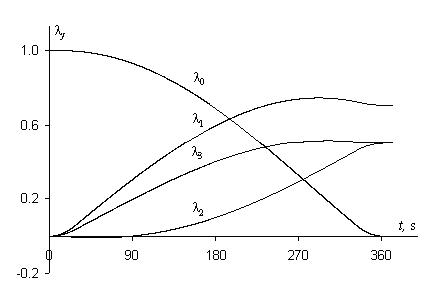
Figure 2 Changing the components of orientation quaternion Λ(t) during optimal reorientation.

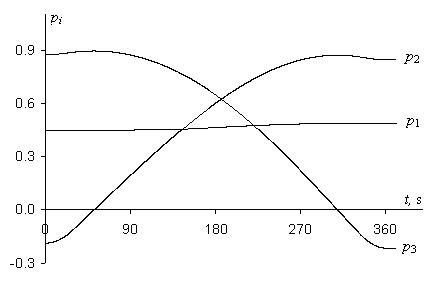
Figure 3 Changing the components of unit vector p under optimal control.

Control algorithm of angular motion is very significant element of control system of spacecraft attitude, booster units and orbital stations. Designing optimal algorithm of controlling a spacecraft motion increases efficiency of onboard control system of a spacecraft and originates more economical performance of spacecraft during flight on orbit. In this paper, the optimal control problem for spatial reorientation of a spacecraft from a position of rest to a position of rest is considered and solved. The optimization has been performed for case when rotation energy integral should be minimized together with turn duration. Finding the optimal mode of spacecraft reorientation with a minimal value of energy’s “expenditure” is quite topical. An analytic solution of the proposed problem is presented. Formal equations and computational expressions for constructing optimal reorientation program were obtained. To solve the formulated problem, the maximum principle is applied, and use of quaternions significantly simplifies computational procedures and reduces the computational costs of the control algorithm, which makes it suitable for onboard realization. Mathematical expressions, which provide for obtaining final equations and relations describing the variation of control functions and behavior of a spacecraft during optimal maneuver, is based on universal variables which were introduced earlier.² The main characteristic properties of optimal motion and the type of trajectory optimal with respect to the chosen criterion were determined. The reorientation problem has been solved completely in dynamic statement. Necessary optimality conditions were found, and the optimal control structure was determined; the formalized relations to determine the spacecraft’s optimal motion are obtained. The spacecraft reorientation control problem with regard to the constraints on the controlling torque is studied. For a specific form of these constraints, the problem of optimal reorientation was solved.

Minimization of the adopted index of quality is very important problem in practice of spacecraft flight, it limits rotary energy during maneuver, and therefore the spacecraft rotation can be damped for a time not exceeding the known value. The main results are the following: it was demonstrated that two-impulse control is optimum (with one or two switching), and, in many cases, spacecraft rotates by inertia between acceleration and braking. Ideal optimal solution is two-impulse control when spacecraft rotates by inertia between jump-like acceleration and jump-like braking. If the controlling torque is limited, analytical formulas were written for duration of acceleration and braking, and turn's time also. We have shown that direction of spacecraft’s angular momentum is constant in inertial coordinate system within the entire reorientation interval. Expressions for computing the temporal characteristics of the reorientation maneuver and the condition for finding the deceleration start moment based on factual kinematic motion parameters with use of terminal control principles are presented; it leads to high orientation precision. Example and results of mathematical modeling for spacecraft motion under optimal control are given. The obtained results demonstrate that the designed control method of spacecraft's three-dimensional reorientation is feasible in practice.

The made investigation concerns the theory of the controlled motion of a rigid body, and the obtained results are very important and can be used in practice of spacecraft flight, in particular. Importance of the proposed method of reorientation consists not only in energy aspects but in safety sense, since this rotation mode provides, at any time, a damping to zero angular velocity within a known duration non exceeding the given value (it is very topical in different critical situations). Presence of ready formulas, for synthesis of optimal motion program during a slew maneuver, does the carried out research as practically significant and suitable for direct use in practice of spaceflights.

None.

The author declares that there is no conflict of inertest.

None.

1. Branets, VN, Shmyglevskii, IP. Use of quaternions in problems of orientation of solid bodies, Nauka, Moscow, 1973.
2. Levskii MV. Use of universal variables in problems of optimal control concerning spacecrafts orientation. Mechatronics Automation Control. 2014;1:53–59.
3. Wells KC, Millet DB, Fuentes JD. Satellite isoprene retrievals constrain emissions and atmospheric oxidation. Nature. 2020;585(7824):225–233.
4. Parsons S. Planet discovered transiting a dead star. Nature. 2020;585(7825):354–355.
5. Kempton E. First exoplanet found around a sun-like star. Nature. 2019;575(7784):43–44.
6. Raushenbakh BV, Tokar EN. Spacecraft orientation control. Moscow: Nauka, 1974.
7. Alekseev KB, Malyavin AA, Shadyan AV. Extensive control of spacecraft orientation based on fuzzy logic. Flight. 2009;47–53.
8. Velishchanskii MA, Krishchenko AP, Tkachev SB. Synthesis of spacecraft reorientation algorithms using the concept of the inverse dynamic problem. Journal of Computer and System Sciences International. 2003;42(5):811–818.
9. Li F, Bainum PM. Numerical approach for solving rigid spacecraft minimum time attitude maneuvers. Journal of Guidance, Control, and Dynamics. 1990;13(1):38–45.
10. Scrivener S, Thompson R. Survey of time-optimal attitude maneuvers. Journal of Guidance, Control, and Dynamics. 1994;17(2):225–233.
11. Liu S, Singh T. Fuel/time optimal control of spacecraft maneuvers. Journal of Guidance, 1996;20(2):394–397.
12. Byers R, Vadali S. Quasi-closed-form solution to the time-optimal rigid spacecraft reorientation problem. Journal of Guidance, Control, and Dynamics. 1993;16(3):453–461.
13. Levskii MV. Pontryagin’s maximum principle in optimal control problems of orientation of a spacecraft. Control Systems for Moving Objects. 2008;47(6):974–986.
14. Shen H, Tsiotras P. Time-optimal control of axi-symmetric rigid spacecraft with two controls. Journal of Guidance, Control, and Dynamics. 1999;22(5):682–694.
15. Molodenkov AV, Sapunkov Ya G. A solution of the optimal turn problem of an axially symmetric spacecraft with bounded and pulse control under arbitrary boundary conditions. Journal of Computer and System Sciences International. 2007;46(2):310–323.
16. Molodenkov AV, Sapunkov Ya G. Special control regime in the problem of optimal turn of an axially symmetric spacecraft. Journal of Computer and System Sciences International, 2010;49(6).
17. Junkins JL, Turner JD. Optimal spacecraft rotational maneuvers. Elsevier, USA, 1986.
18. Kovtun VS, Mitrikas VV, Platonov VN, et al. Mathematical support for conducting experiments with attitude control of space astrophysical module Gamma. Technical Cybernetics. 1990;3:144–157.
19. Platonov VN, Kovtun VS. Method for spacecraft control using reactive actuators during execution of a programmed turn. Inventions. Applications and Patents. 1997.
20. Levskii MV. Features of attitude control of a spacecraft, equipped with inertial actuators. Mechatronics, Automation, Control. 2015;16(3):188–195.
21. Levskii MV. Special aspects in attitude control of a spacecraft, equipped with inertial actuators. Journal of Computer Science Applications and Information Technology. 2017;2(4):1–9.
22. Levskii MV. Optimal spacecraft terminal attitude control synthesis by the quaternion method. Mechanics of Solids. 2009;44(2):169–183.
23. Levskii MV. On optimal spacecraft damping. Journal of Computer and System Sciences International. 2011;50(1):144–157.
24. Levskii MV. Method of spacecraft turn control and the system for its realization. Inventions. Applications and Patents. 1998.
25. Levskii MV. Control system for spacecraft spatial turn. Inventions. Applications and Patents. 1994:49–50.
26. Zubov NE, Li MV, Mikrin EA, et al. Terminal synthesis of orbital orientation for a spacecraft. Journal of Computer and Systems Sciences International, 2017;56(4):154–173.
27. Pontryagin LS, Boltyanskii VG, Gamkrelidze RV, et al. The mathematical theory of optimal processes. Gordon and Breach, USA, 1986.
28. Young LC. Lectures on the calculus of variations and optimal control theory. EA: Saunders, USA, 1969.
29. Levskii MV. Device for regular rigid body precession parameters formation. Inventions. Applications and Patents. 2000.
30. Bertolazzi E, Biral F, Da Lio M. Symbolic-numeric efficient solution of optimal control problems for multibody systems. Journal of Computational and Applied Mathematics. 2006;185(2):404–421.
31. Kumar S, Kanwar V, Singh S. Modified efficient families of two and three-step predictor-corrector iterative methods for solving nonlinear equations. Journal of Applied Mathematics. 2010;1(3):153–158.