This paper deals with the global regulation problem for robot manipulators, a new logarithm-type control scheme is presented. The proposed control drives position error and derivative action terms plus gravity compensation. To ensure global asymptotic stability of closed-loop system equilibrium point, we propose an energy-shaping based Lyapunov function. Experimental results on a three-degree-of-freedom direct-drive robot manipulator are presented.

Today, robot manipulators are important tools in society, they carry out many tasks such as pick- and-place operations, paintings, circuit-board as- sembly, drilling, palletizing until space operations, physiotherapy, robotic operating rooms, and so on. These tasks require high-performance control algorithms with high performance.^1-3 The topic on control of robot manipulators (so-called regulation) is an area for research and with potential applications. It consists in to move freely in its workspace the manipulator end-effectors from any initial condition to a fixed de- sired position, which is assumed to be constant, regardless of its initial joint position.³ The proportional derivative (PD) and proportional integral derivative (PID) control algorithms are the most simplest regulators to achieve regulation of robot manipulators. We can cite several works using PID-Like control schemes and their versions with saturating structures, for example.^1-3

In this paper, we propose a new logarithm- type control scheme with gravity compensation for the global regulation problem of robot manipulators. The proposed control scheme is un- like other cited previously works; it is composed of logarithm functions, obtained by a suitable potential functions to drive both the position error and damping injection on the proportional and derivative terms, respectively. The proposed control scheme performance resulting is experimentally evaluated. This paper is organized as follows. Section 2 describes the dynamics of rigid robots. In Section 3, states the proposed control scheme and its global asymptotic stability proof is presented. Experimental results are analyzed in Section 4. Finally, conclusions are given in Section 5.

The dynamics of a serial n-link rigid robot with viscous friction and n degrees of freedom can be written as³

$\tau = M(q)\ddot{q}+C(q,\dot{q})\dot{q} +g(q)+B\dot{q}$ (1)

where $q,\dot{q},\ddot{q}\in {\text{IR}}^{\text{n}}$ are the position, velocity and acceleration joint vectors, respectively; $\tau \in {\text{IR}}^{\text{n}}$ is the vector of input torques, $M(q) \in {\text{IR}}^{\text{n}\times \text{n}}$ is the symmetric positive definite manipulator inertia matrix, $C(q,\dot{q}) \in {\text{IR}}^{\text{n}\times \text{n}}$ is the matrix of centripetal and Coriolis torques, $g(q) \in {\text{IR}}^{\text{n}}$ is the vector of gravitational torques obtained as the gradient of the robot potential energy due to gravity and $B\in {\text{IR}}^{\text{n}\times \text{n}}$ is the positive definite diagonal matrix for the viscous friction torques. The dynamics model has several fundamental properties which can be exploited to facilitate control system design (see³).

We define the position control problem. The problem of position control for robot manipulators consists of to propose a control scheme such that, the applied torque $\tau \in {\text{IR}}^{\text{n}}$ to robot joints $q(t)$ tend asymptotically to a constant desired joint position $q_d\in {\text{IR}}^{\text{n}}$ , regardless the initial conditions ${[q(0),\dot{q}(0)]}^T\in {\text{IR}}^{\text{2n}}$ , this is: $\underset{t\to \infty }{\lim }\left[\begin{array}{l}\stackrel{-}{q}\left(t\right)\\ \stackrel{.}{q(t})\end{array}\right]$ $\to 0\in {\text{IR}}^{\text{2n}},\forall t\ge 0,$ where $\tilde{q}\in {\text{IR}}^{\text{n}}$ is the joint position error, which is defined as $\tilde{q}=q_d-q(t)$ . To resolve the position control problem, we propose a control structure $\tau$ composed by a Logarithm function to drive both the position error and derivative action terms, plus a component of gravity compensation:

$\tau =k_p\left[In\left(\tilde{q}+\sqrt{1+{\tilde{q}}^2}\right)+\frac{2\tilde{q}}{{\left[1+{\tilde{q}}^2\right]}^2}\right]-K_v\left[\ln \left(\dot{q}+\sqrt{1+{\dot{q}}^2}\right)+\frac{2\dot{q}}{{\left[1+{\dot{q}}^2\right]}^2}\right]+g(q)$ (2)

Where $\tilde{q}$ is the $n\times 1$ vector of joint position error; $k_p,k_v\in {\text{IR}}^{\text{n}\times \text{n}}$ are positive definite diagonal matrices, which are called proportional and derivative gains, respectively. We use the notation $\left[In\left(\tilde{q}+\sqrt{1+{\tilde{q}}^2}\right)+\frac{2\tilde{q}}{{\left[1+{\tilde{q}}^2\right]}^2}\right]$ to represent the vector of the proportional term, this is, each component of this vector has the same mathematical structure. This is the same idea for the derivative term. The close-loop system equation is obtained by combining the robot dynamics model (1) and the control law (2) as follows:

$\frac{d}{dt}\left[\begin{array}{l}\tilde{q}\\ \tilde{q}\end{array}\right]=\left[\begin{array}{l}-\dot{q}\\ M{\left(q\right)}^{-1}[k_p\left(In(\tilde{q}+\sqrt{1+{\tilde{q}}^2}+\frac{2\tilde{q}}{{[1+{\tilde{q}}^2]}^2}\right)\\ -K_v(In(\dot{q}+\sqrt{1+{\dot{q}}^2})+\frac{2\dot{q}}{{[1+{\dot{q}}^2]}^2})-B\dot{q}-C(q,\dot{q})\dot{q}\end{array}\right]$ (3)

Which is an autonomous nonlinear differential equation, and the state origin ${\left[\tilde{q},\dot{q}\right]}^T=0\in {\text{IR}}^{\text{2n}}$ is the unique equilibrium point of the dynamics system (3).

Consider the robot dynamics model (1) together with the control structure (2), then equilibrium point ${\left[\tilde{q},\dot{q}\right]}^T=0\in {\text{IR}}^{\text{2n}}$ of the close-loop system (3) is globally asymptotically stable.

To carry out the stability analysis, we propose the following Lyapunov function candidate composed by the sum of the robot manipulator kinetic energy plus arti_cial potential energy:

$\begin{array}{l}v(\dot{q},\tilde{q})=\frac{1}{2}{\dot{q}}^{T}M(q)\dot{q}+{\left[\sqrt{\tilde{q}In(\tilde{q}+\sqrt{{\tilde{q}}^2+1})-\sqrt{{\tilde{q}}^2+1}-\frac{1}{1+{\tilde{q}}^2}+2}\right]}^T{k}_p\sqrt{\tilde{q}In\left(\tilde{q}+\sqrt{{\tilde{q}}^2+1}\right)-\sqrt{{\tilde{q}}^2+1}-\frac{1}{1+{\tilde{q}}^2}+2}\\ \end{array}$ (4)

The time derivative of the Lyapunov function candidate (4) along the trajectories of the closed loop equation (3) is given by:$\dot{v}(\dot{q},\tilde{q})=-{\dot{q}}^{T}B\dot{q}-{\dot{q}}^T{k}_v\left[In\left(\dot{q}+\sqrt{1+{\dot{q}}^2}\right)+\frac{2\dot{q}}{{[1+{\dot{q}}^2]}^2}\right]\le 0$

Now, we use LaSalle's invariance principle in the region $\Omega =\left\{\tilde{q}=0\in {\text{IR}}^{\text{n}}\Lambda \dot{q}=0\in {\text{IR}}^{\text{n}}:V(\tilde{q},\dot{q})=0\right\}$ , then it is concluded that origin of state space is globally asymptotically stable.

To support our theoretical developments, we use the three degrees-of-freedom direct-drive robot manipulator shown in Figure 1. The experimental results consist of moving the manipulator end-effectors from its initial position to a fixed desired target. The initial positions and velocities were set to zero (at home position). The gains $k_p=diag\left\{15.75,35.3,12.5\right\}Nm$ ,and $k_v=diag\left\{0.225k_{p1},0.14k_{p2},0.2k_{p3}\right\}Nm$ ; they were tuned to prevent saturation of the actuators, which deteriorate the control system performance and leads the thermal and mechanical problems. Several trials were necessary in order to ensure a fast response of transient state, no oscillations, a minimum overshoot and smaller steady-state error, and keep the actuators within their torque capabilities.

Figure 1 Experimental robot manipulator.

Figure 2 contains the experimental results of position errors corresponding to three joints for the control ln(). Observe that, each profile converges asymptotically to zero, after a smooth transient, all the components tend asymptotically to a small neighborhood of equilibrium point. The transient response of position errors not has oscillating, neither peak values nor overshoot; in addition the robot's response achieving stationary-state times shorter than 1.7 seconds. The position errors in steady-state have small values ${\left[{\tilde{q}}_1(t),{\tilde{q}}_2(t),{\tilde{q}}_3(t)\right]}^T={\left[1.40,0.37,1.77\right]}^T$ degrees; therefore its Euclidean norm for this time is $\Vert \tilde{q}(t)\Vert =2.2869$ degrees. The errors are present due to presence of static friction at the servomotors; however, they are acceptably small.

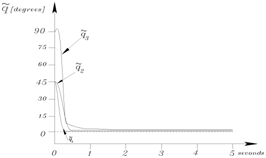
Figure 2 Experimental results of position errors.

In this paper, we have presented a new logarithm type control algorithm to solve the position control problem. The proposed control drives the position error to zero; this feature is due to its logarithmic structure. Our propose is supported by an asymptomatically stability analysis in sense Lyapunov's stability, and therefore, the global regulation objective is proved. The proposed control scheme permits the implementation of large number of hyperbolic-type control structures with potential applications at the industrial sector; and opening new control design possibilities to improve their closed-loop behavior.

None.

The author declares there are no conflicts of interest.

1.  Aguinaga E, Zavala A, Santibanez V, et al. Global Trajectory Tracking Through Static Feedback for Robot Manip- ulators with Bounded Inputs. IEEE Trans-actions on Control Systems Technology. 2009;17(4):934–944.
2. Caverly RJ, Zlotink DE, Bridgeman LJ, et al. Satu-rated Proportional Derivative Control of a Single-Link Flexible-Joint Manipulator. Transactions of the Canadian Society for Mechanical Engineering. 2014;38(2):658–666.
3. Siciliano B, Kathib O. Handbook of Robotics. 2nd edn. Springer; 2016.