This paper addresses the cooperative control with connectivity maintenance problem for multi-agent systems. It is assumed that each agent has the same sensing capability, that is to say, each agent can access the relative measurements from its neighboring agents constrained by its sensing maximum distance. In order to fulfill the control objective, the interaction topology of multi-agent systems is first modeled as the graph, and a feasible set of weights is given according to the actual distances of edges established in the graph. Then, a decentralized non-linear controller is provided, which guarantees the property of connectivity maintenance. Moreover, using the above obtained results, the stability analysis of cooperative control for multi-agent systems is investigated by the Lyapunov theory, which shows that the control objective is achieved. To demonstrate the effectiveness of the proposed control schemes, several numerical simulation results are presented.

Keywords: multi-agent systems, cooperative control, connectivity maintenance, laplacian matrix

Multi-agent systems have received a great deal of attention by many researchers from different subjects, which can provide a highly efficient way to perform some particular tasks in extreme environments. Many potential practical applications of Multi-agent systems can range from, for instance, space-based interferometers, surveillance, and reconnaissance systems, hazardous material handling, and distributed reconfigurable sensor networks. Hence, agents are required to cooperate to achieve these tasks, which means that agents must interact with each other, in general, each agent should receive some local information needed to accomplish the tasks, which implies that the objective is to present a control approach that meets several physical constraints.^1-3

It is assumed that agents can communicate with each other in terms of the sensing constraints, then necessary information can be obtained by using the wireless communication sensors, generally, such information can include states, relative measurements between any two agents and the distances in the Euclidean space.^4,5 It is also pointed that the information of each individual agent is always limited due to the presence of physical communication constraints. Therefore, the information interaction plays a critical important role in the cooperation (or coordination) control of multi-agent systems.^6,7 As a consequence, the resulting communication architecture of the agents can be abstracted by a graph, which is often called information graph. As a result, a dynamic proximity graph is developed, generally speaking, which relies on the information states of agents, the dynamic topology of the graph can be generated simultaneously according to the movements of agents, which results in different algebraic connectivity properties, therefore, it is meaningful to study the connectivity of the graph modeled by a team of agents. In practical application, for example, the soldiers should react to the potential threats in different terrains and battlefield situations while keeping in touch with each other.

The valuable information can be obtained by investigating the spectral properties of graph Laplacian, i.e., the eigenvalues and eigenvectors, thus the basic structure of graph can be clearly characterized, while the local and limited information can be obtained by each agent due to limited sensing ability and local communicate with other agents, and eigenvectors are easily computed, thus the decentralized control algorithm is considered.^8,9 In this paper, we will investigate the nature and performance of the network of agents by investigating its corresponding eigenvalues of the Laplacian L(G). In 1973, Fielder¹⁰ defined the algebraic connectivity as the second smallest eigenvalue λ₂(L) of Laplacian matrix for undirected graph. Specifically, the connected graph can be fully characterized by using the sign of λ₂(L). it is difficult to maintain the connectivity as the connectivity is a time-varying function of movement of the vertices.¹¹ To this purpose, several control strategies are proposed by applying the useful information from the relation between the connectivity and second smallest eigenvalue.^12,13 In general, using the information states of the system, mathematically, λ₂(L) can be represented. In addition, each agent has local information from its neighbors defined by proximity graph described as follows or R-disk graph,¹⁴ which implies that agent does not have the value of the quantity λ₂(L), or equivalently, in this way, λ₂(L) can hardly be computed directly, thus the optimization methods are used.^15,16 In particular, if any two agents have no interaction or the local information of one agent is not available to the other agent, then the relationship between them is not established, and the corresponding graph is not connected, thus we have λ₂(L)=0, and λ₂(L)=n if the graph is fully connected, namely, each agent have relationships with the rest of agents, from the information flow point of view, the shared information are regarded as the information states of all agents, such information is not easy to obtain in the real applications.

As indicated in,¹⁷ a theoretical framework is presented, and connectivity maintenance methods are discussed. In general, two main different approaches are developed to deal with connectivity maintenance problem in multi-agent systems networks, that is local and global connectivity based decentralized control. Decentralized approaches for controlling local connectivity in agent networks have been developed (see e.g.^18,19). As illustrated in,²⁰ the authors proposed a decentralized control method for maintaining the global connectivity in mobile robotic systems, both simulation and experiment results are provided to validate the effectiveness of the proposed algorithm.²¹ Using the bounded control inputs, the authors first proposed control algorithm for maintaining the global connectivity, and a theoretical analysis of the disturbance are presented as well. In order to achieve coordinate control tasks, keeping communication among agents and inter-agent sensing costs limited are major aspects of implementing coordinated tasks in multi-agent systems, which is needed to considered, where the cardinality of the directed edges |E| is defined as communication (or sensing) cost, which is usually defined as communication complexity.

In this paper, motivated by above discussion, we focus on maintaining the connectivity of the dynamic network for a team of agents and the consensus control is used to validate the proposed control approach. To accomplish our control objective, we suppose that each agent can only have local and limited information, which poses theoretical and practical challenges. We investigate the algebraic connectivity of graph by using the second smallest eigenvalue λ₂(L) defined by Fielder. The estimate of λ₂(L) can be usually computed by using power iteration method. Moreover, the dynamic edge weight is defined, which is usually referred to as edge (or called link) tension. In addition, a sufficient condition for a non-negative matrix is derived, which guarantees the eigenvalues are positive numbers. To maintain the connectivity of the graph, the energy function is defined and the stability of the system is analyzed later.

The remainder of the paper is organized as follows. Some basic terminologies of graph theory and problem formulation are given in Section II. A control strategy using local and limited information is proposed in Section III. Stability analysis of control law and convergence of consensus on information architecture for multiple agents are investigated in Section IV. Numerical simulation results are provided to illustrate the theoretical results in Section V. Finally, the conclusions are presented in Section VI.

In this section, we review some of the useful terminologies of graph theory used throughout in this paper. A graph G=(V, E) is composed of two sets of nodes (or vertices) V and links (or edges) E, respectively. We can label them with integers in numerical order, namely, {1, 2,…, n}, for future reference, thus the set of nodes V={v₁, v₂,…, v_n} is determined. Based on this, the edge set E = {e₁, e₂,…, e_n} can be recognized if there exists an edge e_k ∈ E between agent i and agent j for all (i, j) ∈ {1, 2,…, n}. In general, the number of edges is no less than the number of vertices, which is considered in the sequel. An ordered pair of nodes (i, j) is called if single direction is assigned to the edges, specifically, vertices i and j are the parent point and the childhood point, respectively, the important relation (i, j)=(j, i) is guaranteed, and vice versus, geometrically, which is usually denoted by a single arrow, notice that, called unordered pair, if it can be denoted by double arrow or simple line, i.e., (i, j)=(j, i)∈E.

An undirected graph is only considered in this paper, for simplicity, which is directly referred to as a graph. The directed graph is called if all the edges in the graph are ordered pairs of nodes, and the undirected graph are created if all the edges in the graph have the property of (i, j)=(j, i)∈E. A directed path is a sequence of edges satisfies that the vertices taken from the vertices set V are different in the path, self-loops and multiple edges are neglected, i.e., v₁ → v₂ → v₃ → v_k with v_k∈V, where v₁ and v_k are interpreted as the start node and the end node, respectively, and {v₂, v₃,…, v_k−1} the intermediate nodes. Note that the self-loop edge v_i → v_i consists of one vertex i such that both start vertex and end vertex are the same.^5,22 A directed graph is referred to as strongly connected if there exists a path generated by any two nodes (v_i → v_j), i= j, (i, j)={1, 2,…, n} with the specified direction of the edges. According to the above results, the information topology of the formation for multi-agent is abstracted to the corresponding graph, where each agent i is represented the vertex v_i, i.e., a_i → v_i.

To introduce the concept of algebraic connectivity, we first define a neighborhood set of agent i, which is widely used in the rest of this paper.

From a practical point of view, it would be interesting to consider the mobile networks, because the communication networks created by a group of agents are characterized by temporal variations and the real time movements of individual agents.^23,24 Jadbabaie et al.²⁵ studied the stability properties of coupled non-linear oscillator networks under the spectral graph theory and control theory; moreover, Poonawala and Spong⁵ investigated the strong connectivity problem in directed proximity graphs, the decentralized control strategy is proposed, despite the presence of disturbances or additional control objectives, the strong connectivity can be maintained.

[Neighborhood set]. For an agent i, we define the neighborhood set of agent i, denoted by N_i={j, (i, j)∈E} with respect to agent i, i.e., agent j is the neighbor of agent i, implying that agent i can acquire the relative information form N_i, such as relative positions, distances and angles in its local coordinate system, that is to say, the agent j∈ N_i can be view as attractive goals to agent i. Note that the total number of neighbors for agent i is the cardinality of neighborhood set, denoted by |N_i|.

From Figure1, three terminologies related to graphs are provided, namely, strongly connected graph, unilateral connected graph and weakly connected graph, respectively. For a graph G = (V, E), if there exists only a path Γ_u consists of vertices and edges, such that ∀ (v_i, v_j ) ∈ V and v_i ↔ v_j , i.e., v₁ → e₁ → v₂ → e₂ → v₃ → e₃ → v₄ → e₄ → v₁ , with the edge e_k=(v_i, v_j).

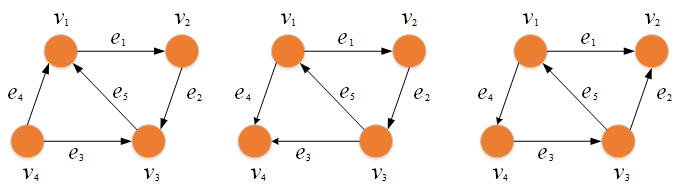
Figure 1 (A) Strongly connected graph; (B) Unilateral connected graph; (C) Weakly connected graph.

To proceed, we now introduce the important concept of the proximity graphs with the quantity △, where △ can be view as the feasible distance or maximum distance; hence the resulting proximity graphs are referred to as △-disk proximity graphs. Our purpose here is how to define the relative edge between agents i and j, to this end, the standard procedure is applied and its definition is then provided as follows.

[Proximity Graphs] Let p_i (x_i(t), y_i(t)) and p_j (x_j(t), y_j(t)) be the positions of agent i and j in 2-dimensional plane, respectively, d_ij the Euclidean distance, i.e.,

$d_{ij}=\sqrt{{\left(x_i\left(t\right)-x_j\left(t\right)\right)}^2+{\left(y_i\left(t\right)-y_j\left(t\right)\right)}^2}$ (1)

which results in dynamic proximity graphs characterized by the time-varying states p_i(t) and p_j(t). We here assume that d_ij=d_ji by neglecting model errors, such as the parameter sensor noise and sensor bias. For undirected proximity graph, for instance, if d_ij≤△, agent j has entered the measurable area of agent i, or equivalently, the information of agent j is available to agent i, and vice versus, as a result, the dynamic edge (or link) e_k is generated between two vertices v_i and v_j, and if agents are out of range of each other, namely, d_ij>△, no information about each other is acquired by agents i and j, thus no edge is established between two agents i and j. For brevity, we use l(e_k) to denote the edge relation as

$\mathcal{l}\left(e_k\right)=\{\begin{array}{cc}1,& d_{ij}\le \Delta ,\\ 0,& otherwise.\end{array}$ (2)

with above results in hand, a proximity graph is obtained, which can provide a rigorous formalization of interaction topology of multiagent system.

As indicated, according to the dynamic nature of the proximity graphs, one can readily observe that an edge should be appeared and disappeared simultaneously. In order to characterize the desired formation, information interaction plays a critical role to the topology of agents, suppose that each agent should interact with its neighbors to obtain necessary knowledge used to change its interior state by selecting appropriate controller. Using the definition of neighborhood set, we present the following assumptions.

As before, suppose that each agent has the same measure range, denoted by △, thus the sensing area of agent i is the sphere Ω_△ with radius △. When agent j∈ N_i travels into this area Ω_△ of agent i, the relative measurements are obtained by agent i, note that not all agents are within this area can be sensed by agent i, for instance, three agents are located at the same line. Moreover, the relative displacement between agent j and agent i can be obtained by agent j, this requirement is readily satisfied if we assume agent j can acquire knowledge from agent i by using the visual sensor.

To proceed, let m be the cardinality of edges, together with the total number of vertices n mentioned above, then the incidence matrix of the graphs, denoted by M(V, E)_n×m=[m_ij] are obtained, with each entry m_ij=1 if i is the start vertex of edge e_k, k={1, 2,…, n}, m_ij=−1 if i is the end vertex of edge e_k , k={1, 2,…, n}, otherwise, m_ij=0.

In view of M(V, E)_n×m , the Laplacian matrix L(V, E) is given as

$L\left(V,E\right)=M\left(V,E\right)M{\left(V,E\right)}^T\in R^{n\times n}$ (3)

Note that Laplacian matrix can also be defined by L(V, E)=D(V, E)−A(V, E) ∈ R^n×n , where D(V, E) and A(V, E) denote the diagonal matrix and adjacency matrix, respectively. We are now ready to state some important properties of Laplacian matrix L(V, E) below.

One can readily verify that i) L(V, E) is positive semi-definite and symmetric; ii) Each row sum of L(V, E) is equal to zero, the rest eigenvalues are positive numbers, i.e., {λ₂, λ₃,…, λ_n } > 0, moreover, we assume that λ₂<λ₃<,…, < λ_n , apparently, the total number of different positive eigenvalues is n–1; iii) The smallest eigenvalue of L(V, E) is always 0, whose corresponding eigenvector is typically, with 1_n is the column vector consisting of each component equals to one. In particular, we have Null (V, E)=span{1} when graph G is connected, where Null(V, E) represents the null space of G. In the case of undirected graphs G, we introduce the following well-known property:

${\lambda }_2\left(L\right)=\min \frac{P^{T}LP}{{\Vert P\Vert }^2}$ (4)

with superscript T representing the transpose, P taking from (10) defined in the section III.

We next introduce the important concept of algebraic connectivity. As mentioned above, for undirected graphs, the first positive eigenvalue λ₂ taken from eigenvalues {λ₂, λ₃,…, λn} of its associated Laplacian (3) is called the Fiedler eigenvalue, which is also defined as algebraic connectivity.

Let $X\in R^{n\times n}$ be an appropriate permutation matrix,$\Psi \in R^{n\times n}$ the upper block triangular, if $X^{-1}{M}_x\in \Psi$ , then M is referred to as the reducible matrix. If M is not reducible, then M is irreducible.

[Balanced Graphs]: If the total numbers of out-degree D_out (v_i ) and in-degree D_in (v_i ) of a vertex v_i are equal, namely, D_out (v_i)=D_in (v_i), then the vertex v_i of a directed graph G is balanced. Moreover, for all i, j∈V, iff all vertices of a directed graph G are balanced, then the directed graph G is called balanced, which is shown in Figure 2. Apparently, each node (v_i, i ∈{1, 2, …, n}) of a bi-directed graph is balanced, thus a bi-directed graph is balanced.

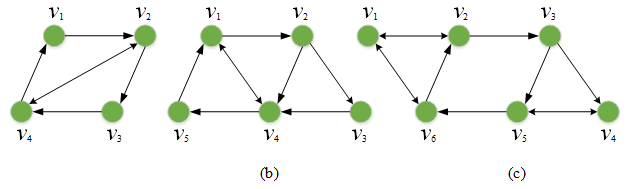
Figure 2 Three cases of balanced graphs.

Using (3), for a undirected graph G(V, E) , we can define a Lyapunov candidate function (or called Lapalacian potential) as

$V_G=\frac{1}{2}{\displaystyle \sum _{j\ne i,j\in N_i}^n{\alpha }_{ij}}\varphi (p_i,p_j)$ (5)

where ${\alpha }_{ij}$ is the entry of the adjacency matrix A(V, E), i.e., ${\alpha }_{ij}\in A(V,E)$ , to be specific, ${\alpha }_{ij}$ =1 if , otherwise, ${\alpha }_{ij}$ = 0. Physically, the agents i and j are within the △-proximity graphs as time evolves. Note that, if the edge e_k = (v_i, v_j)∈ E is established at a special time t= t₀, which will be contained in the networks of a group of agents i and j in future t>t₀. The undirected graph is called if  is a function that depends on both states p_i and p_j, the following properties should be satisfied.

1. $\Phi (p_i,p_j)$ is a continuous function, and $\Phi (p_i,p_j)<l$ , where l denotes a bounded constant number, i.e., $l<\infty \in R$ , since the feasible distance domain defined as above.
2. $\Phi (p_i,p_j)$ is a non-negative scalar function $\Phi (p_i,p_j)=0$ , if and only if $p_i=p_j$ , i.e., $p_i-p_j$ is the relative measurement between agents (or nodes) i and j.

To obtain the gradient flow of (5), we first introduce the gradient operator ${\Delta }_{pi}$ with respect to p_i, namely,

${\nabla }_{p_i}:=\frac{\partial }{\partial p_i},i\in \left\{1,2,\mathrm{...},n\right\}$ (6)

then the gradient flow of (5) is calculated as

${\dot{p}}_i=-{\nabla }_{p_i}{V}_G$ (7)

The (7) can be viewed as the control input or velocity of p_i, which needs to be determined, thus the controller is obtained by designing the control input, which is usually called as the gradient descent approach.

In order to find the value of algebraic connectivity λ₂(L) of the weighted Laplacian matrix, we define a matrix as

$H=I_n-\varsigma L_{n\times n}$ (8)

where I_n denotes the identity matrix; ς is a sufficiently small positive number. To this end, each entry $h_{i,j},i,j\in \{1,2,\mathrm{...},n\}$ of $H={\left[h_{i,j}\right]}_{n\times n}$ is a zero or positive number by selecting a proper value of ς, which is readily achieved, to be specific, for instance, we can choose $\varsigma \le \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.$ . With the help of H, the estimate of λ_i can be calculated. For this purpose, the basic procedures of power iteration method are briefly introduced as follows.

For a given matrix A, selecting the initial vector x⁽⁰⁾ randomly , the computing algorithm is given as

for i = 1, 2, …, n

$y^{\left(k+1\right)}=A{x}^{\left(k\right)}$

${\alpha }_k=max\left(y^{(k)}\right)$ ,

${\lambda }_1=max\left(y^0\right)/max\left(x^0\right)withmax\left(y(k)\right)={\left|\left|y^k\right|\right|}_{\infty }$ ;

$x^{(k+1)}={\alpha }_k{y}^{(k)}$ .

if $\left|m^{k+1}-m^k\right|<$ , where > 0 is sufficiently small number.

end

end.

Note that all eigenvalues and corresponding eigenvectors will be calculated. Moreover, we can readily verify that all eigen values λ_i (H) have following important property, namely, $\left|{\lambda }_i(H)\right|<=1$ , as the property of spectral norm of H. H=[h_ij] is the right stochastic matrix or transition matrix, each component h_ij is defined as

$h_{ij}=\{\begin{array}{cc}\varsigma ,& \left\{i,j\right\}\in E\\ 1-\varsigma d_i& i=j\\ 0,& otherwise\end{array}$ (9)

with d_i denoting the degree of vertex i. In order to guarantee the non-negative entry h_ij of H and the convergence of the system, the sufficient condition for ς can be deduced by $\varsigma \in (0,\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$d_{\max }$}\right.)$ with d_max representing the

maximum value of degree vector, i.e., $d_{\max }=\{d_1,d_2,\mathrm{..},d_n\}$ , which can be readily obtained if the maximum number of neighbors defined in the proximity graph is determined. Note that the system is unstable as the negative eigenvalue is computed if $\varsigma =d_{\max }$ . This case here is avoided.

In this section, we propose a distributed control strategy using the local measurements for multi-agent system. Consider a team of agents, as before, the positions of agents are given in the following form

$P={[p_1^T,p_2^T,\mathrm{...},p_n^T]}^T,i=\{1,2,\mathrm{...},n\}$ (10)

where $p_i={[x_i,y_i]}^T\in R^2$ is the position of agent i. As such, the configuration of the team of agents can be rewritten in compact form $P\in R^{2n}$ . In what follows, for notational simplicity, we use symbol p_i to denote the $p_i=(x_i,y_i)$ .

Suppose each individual agent is governed by a single-integrator, one obtains

$q_i=u_i,i=\{1,2,\mathrm{...},n\}$ (11)

where p_i remains the same as before, u_i denotes the control input that is needed to determined, which is also referred to as the velocity of agent i. To proceed, in light of the dynamic proximity, the useful notion is then presented as follow.

Let ${\omega }_{ij}$ be weights that assigned to the edges {i, j}, and ${\omega }_{ij}$ depends on the states i and j, mathematically, which can be expressed as

$\omega \text{ij = }\varphi {\text{(d}}_{\text{ij}}\text{)}$ (12)

where d_ij is the actual distance between agent i and agent j. Note that Equation (12) is a smooth function. Moreover ${\omega }_{ij}=\Delta$ ,if $d_{ij}>\Delta$ .

As indicated, in terms of ${\omega }_{ij}\in (0,\Delta )$ , the edge e_k (v_i,v_j) between agent i and agent j is established. More specifically, we define the edge-weights by using the bump function as

${\omega }_{ij}=\{\begin{array}{l}{e}^{-{(||p_i-p_j||-d_0)}^{\text{2}}/d_f}\\ 0\end{array}$ (13) 

where d_fs denotes the maximum sensing distance for each agent, to be specific, d_fs is equal to d_max, which will be discussed later.

It is evident that (13) is a smooth function, which implies that the (13) is a continuously differentiable and can be viewed as the variant of the Gaussian function, which is illustrated in Figure 3. Note that the quantity value of ${\omega }_{ij}$ takes on [0,1], i.e.,${\omega }_{ij}\in (0,1)$ and ${\omega }_{ij}={\omega }_{ji}$ because of $d_{ij}=d_{ji}$ , which can greatly simplify the computation complexity. It is also noted that ${\omega }_{ij}$ =0, i={1, 2, …, n}, by convention, the self-loops in the graph is precluded. Moreover, the degree of vertex i is defined by

$d_i={\displaystyle \sum _{j=1}^n{\omega }_{ij}},\{v_i,v_j\}\in E$ (14)

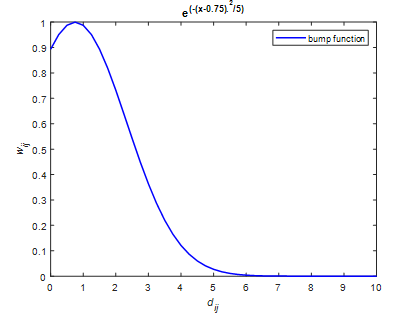
Figure 3 The edge weight ωij (or bump function) varies with the actual distances dij between any two agents

Since ${\omega }_{ij}$ denotes the actual relation between any two vertices i and j, which means that the dynamic properties of multi-agent system can be revealed by ${\omega }_{ij}$ , therefore, it is instructive to investigate the quantity ${\omega }_{ij}$ , moreover, the interaction topology of agents can be dynamically determined as well, it is noted that the agents i and j, i, j={1, 2, …, n} are assumed to interact positively. As a result, we consider a smooth function ${\omega }_{ij}$ that depends on the relative distance of agents i and j. To obtain this function, we will provide several important concepts as follows. In order to facilitate our analysis, the limited information obtained from a given valid sensing area of agent i is provided, which is shown in Figure 4.

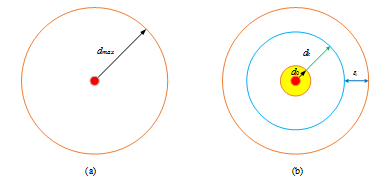
Figure 4 (A) The feasible sensing area of agent i; (B) Geometrical constraints. We use solid red point denote agent i, dmax denotes the maximum sensing capability, as indicated, dmax=△. From a theoretical point of view, using ε1 defined as follows, the boundary conditions can be defined, which is also referred to as ε1-approximation approach.

From Figure 4, ϵ₁ is an arbitrarily sufficiently small positive number;  (or d_min) is a proper positive number to be chosen according to the constraint condition, physically, to avoid the collision between any two agents i and j, the minimum distance d₀ must be required, equivalently, the collision avoidance between any two agents i and j can be then guaranteed; d_k is the radius of feasible control area, which implies that two agents i and j can interact with each other, namely, the knowledge of agent j is available to agent i, thus the communication link e_k(v_i,v_j), v_i,v_j ∈ V and e_k ∈ E. Note that agent j may not need to acquire the information from agent i under the assumption on the directed graph, for instance, the relationship between two agents i and j is denoted by a single arrow; as a result, agent i has a limited information from the agents (or called the neighbors) that enter into its valid sensing area at time t, in view of this limited information, the control objective of this paper will be accomplished, and the dynamic nature of multi-agent system can be characterized. For this purpose, the following procedures are now presented.

With above results in hand, from a physical point of view, three constraint conditions are first provided as follows.

1. Collision avoidance. Collision avoidance is a critical issue for multi-agent system, there are a great number of control strategies that deal with collision problem. In this paper, we do not intend to propose a control method to solve this problem, for brevity, we here assume that the relationship between agents i and j is invalid if the actual distance $d_{ij}<d_{\min }$ , thus the collision problem is solved, it would be interesting to investigate this problem in future work.
2. Representation of dynamic edge. To investigate the dynamic nature of system, the edge effect is vital to the dynamic nature of system, the edge effect is characterized by an edge function (12), as mentioned above, the (12) is a time-varying and continuously weight function, i.e.,$\varphi (d_{ij})\in C^{\gamma }$ with $C^{\gamma }$ denoting the r^th-order continuous time derivative.
3. No interaction. Agents i and j has no limited information from each other in terms of different tasks, for example, to achieve and maintain the connectivity, or equivalently, agent i need to follow agent j at a certain instant t, if the actual distance $d_{ij}>d_{\max }$ , to be specific, in view of $d_{ij}=d_{ji}$ agent j is not within the feasible sensing area of agent i, that is to say, the link between two nodes i and j is broken, which does not imply the connectivity is not maintained for the whole system.

To proceed, to facilitate our analysis and derive the control laws, we can use the mathematical expression to denote the constraint conditions, from (12), thus its associated piece-wise function can be rewritten as follows

$\varphi \left(d_{ij}\right)=\{\begin{array}{cc}1,& d_{ij}\in \left[0,d_{\min }\right)\\ f\left(x\right),& d_{ij}\in \left[d_{\min ,d_k+{\in }_1}\right)\\ 0& d_{ij}\in \left[d_k+2\in ,\infty \right)\end{array}$ (15)

where $\varphi (d_{ij})$ is defined according to the geometrical constraint set (or the feasible set), which is shown in Figure 3(A).

From (15), if third case $\varphi (d_{ij})=0$ happens, it is hard to establish the edge between agents i and j as two agents move freely without any control input, the connectivity of the system is thus not guaranteed, to overcome this issue, the external control input u_i are needed, note that the u_e should be properly chosen as the continuous and bounded signals produced by the external force. Note that f(x) is a class of bump function, and the coefficient can be properly chosen such that 0 < f(x) < 1 as time goes to infinity, which is omitted here.

Substituting u_e into (11), yields

${\dot{p}}_i=u_{c,i}+u_{{}_{ei}}$ (16)

where u_c,i and u_e,i denote the Laplacian control input and external control input of agent i, respectively. Compared with (11), one can directly obtain ${\text{u}}_i=u_{c,i}+u_{e,i}$

The control objective of this paper is to maintain the algebraic connectivity L(λ₂), and its sufficient condition is guaranteed if ${\lambda }_2(L)>0,{\lambda }_2(L)$ is a function of states of agents as edges vary with time. As indicated, agent i has the knowledge about positions $p_i\in R^n$ , i.e., the relative measurements and magnitudes (or distances) of relative positions.

To proceed, we suppose the minimum value of quantity ${\lambda }_2={\in }_2$ with ${\in }_2$ denoting an arbitrary small positive number. As is customary, the exact value of the quantity is not obtained directly, but we can get the estimates of second eigenvalues by using following rules

${\widehat{\lambda }}_2-{\lambda }_2=\pm {\in }_{\lambda }$ (17)

where ϵ_λ is sufficiently small positive number, the interested reader can consult the material [5] for more details.

In terms of (5), which is also referred to as the potential function (or energy function), we obtain

$V({\lambda }_2)=V({\widehat{\lambda }}_2\pm \frac{\in \lambda }{2})$ (18)

Note that $V({\lambda }_2)\in R^{+}$ is continuously differentiable.

In order to guarantee the algebraic connectivity maintenance of the graph, the control strategy is derived using the negative gradient descent of $V({\lambda }_2)$ . Using the chain rule, we then take first time derivative of $V({\lambda }_2)$ with respect to agent p_i, one obtains

$\dot{V}({\lambda }_2)=\frac{\partial V({\lambda }_2(p))}{\partial p_{i,k}}=$$\frac{\partial V({\lambda }_2(p))}{\partial ({\lambda }_2(p)}\frac{\partial ({\lambda }_2(p)}{\partial p_{i,k}},i,k\in \{1, 2, \mathrm{....} n\}$ (19)

where p_{i, j} is k^th component of p_i. Thus, the composite control strategy of agent i is derived as follows

$u_{i=-}\dot{V}({\lambda }_2)$ (20)

In this section, we investigate the stability properties of the system. As discussed, the control law for agent i is proposed as follows

${\dot{p}}_{{}_i}=u_i^c+u_i^e$ (21)

where $u_i^c$ and $u_i^c$ are the control law and external control input, respectively. The external control input $u_i^c$ can be view as the additional task imposed on agent i. As before, notice that agent i will travel freely if $u_i^c$ =0, physically, no information interaction among agents, any connection between two agents may not be established, in other words, the results of connectivity preservation are not obtained, the proof is omitted due to page constraints. Moreover, since $u_i^c$ are bounded, p_i(t) are bounded for any initial positions p_i(0).

To fulfill the control objective, the control law is therefore considered. In what follows, we analyze the stability property of the system. To proceed, the following procedures are required and first stated formally.

1. Let $d_k(i,j)$ be the k^th, k ={1, 2, …, m} distance between agent i and j at time t, for brevity, we drop the quantity of time t, then $d_k(I,j)$ has the properties characterized as before, which can be viewed as a function of states p_i and p_j, namely,

$d_k(i,j)=\Vert p_i-p_j\Vert$ (22)

2. Taking the first derivative of d_k (i, j) with respect to p_i, we obtain

$\begin{array}{l}\frac{\partial {\text{d}}_{\text{k}}\text{(i, j)}}{{\text{p}}_{\text{i}}}=\frac{\partial ({\text{p}}_{\text{i}}-{\text{p}}_{\text{j}})}{{\text{p}}_{\text{i}}}({\text{p}}_{\text{i}}-{\text{p}}_{\text{j}})d_k^{-1}(i, j)\\ =({\text{p}}_{\text{i}}-{\text{p}}_{\text{j}})d_k^{-1}(i, j)\end{array}$ (23)

Where $d_k^{-1}(i, j)=\frac{1}{d_k(i, j)}, \frac{\partial {\text{d}}_{\text{k}}\text{(i, j)}}{{\text{p}}_{\text{i}}}$ represents the gradient information, which is called the limited information as d_k(i, j) is valid on the feasible sensing area defined by proximity information graph, proximity graph for short.

3. Since p_i is a column vector, with a slight abuse of notation, denoted by ${\text{p}}_{\text{i}}={[\mathrm{...} , p_{{}_{i,k}}, \mathrm{...}]}^T$ , where p_i,k is the k^th component of p_i, and the superscript T is the transpose.

Taking the first derivative of dk(i, j) with respect to pi, one gets

$\frac{\partial d_k(i,j)}{p_i}=(p_{i,k}-p_{j,k})$ (24)

From (20), the first part of right hand side of (24) is obtained.

Similarly, using above results, both derivatives with respect to p_i and p_j,k of d_k(i, j) can be computed, respectively. To proceed, with above results in hand, we next define two sets of control laws and external controls as

$U_c=\{u_1^c,u_2^c,\mathrm{...},u_n^c\}\in R^{n\times n}$

and

$U_e=\{u_1^e,u_2^e,\mathrm{...},u_n^e\}\in R^{n\times n}$

Respectively note that U_e are unknown bounded external control tasks. In light of P, denoted by P={p₁, p₂,…, p_n}, thus the overall control laws can be given as

$\frac{\partial d_k(i,j)}{p_i}=(p_{i,k}-p_{j,k})$ (25)

From (3), for simplicity, we omit the symbols (V, E), then the decentralized control laws are given as

$U_c=(L\otimes I_{n\times n})P$ (26)

where I_n×n is a n×n identity matrix.

As indicated, we define the energy function as V(p_i, p_j), it is noted that V(p_i, p_j), j∈N_i >0. Taking the first time derivative of V (p_i, p_j) w.r.t p_i, one obtains

$\begin{array}{l}V({\dot{p}}_i,p_j)=\frac{\partial V(p_i,p_j)}{\partial p_i}+{\displaystyle \sum _{i=1}^n{p}_i^T}L{\dot{p}}_i\\ ={\varphi }_u(p)+{\varphi }_e(p)\end{array}$ (27)

where

${\varphi }_u(p)=-{\displaystyle \sum _{i=1}^n{p}_i^T}{L}^2{\dot{p}}_i$ (28)

and

${\varphi }_e(p)={\displaystyle \sum _{i=1}^n{p}_i^T}L{u}_e^i$ (29)

where the capital letter T remains the same as before.

To proceed, the valuable property is introduced and stated formally as follows. Let A_n×n ∈ R^n×n and B_n×n ∈ R^n×n be two matrices, we have the $\Vert A\Vert \times \Vert B\Vert <=\left|\left|AB\right|\right|$ proof is straightforward and omitted here. Using above results, we have

${\varphi }_u(P)<=-{\displaystyle \sum _{i=1}^n\left|\right|L{p}_i|{|}^2}$ (30)

and similarly

${\varphi }_e(p)<={\displaystyle \sum _{i=1}^n\Vert L{p}_i\Vert }\Vert {\mu }_e^i\Vert$ (31)

Thus

${\varphi }_u(p)+{\varphi }_e(p)<=-{{\displaystyle \sum _{i=1}^n\Vert L{p}_i\Vert }}^2+{\displaystyle \sum _{i=1}^n\Vert L{p}_i\Vert }\Vert u_e^i\Vert$ (32)

For simplicity, it is noticed that we have dropped the dependence on time t for each term in the above. Let be ${\varphi }_{\{u,e\}}(i,t)$ expressed by

${\varphi }_{\{u,e\}}(i,t)=-{\Vert L{p}_i\Vert }^2+\Vert L{p}_i\Vert \Vert {\mu }_e^i\Vert$ (33)

By factoring out the term $\Vert L{p}_i\Vert$ , we obtain

${\varphi }_{\{u,e\}}(i,t)=-\left|\right|L{p}_i\left|\right|(|\left|L{p}_i\right||-|\left|u_e^i\right||)$ (34)

As a result,

$\dot{V}(p_i,p_j)<={\displaystyle \sum _{i=1}^n{\varphi }_{\{u,e\}}(i,t)}$ (35)

As indicated, the external control term${\mu }_e^i$ is bounded, let the maximum magnitude of ${\mu }_e^i$ be $\overline{\sigma }$ , then we have $\overline{\sigma }<\infty$ , which means that ${\varphi }_{\{u,e\}}(i,t)<2{\overline{\sigma }}^2,i\in \{1,\mathrm{...},n\}$ as time t approaches to infinity. According to the Lyapunov stability theory, one gets

$\{\begin{array}{l}V(p_i,p_j)>=0;\\ \dot{V}(p_i,p_j)<=0.\end{array}$ (36)

implying that $\Vert L{p}_i(t)\Vert >\overline{\sigma }$ for any i = {1,2,…,n}, therefore, ${\varphi }_{\{u,e\}}(i,t)<0$ .

Suppose the graph is connected, which means that the second smallest eigenvalue is bigger than zero, i.e., . Moreover, the quantity λ_L depends on the states of the agents, specifically, which is a non-decreasing function of the edge weights. We then have

$\Vert L{p}_i\Vert >={\lambda }_2(L)\Vert p^X\Vert$ (37)

where p is any vector, and X is a matrix such that $1_n^{T}X=0$ and $X^{T}X=1_{n-1}.L\in R^{n\times n}$ is the symmetric graph Laplacian matrix.

Since the sensing distance for each agent t is limited, we have that $d_{ij}\to d_{\max }$ as t tends to the instant t*, i.e., t→t*, which means that each agent i can converge to the specified position, denoted by p_i → p_id. See [5] for more detail treatment.

Using above results, the extension to the consensus control of multi-agent systems is also discussed here. In this setting, the external control for each agent is neglected, and the initial positions of agents are generated randomly, in particular, which characterizes the stable equilibrium of a team of agents. As a consequence, the overall control law for the system is given as

$u_o=-\nabla V_o(p_i-p_j),j\in N_i$ (38)

where V_o is a Lyapunov candidate function $\nabla V_0$ ,is the gradient of V_o.

In this section, several simulation results are provided to validate the obtained theoretical results. Consider the multi-agent system consists of 7 agents, and suppose no any control law that imposed on the seventh agent, then the agent 7move freely with any given arbitrary trajectory, that is

$u_{i,e}=\{\begin{array}{l}(1+i*Inc)*\cos (t);\\ (1+i*Inc)*sin(t).\end{array}$ (39)

where Inc is an increment quantity, we select Inc=0.25, for all i = [1, 2, 3, 4, 5, 6, 7].

To implement the control law for each agent, the initial positions is first given randomly as follows:

$P_i(0)=\{\begin{array}{l}{\text{p}}_{\text{1}}\text{(0) = [-2}\text{.50; 0}\text{.58]}\\ {\text{p}}_{\text{2}}\text{(0) = [1}\text{.35; 0}\text{.78]}\\ {\text{p}}_{\text{3}}\text{(0) = [-1}\text{.50;-2}\text{.90]}\\ {\text{p}}_{\text{4}}\text{(0) = [0}\text{.15;-0}\text{.48]}\\ {\text{p}}_{\text{5}}\text{(0) = [-2:60; 5}\text{.60]}\\ {\text{p}}_{\text{6}}\text{(0) = [5}\text{.70;-2}\text{.30]}\\ {\text{p}}_{\text{7}}\text{(0) = [0}\text{.80;-3}\text{.12]}\end{array}$ (40)

which is shown in Figure 5.

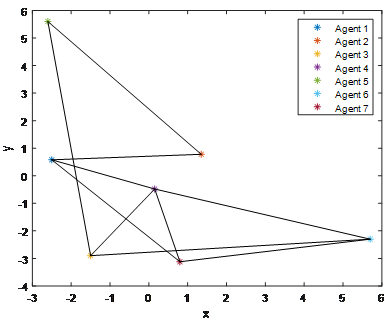
Figure 5 The initial positions for the agents.

From Figure 6, except the seventh agent, other agents can converge to stable point under the control laws. Any two agents in six agents can be connected with each other, while the seventh agent does not have any connection with other agents if only external control is considered. To achieve the overall connectivity maintenance, it is necessary to show that the control law is needed, which is illustrated in Figure 7. The application to formation control problem is also considered, where the proposed control law depends on the local measurements, which is illustrated in Figure 8, which shows that all agents can converge to the stable equilibrium under the proposed control law, i.e., the desired formation control is achieved.

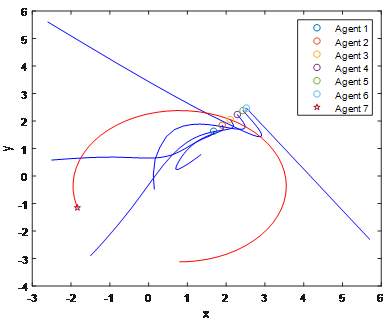
Figure 6 Trajectories of seven agents in the plane. Assume no controller is designed only for the seventh agent, while other agents move under the proposed control law, i.e., the seventh agent have no any interaction from the other agents, thus the connectivity is not maintained, which is illustrated by two red curves.

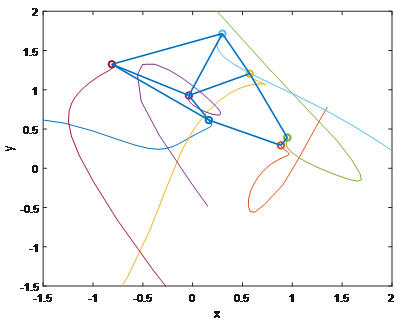
Figure 7 Connectivity maintenance is achieved for the seven agents in the plane.

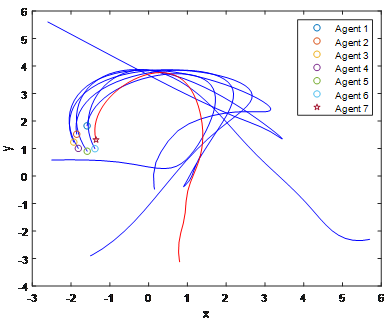
Figure 8 Formation control with seven agents, the connectivity is maintained.

In general, the algebraic connectivity can be viewed as the second largest eigenvalue of Laplacian matrix λ₂(L), and λ₂(L) is a continuously differentiable function, which consists of all information states of all agents, though the knowledge of λ₂(L) is not computed directly by each agent, λ₂(L) can be calculated by using the optimization algorithm for each agent. In addition, the time-varying weight ${\omega }_{ij}$ that imposed on each edge e_ij ∈ E between any two agents i and j is defined as a piecewise function under the proximity graph mentioned above. Based on above results, we conclude that the algebraic connectivity can be maintained by implementing the proposed control law.

In this paper, we investigate the connectivity maintenance problem for multi-agent system; each agent is described with a single integrator. Using local and limited communication information, we first establish the Lyapunov function, then the decentralized control is derived. To achieve the group objective, each information state must be provided and a common control protocol should be obeyed, which implies that each agent must communicate with the rest of agents as time evolves, then the connectivity can be maintained and connected network of a team of agents can be established.

This work is supported by the National Natural Science Foundation of China under Grant No.61402540, No.60903222, No.61672538, and No.61272024, Hunan Provincial Science and Technology Foundation No. 2014GK3049.

We declare that there is no conflicts of interest.

1. Lorenzo Sabattini, Cristian Secchi, Matteo Cocetti, et al. Implementation of coordinated complex dynamic behaviors in multirobot systems. IEEE Transactions on Robotics. 2015;31(4):1018–1032.
2. Donato Di Paola, Andrea Gasparri, David Naso, et al. Decentralized dynamic task planning for heterogeneous robotic networks. Autonomous Robots. 2015;38(1):31–48.
3. Derya Aksaray A, Yasin Yazıcıoglu, Eric Feron, et al. Message-passing strategy for decentralized connectivity maintenance in multiagent surveillance. Journal of Guidance Control, and Dynamics. 2015.
4. Hasan Poonawala A, Aykut Satici C, Hazen Eckert, et al. Collision-free formation control with decentralized connectivity preservation for nonholonomic-wheeled mobile robots. IEEE Transactions on control of Network Systems. 2015;2(2):122–130.
5. Hasan A Poonawala, Mark W Spong. Preserving Strong Connectivity in Directed Proximity Graphs. IEEE Transactions on Automatic Control. 2017.
6. Zhihua Qu, Chaoyong Li, Frank Lewis. Cooperative control with distributed gain adaptation and connectivity estimation for directed networks. International Journal of Robust and Nonlinear Control. 2014;24(3):450–476.
7. Angelia Nedic, Alex Olshevsky. Distributed optimization over time-varying directed graphs. IEEE Transactions on Automatic Control. 2015;60(3):601–615.
8. Paolo Di Lorenzo, Sergio Barbarossa. Distributed estimation and control of algebraic connectivity over random graphs. IEEE Transactions on Signal Processing. 2014;62(21):5615–5628.
9. Miroslav Fiedler. Algebraic connectivity of graphs. Czechoslovak mathematical journal. 1973;23(2):298–305.
10. Maria Carmela De Gennaro, Ali Jadbabaie. Decentralized control of connectivity for multi-agent systems. Decision and Control, 2006 45th IEEE Conference. 2006;3628–3633.
11. Florian Knorn, Rade Stanojevic, M Corless, Robert Shorten. A framework for decentralised feedback connectivity control with application to sensor networks. International Journal of Control. 2009;82(11):2095–2114.
12. Kunal Srivastava, Angelia Nedic. Distributed asynchronous constrained stochastic optimization. IEEE Journal of Selected Topics in Signal Processing. 2011;5(4):772–790.
13. Jorge Cortes, Sonia Martinez, Francesco Bullo. Robust rendezvous for mobile autonomous agents via proximity graphs in arbitrary dimensions. IEEE Transactions on Automatic Control. 2006;51(8):1289–1298.
14. Cosimo Federico Ardito, Donato Di Paola, Andrea Gasparri. Decentralized estimation of the minimum strongly connected subdigraph for robotic networks with limited field of view. Decision and Control (CDC), 2012 IEEE 51st Annual Conference. 2012;5304–5309.
15. Mengmeng Xu, Qinghai Yang, Kyung Sup Kwak. Algebraic connectivity aided energy-efficient topology control in selfish ad hoc networks. Wireless Networks. 2017;23(5):1331–1341.
16. Michael M Zavlanos, Magnus B Egerstedt, George J Pappas. Graph-theoretic connectivity control of mobile robot networks. Proceedings of the IEEE. 2011;99(9):1525–1540.
17. Dimos V Dimarogonas, Karl H Johansson. Bounded control of network connectivity in multi-agent systems. IET control theory & applications. 2010;4(8):1330–1338.
18. Fabio Morbidi, Antonio Giannitrapani, Domenico Prattichizzo. Maintaining connectivity among multiple agents in cyclic pursuit: A geometric approach. Decision and Control (CDC), 2010 49th IEEE Conference. 2010;7461–7466.
19. Lorenzo Sabattini, Nikhil Chopra, Cristian Secchi. Decentralized connectivity maintenance for cooperative control of mobile robotic systems. The International Journal of Robotics Research. 2013;32(12):1411–1423.
20. Andrea Gasparri, Lorenzo Sabattini, Giovanni Ulivi. Bounded Control Law for Global Connectivity Maintenance in Cooperative Multirobot Systems. IEEE Transactions on Robotics. 2017;33(3):700–717.
21. Minh Hoang Trinh, Kwang-Kyo Oh, Kyungmin Jeong, Hyo-Sung Ahn. Bearing-only control of leader first follower formations. IFAC-PapersOnLine. 2016;49(4):7–12.
22. Paolo Robuffo Giordano, Antonio Franchi, Cristian Secchi, Heinrich H Bulthoff. A passivity-based decentralized strategy for generalized connectivity maintenance. The International Journal of Robotics Research. 2013;32(3):299–323.
23. Lorenzo Sabattini, Cristian Secchi, Nikhil Chopra. Decentralized control for maintenance of strong connectivity for directed graphs. Control & Automation (MED), 2013 21st Mediterranean Conference. 2013;978–986.
24. Ali Jadbabaie, Nader Motee, Mauricio Barahona. On the stability of the Kuramoto model of coupled nonlinear oscillators. American Control Conference, 2004. Proceedings. 2004;5:4296–4301.
25. Peng Yang, Randy A Freeman, Geoffrey J Gordon, et al. Decentralized estimation and control of graph connectivity for mobile sensor networks. Automatica. 2010;46(2):390–396.