The present article investigates a chaotic convection under modulation in the presence of internal heat generation. The viscoelastic fluid saturating porous medium, heated from below is considered; a modified Darcy’s momentum equation and heat generation term used in energy equation. An autonomous system of fourth order differential equations have been deduced by using truncated Galerkin expansions. The asymptotic behavior can be stationary, periodic, or chaotic, depending upon the values of system parameters. It is found that a better combination of values of modulation parameters and scaled Rayleigh, internal Rayleigh numbers provides a way for chaos. Both a temperature and gravity modulation of the medium is to enhance or diminish the behavior of chaotic nature of the system. Due to high internal heat generation there is a chance to devolve a new kind of stable or unstable points in the system. Finally, heat transfer results are presented in terms of Nusselt number.

Keywords: Internal heating, g-jitter effects, chaotic convection, lorentz system

Latin Symbols

g, Acceleration due to gravity; d, Depth of the porous media; (x, z), Horizontal and vertical co-ordinates; Q, Internal heat source; R_i, Internal Rayleigh number $R_i=\frac{Q{d}^2}{k_T}$ ; k, Permeability; Pr_D, Prandtl-Darcy number $P{r}_{{}_D}=\frac{\delta \nu d^2}{K{k}_T}$ ; p, Reduced pressure; Pr, caled Prandtl-Darcy number $Pr=\frac{P{r}_D\gamma }{{\pi }^2}$ ; R, Scaled Rayleigh number $R=\frac{a^{2}Ra}{{\left(a^2+{\pi }^2\right)}^2}$ ; T, Temperature; ∆T, Temperature difference across the porous layer; Ra, Thermal Rayleigh-Darcy number,$Ra=\frac{\beta Tg\Delta TdK}{vkT}$ ; T, Time; a, Wave number. 

Greek Symbols

${\delta }_2$ , Amplitude of gravity modulation;

${\delta }_1$ , Amplitude of temperature modulation;

${\alpha }_T$ ,Coefficient of thermal expansion;

µ, Dynamic viscosity of fluid;

$k_T$ ,Effective thermal diffusivity;

$\rho$ ,Fluid density;

${\Omega }_2$ ,Frequency of gravity modulation;

${\Omega }_1$ ,Frequency of temperature modulation;

 ν, Kinematic viscosity,  ;

 Γ, Non-dimensional relaxation time;

 φ, Phase angle;

 δ, Porosity;

 Γ, Ratio of retardation time to relaxation time, ;

ψ, Stream function;

${\overline{\lambda }}_1$ , Stress relaxation time;

${\overline{\lambda }}_2$ , Strain retardation time;

 τ, Time (dimensionless).

Other symbols

${\nabla }^2$ , $\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}+\frac{{\partial }^2}{\partial z^2}$ Subscripts;

b, Basic state;

c, Critical;

0, Reference value.

Superscripts

*        Dimensionless quantity

‘         Perturbed quantity

The study of non-Newtonian fluids attracted tremendous interest in research because of its usage as a working media in many engineering and industrial applications. One of such a non- Newtonian fluids viscoelastic fluids exhibit both solid and liquid properties have applications in the fields as geothermal material processing, energy modeling, cooling of electronic devices, thermal insulation material, transport of chemical substances, crystal growth, solar receivers and injection molding. Other applications are found in the petroleum industry, nuclear and chemical industries, geophysics, bioengineering and so on. The relevant studies of viscoelastic fluids may be found in the studies of Bhadauria et al.,^1‒3 the corresponding introduction there in. The concept of chaotic convection in porous medium has received great interest due to its applications in industry and atmospheric sciences. A fundamental characteristic of a chaotic model is its extreme sensitivity to its initial conditions; i.e. small difference in the initial state can lead to extraordinary difference in the system state. Chaotic behaviour is complex, irregular and in mechanical systems, generally this nature is undesirable. For examples, to design electric circuits, mechanical devices, signals, stabilizing the lasers and other industrial systems are governed by chaos in engineering and industry. The thermal insulation, thermal energy utilization and dynamics of satellites are examples of chaos in nature. In other many practical mechanical applications, improved system performance or the avoidance of fatigue failure requires controlling the system, so that chaos is removed or leading the system stable and predictable behaviour. Therefore, within the nonlinear dynamics research area, the control- ling or ordering of chaos is increasing attention. In the field of chaos analysis and control, the Lorentz system is considered a paradigm, since it captures many of the future of the chaotic dynamics. The concept of chaos was first introduced by Poincare^4,5 who investigated orbits in celestial mechanics and realized that the dynamical system generated by the three body problem is quite sensitive to the initial conditions exhibiting chaotic behavior. Since the introduction of the chaotic attractors by Lorenz,⁶ is to study the atmospheric convection. Many chaotic systems have been introduced, such as the Rossler,⁷ the Chen⁸ and the Lu⁹ systems. Related and relevant studies on chaotic convection investigated by numerous authors to see the dynamics of the nonlinear system towards its initial disturbances; some of them are.^10‒25 The study of heat transfer with internal heat sources arises at consideration of heat dissipation in porous layers exposed to radioactive radiation at storage of nuclear waste materials or transmitting high energy particle beams. The wide range applications occur in nuclear re- actions, nuclear heat cores, nuclear energy, nuclear waste disposals, oil extractions, and crystal growth. The heat transfer in a window for transmission of high-energy beams with a metal foam porous layer is studied by Hetsroni et al.²⁶ They found that, the high performance of the metal foam heat sinks for cooling such windows. The image processing of thermal maps on the surface of open-cell porous layer revealed that boundary condition with constant heat flux became more relevant for numerical model than those with constant temperature at high values of Reynolds numbers based on the permeability. The studies related to internal heat generation recently investigated.^27‒31 In most of the above research papers regarding Lorentz chaos control, it is considered essential to know the Lorentz model parameters for the successful derivation of a control. Further, it is often assumed in many papers that the system is without external disturbances. In a practical most of the situations, the parameters of the Lorentz chaotic system may not be known, may be varying in time and may be undergoing either match or mismatch disturbances. Thus, the derivation of a chaos controller for a Lorentz system in the presence of parameter uncertainty and disturbances is an important problem. Vadasz et al.,³² have investigated the effect of vertical vibrations on chaotic convection in porous medium employing Darcy model. Their results show that periodic and chaotic solutions alternate as the value of the scaled Rayleigh number varies under gravity modulation.^33‒37 Further, they also concluded that the neglect of the time derivative in the original Darcy equation is not justified when vibrations and wave effects are being considered. Kiran et al.,³⁸ studied oscillatory and chaotic mode of convection in a magnetic two component fluid layer, and investigated heat, mass transfer and the chaotic nature of the problem. They found that, oscillatory mode of convection enhances heat, mass transfer than the stationary mode of convection due to interaction of oscillatory frequency with amplitude of convection. Also their results of gravity modulation stimulates on the dynamics of the current model and declares that, a suitable combination of the choice of the values of frequency and amplitude of modulation one may have control on chaos. Bhadauria et al.,³⁹ was the first who investigated temperature modulation^40‒44 effect on chaotic convection of the problem. Their results show that, the transition from steady to chaotic nature can be controlled by three types of temperature modulation while choosing the suitable values of amplitude and frequency. The present paper investigates (while considering the studies of ([?])) the chaotic convection under temperature and gravity modulations in the presence of internal heat source.

A viscoelastic fluid saturated horizontal porous medium, confined between two parallel infinitely extended horizontal planes at z=0 and z=d, a distance‘d’ apart, has been considered. A Cartesian frame of reference is chosen in such a way that the origin lies on the lower plane and the z-axis as vertical upward. Oberbeck-Boussinesq approximation is applied to account the effect of density variations. The non-Newtonian behavior of the viscoelastic fluid is characterized using the Oldroyd model. Under these conditions the governing equations for thermal convection in a viscoelastic fluid saturated porous medium are given by:

$\nabla .\overrightarrow{q}=0,$     (2.1)

$\left(1+{\overline{\lambda }}_1\frac{\partial }{\partial t}\right)\left(\frac{{\rho }_0}{\delta }\frac{\partial \overrightarrow{q}}{\partial t}+\nabla P-\rho \overrightarrow{g}\right)+\frac{\mu }{K}\left(1+{\overline{\lambda }}_2\frac{\partial }{\partial t}\right)\overrightarrow{q}=0$     (2.2)

$\frac{\partial T}{\partial t}+\left(\overrightarrow{q}.\nabla \right)T=\text{}{K}_T{\nabla }^{2}T+Q\left(T-T_0\right)$     (2.3)

$\rho ={\rho }_0\left[1-{\alpha }_T\left(T-T_0\right)\right]$     (2.4)

Where, the physical variables have their usual meanings and are given in Nomenclature. The externally considered thermal boundary conditions are given by Venezian⁴⁰:

$T=T_0+\frac{\Delta T}{2}\left[1+{\delta }_1\cos \left(\Omega t\right)\right]$ ,at z = 0

$=T_0-\frac{\Delta T}{2}\left[1-{\delta }_1\cos \left(\Omega t+\theta \right)\right]$ , at z = d     (2.5)

Where ∆T is the temperature difference across the porous medium, δ₁, Ω₁ are the amplitude and frequency, θ is the phase angle of temperature modulation. The externally imposed gravitational field is given by Gresho et al.³³:

$\overrightarrow{g}=g_0\left[1+{\delta }_{2}cos\left({\Omega }_{2}t\right)\right]\widehat{k}$     (2.6)

Where δ₂, Ω₂ are the amplitude and frequency of gravity modulation

Basic state

The basic state is assumed to be quiescent and the physical variable in this state are given by:

${\overrightarrow{q}}_{{}_b}=0,p=p_{{}_b}\left(z,t\right),T=T_{{}_b}\left(z,t\right),\rho ={\rho }_{{}_b}\left(z,t\right)$     (3.1)

Substituting Equation (3.1) in Equations (2.1)-(2.4), we get the following equations which are used to determine the basic state pressure and temperature:

$\frac{\partial p_{{}_b}}{\partial z}=-{\rho }_{{}_b}\overrightarrow{g}$     (3.2)

$\frac{\partial T_b}{\partial t}=K_T\frac{{\partial }^2{T}_b}{\partial z^2}+Q\left(T_b-T_0\right)$     (3.3)

${\rho }_{{}_b}={\rho }_0\left[1-{\alpha }_T\left(Tb-T0\right)\right]$     (3.4)

The solution of the Equation (3.3), subjected to the thermal boundary conditions given in Equation (2.5), is given by

$T_b\left(z,t\right)=T_s\left(z\right)+{\delta }_{1}Re\left[T_1\left(z,t\right)\right]$     (3.5)

The finite amplitude perturbations on the basic state are superposed in the form:

$\overrightarrow{q}={\overrightarrow{q}}_b+q^{\prime },\rho ={\rho }_b+{\rho }^{\prime },p=p_b+p^{\prime },T=T_b+T^{\prime }$     (3.6)

Introducing the Equation (3.6), the basic state temperature field in Equation (2.1)-(2.4), and then use the stream function ψ as $u^{\prime }=\frac{\partial \psi }{\partial z},w^{\prime }=-\frac{\partial \psi }{\partial x},$ for two dimensional flow. The equations are then non-dimensionalized using the physical variables;

$\left(x,y,z\right)=d(x^{\ast },y^{\ast },z^{\ast })$ ,$t=\frac{d^2}{K_T}t*$ ,$\psi =K_T\psi *$ ,$T^{\prime }=\Delta TT*$ , ${\lambda }_2=\frac{K_T{\overline{\lambda }}_2}{d^2},p^{\prime }=\frac{\mu K_T}{L}p*$ ${\lambda }_1=\frac{K_T{\overline{\lambda }}_1}{d^2}$ ,and $\Omega =\frac{K_T}{d^2}\Omega *$ . The resulting non-dimensionalized system of equations can be expressed as (dropping the asterisk)

$\left[\frac{1}{Va}\left(1+{\lambda }_1\frac{\partial }{\partial t}\right)\frac{\partial }{\partial t}+\left(1+{\lambda }_2\frac{\partial }{\partial t}\right)\right]{\nabla }^2\psi =-Ra\left(1+{\lambda }_1\frac{\partial }{\partial t}\right)\frac{\partial T}{\partial x}$     (3.7)

$-\frac{\partial T_b}{{\partial }_z}\frac{\partial \psi }{\partial x}+\left(\frac{\partial }{\partial t}-{\nabla }^2-R_i\right)T=\frac{\partial \left(\psi ,T\right)}{\partial \left(x,z\right)}$     (3.8)

Where, $R_a=\frac{{\alpha }_{T}g\Delta TKd}{vKT}$ is thermal Darcy-Rayleigh number, $v=\frac{\mu }{{\rho }_0}$ is kinematic viscosity. The basic state temperature which appears in Equation (3.8) is given by:

$\frac{\partial T_b\left(z,t\right)}{\partial z}=f_1\left(z\right)+{\delta }_1{\mathrm{R}}_e\left[f_2\left(z,t\right)\right]$     (3.9)

Where,

$f_1\left(z\right)=-\frac{\sqrt{R_i}}{2\sin \sqrt{R_i}}\left(\cos \sqrt{R_i}\left(1-z\right)+\cos \sqrt{R_i}\left(z\right)\right)$     (3.10)

$f_2\left(z,t\right)=\left(\left\{a_1\left(\zeta \right)e^{\zeta z}+a_1\left(-\zeta \right)e{-}^{\zeta z}\right\}{e}^{-i\Omega t}\right)$     (3.11)

Where, $a_1=\frac{\zeta }{2}\frac{\left(e^{-i\theta }-e^{-\zeta }\right)}{\left(e^{\zeta }-e^{-\zeta }\right)}$ and $\zeta =\sqrt{-I\Omega -R_i}$ Here f₁ is the steady part, and f₂ is an oscillatory part of the basic state temperature T_b. The effect of temperature modulation and internal heating enters through the factor $\frac{\partial T_b}{\partial z}$ which is obtained from the Equation (3.9). To obtain the solution of the nonlinear coupled system of partial differential Equations (3.7-3.8), we represent the stream function and temperature in the following Fourier series expressions.^{13,32,39,45,46}:

$\psi =A_{11}\sin \left(ax\right)\sin \left(\pi z\right)$     (3.12)

$T=T_b+B_{11}\cos \left(ax\right)\sin \left(\pi z\right)+B_{02}\sin \left(2\pi z\right)$     (3.13)

Where, the unknown amplitudes A₁₁ (t), B₁₁ (t), B₀₂ (t) are the functions of time t. Substituting the expressions (3.12) - (3.13) in equations (3.7) - (3.8), taking the orthogonality condition with the eigenfunctions associated with the Eqs. (3.12-3.13), and integrating them over the domain yields a set of three ordinary differential equations for the time evolution of the amplitudes, in the form:

$\left(\left(1+\Gamma \frac{\partial }{\partial t}\right)+Va\left(1+\Gamma \Lambda \frac{\partial }{\partial t}\right)\right)A_{11}=\frac{aVaRa}{{\pi }^2+a^2}\left(1+\Gamma \frac{\partial }{\partial t}\right)B_{11}$     (3.14)

$\left({\pi }^2+a^2\right)\frac{d{B}_{11}}{dt}-2a{I}_1{A}_{11}=a\pi A_{11}{B}_{02}+\left(R_i-\left({\pi }^2+a^2\right)\right)B_{11}$     (3.15)

$\left({\pi }^2+a^2\right)\frac{d{B}_{02}}{dt}=-\left(4{\pi }^2-Ri\right)B_{02}-\frac{a\pi }{2}{A}_{11}{B}_{11}$     (3.16)

Where, the time has been re-scaled and the following notations are introduced $t=\left(a^2+{\pi }^2\right)\tau$,$I_1={\displaystyle \underset{0}{\overset{1}{\int }}\frac{\partial T_b}{\partial z}}{\sin }^2\left(\pi z\right)dz$ and ${\Omega }_1=\frac{1}{\left(a^2+{\pi }^2\right)}\Omega$ . It is convenient to introduce the following further notations: $R=\frac{a^{2}Ra}{{\left(a^2+{\pi }^2\right)}^2}$ ,$\mathrm{Pr}=\frac{Va}{\left(a^2+{\pi }^2\right)},$ $X=\frac{a\pi A_{11}}{\left(a^2+{\pi }^2\right)\sqrt{2}},$ $Y=\frac{\pi R{B}_{11}}{\sqrt{2}},$ and $Z=-\pi R{B}_{02}$ to get the following set of scaled equations which are equivalent to Eqs. (3.14-3.16):

$\dot{X}=W$     (3.17)

$\dot{Y}=dX+eY-XZ$     (3.18)

$\dot{Z}=\frac{\left(R_i-4{\pi }^2\right)}{\left(a^2+{\pi }^2\right)}Z+XY$     (3.19)

$\dot{W}=\mathrm{Pr}\left(\left(d+{\Gamma }^{-1}\right)X+\left(e+{\Gamma }^{-1}\right)Y-XZ-\left(\Lambda +\frac{1}{\mathrm{Pr}\Gamma }\right)W\right)$     (3.20)

Where, $d=-R{I}_1$ . Now substituting $U=Y-\Lambda X–\frac{W}{\mathrm{Pr}}$ in the above system of Eqs.(3.17-3.20), then obtain the following equations:

$\dot{X}=\mathrm{Pr}\left(Y-\Lambda X-U\right)$ (    3.21)

$\dot{Y}=dX+eY-XZ$     (3.22)

$\dot{Z}=\frac{\left(R_i-4{\pi }^2\right)}{\left(a^2+{\pi }^2\right)}Z+XY$     (3.23)

$\dot{U}={\Gamma }^{-1}\left[\left(1-\Lambda \right)X-U\right]$     (3.24)

Suppose for Newtonian fluids while taking Γ → 0, Λ → 0 and R_i → 0 in the system of Equations (3.17-3.20), the famous Lorenz⁶ problem is obtained. In addition, for the above case if one let P_r → ∞, then Akhatov et al.,⁴⁷ system will be arrived. 

Stability analysis

Equilibrium points setting the time derivatives of the system Equations (3.17-3.20) to vanish, obtain the equilibrium points for velocity and temperature fields as (for un-modulated case)

$X_1=Y_1=Z_1=W_1=0$     (4.1)

Which corresponds to the motionless solution or pure heat conduction solution, the other two equilibrium points (corresponding to the convection solution) are

$\left[X_{2,3},Y_{2,3},Z_{2,3},W_{2,3}\right]=\left[\pm c,\pm c,\left(e-d\right),0\right]$     (4.2)

Where $C=\sqrt{\frac{\left(R_i-4{\pi }^2\right)}{\left(a^2+{\pi }^2\right)}\left(d-e\right)}$ .

The stability of the fixed points corresponding motionless solution is governed by the roots of the following characteristic polynomial equation (obtained from the Jacobian matrix of system Equations (3.17-3.20)) for the Eigen values of:

$\left(c-\lambda \right)\left[{\lambda }^3+\left(\left(Pr\Lambda +{\Gamma }^{-1}\right)-e\right){\lambda }^2+\left(Pr\left(d+{\Gamma }^{-1}\right)–e\left(Pr\Lambda +{\Gamma }^{-1}\right)\right)\lambda +Pr\left(2ed+\left(e+d\right){\Gamma }^{-1}\right)\right]=0$     (4.3)

Where, $e=\frac{\left(R_i-\left({\pi }^2+a^2\right)\right)}{\left({\pi }^2+a^2\right)}$ Stability depends on the values of Γ, for $\Gamma <\frac{\mathrm{Pr}-e}{\mathrm{Pr}e\left(\Lambda -1\right)}$ there is an exchange of stability, and for other two steady state solutions origin loses its stability. When $\Gamma >\frac{\mathrm{Pr}-e}{\mathrm{Pr}e\left(\Lambda -1\right)}$ , there is a pair of pure imaginary roots of Equation 4.3. The oscillatory or over stable solutions are arises at a critical value of Rayleigh number given by

$R^{osc}=\frac{{\left(a^2+{\pi }^2\right)}^2\left(4{\pi }^2-R_i\right)\left(1+Pr\Gamma \Lambda \right)\left[e\left(1+Pr\Gamma \Lambda \right)-Pr\left(1+e\Gamma \right)–e^2{\Gamma }^2\left(Pr\Lambda -e\right)\right]}{4{\pi }^2{a}^{2}Pr\left(1+e\Gamma \right)\left(Pr\Lambda -e\right)}$     (4.4)

The stability of the fixed point corresponding to convection solution is governed by the roots of the following characteristic polynomial equation for the eigen values,

${\lambda }^4+\left[\left(Pr\Lambda +{\Gamma }^{-1}\right)-\left(e+c_1\right)\right]{\lambda }^3+\left[c_{1}d-\left(e+c_1\right)\left(Pr\Lambda +{\Gamma }^{-1}\right)+Pr\left(e+{\Gamma }^{-1}\right)\right]{\lambda }^2$     (4.5)

$+[c_{1}d(Pr\Lambda +{\Gamma }^{-1})-Pr(e+{\Gamma }^{-1})(2e+c_1)+Pr{c}_1\left(d-e\right)]\lambda +2c_{1}ePe(e+{\Gamma }^{-1})=0$     (4.6)

Where $c_1=\frac{R_i-4{\pi }^2}{\left(a^2+{\pi }^2\right)}$ . The steady state solutions are useful because they predict that a finite amplitude solution to the system is possible for subcritical values of the Rayleigh number and that the minimum values of R for which a steady solution is possible lies below the critical values for instability to either a marginal state or an over stable infinitesimal perturbation. The above Equation (4.6) yields four eigen values, and all the roots are real and negative at slightly supercritical value of R, such that the convection fixed points are stable, that is simple nodes. These roots move on the real axis towards the origin as the value of R increases. The motionless solution loses stability and convection solution takes over when eigen values and become equal and complex conjugate when R=10.423452 (for thermal modulation) and R=14.2324567 (for gravity modulation) (these values evaluated numerically using the equation above Equation (4.6) with Mathematica). At this point the convection fixed points lose their stability and other (periodic or chaotic) solutions take over. The loss of stability of the convection fixed points for the corresponding system parameter values observed in the figures.

Gravity modulation

The non-dimensional governing equation takes the following form:

$\dot{X}={\mathrm{P}}_r\left[\left(1+{\delta }_2\sin {\Omega }_{2}T\right)Y-\Lambda X-U\right]$     (5.1)

$\dot{Y}=R\frac{4{\pi }^2}{\left(4{\pi }^2-R_i\right)}X+eY-XZ$     (5.2)

$\dot{Z}=\frac{\left(R_i-4{\pi }^2\right)}{\left(a^2+{\pi }^2\right)}Z+XY$     (5.3)

$\dot{U}={\Gamma }^{-1}\left[\left(1-\Lambda \right)X-U\right]$     (5.4)

Where δ₂ is the frequency and Ω₂ is the amplitude of gravity modulation.

Heat transfer

In the study of non-linear realm of convection in porous medium, the analysis of heat transport is important. Heat transfer is significant due to interaction of stream line flow with thermal diffusion which is raised due the Jacobian term in energy equation. In the steady state, heat transport takes place through conduction alone. Later on as time passes heat transfer becomes in the form of convection. The heat transfer coefficient Nusselt number (Nu) is defined as^24,39

The above system of Equations (3.17-3.20) are equivalent to Lorenz equations; Lorenz⁶ Sparrow¹⁵ with different coefficients. The demonstration of this equivalence was provided by Vadasz & Olek^12,13 and Kiran et al.³⁹ for unmodulated system.

Applying the constitutive equations of the Oldroyd model, we deduced the system (3.17-3.20) to describe the dynamics of thermal convection in a viscoelastic fluid-saturated porous medium. The above systems (3.17-3.20) of equations are solved using NDSolve Mathematica 8. The initial conditions used for all numerical solutions are τ = 0: X = Y = Z = 0.8 and W = 0.1. The parameter values for all numerical solutions are varied to observe the impact of each individual parameter under temperature and gravity modulation. This paper demonstrate the effect of modulation and internal heat source on the dynamic of the problem, in the form of space projections of trajectories onto the YX, ZX, ZY planes, as the value of various parameters varies for a particular range of time. Though numerous studies are available on chaotic convection, there is no study which deals with chaotic convection under the effect of internal hating under modulation. The results are presented here have been obtained numerically for a set of suitable parameter values and initial conditions Figure 1. The effect of modulations is investigated just before or after the critical values of R. The important concept is that, how this modulation has control over the transition from steady to chaos in the presence of internal heat source. Study of heat transfer is also investigated in the system in terms of Nusselt number.

Figure 1 Physical configuration of the problem.

At first the results corresponding to temperature modulation is discussed when both plates are in OPM case. The evolution of trajectories over time in the state space for increasing the values of scaled Rayleigh number R is presented in Figure 2, in terms of the projections of trajectories onto the plane. From the Figure 2 it is observed that, the trajectory moves to the steady convection point on a straight line for R slightly above the loss of stability of the motionless solution. As the value of R varies from 2 to 9 the trajectories approach the fixed point on a spiral as given in Figure 2b,2c. We observe in Figure 2d that, the transition to chaos at a critical value of R=10.364367, where it is the value after a solitary limit cycle indicating the loss of stability of the convection fixed points. In fact the detailed study of the behaviour of transition from steady to chaos due to the variation of R near its critical value investigated by Vadasz^14,47 and Sheu et al.²⁰ Vadasz et al.³² and Vadasz et al.⁴⁵ In Figure 3a for the critical value of R=10.364367 where the system loses its stable solution to convection solution under modulation, the effect of internal heating R_i=0.4223 is to encourage the system where the convection fixed points lose their stability and a chaotic solution takes over in the presence of modulation. But, when δ₁=0 (Figure 3b) for R_i=0.4223 and R=10.364367 (transition point under modulation), the system achieves its transition state. The effect of internal heating given Figure 4 for modulated system, as R_i varies positively from 0.1 to 0.6, the trajectories more vibrant spiral towards motionless solution and suddenly when R_i=0.8 the transition to chaotic solution occur. In Figure 5 the effect of internal heating is presented for unmodulated system and for lower values of R (steady state). This case is quite interest to see where, as internal heating varies positively from 0 to 4, the transition from steady state solution to un-steady chaotic solutions obtained though the system is under un-modulated. It is to be noted that for R_i>0 heat source and R_i<0 heat sink, i.e. for negative values of R_i=4 the achieves its steady state solution. With this one can conclude that, effect of internal heat source or sink may use to control chaotic nature of the solution of the system. The effect of Ω₁ fixing δ₁=1.5 presented in Figure 6. For the values of Ω₁=0.0 and 1.4, the solutions show steady behaviour towards one of the fixed point. Further, for higher values such as Ω₁=1.5, the chaotic behaviour of the solution is observed, the solution exhibits chaotic behaviour in time domain as well. This reveals the results of Kiran et al.,³⁹ according to them, a better or suitable choice of values of modulation parameters one can get control over the dynamic of the problem.

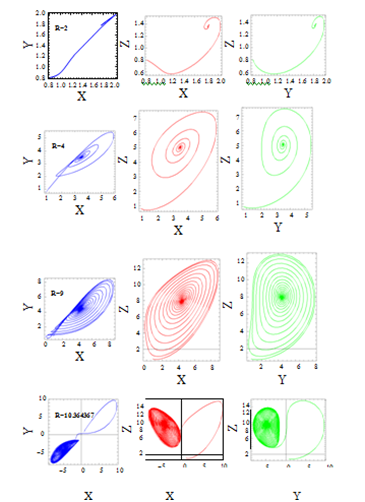
Figure 2 Phase portraits for evolution of trajectories over time in the state space for different values (R) Ω₁= 0.245, δ₁=0.02, R_i=0.1, Pr=10, A=0.6, Γ=0.3.

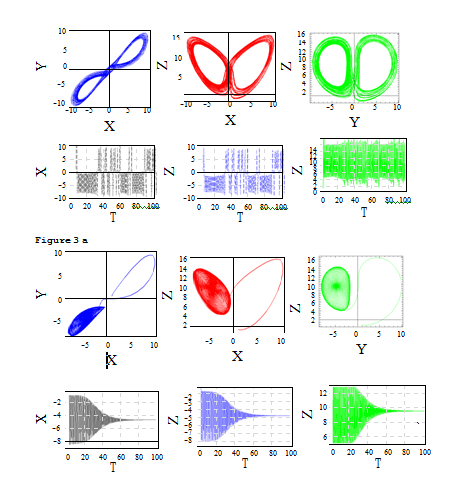
Figure 3 Phase portraits for evolution of trajectories over time in the state space: The amplitude solution in the time domain for Ω₁=0.245, δ₁=0.02, R=10.364367, R_i=0.4223, A=0.6, Γ= 0.3 b:Projections and evolution of trajectories over the planes X-Y,Y-Z,Z-X and a time domain of solutions for Ω₁=0.245, δ₁=0.0, R_i=0.4223, A=0.6, Γ=0.3(Ω₂=0, δ₂=0.02).

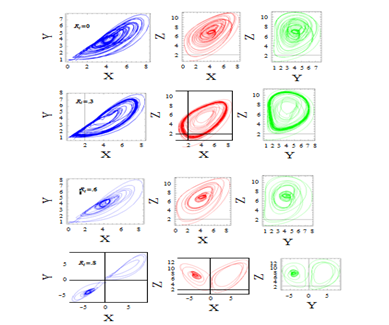
Figure 4 Projections and evolution of trajectories over the planes X-Y Y-Z Z-X for Ω₁=10, δ₁=0.3, R=8, A=0.6, Γ=0.3.

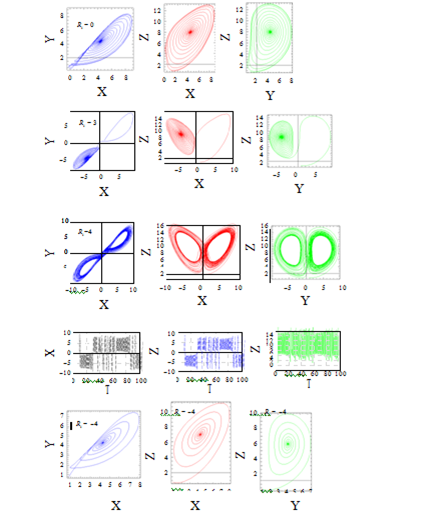
Figure 5 Projections and evolutions of trajectories over the planes X-Y,Y-Z,Z-X and a time domain of solutions for φ=π, Ω₁=0, δ₁=0, R=9, A=0.6, Γ=0.3.

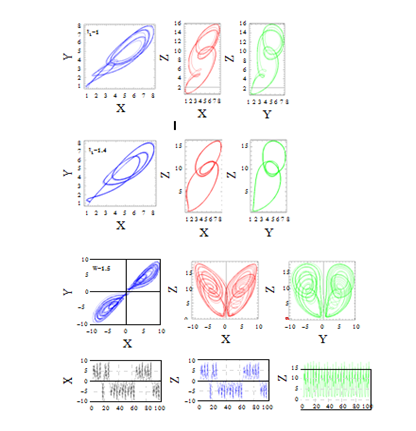
Figure 6 Projections and evolution of trajectories over the planes X-Y Y-Z Z-X and a time domain of solutions for δ₁=1.5, R_i=0.1, R=8, A=0.6, Γ=0.3.

The effect of the ratio of retardation to relaxation times for Λ=2, the chaotic behavior becomes particularly obvious from the phase portrait and in time domain given in Figure 7. The effect of Λ is of similar results for unmodulated case obtained by Sheu et al.²⁰ The comparison among three types of thermal modulation is similar to the results of Kiran et al.³⁹ The results corresponding to gravity modulation is presented in Figures 8-11. All solutions were obtained using the same initial conditions which were used for thermal modulation, selected to be in the neighborhood of the positive convection fixed point, i.e., at τ=0 : X=Y=Z=0.9, W=0.1. In Figure 8 for corresponding set of parameter values (Ω₂=0.2, δ₂=0.01, R=14.496324567), where the system loses its stability at R_i=0 (non internal heating case). Which means for gravity modulation R=14.496324567 is the critical Rayleigh number where the solution of the corresponding system loses its stability. As varying the values of R_i positively, the transition to chaotic solution occurs at R_i=0.5 given in Fig. 9. For gravity modulated system, for lower values of amplitude and frequency of modulation, internal heating effect has a good influence on the dynamic of the system. For the set of values Ω₂=10, δ₂=0.1, R_i=0.0, and R=14.496324567, where the effect of frequency of modulation for low amplitude and non-internal heating system is observed in Figure 10, and found the chaotic behaviour of the solutions of the system. The effect of frequency of gravity modulation extensively analyzed by Vadasz et al.,³² and Bhadauria et al.,³⁸ the present results conforms their results. Consider the Darcy-Rayleigh number R<R_c=9.496324567 in order to reduce the effect of R on the solution of the system. For the values of Ω₂=0.15, δ₂=1, R_i=0.1 the solutions exhibit suddenly a typical chaotic behaviour around the two fixed points (figures represent the projection of the solution data points onto the corresponding planes), the amplitude solutions exhibit the chaotic behaviour in the time domain given in Figure 11.

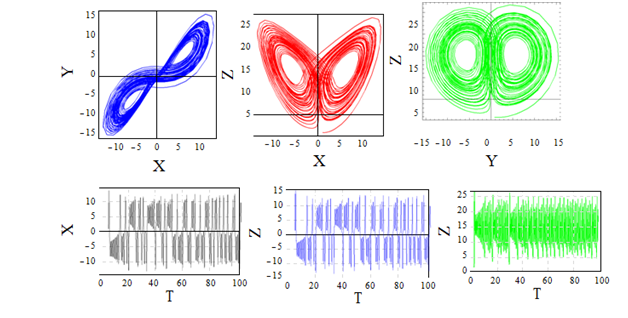
Figure 7 Projections of trajectories over the planes X-Y Y-Z Z-X and a time domain of solutions for Ω₁=0.243, δ₁=0.02, R_i=0.1, R=10.423452, A=0.2, Γ=0.3.

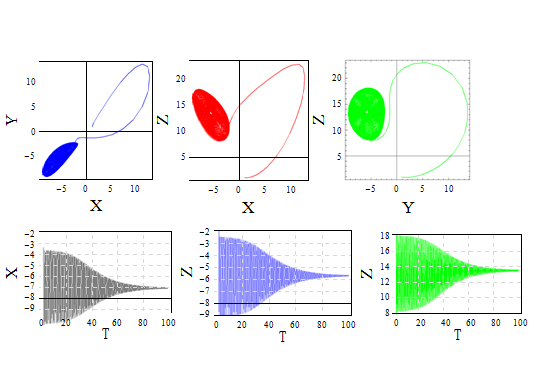
Figure 8 Projections of trajectories over the planes X-Y Y-Z Z-X and a time domain of solutions for Ω₂=0.2, δ₂=0.01, R_i=0.0, R = 14.496324567, A=0.7, Γ=0.2.

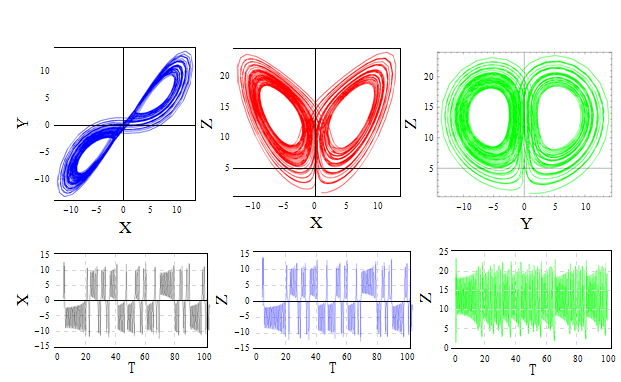
Figure 9 Projections of trajectories over the planes X-Y Y-Z Z-X and a time domain of solutions for Ω₂= 0.2, δ₂=0.01, R_i=0.5, R=14.496324567, A=0.7, Γ=0.2.

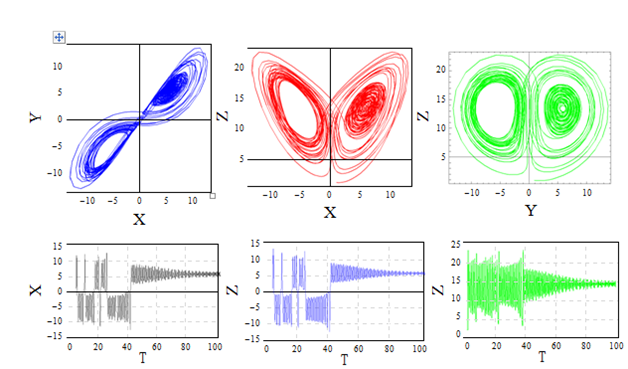
Figure 10 Projections of trajectories over the planes X-Y Y-Z Z-X and a time domain of solutions for Ω₂= 10, δ₂=0.1, R_i=0.1, R=14.496324567, A=0.7, Γ=0.2.

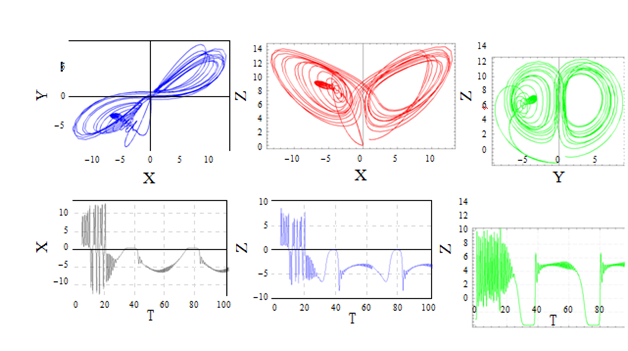
Figure 11 Projections of trajectories over the planes X-Y Y-Z Z-X and a time domain of solutions for Ω₂=0.15, δ₂=1, R_i=0.0, R=9.496324567, A=0.7, Γ=0.2.

Hence it is observed that, the amplitude of gravity modulation also play a critical role on the dynamic of the problem as δ₂ varies along with Ω₂, the transition from steady state solution moved to chaotic nature. The heat transfer results of the system presented in Figure 12A. The effect of internal Rayleigh Darcy number R_i, as usual, and it is found to enhance the heat transfer in the system. Similarly the modulation effect as followed by Venezian,⁴⁰ and Bhadauria et al.,^41‒43 where amplitude of modulation enhances (Figure 12B) the heat transfer and frequency of modulation is to diminish (Figure 12C) the heat transfer. The comparison among three types of temperature modulation is presented in Figure 12D, and conform the results of Bhadauria et al.,³⁸ and Kiran et al.³⁹ The dynamic of the problem for three types of temperature modulation is obtained from Kiran et al.³⁹ The comparison between modulated and unmodulated system is presented in Figure 12E. It is quite interest to see that, for temperature modulation the modulated case enhances the heat transfer than unmodulated case. The comparison between thermal and gravity modulation is presented in Figure 12E. It is found that, for gravity modulation these results are quite opposite given by Srivastava et al.,⁴⁸ where modulated flows transport less heat than their corresponding unmodulated flows conforms the results of Gresho et al.,³³ and Kiran et al.,³⁹ and Davis.⁴⁹ The following relation can generalize the heat transfer

Figure 12 Results of heat transfer Ω₂=1, δ₂=0.1, R_i=0.02, R=15, A=0.7, Γ=0.2.

$N{u}_{Tmp}mod>N{u}_{un-mod}>N{u}_{gvtymod}$     (7.1)

A study of nonlinear thermal convection in a porous medium with non-Newtonian fluid for two-dimensional spatial case is investigated, in particular derived a set of ordinary nonlinear differential equations, which describe as a minimal model for the complex dynamic behavior in the presence of internal heat source and under temperature and gravity modulations. Without modulation, and internal heat source a classical Lorenz model will be recovered. The parameter regions were obtained where the stationary states or those with chaotic or regular dynamics will occur under modulations.⁵⁰ while performing a numerical simulation using Mathematica8 and found that, the system has multiple transitions between regular and chaotic behavior under modulation and internal heat source. The following conclusions are drawn.

1. The effect of R_i, for heat source R_i>0 advances the chaotic nature of the system under modulation, opposite results i.e. steady state solutions obtained for heat sink R_i<0.
2. Taking the suitable ranges of Ω₁, δ₁ and R, the chaotic behaviour of the solution of the system is controlled.
3. Thermal modulation inhabits and gravity modulation delays the chaotic convection.
4. Heat transfer is more for temperature modulation than gravity modulation.
5. The results corresponding to gravity modulation may be compared with Vadasz et al.,³² for temperature modulation with Kiran et al.³⁹

The author Dr. Palle Kiran is grateful to the Department of Atomic Energy, Government of India, for providing him financial assistance in the form of NBHM-Post-doctoral Fellowship (Lett. No: 2/40(27)/2015/R&D-II/9470). The authors are grateful to the unknown referees for their useful comments that helped to refine the paper in its current form.

The author declares that there are no conflicts of interest.

1. Bhadauria S, Kiran P. Weakly nonlinear oscillatory convection in a viscoelastic fluid saturating porous medium under temperature modulation. Int J of Heat Mass Transf. 2014;77:843−851.
2. Bhadauria BS, Kiran P. Heat and mass transfer for oscillatory convection in a bi- nary viscoelastic fluid layer subjected to temperature modulation at the boundaries. Int Communi in Heat and Mass Transf. 2014;58:166−175.
3. Bhadauria BS, Kiran P. Weak nonlinear double diffusive magneto convection in a Newto- nian liquid under temperature modulation. Int J Eng Math. 2014;204:01−14.
4. Poincar´e JH. Les m´ethodesnouvelles de la m´echaniquec´eleste. Paris: Boston Public Library; 1892. 412 p.
5. Poincare JH. Les m´ethodesnouvelles de la m´echaniquec´eleste. Paris: Gauthier-Villars et fils; 1899. 429 p.
6. Poincar´e JH. Sur le probl´eme des trois corps et les´equations de la dynamique. Acta Mathematica. 1890;13:1–270.
7. Lorenz EN. Deterministic non-periodic flow. J Atmos Sci. 1963;20(2):130−148.
8. Ro¨ssler OE. An equation for continuious chaos. Phys Lett A. 1976;57(5):397−398.
9. Chen GR, Ueta T. Yet another chaotic attractor. Internat J Bifur Chaos. 1999;9(7):1465−1466.
10. Lu¨ JH, Chen GR. A new chaotic attractor conined. Int J Bifur Chaos. 2002;12(3):659−661
11. Adomian G. A review of the decomposition method in applied mathematics. J Math Anal Appl. 1988;135(2):501−544.
12. Adomian G. Solving frontier problems in physics: The decomposition method. Dordrecht: Kluwer Academic Publishers. 1994.
13. Vadasz P, Olek S. Transitions and chaos for free convection in a rotating porous layer. Int J of Heat and Mass Transf. 1998;41(11):1417−1435.
14. Vadasz P, Olek S. Weak turbulence and chaos for low Prandtl number gravity driven convection in porous media. Transp Porous Media. 1999;37(1):69−91.
15. Vadasz P. Local and global solutions for transitions to chaos and hysteresis in a porous layer heated from below. Transp Porous Media. 1999;37(2):213−245.
16. Sparrow C. The Lorenz Equations: Bifurcations, chaos and strange attractors. New York: Springer Verlag; 1982. p. 1–12.
17. Wang Y, Singer J, Bau HH. Controlling chaos in a thermal convection loop. J Fluid Mech. 1992;237:479–497.
18. Yuen P, Bau HH. Rendering a subcritical Hopf bifurcation supercritical. J Fluid Mech. 1996;317:91−109.
19. Feki M. An adaptive feedback control of linearizable chaotic systems. Chaos Solitons and Fractals. 2003;15(5):883−890.
20. Yau HT, Chen CL. Chaos control of Lorenz systems using adaptive controller with input saturation. Chaos Solitons Fractals. 2007;34(5):1567−1574.
21. Sheu LJ, Tam LM, Chen JH, et al. Chaotic convection of viscoelastic fluids in porous media. Chaos, Solitons and Fractals. 2008;37(1):113−124.
22. Yau HT, Chen CK, Chen CL. Sliding mode control of chaotic systems with uncertainties. Int J Bifurcation Chaos. 2000;10(5):1139−1147.
23. Peng CC, Chen Chaos CL. Robust chaotic control of Lorenz system by backstepping design. Solitons Fractals. 2008;37(2):598−608.
24. Vadasz P. Analytical prediction of the transition to chaos in Lorenz equations. Appl Math Lett. 2010;23(5):503−507.
25. Narayana M, Gaikwad SN, Sibanda P, et al. Double diffusive magneto-convection in viscoelastic fluids. Int J of Heat Mass Transf. 2013;67:194−201.
26. Narayana M, Sibanda P, Siddheshwar PG, et al. Linear and nonlinear stability analysis of binary viscoelastic fluid convection. Appl Math Model. 2013;37(16-17):8162−8178.
27. Hetsroni G, Gurevich M, Rozenblit R. Natural convection in metal foam strips with internal heat generation. Expe Thermal Fluid Science. 2008;32(8):1740−1747.
28. Saravanan S. Thermal non-Equilibrium porous convection with heat generation and den- sity maximum. Transp. Porous Media. 2009;76(1):35−43.
29. Bhadauria BS, Kumar A, Kumar J, et al. Natural convection in a rotating anisotropic porous layer with internal heat. Transp Porous Media. 2011;90:687−705.
30. Bhadauria BS. Double diffusive convection in a saturated anisotropic porous layer with internal heat source. Transp Porous Media. 2012;92(2):299−320.
31. Bhadauria BS, Hashim I, Siddheshwar PG. Study of heat transport in a porous medium under G-jitter and internal heating effects. Transp Porous Media. 2013;96(1):21−37.
32. Bhadauria BS, Hashim I, Siddheshwar PG. Effects of time-periodic thermal boundary conditions and internal heating on heat transport in a porous medium. Transp Porous Media. 2013;97(2):185−200.
33. Vadasz JJ, Meyer JP, Saneshan G. Chaotic and periodic natural convection for moderate and high Prandtl numbers in a porous layer subject to vibrations. Transp Porous Media. 2014;103(2):279−294.
34. Gresho PM, Sani RL. The effects of gravity modulation on the stability of a heated fluid layer. J Fluid Mech. 1970;40:783−806.
35. Bhadauria BS, Kiran P. Nonlinear thermal Darcy convection in a nanofluid saturated porous medium under gravity modulation. Advanced Science Letters. 2014;20:903−910.
36. Bhadauria BS, Kiran P. Nonlinear thermal convection in a layer of nanofluid under G- jitter and internal heating effects. MATEC-Web of Conferences. 2014;16:7.
37. Kiran P. Throughflow and g-jitter effects on binary fluid saturated porous medium. Applied Math Mech Accepted. 2015;36(10):1285–1304.
38. Kiran P. Nonlinear thermal convection in a viscoelactic nanofluid saturated porous medium under gravity modulation. Ain Shams Eng J. 2016;7(2):639–651.
39. Bhadauria BS, Kiran P. Chaotic and oscillatory magneto−convection in a binary vis- coelastic fluid under G-jitter. Int J of Heat Mass Transf. 2015;84:610−624.
40. Kiran P, Bhadauria BS. Chaotic convection in a porous medium under temperature mod- ulation. Transp Porous Media. 2015;107(3);745−763.
41. Venezian G. Effect of modulation on the onset of thermal convection. J Fluid Mech. 1969;35(2):243−254.
42. Bhadauria BS, Kiran P. Heat transport in an anisotropic porous medium saturated with variable viscosity liquid under temperature modulation. Transp Porous Media. 2013;100(2):279−295.
43. Kiran P. Throughflow and non-uniform heating effects on double diffusive oscillatory convection in a porous medium. Ain Shams Eng J. 2016;7(1):453–462.
44. Bhadauria BS, Kiran P. Effect of rotational speed modulation on heat transport in a fluid layer with temperature dependent viscosity and internal heat source. Ain Shams Eng J. 2014;5(4):1287−1297.
45. Kiran P, Bhadauria BS. Nonlinear throughow effects on thermally modulated porous medium. Ain Shams Eng J. 2015.
46. Vadasz P, Olek S. Route to chaos for moderate Prandtl number convection in a porous layer heated form below. Transp Porous Media. 2000;41(2):211−239.
47. Magyari E. The butterfly effect in a porous slab. Transp. Porous Media. 2010;84(3):711−715.
48. Vadasz P. Subcritical transitions to chaos and hysteresis in a fluid layer heated from below. Int J of Heat and Mass Transf. 1999;43(5):705−724.
49. Srivastava A, Bhadauria BS, Siddheshwar PG, et al. Heat transport in an anisotropic porous medium saturated with variable viscosity liquid under G-jitter and internal heating effects. Transp Porous Media. 2013;99(2):359−376.
50. Davis SH. The stability of time periodic flows. Annual Review of Fluid Mech. 1976;8:57−74.