Almost all catalytic reactions in the petrochemical industry are reversible and therefore their conversion is limited by the thermodynamic equilibrium. This conservative limitation can be broken by using selective membranes to remove one of the products. In this paper this revolutionary concept is used for the dehydrogenation reaction where the selective membranes are used for the perm-selective removal of hydrogen.^1–3 These membranes have 100% selectivity for the removal of hydrogen. Most efficient configuration is when in the other side of the membrane is a hydrogenation reaction and the flows in the two sides of the membrane are counter-current.

Most catalytic reactions are reversible and are therefore controlled by the thermodynamic equilibrium constant of the reaction limiting its conversion. The removal of one, or more , of the products relaxes this limitation and increases the conversion of the reaction, this relaxation increases as the removal of the product(s) is increased. This paper is concentrating on the removal of hydrogen from a dehydrogenation reaction, mainly ethyl-benzene to styrene (1-3), using a hydrogen perm-selective membrane. The rate of hydrogen removal from the reaction side depends upon the type of the membrane and also the hydrogen driving force between the two sides of the membranes. This driving force increases when there is a hydrogenation reaction in the other side of the membrane. In the present study a hydrogenation reaction of nitrobenzene to aniline is taking place on the other side of the membrane. A reliable mathematical model is used to investigate the characteristics of this novel membrane reactor configuration.

The reaction network for the dehydrogenation of ethyl-benzene to styrene is:^3–6

$C_6{H}_{5}C{H}_{2}C{H}_3\iff C_6{H}_{5}CHC{H}_2+H_2$ $\Delta H_{298}=117.6\frac{kJ}{mole}$ ……………… (1)
$C_6{H}_{5}C{H}_{2}C{H}_3\to C_6{H}_6+C_2{H}_4$ $\Delta H_{298}=105.4\frac{kJ}{mole}$ ………………. (2)
$C_6{H}_{5}C{H}_{2}C{H}_3+H_2\to C_6{H}_{5}C{H}_3+C{H}_4$ $\Delta H_{298}=-54.6\frac{kJ}{mole}$ ………………. (3)
$2H_{2}O+C_2{H}_4\to 2CO+4H_2$ $\Delta H_{298}=210.2\frac{kJ}{mole}$ ……………….. (4)
$H_{2}O+C{H}_4\to CO+3H_2$ $\Delta H_{298}=206.1\frac{kJ}{mole}$ ……………….. (5)
$H_{2}O+CO\to C{O}_2+H_2$ $\Delta H_{298}=-41.2\frac{kJ}{mole}$ ……………….. (6)

In this network, all side reactions are irreversible with the only reversible reaction being the main reaction which produces styrene. The corresponding rate equations, expressed as functions of component partial pressure in bars, are:^3–6

$r_1=k_1\left(p_{EB}-p_{ST}\frac{p_{H_2}}{K_A}\right)$ …………………. (7)
$r_2=k_2{p}_{EB}$ ......................... (8)
$r_3=k_3{p}_{EB}{p}_{H_2}$ ................................ (9)
$r_4=k_4{p}_{H_{2}O}{p}_{C_2{H}_4}^{1/2}$ ........................... (10)
$r_5=k_5{p}_{H_{2}O}{p}_{C{H}_4}$ ................................. (11)
$r_6=k_6\left(\frac{P}{T^3}\right)p_{H_{2}O}{p}_{CO}$ ........................... (12)

with rate constants defined as:

$k_i=\exp \left(A_i-\frac{E_i}{RT}\right)$ ……………. (13)

The numerical values of A_i and E_i given in Table 1 are used to calculate the rate of reactions in kmol/kg cat/h. To change the units of partial pressures from bars to Pascal and the reaction rates from kmol/kg cat/h to mol/kgcat/s, the above rate equations (1-6) have to be multiplied by the constants in Table 2. On the tube side, the hydrogenation reaction of nitrobenzene to aniline is given⁷ by:

$C_6{H}_{5}N{O}_2+3H_2\to C_6{H}_{5}N{H}_2+2H_{2}O$ $\Delta H_{298K}=-443.0\frac{kJ}{mole}$ ………….. (14)

The rate equation of this reaction is estimated⁷ by:

$r^{\prime }=\frac{k^{\prime }{K}_{NB}{K}_{H_2}{p^{\prime }}_{NB}\sqrt{{p^{\prime }}_{H_2}}}{{\left(1+K_{NB}{p^{\prime }}_{NB}+K_{H_2}\sqrt{{p^{\prime }}_{H_2}}\right)}^2}$ ……………………. (15)

with reaction rate constant defined as:

$k^{\prime }={10}^3\exp \left(A^{\prime }-\frac{E^{\prime }}{R{T}^{\prime }}\right)$ …………….. (16)

Figure 1 Schematic diagram showing integrated reactor configuration.

where:

A’=0.186, E’=10.0×10³ J/mole, ${\text{K}}_{{\text{H}}_{\text{2}}}=4.427\times {10}^{-3}{\text{Pa}}^{-\text{1/2}}$ , ${\text{K}}_{\text{NB}}=1.510\times {10}^{-5}{\text{Pa}}^{-\text{1}}$
(fig 1)

To obtain the mole balance equation and the energy balance equation, a differential element inside the membrane reactor was considered. After writing the two balances under the steady state assumption, both sides of the resulting equations were divided by the thickness of the differential element, which was then forced to approach zero. The resulting balances equations of the shell side can be expressed as:
Mole balance:

$\frac{d{n}_i}{dz}={\displaystyle {\sum }_{j=1}^6{\sigma }_{ij}{r}_j\left(1-\epsilon \right)}{A}_{cs}{\rho }_s-2\pi r_{3}N{a}_i{J}_i$
……………….. (17)

Energy balance:

$\frac{dT}{dz}=\frac{{\displaystyle {\sum }_{j=1}^6{\left[-\Delta H\left(T\right)\right]}_j}{r}_j\left(1-\epsilon \right)A_{cs}{\rho }_s+Q}{{\displaystyle {\sum }_{i=1}^{10}{n}_{i}C{p}_i}}$ ……………………. (18)

Pressure drop:

$\frac{dP}{dz}=-\frac{G}{{\rho }_g{g}_c{D}_p}\left(\frac{1-\epsilon }{{\epsilon }^3}\right)\left[\frac{150\left(1-\epsilon \right){\mu }_g}{D_p}+1.75G\right]$ ………………….. (19)

The corresponding balance equations for the tube side can be expressed as:
Mole balance:

$\frac{d{n^{\prime }}_i}{dz}={\left(-1\right)}^b\left[{\sigma }_i{r}^{\prime }\left(1-{\epsilon }^{\prime }\right){A^{\prime }}_{cs}{{\rho }^{\prime }}_s+2\pi r_3{a}_i{J}_i\right]$ ………………………… (20)

Energy balance:

$\frac{d{T}^{\prime }}{dz}={\left(-1\right)}^b\left[\frac{\left(2\pi r_3\right){\displaystyle {\sum }_{i=1}^i{a}_i{J}_i{\displaystyle \underset{T^{\prime }}{\overset{T}{\int }}C{p}_{i}dT+\left[-\Delta H^{\prime }\left(T^{\prime }\right)\right]r^{\prime }\left(1-{\epsilon }^{\prime }\right){A^{\prime }}_{cs}{{\rho }^{\prime }}_s-Q}}}{{\displaystyle {\sum }_{i=1}^4{n^{\prime }}_{i}C{p^{\prime }}_i}}\right]$ ………………… (21)

Pressure drop:

$\frac{d{P}^{\prime }}{dz}={\left(-1\right)}^b\frac{G^{\prime }}{{{\rho }^{\prime }}_g{g}_c{D^{\prime }}_p}\left(\frac{1-{\epsilon }^{\prime }}{{{\epsilon }^{\prime }}^3}\right)\left[\frac{150\left(1-{\epsilon }^{\prime }\right){{\mu }^{\prime }}_g}{{D^{\prime }}_p}+1.75G^{\prime }\right]$ …………. (22)

The hydrogen flux across the membrane surface obeys Sievert’s law,⁸ i.e.

$J_{H_2}=\frac{Q_o\exp \left(-\frac{E_{H_2,P}}{RT}\right)}{{\delta }_{H_2}}\left(\sqrt{P_{H_2}}-\sqrt{{P^{\prime }}_{H_2}}\right)$ ………………… (23)

The pre-exponential constant, permeation activation energy, and the thickness of the hydrogen permeation membrane are taken as 6.33×10^-7 mol/m/sec/Pa^0.5, 15700 J/mole, and 1~2×10^-5 m, respectively.⁸ Heat transfer across the membrane involves both convection from the gas mixture to the membrane, conduction across the membrane layer, and finally convection from the membrane to the second gas mixture. Radiation of heat is neglected. The membrane tube is considered to be a composite wall having a stainless steel layer coated by a thin layer of palladium. The thermal conductivities of the stainless steal layer and the palladium are taken to be 24.5 W/m×K and 93.3 W/m×K, average values over a temperature range of 200-1800 K.^9,10 The heat transferred per unit length from each tube is obtained from:

$Q=\frac{2\pi r_1\left(T^{\prime }-T\right)}{\left[\frac{1}{h^{\prime }}+\frac{r_1}{k_{ss}}\ln \left(\frac{r_2}{r_1}\right)+\frac{r_1}{k_{Pd}}\ln \left(\frac{r_3}{r_2}\right)+\frac{r_1}{r_{2}h}\right]}$ …………………. (24)

The convective heat transfer coefficients in equation (24) are calculated using Leva’s correlation (1949).¹¹ For the shell side in which the reacting mixture is heated up, the convective heat transfer coefficient is calculated by [11]:

$\frac{h{D}_t}{k_g}=0.813{\left(\frac{D_{p}G}{{\mu }_g}\right)}^{0.9}\exp \left(-\frac{6D_p}{D_t}\right)$ …………………… (25)

In contrast, the reacting mixture in the tube side is cooled and consequently the convective heat transfer coefficient is calculated by:¹¹

$\frac{h^{\prime }{D^{\prime }}_t}{{k^{\prime }}_g}=3.50{\left(\frac{{D^{\prime }}_p{G}^{\prime }}{{{\mu }^{\prime }}_g}\right)}^{0.7}\exp \left(-\frac{4.6{D^{\prime }}_p}{{D^{\prime }}_t}\right)$ ………………. (26)

Physical properties such as, thermal conductivity, gas density and viscosity, and heat capacities are taken as functions of temperature from Yaws.⁹

In the case of the co-current operation $\left(b=2\right)$ , the above system of differential equations gives an initial value problem which can be solved by a Runge-Kutta Verner fifth and sixth order method with an automatic step size, double precision calculation, and a relative error of 1×10^-12 to ensure high accuracy. The initial conditions are:
At: $z=0$                                

$ShellCompartment=\{\begin{array}{l}{n}_i=n_{if}\\ T=T_f\\ P=P_f\end{array}$ …………………. (27)

$TubeCompartment=\{\begin{array}{l}{n^{\prime }}_i={n^{\prime }}_{if}\\ T^{\prime }={T^{\prime }}_f\\ P^{\prime }={P^{\prime }}_f\end{array}$ ………………….. (28)

For the counter-current operation case $\left(b=1\right)$ , the above system of differential equations results in a split two-point boundary value problem which can be solved by an orthogonal collocation technique [12,13]. The boundary conditions are:

At $z=0$ inlet condition of dehydrogenation compartment

$ShellCompartment=\{\begin{array}{l}{n}_i=n_{if}\\ T=T_f\\ P=P_f\end{array}$ …………………. (29)

At $z=L$ inlet condition of hydrogenation compartment

$TubeCompartment=\{\begin{array}{l}{n^{\prime }}_i={n^{\prime }}_{if}\\ T^{\prime }={T^{\prime }}_f\\ P^{\prime }={P^{\prime }}_f\end{array}$ …………………….. (39)

The operating conditions for both sides of the reactor are given in Table 3 & Table 4. For the dehydrogenation reaction of ethyl-benzene to styrene, the feed molar flow rates are the same as those presented by Elnashaie et al.^4,6 whereas the molar flow rate of nitrobenzene is based on stoichiometry. Excess steam is provided in the feed line to prevent the formation of coke on the catalyst.

The simulation results for the coupled membrane reactor system can confirm the potential of coupling the two reactions. In general, the achievable performance as far as conversion of ethyl-benzene and yield of styrene are concerned is much better than that of the corresponding uncoupled industrial fixed bed reactors operated at the same conditions. The coupled membrane reactor also has the potential to give better conversion of ethyl-benzene and yield of styrene by increasing the length of the reactor since the two profiles continue to evolve with distance:

Hydrogen molar flow rate

Hydrogen molar flow rates for an uncoupled fixed bed reactor and for coupled co-current and countercurrent cases membrane reactors are shown in Figure 2. Hydrogen is generated in the uncoupled fixed bed reactor case while producing styrene, which is the key component, is low. For the coupled co-current case, on the other hand, hydrogen produced on the dehydrogenation side diffuses immediately through the membrane walls of the hydrogenation tubes where it meets nitrobenzene to react and produce aniline. The comparable rates of the net production of hydrogen on the dehydrogenation side and the rate of diffusion of hydrogen through the palladium membrane prevent the hydrogen from accumulating on the dehydrogenation side where it reduces the net reaction rate. The coupled countercurrent case is of special interest due to the presence of a maximum where the flow rate of hydrogen reaches a maximum and then decreases. At the feed end of the dehydrogenation side ( $z=0$ ), the rate of production of hydrogen by reactions (1), (4), (5), and (6) surpasses both the rate of consumption of hydrogen by reaction (3) and the rate of diffusion of hydrogen through the palladium membrane. This leads to an increase in the number of moles of hydrogen until a point is reached where the hydrogen flow rate has reached its maximum value, i.e. when the rate of change of molar flow rate of hydrogen at that point with respect to the length of the reactor is zero. At this point, the rate of the production of hydrogen is balanced by both the rate of consumption of hydrogen by reaction (3) and the rate of diffusion of hydrogen through the membrane. Beyond that point, the process is dominated by consumption of hydrogen by reaction (3) and diffusion of hydrogen through the membrane. Consequently, the molar flow rate of hydrogen decreases along the reactor. This trend induces similar behavior in the hydrogenation tubes. As nitrobenzene moves from its feed point, located at $\text{z}=\text{3}\text{.0}\text{m}$ , it reacts with the permeate hydrogen. Another maximum is reached where the rate of diffusion of hydrogen through the membrane is balanced by its rate of consumption by the hydrogenation reaction. This point is located to the left Figure 2 of that on the dehydrogenation side. After passing this maximum, the rate of consumption of hydrogen dominates causing the amount of hydrogen in the hydrogenation tubes to drop quickly.

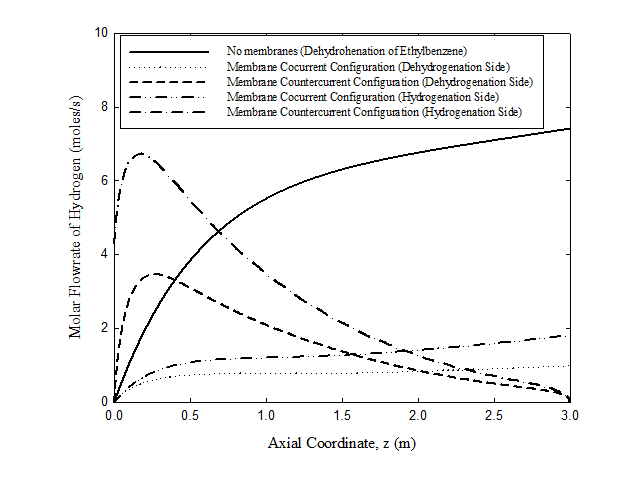
Figure 2 molar flow of hydrogen on uncoupled adiabatic fixed bed and coupled co-current and countercurrent cases of the novel membrane reactor. For operating conditions see Tables 3 & 4. For counter-current case, feed is from the right for the hydrogenation compartment; otherwise all feeds are from the left.

Conversion of ethyl-benzene

The predicted conversion of ethyl-benzene on the dehydrogenation side is shown in Figure 3 for the same three cases. For the operating conditions chosen, the conversion reaches 23.4% for the uncoupled adiabatic fixed bed case, 54.6% for the membrane reactor with co-current flow, and 61.7% for the membrane reactor in the countercurrent flow configuration. Again, coupling of the two reactions has the potential to provide significant improvement in reactor performance. Moreover, the heat generated by the exothermic hydrogenation reaction is put to good use, rather than being simply rejected to cooling water.

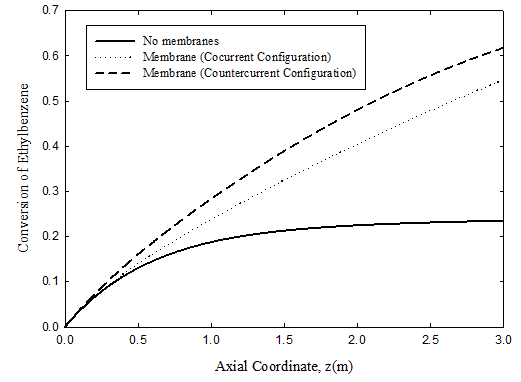
Figure 3 Comparison of ethyl-benzene conversions on dehydrogenation side for uncoupled adiabatic fixed bed and for coupled co-current and counter-current cases. For operating condition, see Tables 3 & 4.

Yield of styrene

Three cases are investigated: uncoupled fixed bed case corresponding to the classical industrial operation, co-current coupled case, and countercurrent coupled case. Results for the three cases are shown in Figure 4. The lowest yield by a considerable margin is predicted for the uncoupled adiabatic fixed bed where the maximum yield is 18.9%. For the membrane reactor, the predicted yield increases to 52.5% for the co-current flow configuration and 57.7% for the counter-current case.

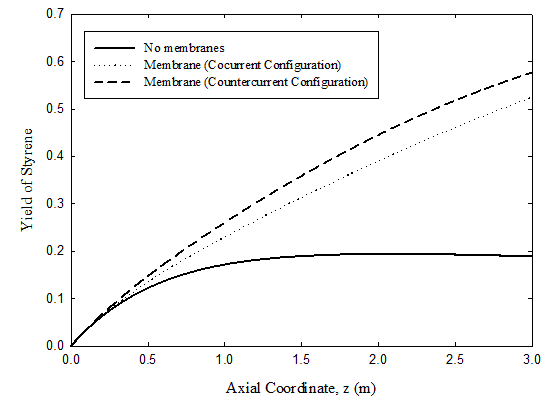
Figure 4 Comparison of styrene yields on dehydrogenation side for uncoupled adiabatic fixed bed and for coupled co-current and counter-current cases. For operating condition, see Tables 3 & 4.

Conversion of nitrobenzene

Figure 5 plots the predicted conversion of nitrobenzene as a function of distance along the reactor for the hydrogenation reaction to aniline. The counter-current membrane reactor is seen to give higher conversion than the co-current case because of the large driving forces. The conversion for the co-current case is predicted to reach 51.1%, while 57.9% is calculated for the counter-current case.

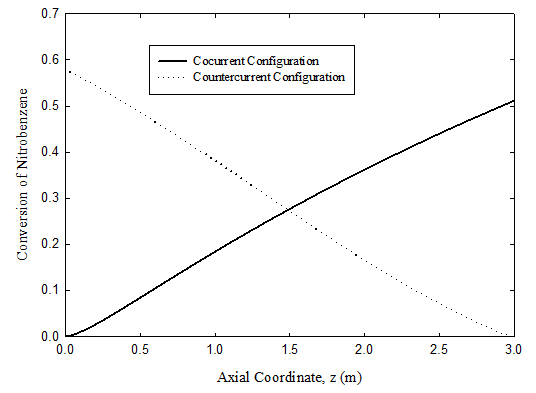
Figure 5 Conversion of nitrobenzene on the hydrogenation side for the co-current, and counter-current membrane reactor configurations. For operating conditions, see Tables 3 & 4.

Temperature profiles

Temperature profiles for the adiabatic fixed bed reactor and both the co-current and countercurrent membrane reactors are plotted in Figure 6 & 7 for different number of membrane tubes. Heat is continuously supplied from the exothermic hydrogenation nitrobenzene-to-aniline reaction on the tube side to the endothermic dehydrogenation reaction of ethyl-benzene on the shell side. The temperature variation is larger at the inlet of the membrane reactor in the coupled counter-current case than for coupled co-current flow. The fall in temperature for both cases of the coupled membrane reactor is much less than that for the uncoupled fixed bed reactor. In the counter-current case of the coupled reactor, the temperature on the dehydrogenation side drops because the heat transferred from the nitrobenzene side is decreased due to the low driving force, i.e. temperatures on both sides becomes comparable.

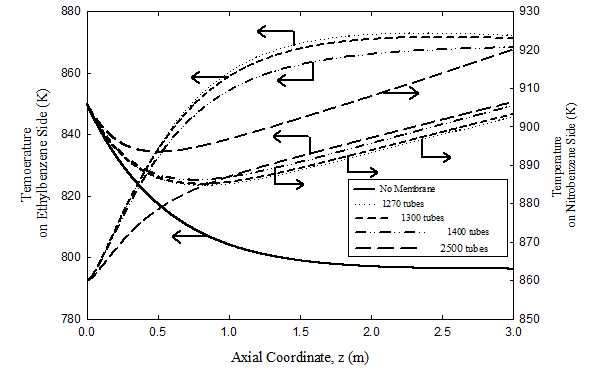
Figure 6 Effect of number of hydrogenation tubes on temperature profiles in the dehydrogenation and hydrogenation compartments for the co-current case. For operating conditions see Tables 3 & 4.

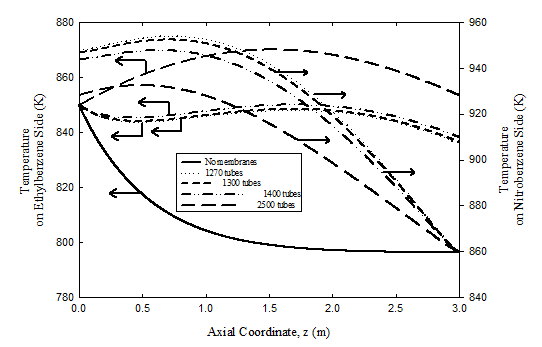
Figure 7 Effect of number of hydrogenation tubes on temperature profiles in the dehydrogenation and hydrogenation compartments for the coupled counter-current case. For operating conditions see Table 3 & 4.

Predicted temperature profiles on the hydrogenation side where the nitrobenzene to aniline reaction occurs are also plotted Figure 6 & 7 for different number of membrane tubes. The temperature rises from 860 K at the feed point to slightly more than 920 K for the coupled co-current flow case and slightly more than 945 K for the coupled counter-current flow configuration. The large temperature rise for the coupled counter-current coupled case is due to the large driving force causing higher diffusion rate of hydrogen and consequently increasing the nitrobenzene conversion. However, the temperature reaches a peak where both heat generated on the nitrobenzene side due to the reaction and energy carried by the permeating hydrogen is balanced by heat transfer through the membrane to the ethyl-benzene side. Later, it decreases because of the dominance of the heat transferred through the membrane.

Practical considerations

Coupling the exothermic hydrogenation reaction with the endothermic dehydrogenation reaction is predicted to be capable of providing a significant improvement in reactor performance and energy integration. However, it must be noted that palladium membranes are currently limited to temperatures of ~ 900 K. The maximum temperature can be reduced by increasing the number of the membranes, giving more surface area permitting more heat transfer rate across the membrane. This is illustrated in Figure 6 & 7 where the axial temperature profiles in both compartments of the coupled membrane reactor are plotted with flow rate kept unaltered. Note that the maximum temperature can be maintained below 880 K, with countercurrent operation giving higher maximum temperature than the co-current case. We also note that the counter-current configuration is likely to be very difficult to start up in practice. Hence, co-current operation Process control and safety aspects are also expected to be easier to provide for the co-current configuration despite the advantages of counter-current operation, which is more likely to be practical for the foreseeable future. Finally, while homogeneous one-dimensional models, like that used here, provide a good initial sense of what could be achieved in coupled fixed bed reactors, more comprehensive heterogeneous models with fewer simplifying assumptions are needed prior to proof-of-concept experiments on such reactors.

The performance of a newly configured membrane reactor with two reactions, an exothermic hydrogenation and an endothermic dehydrogenation reaction in parallel, has been modeled and evaluated for: co-current and counter-current operation. Pseudo homogeneous models have been used to describe the behavior of the system. In the range of the parameters used to investigate the performance of the membrane reactor, the simulation predicts a considerable increase in the conversion of ethyl-benzene and yield of styrene when the dehydrogenation reaction of ethyl-benzene to styrene is coupled with the hydrogenation reaction of nitrobenzene. The results from the counter-current mode of operation were in all cases higher than those from the co-current mode of operation due to the large driving forces. The simulation results suggest that coupling may be feasible in this case with promising performance. However, the performance of the reactor needs to be proven experimentally and tested over a range of parameters under practical operating conditions.

ai:                   Constant, 1 for hydrogen, 0 otherwise, [-]
Acs, A’cs: Cross sectional area of shell and tube side, [m2]
b: Constant, 2 for co-current, 1 for counter-current flow,[-]
Cpi, Cp’i: Heat capacity of component i on shell and tube side, $\left[\frac{J}{mole\times K}\right]$
Dp, D’p: Diameter of catalyst particle on shell and tube side, [m]
Dt:           Diameter of tube, [m]
Ej:            Activation energy of reaction j on shell side, $\left[\frac{J}{mole\times K}\right]$
E’:            Activation energy of the hydrogenation reaction on tube side, $\left[\frac{J}{mole\times K}\right]$
Hi, H’i:     Enthalpy of component i on shell and tube side, $\left[\frac{J}{mole}\right]$
L:  Total length of reactor, [m].
N:            Number of tubes in hybrid reactor, [-]
ni, n’I:      Molar flow rate of component i on shell and tube side, $\left[\frac{mole}{s}\right]$
Ji:             Molar flux of component i, $\left[\frac{mole}{m^2\times s}\right]$
pi, p’i:      Partial pressure of component i on shell and tube side, [Pa]
P:             Total pressure on shell side of reactor, [Pa]
P’:            Total pressure on tube side of reactor, [Pa]
Q:            Heat transferred from tube side to shell side, $\left[\frac{J}{m}\right]$
Qo:           Pre-exponential constant of the hydrogen membrane, $\left[\frac{mole}{m\times s\times P{a}^{0.5}}\right]$
rj:             Rate of reaction j on shell side, $\left[\frac{mole}{kgcat\times s}\right]$
r’:            Rate of reaction on tube side, $\left[\frac{mole}{kgcat\times s}\right]$
r1:            Inner radius of the hydrogenation tube, [m]
r2:            Outer radius of the hydrogenation tube, [m]
r3-r2:        Thickness of palladium membrane, [m]
T, T’:       Temperature on shell and tube side of reactor, [K]
Z:             Axial coordinate inside reactor, [m].
${\left[\Delta H\left(T\right)\right]}_j$ : Heat of reaction j at temperature T on shell side, [J/mole].
$\left[\Delta H^{\prime }\left(T^{\prime }\right)\right]$ Heat of reaction at temperature T’ on tube side, [J/mole].
Δz:          Thickness of differential element, [m]
ρs, ρ’s: Catalyst solid density on shell and tube side, $\left[\frac{kg}{m^3}\right]$
σij:           Stoichiometric coefficient of reactant i in reaction j, [-]
${\text{δ}}_{{\text{H}}_{\text{2}}}$ :       Thickness of hydrogen permeation membrane, [m]

None.

The author declares no conflict of interest.

1. Y She, J Han, YH Ma. Palladium membrane reactor for the dehydrogenation of ethylbenzene to styrene. Catal Today. 2001;67(1-3):43–53.
2. Ch Hermann, P Quicker, R Dittmeyer. Mathematical simulation of catalytic dehydrogenation of ethylbenzene to styrene in a composite palladium membrane reactor. J Membr Sci. 1997;136:161.
3. MEE Abashar. Coupling of ethylbenzene dehydrogenation and benzene hydrogenation reactions in fixed bed catalytic reactors. Chem Eng Pro. 2003;43:1195–1202.
4. TM Moustafa, SSEH Elnashaie. Simultaneous production of styrene and cyclohexane in an integrated membrane reactor. J Membr Sci. 2000;178:171.
5. SSEH Elnashaie, T Moustafa, T Alsoudani, et al. Modeling and basic characteristics of novel integrated dehydrogenation-hydrogenation membrane catalytic reactors. Com Chem Eng. 2000;24:1293–1300.
6. Abdulla BK, Elnashaie SSHE. A membrane reactor for the production of styrene from ethylbenzene. J Membr Sci. 1993;85:229.
7. B Amon, H Redlingshofer, E Klemm, et al. Kinetic investigation of deactivation by coking of a noble metal catalyst in the catalytic hydrogenation of nitrobenzene using a catalytic wall reactor. Chem Eng Pro. 1999;38:395.
8. Shu BPA, Grandjean S, Kaliaguine. Methane steam reforming in symmetric Pd-and Pd-Ag/porous SS membrane reactor. Appl Catal. 1994;119:305–325.
9. Carl Yaws. Chemical Properties Handbook: Physical, Thermodynamics, Engironmental Transport, Safety & Health Related Properties for Organic & Inorganic Chemical. New York: McGraw-Hill; 1999.
10. Suttichai Assabumrungrat, Kobkan Suksomboon, Piyasan Praserthdam, et al. Simulation of a Palladium Membrane Reactor for Dehydrogenation of Ethylbenzene. J Chem Eng Jpn. 2002;35:263.
11. Gilbert Froment, Kenneth Bischoff. Chemical Reactor Analysis and Design. 2nd ed.USA: John Wiley and Sons; 1990.
12. J Valladsen, Michelsen ML. Solution of Differential Equation Models by Polynomial Approximation. New Jersey, USA, 1978. 446 p.
13. Lloyd N Trefethen. Spectral Methods in MATLAB, Society for Industrial and Applied Mathematics, Philadelphia. USA, 2000.