The results of studies of the process of hydrated alumina homogeneous precipitation were presented in this work. The variants of this process are considered. The most convenient embodiment of this process is the precipitation of hydrated alumina from its salts with the use of auxiliary substances, such as urea. Urea hydrolysis allows a homogeneous precipitation process under the most mild conditions. It is shown that the process of hydrolytic precipitation in the aluminum salt-urea system proceeds according to the dissociative mechanism S_N1. This article analyzes the regularities of precipitation of solid colloidal particles of hydrated metal oxides on the surface of various substrates. Two models of this process are proposed. The proposed α-model is a process of continuous nucleation of interaction centers, at random points of a free surface throughout the process. The proposed β-model provides for the instantaneous nucleation of these centers when they are randomly distributed over the entire surface of the substrate. Based on the proposed models, the average values of the following values are calculated: the thickness of the gel film; its roughness and specific surface area. The calculations carried out in the article showed that these parameters are universal functions of the degree of filling of the surface and do not depend on the specific model of the mechanism of the process. Studies have been conducted on the use of homogeneously precipitated aluminum hydroxide as a binder in the preparation of porous materials. The resulting materials have a developed specific surface area and porosity.

Keywords: simulation, homogeneous precipitation, thin films, hydrated alumina, urea, sorbents, catalysts, carrier for catalysts, heat-resistant composites

The development of methods for obtaining a large class of heat-resistant composite materials is based, first, on the use of new inorganic binders. Binding systems include compositions with wettable fillers, adhesion to fillers, capable of spontaneous condensation, curing, spontaneously or under the influence of external conditions: heating, changing pH, interaction with the hardener, etc. Gluing or monolitization in the material powder, lumpy or fibrous substances, the material, in the manufacturing process, can be shaped into a finished product using methods of casting, pressing, plastic molding. A large number of various inorganic binders are known. Most of them occupy an intermediate position between true and colloidal solutions, more closely approaching colloidal solutions.¹ The most famous is the silica sol.² However, it has a number of disadvantages. In addition, it is very difficult to obtain silica, in which there are no impurities of alkali metals. In this regard, great opportunities are opened by using an alumina sol.^3?5 The colloidal solution of hydrated alumina (alumina sol), in its behavior during the production of composite materials and in some of its physicochemical properties, differs little from silica sol. The technology for producing materials based on it practically does not differ from the technology of obtaining composites based on silica sol. In this case, the use of an alumina sol as a binder has a number of significant advantages. First, the composition is enriched in aluminum oxide, thereby increasing the heat resistance of the material. Secondly, the materials are more durable than with a silica sol binder distribution and the volume of the sample is more evenly. Thirdly, the use of alumina sol virtually eliminates its waste, since the gel on its basis undergoes further peptization and can again be used as a binder.¹ However, the colloidal solution of hydrated alumina also has certain differences from the silica sol. These differences are, first, in the mechanism of controlling the gelation process. If the silica sol in case one of the important factors gelation process is its pH, then for alumina sol such a factor is the ratio of the amounts of anion to aluminum. This ratio is regulated by the addition of hydrochloric or nitric acid. The use of alumina sol as a binder is one of the most promising directions in the field of creating refractory composite materials. There are various methods for producing hydrated oxides and colloidal solutions. These methods based on precipitation are of interest because precipitation produces hydrated oxides having the greatest surface activity. The precipitation of the hydrated oxides can be carried out in various ways. For example, precipitation from a homogeneous medium; precipitation at variable and constant pH; batch and continuous deposition.⁶ Among these methods, it highlights the homogeneous precipitation method. This is because this method ensures the simultaneous formation of nuclei of the solid phase evenly throughout the volume of the reaction vessel. The resulting particles of the solid phase have a narrow size distribution and maximum activity. In the case of the presence of substrates in the system, they act as some centers of crystallization or coagulation, the formation of active coatings on their surfaces. These processes are especially active in the contact zone of the filler particles in the composite materials, which leads to their additional gluing. Thus, various active sorbents^7,8 carrier for catalysts in the petrochemical industry^9,10 and refractory heat-shielding composite materials.^2,11?16 Homogeneous chemical deposition methods are an embodiment of sol-gel synthesis processes and are used to produce various highly disperse compounds. The method is based on the hydrolysis reaction of the basic and auxiliary substances. For these methods to obtain hydrated oxides are characterized by the following feature. When mixing the solution containing the precipitated substance and the reagent that is used as the base, precipitation does not occur, the system remains homogeneous. The formation of a precipitate is possible when, under the influence of some factor, the reagent-base begins to change its chemical composition due to solvolysis and other chemical reactions. The presence in the reaction medium of a certain substrate having a surface with specific properties, leads primarily to the interaction of the solid particles with the surface of the substrate and as a consequence, to their deposition on the surface.^17,18 Because the sol-gel process of formation of thin films with homogeneous precipitation of hydrated oxide particles on the substrate surface finds application in various technological processes, in this paper we attempted to simulate it.

There are various methods for producing aluminum hydroxide; methods based on precipitation are of interest because precipitation produces aluminum hydroxide having the greatest surface activity. Precipitation can be made: from a homogeneous medium; at variable and constant pH, in the periodic and continuous modes.⁶ Homogeneous chemical depositions methods are used to produce highly disperse compounds. The method is based on the hydrolysis reaction of the basic and auxiliary substances. These methods are characterized by the following - when mixing a solution containing a precipitated substance and a reagent that is used as a base, precipitation does not occur, the system remains homogeneous. Precipitation and precipitation are possible when, under the influence of a factor, the reagent-base begins to change its chemical composition, because of which precipitation begins. The following variants of homogeneous precipitation¹⁹:

1. Deep hydrolysis of the main component, resulting in the formation of hydrolysis products
2. Hydrolysis of an auxiliary component, which is an alkaline agent.

Preparation of Al(OH)₃ by the method of agitation

Essence of the method: a dilute solution of an aluminum salt is stirred for a long time, with hydrolysis and formation of hydrolysis products. The final product of hydrolysis is Al(OH)₃. Most often used sodium aluminate (alkaline solution, the concentration of OH-groups is quite high). From the inner coordination sphere, water molecules are displaced due to the hydrolysis of aluminum ions and a number of complexes are formed, with the formation of a solid phase.

Precipitation of hydrated alumina of its salts using auxiliary substances

If the system Al(NO₃)₃+?O(NH₂)₂ heated, the urea decomposes to ??₂ and NH₄OH (urea hydrolysis proceeds slowly even when heated 90-95^o?). A base is formed in the system and, consequently, the concentration of OH-groups in the system increases, which results in the hydrolysis of the salt Al(NO₃)₃. The higher the concentration of OH-groups, the greater the rate and, consequently, the degree of hydrolysis. Because of hydrolysis, ligands are displaced from the inner coordination sphere and OH groups are formed. The basis is the formation of monomeric complex compounds. Monomers are combined in dimers, then into trimers, etc., and then a solid phase is formed.²⁰ This method of preparation is called the sol-gel method. It is the basis of obtaining nanomaterials, i.e. the resulting compounds have a nano size. The homogeneous deposition method is used to remove impurities in solutions. Introduce reagents, in the presence of which catalytic polymerization of metals or metal ions, which are an impurity, takes place. This method has the following advantages:

1. There are no local super saturations in the system, since the resulting alkaline reagent is uniformly distributed throughout the volume, and therefore the formation of a new solid phase occurs simultaneously in the entire volume. Consequently, if there are no local super saturations and a solid phase is formed in the entire volume, it has the same chemical composition at each point of the reaction space and the same phase composition.
2. With this precipitation, a significant super saturation in the system is not achieved and, consequently, globules of approximately the same size are formed. Thus, by controlling the sol-gel transition process, it is possible to achieve a precipitate with approximately the same particle size (monodisperse particles).

Disadvantages:

1. This process can only be periodic and, consequently, inefficient (applies only to small-scale production).
2. The resulting solid phase has a low rate of filtration and washing.

The method of precipitation from a homogeneous medium is based on a bed precipitation of the precipitant upon the decomposition of a substance directly in the volume of the solution containing the precipitated reagent. Widely used methods of synthesis of precipitation in the interaction of the starting materials with ammonia, released in a homogeneous environment during the decomposition of urea. At room temperature, urea does not hydrolyze, so aluminum hydroxide does not form, and the medium remains homogeneous. When heated to a temperature above 70°, hydrolysis of urea takes place, because of which NH₃, CO₂, and OH^- molecules appear in the solution, the pH gradually increases and it becomes possible to form a precipitate. Because the release of ammonia NH₃ and ions OH^- occurs uniformly throughout the volume of the solution and its rate is regulated, it becomes possible to avoid local super saturations and, consequently, the inhomogeneity of the precipitate.

The study of the mechanism of homogeneous precipitation of hydrated alumina

Advantages of using urea as a precipitant – obtaining, dense, well-filtered and easily washable sediment. When precipitating from a homogeneous solution, less sorption of foreign ions by the formed hydrated oxide is observed than when it is precipitated with ammonia. The disadvantage of the method is a long duration of precipitation (1.5÷2 h). Precipitation is best carried out from solutions of sulfates or in the presence of salts of organic acids. Precipitation from solutions of nitrates or chlorides gives less satisfactory results.¹³ With homogeneous precipitation, in addition to precipitation in the solution volume, metal hydroxides and oxyhydrates can precipitate on the surface of various substrates, creating a thin layer of hydroxide gel. The method of precipitation of metal hydroxides on substrates has found application for the production of thin-layer inorganic sorbents and some composite materials.^21?23 We studied the process of hydrolytic precipitation of aluminum hydroxide. This is a complex process of nucleophilic substitution; it can proceed through two mechanisms: associative (S_N2) and dissociative (S_N1). For the S_N2 mechanism, the rate-determining step is a bimolecular reaction in which another replaces one nucleophilic reagent. Mechanism S_N1 is characterized by a two-step mechanism, in which the first step is slow monomolecular hydrolytic dissociation, followed by a rapid coordination reaction with the second reagent. The process of hydrolytic deposition usually proceeds through the dissociative mechanism S_N1. Therefore, the most convenient is the pH-metric study of the hydrolysis process, which was carried out in a thermostated cell at various temperatures using an ionomer as a pH monitor and the ionic strength of the solution. The results of the studies on the joint hydrolysis of aluminum chloride and urea are shown in Figure 1. This process is rather complex, multistage. The most important factor determining the rate of hydrolysis is the temperature, which not only determines the speed of the process, but also to some extent changes its stepwise mechanism. At the first station, the soil of the basic aluminum salts is formed. In the second stage, further hydrolysis of the basic aluminum salts is observed to form the desired product, the hydrated alumina gel. By adjusting the temperature, the concentration of the reagents, it is possible to influence the rate of formation of the aluminum hydroxide sol used as a binder. The centrifugation method using the analytical centrifuge TH-21 was as follows. The mixed solutions of aluminum and urea salts were thermostated in round-bottomed flasks with a reflux condenser. After some time, samples of the solution were taken, which were filled with capillaries 1mm in diameter. The capillaries were isolated from one side with mastic and centrifuged at a speed of 12,000rpm for 7.5min. Using a special measuring line, the relative height of the column of the precipitate was determined, over which the volume of the separated solid phase. Figure 2 shows the dependence of the relative amount of gel formed during the joint hydrolysis of an aluminum salt and urea on time. The formation of the gel depends on the concentration of the reagents, it occurs spontaneously in a very short period in the entire volume of the solution, and its quantity does not change with further heating. To determine the nature of the interaction of the aluminum salt with alkaline agents, experiments were conducted on potentiometric titration of the aluminum salt with solutions of ammonia and sodium hydroxide in the presence of various amounts of ammonium chloride and urea. The titration curves are shown in Figure 3. The presence of ammonium salts in the solution causes the appearance of a significant buffering of the system, a decrease in the final pH of the solution. When titrating with sodium hydroxide solution, the process proceeds to the formation of sodium aluminate, titration with a solution of ammonia produces a precipitate of hydrated alumina. Addition of ammonium salts shifts the equilibrium of the hydrolysis reaction towards the formation of aluminum hydroxide. The presence of urea virtually does not affect the course of the deposition process. To determine the uniformity of the formed sediment, the laser radiation scattering method was used. For these purposes, a special installation was created that allows the capillary to be scanned through a focused beam.²³ The installation scheme is shown in Figure 4. To ensure scanning of the test sample strictly along the axis of the capillary, a special attachment has been developed that allows the capillary to move along an axis perpendicular to the incident laser beam. Uniform translational movement of the capillary is carried out by means of a synchronous electric motor with gear transmission. The device for measuring laser scattering is mounted based on a photopolarimeter. The scattering intensity was determined by means of a photocell located at an angle of 45° to the laser beam. The capillary was scanned at a constant rate, and the scattering intensity was recorded automatically. The reliability of the results of measuring laser scattering is ensured with uniformity of the instrument system:

Where d_l - is the diameter of the laser beam; d_k - is the diameter of the capillary.

Figure 1 Kinetic curves of joint hydrolysis 1 M CO(NH₂)₂ and 0,1 M AlCl₃.

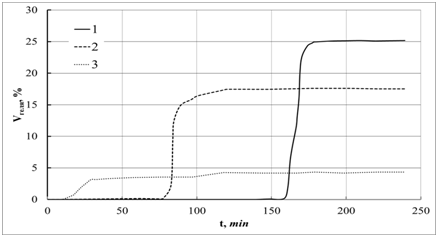
Figure 2 Deposition curves of the solid phase of the gel Al(OH)₃. The concentration of urea is C_CO(NH2)2= 1M. The concentration of aluminum chloride, corresponding to different curves, is: 1-0,1 ?; 2- 0,05 ?; 3-0,01 M

Figure 3 Limit values of pH by potentiometric titration of 0.1N solution of aluminum chloride with 0.1M solutions of NaOH (curves 1, 3) and NH₄OH (curves 2, 4) depending on urea concentration (curves 1, 2) and ammonium chloride curves 3, 4).

Figure 4 Installation for studying the scattering of laser radiation on capillaries with sediment: 1, He-Ne laser with wavelength ? = 600 nm; 2, focusing lens; 3, test sample with a device for moving along the axis; 4, photometric sensor; 5, amplifier; 6, recording unit.

To determine the homogeneity of the aluminum hydroxide structure formed by homogeneous precipitation, the solution samples the solution samples, after heat treatment, were placed in a glass capillary and centrifuged at a speed of 12,000rpm for 7.5min to precipitate and compact the hydrated alumina. In the capillaries after centrifugation, the scattering of laser radiation by scanning along the axis of the capillary was studied. A typical scattering curve is shown in Figure 5. From the data obtained, it can be seen that the solid phase formed is homogeneous in structure; it has a very sharp interface with the liquid phase. In the event of an inhomogeneity in the structure of the precipitates formed, density gradients should appear in the volume of the solid phase, and density discontinuities on the observed scanning curves would have a flat appearance. In addition, the distribution of the scattering intensity along a portion of the solid phase also indicates its homogeneity, since there are no significant deviations from the average density on the scanning curves. Thus, when studying the process of homogeneous precipitation of aluminum oxyhydrate, the factors influencing the process (temperature, concentration of reagents, pH of the medium, etc.) are determined, the uniformity of the formed sediment.

Figure 5 Intensity of scattering of laser radiation when scanning along the axis of the capillary.

Formulation of the problem

Consider a substrate system-sol particles formed during precipitation or synthesized earlier. These systems may be of two types. The first type is systems that are characterized by a weak interaction between the substrate and the particle of the sol, and the second is a system with a strong interaction between the substrate and the sol particle. Accordingly, various mechanisms for depositing sol particles on the substrate surface are possible. In the case of the first type of system, the growth of the gel film on the substrate goes along the island mechanism. For a second type of system, a uniform static filling of the surface with sol particles is observed. Let us consider in more detail the island mechanism of sol particles on a substrate.²⁴ Suppose that the islets of the gel grow in the form of a hemisphere, and after the collision, the growth in the contact points ceases. In other accessible directions, the islets continue to grow in the form of spherical segments according to the corresponding law. Certain laws of growth of gel islets are the task of this work. The model is applicable for the case when the colliding islands become fused into a continuous gel film similarly to the solid-phase interaction. Consider the gel film at a certain time t. The Z axis is directed along the normal to the surface of the substrate. We denote by S(Z,t) the specific (per unit area of the substrate) cross-section of the film at height Z. At any time, the function S(Z,t) monotonically decreases in height from the surface of the substrate: S(0,t)=S(t) (the degree of filling the substrate with gel at the time t); S(Z,t)=0 at Z ≥ R_m(t) (the radius of the largest islet). For the current specific volume of the gel film, we have:

$V\left(t\right)=\underset{0}{\overset{\infty }{{\displaystyle \int }}}S\left(Z,t\right)dZ$    (1)

The process of its growth in time determines the rate of increase in the volume of the gel film. When the sol is deposited, a Z-flux of particles of a given intensity J (m^-2s^-1). The particles trapped in the gel film are captured by it, and the substrates found on bare areas migrate along it in accordance with the coefficient of surface diffusion D. If during the lifetime before desorption (t), the particles do not collide with the contour of the gel film, they leave the substrate, moving along it for a distance on the order of the diffusion length. In the film of the gel, only particles from the contiguous strip of food with a width of L_l. Thus, the growth of the gel film is due to the addition of all particles falling from the liquid phase into the zone consisting of the region occupied by the film and the poles of the supply. The effective specific area of the film S_l, with which all particles are absorbed, will be equal to the area of the film, taking into account the increase in the radius of all its islands by an amount L_l, those. The gel formed during precipitation is a porous structure consisting of sol particles that are packed in a specific way. Therefore, the true volume of the gel will differ from the volume of particles trapped by the gel. Thus, knowing the particle size of the sol v, and the porosity of their packing in the gel structure α, we can write the velocity equation, which describes the increase in the volume of the gel film:

$\frac{dv\left(t\right)}{dt}=JvS\left(R\left(t\right)+L_l\right){\left(1-\alpha \right)}^{-1}$    (2)

In real systems, there are practically no mono-fractional composition systems [10], therefore, taking into account that, and the flux of sol particles does not depend on their size. We shall average over the particle size of the sol, taking into account the distribution function of the sol F(r). Equation (2) is transformed to the form:

$\frac{dv\left(t\right)}{dt}=\frac{4\pi }{3}JS\left(R\left(t\right)+L_l\right){\left(1-\alpha \right)}^{-1}\underset{0}{\overset{\infty }{{\displaystyle \int }}}{r}^{3}F\left(r\right)dr$    (3)

In the case of F(r) as a δ-function, equation (3) is transformed to the form (2). Equations (1) and (2) are equations of a self-consistent model that define the growth law R(t). Let us consider specific models of the processes of nucleation and growth of a gel film on the substrate surface.

Creating a processes model of gel-film birth and growth

By analogy with the processes of chemical vapor deposition of metals on the surface of the substrate, two basic models for nucleation of film growth centers are also possible for sol particles.²⁵ The model of continuous nucleation, when growth centers appear at random points of a free surface with intensity J(r) (?^-2?^-1) during the entire process (α-model)²⁶ and the instantaneous nucleation model, when all the centers are present on the substrate from the very beginning of the process and are randomly distributed with a charge N(m) (β-model)²⁷ For the α-model, the film of the gel, given by the formula, increases the probability of not capturing a certain point at a distance Z from the surface of the substrate to the instant of time t:

$p\left(Z,t\right)=\exp \left(-\underset{0}{\overset{t}{{\displaystyle \int }}}M\left(\tau \right)d\tau \right)$    (4)

Here ?(τ) ?The probability of the appearance of an embryo at time τ in a circle of radius  with the center at a given point, which is able to absorb this point at time τ, with the proviso that τ to nucleation in this disk was not. This probability is:

$M\left(t\right)=\pi J\left(t\right)\left(R^2\left(t\right)-Z^2\right)$    (5)

Given that, we have for the α-model:

$S\left(Z,t\right)=1-\exp \left(-\pi \underset{0}{\overset{t}{{\displaystyle \int }}}J\left(t\right)\left(R^2\left(t\right)-Z^2\right)dt\right)$    (6)

For the β-model, p(Z,t) coincides with the probability of absence of condensation centers in the circle ${\left(R^2\left(\tau \right)-Z^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ , and, taking into account their Poisson distribution, we obtain:

$S\left(Z,t\right)=1-\exp \left(-\pi N\left(R^2\left(\tau \right)-Z^2\right)\right)$    (7)

We substitute equation (6) and (7) into formula (1) and obtain for α-model:

$V\left(t\right)=\underset{0}{\overset{\infty }{{\displaystyle \int }}}\left(1-\exp \left(-\pi \underset{0}{\overset{t}{{\displaystyle \int }}}J\left(t\right)\left(R^2\left(t\right)-Z^2\right)dt\right)\right)dZ$    (8)

for the β model:

$V\left(t\right)=\underset{0}{\overset{\infty }{{\displaystyle \int }}}\left(1-\exp \left(-\pi N\left(R^2\left(\tau \right)-Z^2\right)\right)\right)dZ$    (9)

The degree of filling of the substrate at time t for α- and β-models is, respectively:

$S\left(t\right)=1-\exp \left(-\pi \underset{0}{\overset{t}{{\displaystyle \int }}}J\left(t\right)R^2\left(t\right)dt\right)$    (10)

And

$S\left(t\right)=1-\exp \left(-\pi N{R}^2\left(t\right)\right)$    (11)

Taking into account the diffusion length L₁, from equations (10) and (11) we obtain the second self-consistency equation. For the α-model, it takes the form:

$\frac{dV}{dt}=JV\left(1-\exp \left(-\pi \underset{0}{\overset{t}{{\displaystyle \int }}}I\left(t\right){\left(R\left(t\right)+L_l\right)}^{2}dt\right)\right)$    (12)

for the β model:

$\frac{dV}{dt}=JV\left(1-\exp \left(-\pi N{\left(R\left(t\right)+L_l\right)}^2\right)\right)$    (13)

The pairs of equations (8), (12) and (9), (13), respectively, are self-consistency equations that determine the growth law R(t). In the most general form, the growth law R(t) can be obtained from equations (1) and (2). We differentiate the function of the specific volume of the gel film (1) along the radius of the gel islands, and we obtain:

$\frac{dV}{dR}=\underset{0}{\overset{\infty }{{\displaystyle \int }}}\frac{\partial S\left(Z,t\right)}{\partial R}dZ$    (14)

Dividing equation (2) by equation (14), we obtain a differential equation describing the growth law of the islets of the gel:

$\frac{dR}{dt}=\frac{dV}{dt}\cdot \frac{dR}{dV}=\frac{JVS\left(R\left(t\right)+L_l\right)}{{{\displaystyle \int }}_{{}_0}^{{}^{\infty }}\frac{\partial S\left(Z,t\right)}{\partial R}dZ}$    (15)

Integrating equation (15), we obtain the law of growth in the general form:

$\underset{0}{\overset{R}{{\displaystyle \int }}}\frac{{{\displaystyle \int }}_{{}_0}^{{}^{\infty }}\frac{\partial S\left(Z,t\right)}{\partial R}dZ}{S\left(R\left(t\right)+L_l\right)}dR=JVt$    (16)

For specific models of nucleation and growth of a gel film, the growth laws can be obtained from pairs of self-consistency equations (8), (12) and (9), (13), using the transformations described above. In this case, the α-model will be described by the following equation:

$\underset{0}{\overset{R}{{\displaystyle \int }}}\frac{2\pi \left({{\displaystyle \int }}_{{}_0}^{{}^t}IRdt\right)\left({{\displaystyle \int }}_{{}_0}^{{}^{\infty }}\exp \left(-\pi {{\displaystyle \int }}_{{}_0}^{{}^{\infty }}I\left(R^2-Z^2\right)dt\right)dZ\right)}{1-\exp \left(-\pi {{\displaystyle \int }}_{{}_0}^{{}^t}I\left(R+L_l\right)dt\right)}dR=JVt$    (17)

and the β-model will get the following form:

$\underset{0}{\overset{R}{{\displaystyle \int }}}\frac{2\pi RN\left({\displaystyle \underset{0}{\overset{\infty }{\int }}\exp }\left(-\pi N\left(R^2-Z^2\right)\right)dZ\right)}{1-\exp \left(-\pi N\left(R+L_l\right)\right)}dR=JVt$    (18)

The numerical integration of Eq. (17) is complicated because the dependence R (t) of the island radius on time is explicitly indicated on the left-hand side of the equation. Therefore, integrating this equation, it is required to specify a specific form of the functional R (t) and in one way or another to find the constant coefficients of the chosen functional. Equation (18) is simpler and can be easily integrated numerically to obtain a specific type of curves reflecting the law of growth of a thin film on the substrate surface.

Calculation of the parameters of films formed

In addition to the deposition law, the process of precipitating the sol particles and forming the gel film will be described by a variety of morphological and kinetic characteristics such as the condensation coefficient, the degree of surface filling, the average film thickness, the surface roughness, the specific surface area. The condensation coefficient γ(t) determines the fraction of condensed particles from the total number of Jt settled by the time point t:

$\gamma \left(t\right)=t^{-1}\underset{0}{\overset{t}{{\displaystyle \int }}}\left(1-\exp \left(-\pi N{\left(R\left(t\right)+L_l\right)}^2\right)\right)dt$    (19)

The coefficient γ(t) characterizes the thickness of the film and allows to determine the amount of substance that must be introduced into the system in order to obtain a film of a given thickness. The degree of filling of the surface of the substrate is expressed by the formula:

$S\left(t\right)=1-\exp \left(-\pi N{R}^2\left(t\right)\right)$    (20)

The most important characteristic of the gel on the substrate is the average, or mass thickness, i.e. the volume per unit of surface, which is related to the condensation coefficient γ(t) by the relation:

$\overline{h}=\gamma \left(t\right)JVt$    (21)

Or

$\overline{h}=\underset{0}{\overset{\infty }{{\displaystyle \int }}}hf\left(h\right)dh$    (22)

Where: f(h) — function of the density distribution of the gel film thickness.

Surface roughness is an important physical characteristic, since surface irregularities cause an increase in friction effect, adhesion of polymers, etc. A quantitative measure of the roughness can be the magnitude of the rms ratio of the local film thickness from the mean value:

${\sigma }^2=\underset{0}{\overset{\infty }{{\displaystyle \int }}}{\left(h-\overline{h}\right)}^{2}f\left(h\right)dh$    (23)

For a rough surface, the density distribution function of the height of each point of the surface has the form:

$f\left(h\right)=p\left(h,t\right)\delta \left(h\right)+\{\begin{array}{c}\frac{\partial p\left(h,t\right)}{\partial h}, 0\le h\le R\\ 0, R\le h\end{array}$    (24)

Where:  – free surface fraction; – Dirac δ-function.

Taking into account (7) and (24) from (23), we obtain:

${\sigma }^2\left(t\right)=\pi N{R}^2\left(t\right)-\gamma \left(t\right)JVt-S\left(t\right)$    (25)

Due to the roughness of the surface, the effect of increasing the specific surface area S_sp of the entire sample is produced. It is easy to see that the specific surface coincides with the area of the free surface and the specific surface of the deposition front:

$S_{уд}=p\left(t\right)+\frac{dV\left(t\right)}{dR}=1-S\left(t\right)+\frac{d}{dR}\underset{0}{\overset{\infty }{{\displaystyle \int }}}hf\left(h\right)dh$    (26)

Hence, in view of (24) we obtain:

$S_{уд}=1-S\left(t\right)+2\pi NR\left(t\right)\left(R\left(t\right)-\overline{h}\right)$    (27)

An important point is that the values of the thickness of the gel film, the roughness and the surface area are universal functions of the degree of filling of the surface and do not depend on the specific model of the process mechanism.

The use of homogeneously precipitated aluminum hydroxide as a binder

The method of homogeneous deposition of the binder is based on the gradual release of the precipitant when a substance is decomposed directly in the volume of the solution containing the precipitated reagent. As an example, the results of experiments on obtaining a lightweight heat-shielding material. In this case, the method of precipitation of aluminum hydroxide is realized in the interaction of aluminum chloride with ammonia evolved in a homogeneous medium during decomposition of urea. Since urea does not hydrolyze at room temperature, in the absence of heating, the hydroxide does not precipitate, and the medium remains homogeneous. When heated to a temperature above 70?, hydrolysis of urea occurs. Because of this process, in the reaction medium formed substances such as N?₃, ??₂, ??^— , It becomes possible to form a precipitate of hydrated alumina. Because the release of NH₃, ??^— occurs uniformly throughout the entire volume of the solution and its speed is easily regulated, it is possible to avoid local super saturations and, consequently, the heterogeneity of precipitation. This technique allows achieving a uniform composition and structure of the sediment. The preparation of a precipitate in a homogeneous medium leads to the formation, at the first stage of the process, of the smallest centers of aluminum hydroxide, which subsequently grow in time. If there are nucleation centers in the system, the growth of particles occurs primarily at these centers. The fibers of the mullite-silica composition present in the system in the production of lightweight materials are, therefore, centers of nucleation. The process of precipitation of aluminum hydroxide particles proceeds primarily on them, covering them with a thin film. The resulting film acts as a gluing agent, which, upon subsequent drying, undergoes a gel-xerogel transformation and becomes a solid that binds the fibers into a single monolith. The resulting materials have a developed specific surface area and porosity. Studies of the materials obtained earlier showed a significant dependence of their properties on the density. The dependence of the tensile strength at 10% compression on the density is shown in Figure 6. It can be seen from Fig. 6 that this dependence is of a complex nature, although it clearly shows the main tendency of the growth of strength characteristics with increasing sample density. Since the density of the material is primarily determined by the amount of the precipitated binder, it can be assumed that at densities of less than 0.17 g/cm³, the presence of a small amount of binder does not allow for sufficient strength and sufficient amount to bond all the filler fibers in the structure of the resulting material. At the same time, a very light but low-strength material is formed. In the case of a large binder content, strength increases, and its growth becomes sufficiently monotonic, although it remains at a very low level. One of the reasons for the formation of a weak contact between the fibers can be explained by the presence in the system of ammonium chloride formed as a result of the reaction:

Ammonium chloride during drying is released in the form of fine particles, which destroy the structures of the formed gels, drastically reducing their strength characteristics. Thus, the method of homogeneous precipitation of the binder on the surface of the fibers does not allow obtaining sufficiently strong materials; however, these materials have an increased thermal stability.

Figure 6 Dependence of the compressive strength on the density of materials with a binder based on aluminum hydroxide obtained by homogeneous precipitation.

In this work, studies have been conducted homogeneous precipitation process hydrated alumina. The variants of this process are considered. As the most technological embodiment of this process, precipitation of hydrated alumina from its salts using auxiliary substances. As such, auxiliary substances used urea. The hydrolysis of urea proceeds slowly even with heating, which allows the homogeneous precipitation of hydrated alumina under the most mild conditions. It is shown that the process of hydrolytic precipitation in the aluminum salt- urea system proceeds according to the dissociative mechanism S_N1. The S_N1 mechanism is characterized by a two-step mechanism, in which the first step is slow monomolecular hydrolytic dissociation, followed by a rapid coordination reaction with the second reagent. To determine the nature of the interaction of the aluminum salt with alkaline agents, experiments were conducted on potentiometric titration of the aluminum salt with solutions of ammonia and sodium hydroxide in the presence of various amounts of ammonium chloride and urea. When titrating with sodium hydroxide solution, the process proceeds to the formation of sodium aluminate, titration with a solution of ammonia produces a precipitate of hydrated alumina. Addition of ammonium salts shifts the equilibrium of the hydrolysis reaction towards the formation of aluminum hydroxide. The presence of urea virtually does not affect the course of the deposition process. To determine the uniformity of the formed sediment, the laser radiation scattering method. For these purposes, a special installation was created, which makes it possible to scan a capillary with the resulting solution by means of a focused laser beam. The homogeneity of the formed precipitate of hydrated aluminum oxide was found. For the practical implementation of the homogeneous deposition method, studies were carried out on the use of homogeneously precipitated aluminum hydroxide as a binder in lightweight fibrous refractory materials. In the proposed embodiment of the process for obtaining the material, the precipitation of the aluminum hydroxide particles proceeds primarily on the filler fibers, covering them with a thin film. The resulting film acts as a gluing agent. After drying and calcination, the precipitated gel, in the form of a thin film, becomes a solid that binds the fibers into a single monolith. The resulting materials have a developed specific surface area and porosity. Based on an analysis of the regularities of deposition of solid colloidal particles on the surface of substrates, two possible models of the process. This α-model, which is a process of continuous nucleation of interaction centers, when the growth centers appear at random points of the free surface with a fixed intensity throughout the process and the β-model, which is the instantaneous nucleation of these centers, when all the centers are present on the substrate from the very beginning of the process and distributed chaotically over the surface of the substrate. Based on the proposed models, the average values of the values of the thickness of the gel film, its roughness and the specific surface area are calculated. It was found that these parameters for the products obtained are universal functions of the degree of filling of the surface and do not depend on the specific model of the mechanism of the process.

The use of this model allows us to conduct a predictable synthesis of active sorbents to purify contaminated effluents and to recover valuable components, carrier for catalysts in the petrochemical industry, with a developed and easily accessible external surface on strong substrates, and to obtain heat-resistant composite materials.

None.

The author declares that there are no conflicts of interest.

1. Kudryavtsev P. Heat‒resistant inorganic binders. Journal Scientific Israel‒Technological Advantages. 2017;19(2):32‒37.
2. Kudryavtsev P, Figovsky O. Nanomaterials based on soluble silicates. LAP Lambert Academic Publishing. 2014;241.
3. Kudryavtsev P, Kudryavtsev N. Nanocomposite materials based on soluble aluminum compounds. Journal Scientific Israel‒Technological Advantages. 2017;19(3):40‒76.
4. Kudryavtsev PG, Kudryavtsev NP, Figovsky OL. The soluble aluminum compounds and nanocomposite materials based on them. Part I. Nanotehnologii v stroitel’stve=Nanotechnologies in Construction. 2018;10(1):37–62.
5. Kudryavtsev PG, Kudryavtsev NP, Figovsky OL. The soluble aluminum compounds and nanocomposite materials based on them. Part II. Nanotehnologii v stroitel’stve=Nanotechnologies in Construction. 2018;10(2):63–85.
6. Dzisko VA. Basics of methods for the preparation of catalysts. Novosibirsk Science. 1983.
7. Betenekov ND, Vasilevsky VA, Nedobukh TA, et al. Radiochemical study of thin films. II Sorption of uranium by thin‒layered titanium hydroxide under static conditions. Radiochemistry. 1984;4:432‒439.
8. Betenkov ND, Egorov Yu V. Thin‒layer inorganic sorbents in radiochemical analysis. Journal of Analytical Chemistry. 1997;11:1120‒1132.
9. Ketov AA, Fazleev MP, Ismagilov ZR, et al. Method for the preparation of oxide catalysts. Patent of the USSR no 1615945 under the application no 4644450/04.
10. Kudryavtsev PG, Ketov AA, Fazleev MP, et al. Application of oxide films on the ceramic substrate using sol‒gel method. Physico‒chemical basis for processing of poor natural raw materials and industrial waste in the production of heat‒resistant materials. Abstracts book of the All‒Union Conf. 1989;1.
11. Kudryavtsev PG, Kropacheva MV. Homogeneous precipitation of aluminum oxyhydrate. Collection of articles: Prospects for the development of natural sciences in higher education, Perm. 2001;75‒80.
12. Kudryavtsev PG, Volkhin VV. Sol‒gel processes and some of its technological applications. Abstracts book of seminar reports: Sol‒gel processes of inorganic materials production, Perm. 1991;3‒5.
13. Kudryavtsev PG, Kropacheva MV, Kavalerova OB, et al. The use of sol‒gel processes for the production of ultra‒lightweight composite materials. Collection of articles: Composite materials based on dispersed systems, Perm. 1991;19‒23.
14. Kudryavtsev PG. Methods for producing oxide lightweight refractory materials. Collection of articles: Composite materials based on disperse systems, Ekaterinburg: UrB RAS. 1994;4‒21.
15. Kudryavtsev P. Heat‒resistant inorganic binders. Journal Scientific Israel‒Technological Advantages. 2017;19(2):32‒37.
16. Kudryavtsev P. Colloidal Solutions in the Preparation of Inorganic Composites and Ceramics. Journal “Scientific Israel‒ Technological Advantages". 2018;20(3):59‒70.
17. Kudryavtsev P. Methods of synthesis, properties and applications of silica‒sols for obtaining composite materials. Part I. Electronic scientific journal Engineering Bulletin of the Don. 2018;3:1‒34.
18. Kudryavtsev P. Methods of synthesis, properties and applications of silica‒sols for obtaining composite materials. Part II. Electronic scientific journal Engineering Bulletin of the Don. 2018;3:1‒22.
19. Wasserman IA. Chemical precipitation from solutions. L Chemistry. 1980.
20. Tikhonov VN. Analytical chemistry of aluminum. M Science. 1971. C. 58.
21. Kudryavtsev PG, Klyachkin Yu S. Modification of the surface of materials due to the deposition of sol particles, Abstracts of Republican scientific and technical conference "Surface formation and interfacial interactions in composites". Izhevsk. 1987;11‒13.
22. Kudryavtsev PG, Klyachkin Yu S. Mathematical modeling of the processes of surface modification of materials due to deposition of colloidal particles, Abstracts of regional scientific and technical conference. "Mathematical modeling in the processes of production and processing of polymeric materials." Perm. 1908;17‒18.
23. Kropacheva MV. Study of the processes of homogeneous precipitation of aluminum oxyhydrate. In: Composite materials based on disperse systems, Ekaterinburg. 1994;41‒46.
24. Kudryavtsev PG. Modeling of the growth processes of particles of metal oxide sols. Collection of articles: Physicochemical Properties of Composites and Organic Reagents with Active Functional Groups. Sverdlovsk. 1991;83‒86.
25. Trofimov VI, Osadchenko VA. Self‒consistent model of the kinetics of the volume growth of a thin plate. Surface. Physics, Chemistry, Mechanics. 1986;1:28‒38.
26. Belenky DZ. Geometric‒probabilistic models of crystallization, phenomenological approach. Moscow, Science. 1980;88.
27. Geguzin A Ya. Physics of sintering. Moscow: Science. 1984;312.