This paper presents the prediction of the phase behavior of methylamine/water refrigerant mixture. To do so, two equations of state were investigated: PC-SAFT and GEOS. The adjustable specific parameters of pure fluids are determined by regression of vapor pressure and saturated liquid and vapor density data. The calculations show that the GEOS model predicts more accurately the thermodynamic properties of pure fluids, in particular in the vicinity of the critical point. For binary mixtures, the cross-interaction parameters are obtained by regression of the vapor-liquid equilibrium data available in the literature. The comparison between predicted and experimental data reveals that both investigated EOS have comparable performance with slight superiority to GEOS when approaching the critical temperature of methylamine. Finally, since the GEOS model is more mathematically tractable and more accurate when applied to pure fluids, it is adopted for the correlation and prediction of the thermodynamic properties of the methylamine/water system.

Keywords: methylamine, water, thermodynamic, properties, equations, PC SAFT, GEOS

Absorption refrigeration machines represent a promising solution in order to circumvent the increase in electric power consumption due to air-conditioning and refrigeration particularly in the summer period. This technique for the production of cold exhibits some interesting advantages. By using heat as driving energy, such that released by the combustion of natural gas or LPG, it is possible to by-pass the usage of electric power. Moreover, this method allows the valorization of the thermal emissions of intermediate temperatures. The electric power needed is marginal (i.e., essentially for circulation pumps and control systems). However, the absorption cycles are much more complex in comparison to the vapor compression machines. On the energy performance level, the single-effect absorption refrigeration chillers present a COP (between 0.5 and 0.7) lower than its counterpart obtained with the vapor compression systems, even when brought back to the primary energy. Hence, the absorption technique for production of cold is not energy efficient. However, this concern becomes secondary if the supplied driving heat is inexpensive (e.g., heat from thermal discharges or from thermal solar energy plants). Under these circumstances, the absorption refrigeration may well constitute a viable alternative to the vapor compression systems. During last decades, many studies in this field have focused on the standard systems water-ammonia and water-LiB_r solutions and theoretical and experimental investigations of other alternative working fluids. This quest was aimed at the development of techniques, which improve absorption systems performance and make them economically competitive when compared to the conventional compression vapor systems.^1–21 The absorption heat transformers are also investigated with interest for waste-heat reutilization within industrial processes, due to their favorable economics and mild environmental effects.^22–28

The thermal performance of an absorption refrigeration system is greatly dependent on the physical and chemical properties of the working fluids used.^29–31 Up to now, only two refrigerant mixtures, NH₃-H₂O and LiBr- H₂O, are widely employed in commercialized absorption chillers. However, these working fluids present some limitations. Firstly, the LiBr- H₂O system works at high vacuum levels, which are difficult to maintain. Secondly, this mixture cannot be used for air-cooled units under high ambient air temperatures due to salt crystallization.^32–34 Further, with water as refrigerant temperatures lower than 0^°C are not possible. On the other hand, the NH₃-H₂O mixture is such that the boiling temperature difference between the absorbent (water) and refrigerant (ammonia) of is not sufficiently large, which makes necessary a rectification step at the exhaust of the boiler to ensure the required purity of the desorbed ammonia. In addition, the driving heat has to be supplied to the generator at a high temperature of about 180°C. In order to circumvent the limitations of the NH₃-H₂O system, a large number of studies has focused on the search for alternative and more appropriate fluid mixtures.^35–37 The looked-for working fluid system should exhibit the desired properties in particular keep the condenser pressure at the lowest possible level above one bar, allowing low generator temperatures, and hence making the use of low-grade thermal sources as driving heat. A potential candidate is water/methylamine system with methylamine replacing ammonia as refrigerant. It has been found that the thermodynamic properties of the methylamine–H₂O mixture are interesting for application in absorption refrigeration.^38–40 Vapor pressures and driving temperatures data indicate that thermal energy sources at low temperatures may be used (e.g., solar, geothermal and waste heat of industrial and commercial processes). However, methylamine is a refrigerant that has been poorly investigated in the literature. Indeed, property data for the pure fluid and its solutions with several solvents are scarcely reported in the literature. Some thermodynamic properties of methylamine–H₂O mixtures are found in references,^41–51 occasionally expressed in empirical expressions for each property. Even, if such relations reproduce fairly the experimental data,⁴⁰ the thermodynamic consistency of the calculated properties from different relations is not ensured.

Coherent prediction of thermodynamic properties of refrigerant mixtures is of primordial importance for the reliable design of absorption refrigeration machines. The objective of present study is to develop, basing on the scarce published data for methylamine/water system, a reliable thermodynamic model for predicting and calculating phase equilibria and for the design and dimensioning of absorption refrigerating machines relevant properties of the mixture. The proposed models should possess a sufficient accuracy over a wide range of conditions and involve a minimum number of adjustable and easily accessible parameters. The equations of state (EOS) represent the best choice for this purpose; in fact, all the thermodynamic properties can be consistently derived from an EOS when it expresses a thermodynamic potential. In the following, two EOS models will be investigated and compared: PC-SAFT and GEOS. The PC-SAFT (Perturbed Chain Statistical Associating Fluid Theory) equation of state is based on a theoretical approach. Applying the Barker-Henderson perturbation theory to a reference hard-chain fluid, a valuable variant of the original SAFT model^52–53 is obtained and applied to correlate asymmetric, highly non-ideal, and associating fluids.^54–62 The general cubic equation of state GEOS considered in the present paper is a semi-empirical approach.^63–67 GEOS is a four-coefficient cubic EOS that permits the critical compressibility factor adjustment, ZC, instead of the prediction of a universal value. Hence, the saturation property predictions for polar compounds and their mixtures are improved due to this added flexibility. The predictions of thermodynamics properties by both investigated models will be confronted to their corresponding experimental data. This will shed light to which EOS is more appropriate and accurate in the correlation and prediction of the thermodynamic properties of the methylamine/water mixture in wide ranges of temperature and pressures comprising the typical operating domain of absorption refrigeration cycles.

PC-SAFT equation of state

In the Perturbed Chain SAFT (PC–SAFT) equation of state, the fluid molecules are considered a shard chains of spherical segments with interaction potential divided into

1. a repulsive part
2. an attractive part

The repulsive contribution is modeled with a hard chain reference fluid in which no attractions are present. The contributions describing the hard chain term and the association interaction are expressed identically to those embedded in the original SAFT EOS. Whereas, a perturbation-theory of second order is applied to the hard–chains instead of hard-spheres to modify the dispersion-term. This allows us to account for the effect of the non-spherical shape of the molecules on the number of intermolecular interactions. Thus, the dispersion term is a function of segment number m. Accordingly the molar reduced Helmholtz free energy is expressed as the sum of a reduced ideal gas contribution $a^O$ and a reduced residual contribution ($a^r$ ). The latter is composed of three terms: $a^{hc}$ , $a^{disp}$ and $a^{assoc}$ corresponding to hard-chain, dispersion and association interactions, respectively:^54–58

$a=\frac{A}{RT}=a^{\text{ο}}+a^r=a^{\text{ο}}+a^{hc}+a^{disp}+a^{assoc}$ (1)

In the PC–SAFT EOS, each non-associating compound in the mixture is characterized by three pure–component parameters (the segment number m_i, the segment diameter σ_i, and the dispersion energy parameter ${\epsilon }_i/k$ .The average segment number of a mixture, $\overline{m}$ is estimated from the segment numbers of its components, m_i, as follows:

$\overline{m}={\displaystyle \sum }_i{x}_i{m}_{{}_i}$ (2)

The segment diameter,σ_ij , and dispersive energy, ${\epsilon }_{ij}/k$ for a pair of unlike segments are obtained by the conventional Berthelot–Lorentz combining rules:

${\sigma }_{ij}=\frac{1}{2}\left({\sigma }_i+{\sigma }_j\right)$ (3)

$\frac{{\epsilon }_{ij}}{k}=\left(1-k_{ij}\right)\sqrt{\frac{{\epsilon }_i}{k}\frac{{\epsilon }_j}{k}}$ (4)

where K_ij is an adjustable binary parameter introduced to correct cross–dispersive interactions.

To give more flexibility to this model in predicting methylamine/water system properties, Reid-Panagiotopoulos mixing rule depending on composition is applied and Equation (4) is replaced by:^59–61

$\frac{{\epsilon }_{ij}}{k}=\left[1-k_{ij}+\left(k_{ij}-k_{ji}\right)x_i\right]\sqrt{\frac{{\epsilon }_i}{k}\frac{{\epsilon }_j}{k}}$ (5)

$\frac{{\epsilon }_{ij}}{k}=\left[1-k_{ij}+\left(k_{ij}-k_{ji}\right)x_i\right]\sqrt{\frac{{\epsilon }_i}{k}\frac{{\epsilon }_j}{k}}$ (6)

Where $k_{ji}$ and $k_{ji}$ are two adjustable empirical binary cross-interaction parameters.

Association contribution

Basing on Wertheim’s first–order perturbation theory, Chapman et al.^52,53 proposed an association model to represent the interactions due to the short–range association (hydrogen bonding) $a^{assoc}$ . This model is retained in this paper. Basing on this theory, a molecule is supposed to have one or more association sites that can form hydrogen bonds. Two additional pure-component parameters, the association energy, ${\epsilon }^{A_i{B}_i}/k$ and the effective association volume, $K^{(A_i{B}_i)}$ are used to characterize the associating interactions between unlike association sites A_i and B_i. Hence, a self-associating substance is modeled with five pure–component parameters. The association-site number on a molecule and the potential site–site interactions have a powerful influence on the fluid structure, and consequently on the phase equilibria. Thus, a careful chose should be considered. The reduced association Helmholtz free energy of a mixture can be written as a mole fraction weighted linear combination of the free energies of the pure components:^59–62

$a^{assoc}={\displaystyle \sum }_i{x}_i\left[{\displaystyle \sum }_{A_i}\left(\ln X^{A_i}-\frac{X^{A_i}}{2}\right)+\frac{M_i}{2}\right]$ (7)

where X^Ai is the mole fraction of molecules i that are not bonded at site A. The monomer fractions X^Ai of the components of the mixture are calculated by resolving of the non–linear system of equations:

$X^{A_i}={\left(1+N_{Av}\rho {\displaystyle \sum }_j{x}_j{\displaystyle \sum }_{B_j}{X}^{B_j}{\Delta }^{A_i{B}_j}\right)}^{{}^{-1}}$ (8)

The summation ∑_Bjcovers all sites on molecule j and ∑_j all components of the system. ${\Delta }^{A_i{B}_j}$ represents the association bond strength between sites A and B on molecules i and j, respectively. ${\Delta }^{A_i{B}_j}$ is expressed as a function of the association volume, ${\kappa }^{A_i{B}_j}$ the association energy, $\frac{{\epsilon }^{A_i{B}_j}}{kT}$ and the radial distribution function,$g_{ij}^{hs}(d_{ju})$ , as follows:

${\Delta }^{A_i{B}_j}={\sigma }_{ij}^3{\kappa }^{A_i{B}_j}{g}_{ij}^{hs}\left[\text{exp}\left(\frac{{\epsilon }^{A_i{B}_j}}{kT}\right)-1\right]$ (9)

The cross–association interaction coefficients between two different associating components can be expressed with pure–component parameters using the following simple combining-rules:

$\frac{{\epsilon }^{A_i{B}_j}}{k_b}=\sqrt{\frac{{\epsilon }^{A_i{B}_i}}{k}\frac{{\epsilon }^{A_j{B}_j}}{k}}$ (10)

${\kappa }^{A_i{B}_j}=\sqrt{{\kappa }^{A_i{B}_i}{\kappa }^{A_j{B}_j}}$ (11)

Resolution of the association term

The calculation of self-associating compounds properties requires the $a^{assoc}$ term and its derivatives with respect to molar density, temperature and molar fractions. Prior to the determination of $a^{assoc}$ for a pure component, the definition and specification of all non–zero site–site interactions must be given. Solely not vanishing values of ${\Delta }^{AB}$ are used to calculate the monomer fractions,$X^A$ In general, equations (6) are not $X^A{}^{-}$ -explicit. In order to simplify their resolution, some approximations, aimed to reduce the number of adjustable parameters, are considered:^52–53

The association strength $\Delta$ is set equal to zero for like atom interactions (e.g., oxygen-oxygen, hydrogen-hydrogen), and symmetrical for unlike atom interactions.

For a specific fluid, the monomer fractions $X^A$ are equal $(X^A=X^B=\mathrm{....}=X)$ .

The monomer fraction X for a pure compound exhibiting two associating sites becomes:

$X=\left(-1+\sqrt{1+4N_{Av}\rho \text{Δ}}\right)/\left(2N_{Av}\rho \text{Δ}\right)$ (12)

In the case of four associating sites it writes:

$X=\left(-1+\sqrt{1+8N_{Av}\rho \text{Δ}}\right)/\left(4N_{Av}\rho \text{Δ}\right)$ (13)

For mixtures composed of self and cross-associating components, the monomer fractions X_i for all associating compounds can be simultaneously evaluated iteratively from the system of equations (6) and considering the above given assumptions.^{59, 61, 62}

For the binary methylamine/water mixture investigated in this paper, X₁ and X₂are evaluated by solving the equation system:^61,62

$x_1{N}_{Av}\rho {\text{Δ}}_{11}{X}_1^2+\left(1+2 x_2{N}_{Av}\rho {\text{Δ}}_{12}{\text{ X}}_2\right)X_1-1=0$ (14)

$2 x_2{N}_{Av}\rho {\text{Δ}}_{22}{X}_2^2+\left(1+x_1{N}_{Av}\rho {\text{Δ}}_{12}{\text{ X}}_1\right)X_2-1=0$ (15)

Methylamine (component 1) is modeled with a 2B-association-scheme and water (component 2) is represented with a 4C-association-scheme. Once the fractions $X_i$ determined, their derivatives with respect to their different variables (temperature, molar density and molar compositions x_i) are evaluated as well as the contribution of the association interactions. The thermodynamic properties of a system can be derived from the reduced Helmholtz free energy with the flowing relations:⁵⁹

$P=RT\rho \left[1+\rho {\left(\frac{\partial a^r}{\partial \rho }\right)}_{T,x_i}\right]$ (16)

$\text{ln}{\phi }_k=a^r+{\left(\frac{\partial a^r}{\partial x_k}\right)}_{T,\rho ,x_{i\ne k}}-{\displaystyle \sum }_{j=1}^c{x}_j{\left(\frac{\partial a^r}{\partial x_j}\right)}_{T,\rho ,x_{i\ne j}}+\left(Z-1\right)-\text{ln}Z$ (17)

$\frac{h\left(T,P,x_i\right)}{RT}=\frac{h^{\text{ο}}\left(T,x_i\right)}{RT}-T{\left(\frac{\partial a^r}{\partial T}\right)}_{\rho ,x_i}+\left(Z-1\right)$ (18)

$\frac{s\left(T,P,x_i\right)}{R}=\frac{s^{\text{ο}}\left(T,P,x_i\right)}{R}-a^r-T{\left(\frac{\partial a^r}{\partial T}\right)}_{\rho ,x_i}+\text{ln}Z$ (19)

GEOS cubic equation of state

The used GEOS is a general four-parameter cubic equation of state:^63–67

$P=\frac{RT}{\overline{V}-b}-\frac{a}{{\left(\overline{V}-d\right)}^2+c}=\frac{RT\rho }{1-b\rho }-\frac{a{\rho }^2}{{\left(1-d\rho \right)}^2+c{\rho }^2}$ (20)

For a pure fluid, the four coefficients a, b, c and d are expressed as follows:

$a={\text{Ω}}_a\frac{R^2{T}_C^2}{P_C}{\left(\alpha \left(T_r\right)\right)}^2 ; b={\text{Ω}}_b\frac{R{T}_C}{P_C}$ (21)

$c={\text{Ω}}_c\frac{R^2{T}_C^2}{P_C^2} ; d={\text{Ω}}_d\frac{R{T}_C}{P_C}$ (22)

Let $Tr$ ,$Pr$ and $\rho r$ represent the reduced variables, and ξ_c is the calculated value of the critical compressibility factor, respectively. At the critical point we have:

$P_r=1 ; {\left(\frac{\partial P_r}{\partial {\rho }_r}\right)}_{T_r}=0$ (23)

${\left(\frac{{\partial }^2{P}_r}{\partial {\rho }_r^2}\right)}_{T_r}=0 ; {\alpha }_c={\left(\frac{\partial P_r}{\partial T_r}\right)}_{{\rho }_r}$ (24)

α_c is the Riedel’s criterion.

At the critical point,$Tr=1$ and $Pr=1$ he expressions for the constants Ω_a,Ω_b,Ω_c;and Ω_dare then:

${\text{Ω}}_a={\left(1-B\right)}^3 ; {\text{Ω}}_b={\xi }_c-B$ (25)

${\text{Ω}}_c={\left(1-B\right)}^2\left(B-0.25\right);{\text{ Ω}}_d={\xi }_c-\frac{1-B}{2}$ (26)

$B=\frac{1+{\gamma }_1}{{\alpha }_c+{\gamma }_1}$ (27)

For the attractive term, the temperature-dependent alpha function is defined as:

$\alpha \left(T_r\right)=1+{\gamma }_{1}y+{\gamma }_2{y}^2+ {\gamma }_3{y}^3 , \text{for }{T}_r\le 1$ (28)

$\alpha \left(T_r\right)=1+{\gamma }_{1}y , \text{for }{T}_r>1$ (29)

$y=1-\sqrt{T_r}$ (30)

where γ₁, γ₂ and γ₃ are component-specific adjustable parameters. The experimental values of the critical constants and the accentric factor are used in order to deduce the Riedel factor α_c from the relation:

${\alpha }_c=5.808+4.98 \omega$ (31)

Thus, in this model, a pure fluid is characterized by 4 adjustable parameters: γ₁, γ₂, γ₃ and ξ_c.

The mixing rules for mixtures are:

$a={\displaystyle \sum }_i{\displaystyle \sum }_j{x}_i{x}_j{a}_{ij}$ (32)

$a_{ij}=\left[1-k_{ij}+\left(k_{ij}-k_{ji}\right)x_i\right]\sqrt{a_i{a}_j} , k_{ii}=k_{jj}=0$ (33)

$b={\displaystyle \sum }_i{\displaystyle \sum }_j\left(1-{\lambda }_{ij}\right)x_i{x}_j\left(\frac{b_i+b_j}{2}\right) , {\lambda }_{ij}={\lambda }_{ji}$ (34)

$c=\pm {\displaystyle \sum }_i{\displaystyle \sum }_j\left(1-{\upsilon }_{ij}\right)x_{{}_i}{x}_j\sqrt{c_i{c}_j} , {\upsilon }_{ij}={\upsilon }_{ji}$ (35)

$d={\displaystyle \sum }_i{x}_i{d}_i$ (36)

In equation (35), we use the sign “+” for c_i when c_j> 0, and the sign “‒” for c_i when c_j< 0. Negative values are more common for pure compounds. Then, four adjustable binary cross-interaction parameters are introduced for a binary system: $k_{ij}$ ,$k_{ji}$ , ${\lambda }_{ij}$ and$v_{ij}$

The fugacity coefficient of component j is deduced from a cubic equation of state using the following relation:

$\text{ln}{\phi }_j=-\frac{1}{RT}\underset{\infty }{\overset{\overline{v}}{{\displaystyle \int }}}\left[{\left(\frac{\partial P}{\partial n_j}\right)}_{T,V,n_{i\ne j}}-\frac{RT}{\overline{V}}\right]d\overline{V}-\text{ln}Z$ (37)

The reduced molar enthalpy and entropy write as follows:

$\frac{H\left(T,P,x_i\right)}{RT}=\frac{H^{\text{ο}}\left(T,x_i\right)}{RT}+\frac{1}{RT}\underset{\infty }{\overset{v}{{\displaystyle \int }}}\left[T{\left(\frac{\partial P}{\partial T}\right)}_{V,n_i}-P\right]d\overline{V}+Z-1$ (38)

$\frac{S\left(T,P,x_i\right)}{R}=\frac{S^{\text{ο}}\left(T,P,x_i\right)}{R}+\frac{1}{R}\underset{\infty }{\overset{\overline{v}}{{\displaystyle \int }}}\left[{\left(\frac{\partial P}{\partial T}\right)}_{V,n_i}-\frac{R}{\overline{V}}\right]d\overline{V}+\text{ln}Z$ (39)

Detailed expressions of these thermodynamic properties are given in appendix B.

Ideal-gas properties

The properties of the reference perfect gas mixture of methylamine/water are modeled with the reduced Helmholtz free-energy of a mixture of ideal gases (a^οin Eq. (1)) which is derived from those of the pure ideal-gas of methylamine and water,$a_{01}^{\text{ο}}$ and $a_{02}^{\text{ο}}$ , respectively. They are combined at constant temperature T and constant pressure P according to:

$a^{\text{ο}}\left(T,{\rho }^{\text{ο}},x\right)=x{a}_{01}^o\left(T,{\rho }^{\text{ο}}\right)+\left(1-x\right) a_{02}^o\left(T,{\rho }^{\text{ο}}\right)+x\text{ln}x+\left(1-x\right)\text{ ln}x$ (40)

The term $x\text{ln}x+\left(1-x\right)\text{ ln}x$ results from the mixing entropy of the mixture of ideal gases. The ideal-gas molar density is For a pure ideal-gas, the molar free energy writes:

$A^{\text{ο}}\left(T,{\rho }^{\text{ο}}\right)=U_0^{\text{ο}}-T{S}_0^{\text{ο}}+\underset{T_0}{\overset{T}{{\displaystyle \int }}}{C}_V^{\text{ο}}\left(T\right)dT-T\underset{T_0}{\overset{T}{{\displaystyle \int }}}\frac{C_V^{\text{ο}}\left(T\right)}{T}dT+RT\text{ln}\left(\frac{{\rho }^{\text{ο}}}{{\rho }_0}\right)$ (41)

The molar isochoric heat capacity $C_V^{\text{ο}}$ of a pure ideal gas is expressed as polynomial temperature-dependent function according to:

$C_V^o\left(T\right)={\theta }_0+{\theta }_{1}T+{\theta }_2{T}^2+{\theta }_3{T}^3$ (42)

In this work, the arbitrary reference state of the pure fluid is chosen to be the perfect-gas state at reference temperature $T_0$ and pressure $P_0$ , and consequently the reference molar density is ${\rho }_0^{\text{ο}}=P_0/(R{T}_0)$ . The arbitrary values of the reference molar internal energy $U_0^{\text{ο}}$ and molar entropy $S_0^{\text{ο}}$ of pure fluid are chosen in order to set $H_L=0$ and $S_L=0$ for saturated liquid at the triple-point state of the pure compounds (i.e., 179.70 K for methylamine and 273.16 K for water). The perfect-gas coefficients of the Helmholtz free energy are summarized in Table 1 for both pure methylamine and water. The detailed expressions of $A^{\text{ο}}$ , $H^{\text{ο}}$ and $S^{\text{ο}}$ of a binary mixture are given in the appendix A.

Estimation of pure-component parameters

Adjustable pure-component parameters in the investigated equations of state are evaluated by simultaneously fitting data of vapor pressure, liquid and vapor density at saturation. For this purpose, the following objective function is minimized: $S_1={\displaystyle \sum }_{j=1}^N\left[{\left(\frac{P_j^{exp}-P_j^{cal}}{P_j^{exp}}\right)}^2+{\left(\frac{{\rho }_{L,j}^{exp}-{\rho }_{L,j}^{cal}}{{\rho }_{L,j}^{exp}}\right)}^2+{\left(\frac{{\rho }_{V,j}^{exp}-{\rho }_{V,j}^{cal}}{{\rho }_{V,j}^{exp}}\right)}^2\right]$ (43)

where N represents the number of used experimental data. Vapor-liquid equilibrium data for water are retrieved from,⁷⁰ and for mono-methylamine from^41,71-73 A Fortran program based on the generalized least squares subroutine ODRPACK⁶⁸ and the non-linear equations solver CONLES⁶⁹ is developed for the numerical regression of the literature data. The vapor-liquid phase behavior of a pure fluid are calculated, at a fixed temperature value T, by solving a system of two non-linear equations: chemical potential and pressure equalities. This calculation yields the values of the saturated liquid and vapor molar densities ${\rho }_L^{cal}$ and ${\rho }_v^{cal}$ .

Table 2 & Table 3 summarize the pure-component parameters along with the absolute average deviations AADs for (1) vapor pressure (ΔP), (2) saturated liquid density (Δρ_L) and (3) saturated vapor density (Δρ_V) data, respectively, for PC-SAFT and GEOS models. As can be noted, the GEOS is more accurate than PC-SAFT model in the correlation of the saturation pressures and the liquid and vapor densities of water. For methylamine, the two investigated models have comparable performances in terms of vapor pressure predictions. However, the PC-SAFT model correlates more precisely the methylamine saturated liquid densities than the GEOS equation of state. Figure 1 illustrates the pressure-density diagram for the saturated phase equilibria for H₂O. It is clear that the GEOS cubic EOS is more accurate than the PC-SAFT equation in the correlation of the saturated liquid and vapor phases; especially in the vicinity of the critical state. The enthalpy of vaporization of water is represented in Figure 2 from triple point to critical point. A comparison of the literature data to the theoretical curves shows that the GEOS model is in excellent concordance with data, particularly for high temperatures and pressures. The PC-SAFT model over-estimates the critical point and consequently fails to correlate the properties of pure fluids in the vicinity of the critical region.

Figure 1 Pressure-density diagram of water at saturated liquid and vapor phases.

Figure 2 Molar enthalpy of vaporization of water from triple to critical points.

Vapor-liquid phase behavior of methylamine/water mixture

A bank of N = 183 bibliographical experimental vapor-liquid phase equilibria data for the methylamine/water (Temperature range: 251−423 K and pressure range: 0.009−28.72 bar) has been constituted and exploited to deduce the binary cross-interaction parameters in the PC-SAFT and GEOS equations of state. The same FORTRAN program is used for the calculation of the two-phase vapor-liquid equilibria and the regression of the adjustable binary cross-interaction parameters. For a binary mixture, at fixed values of temperature T and mole fraction of the liquid phase x (or the vapor phase y), the vapor pressure P and molar composition of the vapor phase y (or the liquid phase x), as well as the saturated liquid molar density and the saturated vapor molar density  are computed by solving a set of 4 algebraic equations (2 chemical potential and 2 pressure equalities). The binary cross-interaction parameters are determined by the minimization of the relative difference between literature data and theoretical values of vapor pressure and vapor mole composition:

$S_2={\displaystyle \sum }_{j=1}^N\left[{\left(\frac{P_j^{exp}-P_j^{cal}}{P_j^{exp}}\right)}^2+w_i{\left(\frac{y_j^{exp}-y_j^{cal}}{y_j^{exp}}\right)}^2\right]$ (44)

whereN is the number of experimental data used in the regression and w_i is a weighting coefficient for the relative deviations of the molar vapor composition. Regardless of the type of the experimental data, w_i = 0 when only (T,P,x) or (T,P,y) values are available and w_i = 1 when (T,P,x,y) values are available.

The optimized values of the binary cross-interaction parameters along with the absolute average deviations AAD for (1) vapor pressures (ΔP) and (2) molar compositions of the vapor phase are given in Table 4 for both thermodynamic models. As can be observed, the two equations of state correlate similarly the vapor pressure data. However, the GEOS (Δy = 0.6%) reproduces more accurately the molar composition data of the vapor phase than the PC-SAFT (Δy = 1.2%). In Figure 3 & Figure 4 are depicted the P-T curves of methylamine/water system at different values of the molar and mass fractions (Oldham or Dühring diagrams), respectively. As can be noted, both equations of state correlate comparably well the experimental data. The partial pressures of methylamine are estimated by the two investigated equations of state and compared to the experimental counterpart,⁴¹ as illustrated in Figure 5. Both models give globally similar predictions of partial pressures with a slight superiority to the GEOS equation of state.

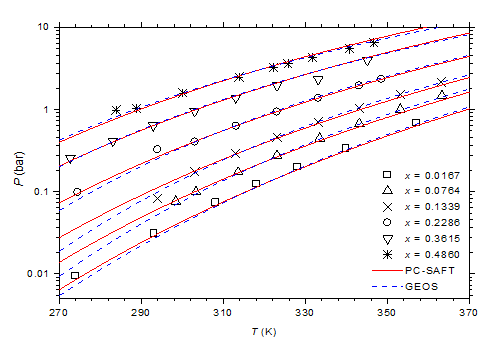
Figure 3 P-T-x diagram of methylamine/water mixture. Comparison of experimental data⁴¹ to calculated curves with GEOS and PC-SAFT models.

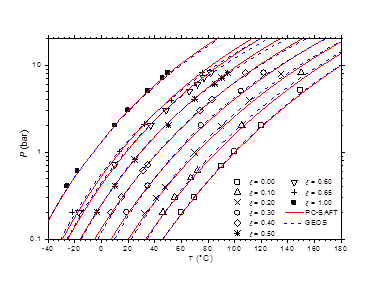
Figure 4 P-T-ξ diagram of methylamine/water mixture. Comparison of experimental data⁴⁰ to calculated values with GEOS and PC-SAFT models.

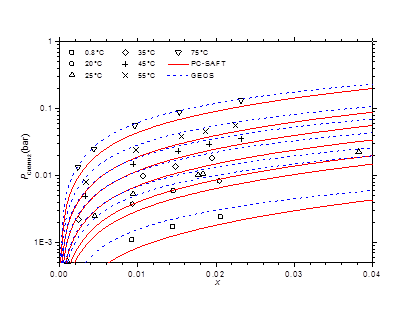
Figure 5 Partial pressures of methylamine via molar liquid fraction at different isotherms. Comparison of experimental data⁴¹ to theoretical values with GEOS and PC-SAFT.

The isobaric vapor-liquid phase equilibrium diagram at atmospheric pressure is illustrated in Figure 6. It is found that the theoretical curves of both EOS are very similar and reproduce with good accuracy the experimental dew point data in the entire composition range. However, the experimental bubble point data are offset from the calculated curves for molar liquid fractions lower than 0.2. The vapor-liquid phase equilibrium isotherms at different temperatures in the range of 303-383 K are illustrated in Figure 7-9. It can be concluded that the two models are similar and reproduce well the experimental data. A slight superiority is noted for the GEOS equation of state at high temperatures (near the critical temperature of methylamine) as can be seen for the isotherm 383.15 K for example. The enthalpy-composition-temperature (h-ξ-T) diagram of the saturated liquid phase of the methylamine/water system is represented in Figure 10. The predicted curves by the PC-SAFT and GEOS equations of state are confronted to literature data.⁴⁰ It can be observed that the two investigated models reproduce satisfactorily well the available experimental data in the literature. Finally, it can be concluded that both investigated EOS, GEOS and PC-SAFT, are in general similar and correlate with the same order of precision the experimental data of the methylamine/water binary mixture. It should be noted however that the available bibliographical data contain only a few data in the vicinity of the critical region where the capacity of each model to correlate the vapor-liquid phase behavior can be appreciated.

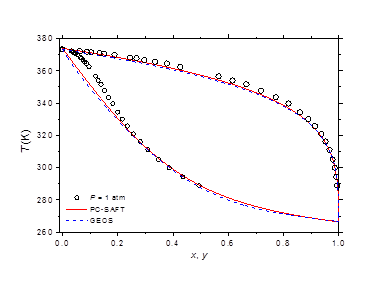
Figure 6 Vapor-liquid phase equilibria at atmospheric pressure of methylamine/water. Comparison of experimental data⁴⁹  to theoretical curves with GEOS and PC-SAFT models.

Figure 7 Phase equilibria of methylamine/water at 303.15, 313.15 and 323.15 K. Comparison of experimental data^50,51 to calculated curves with GEOS and PC-SAFT.

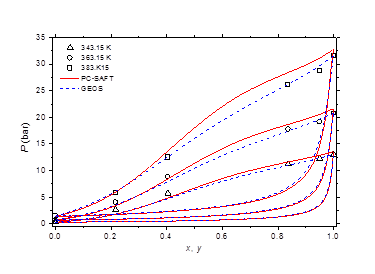
Figure 8 Phase equilibria of methylamine/water at 343.15, 363.15 and 383.15 K. Comparison of experimental data⁵⁰ to calculated curves with GEOS and PC-SAFT.

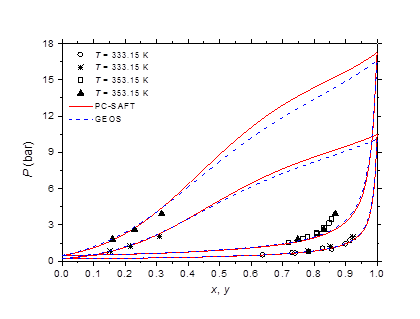
Figure 9 Phase behavior of methylamine/water at 333.15 and 353.15 K. Comparison of experimental data 51 to calculated curves with GEOS and PC-SAFT.

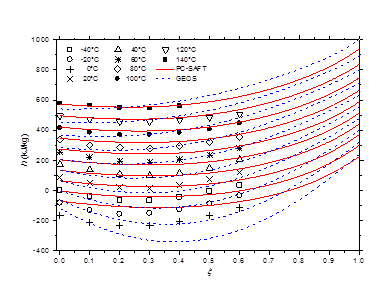
Figure 10 h-ξ-T diagram of saturated liquid phase for methylamine/water mixture. Comparison of literature data⁴⁰ to calculated curves by GEOS and PC-SAFT.

When the two investigated thermodynamic models for water-methylamine system property and liquid-vapor phase calculations are compared, it is found that

1. the performances of both equations of state in predicting the mixture properties are comparable;
2. GEOS is more accurate in reproducing and predicting the pure fluid properties and liquid-vapor phase equilibria of water and methylamine
3. GEOS is much easier in use and handier than the complex and more elaborated PC-SAFT equation of state. This issue is very important for the praxis, in particular if the equation of state is to be implemented in sophisticated flow-sheeting software.

For all these reasons, solely GEOS is retained in the following for the prediction of the properties of the binary mixtures of methylamine and water (Tables in Appendices C.1 and C2 and Figure 11 & Figure 12 representing the (h-T-ξ) and (s-T-ξ) diagrams of the saturated methylamine/water mixture up to very high temperature and pressure, respectively). It must be noted however that these curves and tables are deduced by extrapolation outside the domain of the available bibliographical data. Reasonable results are obtained, however the prediction accuracy in these areas is unknown. More experimental data are needed to assess the quality of the predicted properties, particularly in the critical and single-phase regions.

Figure 11 h-T-ξ diagram of saturated methylamine/water mixture plotted with GEOS.

Figure 12 s-T-ξ diagram of saturated methylamine/water mixture plotted with GEOS.

The vapor-liquid phase equilibria and thermodynamic properties of the methylamine/water binary mixture are modeled using two approaches, PC-SAFT equation of state and GEOS. A confrontation of the calculated and experimental data for pure fluids shows that the GEOS model is more accurate than the PC-SAFT equation in reproducing the vapor-liquid phase behavior and molar enthalpy of vaporization in the vicinity of the critical point of pure water. The binary cross-interaction parameters in the equations of state for the mixture are fitted from the few available vapor-liquid equilibria data. The comparison of the theoretical property predictions with experimental data leads to the conclusion that the two investigated equations of state are in general comparable in the calculation of the two-phase behavior of the methylamine/water system. However, the general cubic equation of state GEOS is more accurate in the neighborhood of the critical temperature of methylamine. This fact is probably due to the more accurate description of the vapor-liquid equilibrium of pure components near the critical region by GEOS. Further, a practical advantage of this equation of state is its simple mathematical structure, more tractable and easier to apply than the complex PC-SAFT EOS.

None.

The author declares that there is no conflict of interest.

1. Tyagi KP. Ammonia-salts vapor absorption refrigeration systems. Journal of Heat Recovery Systems. 1984;4(6)4:427–431.
2. Darwish NA, Al Hashimi SH, Al Mansoori AS. Performance analysis and evaluation of a commercial absorption–refrigeration water–ammonia (ARWA) system. International Journal of Refrigeration. 2008;31(7) 31:1214–1223.
3. Zavaleta Aguilar EW, Simões Moreira JR. Thermal design of a tray-type distillation column of an ammonia/water absorption refrigeration cycle. Applied Thermal Engineering. 2012;41(1):52–60.
4. Fernández Seara J, Sieres J. The importance of the ammonia purification process in ammonia–water absorption systems. Energy Conversion and Management. 2006;47(13-14):1975–1987.
5. Horuz I, Callander TM. Experimental investigation of a vapor absorption refrigeration system. International Journal of Refrigeration. 2004;27(1):10–16.
6. Eicker U, Pietruschka D. Design and performance of solar powered absorption cooling systems in office buildings. Energy and Buildings. 2009;41:81–91.
7. Engler M, Grossman G, Hellmann HM. Comparative simulation and investigation of ammonia-water: absorption cycles for heat pump applications. International Journal of Refrigeration. 1997;20(7):504–516.
8. Siddiqui MU, Said SA. A review of solar powered absorption systems. Renewable and Sustainable Energy Reviews. 2015;42:93–115.
9. Ullah K, Saidur R, Ping H, et al. A review of solar thermal refrigeration and cooling methods. Renewable and Sustainable Energy Reviews. 2013;24:499–513.
10. Wu W, Wang B, Shi W, et al. An overview of ammonia-based absorption chillers and heat pumps. Renewable and Sustainable Energy Reviews. 2014;31:681–707.
11. Steiu S, Salavera D, Bruno JC, et al. A basis for the development of new ammonia–water–sodium hydroxide absorption chillers. International Journal of Refrigeration. 2009;32(4):577–587.
12. Balamuru VG, Ibrahim OM, Barnett SM. Simulation of ternary ammonia–water–salt absorption refrigeration cycles. International Journal of Refrigeratio.2000;23(1):31–42.
13. Sun DW. Comparison of the performances of NH3-H2O, NH3-LiNO3 and NH3-NaSCN absorption refrigeration systems. Energy Conversion and Management. 1998;39(5-6):357–368.
14. Zhu L, Wang S, Gu J. Performance investigation of a thermal-driven refrigeration system. International Journal of Energy Research. 2008;32(10):939–949.
15. Chekir N, Mejbri Kh, Bellagi A. Simulation of an absorption chiller operating with alkane mixtures. International Journal of Refrigeration. 2006;29(10):469–475.
16. Kaushik SC, Kumar R. Comparative study of an absorber heat recovery cycle for solar refrigeration using NH3 refrigerant with liquid/solid absorbents. International Journal of Energy Research. 1987;11(1):123–132.
17. Ahachad M, Charia M, Bernatchou A. Study of an improved NH3/H2O solar absorption refrigerating machine in Rabat (Morocco). Solar Energy Materials and Solar Cells.1992;28(1):71–79.
18. Lazzarin RM, Gasparella A, Longo GA. Ammonia-water absorption machines for refrigeration: theoretical and real performances. International Journal of Refrigeration.1996;19(4):239–246.
19. Ghaddar NK, Shihab M, Bdeir F. Modeling and simulation of solar absorption system performance in Beirut. Renewable Energy. 1997;10(4):539–558.
20. Joudi KA, Lafta AH. Simulation of a simple absorption refrigeration system. Energy Conversion and Management. 2001;42(13):1575–1605.
21. Florides GA, Kalogirou SA, Tassou SA, et al. Modeling and simulation of an absorption solar cooling system for Cyprus. Solar Energy. 2002;72(1):43–51.
22. Barragán RM, Heard CL, Arellano VM, et al. Experimental performance of the water/calcium chloride system in a heat transformer. International Journal of Energy Research.1996; 20(8):651–661.
23. Ma X, Chen J, Li S, et al. Application of absorption heat transformer to recover waste heat from a synthetic rubber plant. Applied Thermal Engineering.2003;23(7):797–806.
24. Horuz I, Kurt B. Absorption heat transformers and an industrial application. Renewable Energy. 2010;35(10):2175–2181.
25. Rivera W, Huicochea A, Martínez H, et al. Exergy analysis of an experimental heat transformer for water purification. Energy. 2011;36(1):320–327.
26. Sekar S, Saravanan R. Experimental studies on absorption heat transformer coupled distillation system. Desalination. 2011;274(1-3):292–301.
27. Huicochea A, Rivera W, Martínez H, et al. Analysis of the behavior of an experimental absorption heat transformer for water purification for different mass flux rates in the generator. Applied Thermal Engineering. 2013;52(1):38–45.
28. Ibarra Bahena J, Romero RJ, Velazquez Avelar L, et al. Experimental thermodynamic evaluation for a single stage heat transformer prototype build with commercial PHEs. Applied Thermal Engineering. 2015;75:1262–1270.
29. Srikhirin P, Aphornratana S, Chungpaibulpatana S. A review of absorption refrigeration technologies. Renewable and Sustainable Energy Reviews. 2001;5(4):343–372.
30. Holmberg P, Berntsson T. Alternative working fluids in heat transformers. A shrae Transactions.1990:96.
31. Abed AM, Alghoul MA, Sopian K, et al. Enhancement aspects of single stage absorption cooling cycle: A detailed review. Renewable and Sustainable Energy Reviews. 2017;77(C):1010-1045.
32. Kilic M, Kaynakli O. Second law-based thermodynamic analysis of water-lithium bromide absorption refrigeration system. Energy. 2007;32(8):1505–1512.
33. Palacios Bereche R, Gonzales R, Nebra SA. Exergy calculation of lithium bromide–water solution and its application in the exergetic evaluation of absorption refrigeration systems LiBr-H2O. International Journal of Energy Research. 2012;36(2):166–181.
34. Misra RD, Sahoo PK, Sahoo S, et al. Thermo-economic optimization of a single effect water/LiBr vapor absorption refrigeration system. International Journal of Refrigeration. 2003;26(2):158–169.
35. Uemura T, Higuchi Y, Hasaba S. Studies on the monomethylamine–water absorption refrigerating machine. Refrigeration. 1967;42(471):2–13.
36. Tyagi KP. Comparison of binary mixtures for absorption refrigeration systems. Heat Recovery Systems.1983;3(5):421-429.
37. Pilatowsky I, Rxver W, Best R, et al. Thermodynamic design data for absorption heat pump systems operating on monomethylamine-water. Part III: Simultaneous cooling and heating. Heat Recovery Systems &CHP. 1995;15(6):583-589.
38. Pilatowsky I, Rivera W, Romero RJ. Thermodynamic analysis of monomethylamine–water solutions in a single-stage solar absorption refrigeration cycle at low generator temperatures. Solar Energy Materials & Solar Cells. 2001;70(3):287–300.
39. Pilatowsky I, Rivera W, Romero JR. Performance evaluation of a monomethylamine–water solar absorption refrigeration system for milk cooling purposes. Applied Thermal Engineering. 2004;24(7):1103–1115.
40. Romero RJ, Luis Guillen, Pilatowsky I. Monomethylamine–water vapor absorption refrigeration system. Applied Thermal Engineering. 2005;25:867–876.
41. Felsing WA, Thomas A. Vapor pressures and other physical constants of methylamine and methylamine solutions. Ind. Eng. Chem. 1929;21(12):1269-1272.
42. Felsing WA, Wohlford PH. The heats of solution of gaseous methylamine. Journal of American Chemical Society. 1932;54(4):1442–1445.
43. Mehl W, Ein Ubersichtsdiagramm log p-1/T fur das paar MethylaminWasser. Zeitsch f Ges. Kalte-Industrie. 1935;42(1):13–25.
44. Bonauguri EA, Bonfanti A, Gurdjian V. Gemische von CH2NH3 und H2O. La Thermotecnia.1954;5:53–78.
45. Ehmke HJ. Dissertation universitit essen. Forschungbericht des DKV No.1984.
46. Roberson JP, Lee CY, Squires RG, et al. Vapor pressure of ammonia and monomethylamine in solutions for absorption refrigeration systems. ASHRAE Trans. 1966;72(1):198–208.
47. Uemura T, Higuchi Y, Saito Y, et al. Studies on the Mono-Methylamine-Water Absorption Refrigerating Machine. Refrigeration. 1967;(42)471:2-13.
48. Pilatowsky I, Rivera W, Best R. State equations for monomethylamine–water solutions, derived from equilibrium diagrams. Non-published internal report. No. LES 94-0504-104. Mexico: Energy Solar Laboratory; IIM-UNAM; 1994. 110 p.
49. Gao D, Qiu Z, Yu S. Vapor-liquid equilibrium of three binary system: monomethylamine-H2O: dimethylamine-H2O and trimethylamine-H2O. Nanchang Daxue Xuebao. 2003;137(3):69–72.
50. Xu X, An L, Zheng G. Measurement of Vapor-Liquid Equilibrium Data for Products in Methanol Amination. Gaoxiao Huaxue Gongcheng Xuebao. 1995;9(1):97–105.
51. Stumm F, Heintz A, Lichtenthaler RN. Experimental data and modeling of vapor-liquid equilibria of the ternary system carbon dioxide + water + methylamine at 313, 333 and 353 K and pressures up to 0.4 MPa. Fluid Phase Equilibria. 1993;91(2):331–348.
52. Huang S, Radosz M. Equation of state for small, large, pollydisperse and associationg molecules. Industrial Engineering Chemical Research. 1990;29(11):2284–2294.
53. Huang S, Radosz M. Equation of state for small, large, pollydisperse and associationg molecules: extention to fluid mixtures. Industrial Engineering Chemical Research. 19991;30(8):1994–2005.
54. Gross J, Sadowski G. Application of the perturbed theory to a hard-chainreference fluid: an equation of state for square-well chains. Fluid Phase Equilibria. 2000;168(2):183–199.
55.  Gross J, Sadowski G. Perturbed-Chain SAFT: an equation of state based on a perturbation theory for chain molecules. Industrial Engineering Chemical Research. 20001;40(4):1244–1260.
56. Gross J, Sadowski G. Application of the perturbed-chain SAFT equation of state to associating systems, Industrial Engineering Chemical Research. 2002;41(22):5510–5515.
57. Gross J, Sadowski G. Modeling Polymer Systems Using the Perturbed-Chain Statistical Associating Fluid Theory Equation of State. Industrial Engineering Chemical Research. 2002;41(5):1084–1093.
58. Gross J, Spuhl O, Tumakaka F, et al. Modeling Copolymer Systems Using the Perturbed-Chain SAFT Equation of State. Industrial Engineering Chemical Research. 2003;42(6):1266–1274.
59. Mejbri KH, Thesis. Study of a single-pressure absorption refrigeration cycle: modeling, simulation and thermohydraulic design of a pilot installation for solar cold production. Tunisia: National Engineers School of Monastir; 2008. 6 p.
60. Mejbri Kh, Bellagi A. Équation d’état PC-SAFT appliquée aux fluides purs et aux mélanges binaires. Journal de la Société Chimique de Tunisie. 2005;7:125–138.
61. Mejbri Kh, Bellagi A. Modeling of the thermodynamic properties of the water/ammonia mixture by three different approaches. International Journal of Refrigeration. 2006;29(2):211–218.
62. Mejbri Kh, Taieb A, Bellagi A. Phase equilibria calculation of binary and ternary mixtures of associating fluids applying PC-SAFT equation of state. Journal of Supercritical Fluids. 2015;104(10):132–144.
63. Feroiu V, Geană D. Computation of vapor-liquid equilibrium in N2 + CO2 + CH4 system by a general cubic equation of state. Fluid Phase Equilibria. 1990;55(2):263–270.
64. Geană D, Feroiu V. Calculation of Joule-Thomson inversion curves from a general cubic equation of state. Fluid Phase Equilibria. 1992;77(1):121–132.
65. Geană D, Feroiu V. Thermodynamic properties of pure fluids using the GEOS3C equation of state. Fluid Phase Equilibria. 2000;174(1):51–68.
66. Feroiu V, Geană D. Volumetric and thermodynamic properties for pure refrigerants and refrigerant mixtures from cubic equations of state. Fluid Phase Equilibria. 2003;207(1-2):283–300.
67. Secuianu C, Feroiu V, Geană D. Phase behavior for carbon dioxide+ethanol system: Experimental measurements and modeling with a cubic equation of state. Journal of Supercritical Fluids. 2008;47(2):109–116.
68. Boggs p, Byrd R, Rogers J, et al. ODRPACK version 2.01 Software for weighted orthogonal distance regression, NIST. USA: Interagency Report; 1992. 120 p.
69. Shacham M. Numerical solution of constrained nonlinear equations. International Journal of Numerical Methods in Engineering. 1986;23(8):1455–1481.
70. NIST Standard Reference Database. In: Linstrom PJ, Mallard WG, editors. 2011.
71. Tyagi KP. Methylamine–sodium thiocyanate vapor absorption refrigeration. Heat Recovery Systems & CHP. 1992;12(3):283-287.
72. Vargraftik NB, Vinoradov YK, Yargin VS. Handbook of Physical Properties of Liquids and Gases, Pure Substances and Mixtures. Third Augmented and Revised Edition. New York: Begellhouse inc; 1996. 1359 p.
73. Perry RH, Green DW, Maloney JO. Perry’s Chemical Engineers’ Handbook. 7th edition. Newyork: McGraw-Hill; 1997. 2641 p.