International Journal of
eISSN: 2475-5559


Research Article Volume 5 Issue 1
Department of Mechanical Engineering, University of Lagos, Nigeria
Correspondence: MG Sobamowo, Department of Mechanical Engineering, University of Lagos, Akoka, Lagos, Nigeria
Received: January 01, 2020 | Published: July 14, 2020
Citation: Sobamowo MG, Yinusa AA, Aladenusi ST, et al. Magnetohydrodynamics natural convection of nanofluid flow over a vertical circular cone embedded in a porous medium and subjected to thermal radiation. Int J Petrochem Sci Eng 2020;5(1):22-38. DOI: 10.15406/ipcse.2020.05.00119
In this paper, magnetohydrodynamics natural convection of nanofluid flow over a vertical circular cone immersed in a porous medium under the influence of thermal radiation is investigated using multi-step differential transformation method. The accuracies of the analytical solutions are established through the verifications of the results of the present study with the results of the numerical solutions and the past studies. The approximate analytical solutions are used to examine the impacts of cone angle, flow medium porosity, magnetic field, nanoparticles volume-fraction and shape on the flow and heat transfer behaviours of the Copper (II) Oxide-water nanofluid. It is hoped that this study will enhance better understanding of flow process for the design of flow and heat transfer equipment.
Keywords: free convection, cone angle, porous medium, nanoparticle, magnetic field, multi-step differential transformation method
Symbols: β, volumetric extension coefficients; ρ, density of the fluid; µ,dynamic viscosity; η,similarity variable; λ, sphericity; Φ , volume fraction or concentration of the nanofluid; θ,dimensionless temperature
Subscript: f, fluid; s, solid; nf, nanofluid
There are various applications of free convection flow and heat transfer in aeronautics, reactor fluidization, glass-fiber production processes, aerodynamic, cooling of gas turbine rotor blades, drawing of a polymer sheet, food stuff processing, melt spinning, mechanical forming processes, cooling of metallic plates, wire and fiber coating, extrusion of plastic sheets, continuous casting, rolling, annealing, and tinning of copper wires. Since the quality of products in the processes depends considerably on the flow and heat transfer characteristics in the various applications, the analysis of fluid flow and heat transfer is very essential Earlier studies on free convections flow established its importance in science and engineering applications.1–11 However, the analyses of these studies are based on the approximations. Therefore, in some recent studies, improved approximated analyses of the flow and heat transfer models have been presented. Na & Habib12 adopted parameter differentiation method while Merkin13 presented the similarity solutions for free convection on a vertical plate. Merkin& Pop14 and Ali et al.,15 applied numerical methods for the flow process. In a very recent paper, Motsa et al.,16,17 utilized homotopy analysis method and spectral local linearization approach to analyze the free convection boundary layer flow with heat and mass transfer. Also, Ghotbi et al.,18 presented the analytical solutions to the free convection flow using the homotopy analysis method.
The simple procedures in the theory and applications of differential transformation method (DTM) have shown the effectiveness of the method in solving both linear and nonlinear equations. The method was introduced by Ζhou.19 In the free flow analysis, over a vertical surface, Yu & Chen20 and Kuo21,22 applied the method. However, it should be noted that the DTM solutions diverge for some differential equations that extremely have nonlinear behaviors or have boundary-conditions at infinity. This is because the series solution method is limited to small domain. Therefore, Rashidi et al.,23 applied DTM coupled with Padé-approximant technique to the flow problem. However, the Padé-approximant technique comes with large volume of calculations and computations. Therefore, another technique for an improved rate of convergence and the radius of convergence of power series solution is required. Among the newly developed techniques, is the multi-step differential transform method (MDTM). The method can be applied directly to nonlinear differential equations of infinite boundary conditions without the use of after-treatment techniques and domain transformation techniques.24–44
The previous studies on the problem under investigation are based on the flow of viscous fluid over a vertical surface without considering the effects of magnetic field and porosity of the flow medium. To the best of the author’s knowledge, a study on free convection flow of nanofluid over a vertical circular cone using multi-step differential transform method. Therefore, in this work, magnetohydrodynamics natural convection of nanofluid flow over a vertical circular cone immersed in a porous medium under the influence of thermal radiation is investigated using multi-step differential transformation method. The approximate analytical solutions are used to examine the impacts of cone angle, flow medium porosity, magnetic field, nanoparticles volume-fraction, shape and type on the flow and heat transfer behaviours of various nanofluids. Also, the accuracies of the analytical solutions are established through the verifications of the results with the results of the numerical solutions and the results in the past studies.
Problem formulation and mathematical analysis
Consider a free-convection flow of an incompressible electrically conducting nanofluid past a cone embedded in a porous medium which is inclined from the vertical with an acute angle γ measured in the clockwise direction and situated in an otherwise quiescent ambient fluid at temperature Tw as shown in Figure 1. A transverse magnetic field of strength Bo is applied normal to the inclined plate. The plate coincides with the plane y=0 and the flow being confined to y >0. Assuming that the flow in the laminar boundary layer is two-dimensional and steady, the equations for continuity and motion are given as
∂(ru)∂x+∂(rv)∂y=0 (1)
ρnf(u∂u∂x+v∂u∂y)=μnf∂2u∂y2+g(ρβ)nf(T−T∞)cosγ−σB2ou−μuK (2)
(ρcp)nf(u∂T∂x+v∂T∂y)=knf∂2T∂y2−∂qr∂y (3)
Assuming no slip conditions, the appropriate boundary conditions are given as
u=0, v=0, T=Ts at y=0 (4a)
u=0, T=Tw, at y→∞ (4b)
where the various physical and thermal properties in the Eq. (1-3) are given as
ρnf=ρf(1−ϕ)+ρsϕ (5a)
(ρcp)nf=(ρcp)f(1−ϕ)+(ρcp)sϕ (5b)
(ρβ)nf=(ρβ)f(1−ϕ)+(ρβ)sϕ (5c)
μnf=μf(1−ϕ)2.5 (5d)
knf=kf[ks+(m−1)kf−(m−1)ϕ(kf−ks)ks+(m−1)kf+ϕ(kf−ks)] (6)
σnf=σf[1+3{σsσf−1}ϕ{σsσf+2}ϕ−{σsσf−1}ϕ], (7)
The above model in Eq. (6) is Hamilton Crosser’s model. The “m” in the model represents the shape factor which its numerical values for different shapes are given in Table 1. It should be noted that the shape factor, m=3λ , where λ is the sphericity (the ratio of the surface area of the sphere and the surface area of the real particles with equal volumes). For sphericity of sphere, platelet, cylinder, laminar and brick are 1.000, 0.526, 0.625, 0.185 and 0.811, respectively. It should be noted that the Hamilton Crosser’s model becomes a Maxwell-Garnett’s model, when the shape factor of the nanoparticle, m=3. Tables 2&3 present the physical and thermal properties of the base fluid and the nanoparticles, respectively. SWCNTs mean single-walled carbon nanotubes.
|
Base fluid |
ρ (kg/m3) |
cp ( J/kgK) |
k (W/mK) |
|
Pure water |
997.1 |
4179 |
0.613 |
|
Ethylene Glycol |
1115 |
2430 |
0.253 |
|
Engine oil |
884 |
1910 |
0.144 |
|
Kerosene |
783 |
2010 |
0.145 |
Table 2 Physical and thermal properties of the base fluid37–44
|
Nanoparticles |
ρ (kg/m3) |
cp ( J/kgK) |
k (W/mK) |
|
Copper (Cu) |
8933 |
385 |
401 |
|
Aluminum oxide (Al2O3) |
3970 |
765 |
40 |
|
SWCNTs |
2600 |
42.5 |
6600 |
|
Silver (Ag) |
10500 |
235 |
429 |
|
Titanium dioxide (TiO2) |
4250 |
686.2 |
8.9538 |
|
Copper (II) Oxide (CuO) |
783 |
540 |
18 |
Table 3 Physical and thermal properties of nanoparticles37–44
However, the present study focusses on Copper (II) Oxide-water nanofluid.
r=xsinλ, (8)
Moreover γ is the half angle of the frustum cone. Because the boundary layer-thickness is small, the local radius to a point in the boundary layer r can be represented by the local radius of the cone.
Going back to Eq. (1), (2) and (3) and if one introduces a stream function, ψ(x,y) such that
ru=∂ψ∂y, rv=−∂ψ∂x, (9)
and use the following similarity and dimensionless variables
η=[ρ2f(gβf(Tw−T∞))4μ2fx]14y,ψ=4μfρf[ρ2f(gβf(Tw−T∞))x34μ2f]1/4f(η),
θ=T−T∞Tw−T∞,Pr=μfcpkf,
(10)
one arrives at fully coupled third and second orders ordinary differential equations
f‴(η)+(1−ϕ)2.5{[(1−ϕ)+ϕ(ρsρf)](3f(η)f″(η)−2(f′(η))2)+[(1−ϕ)+ϕ[(ρβ)s/(ρβ)f]]θ(η)cosγ}−(M2+1Da)f(η)=0 (11)
(1+43R)θ″+3[1[(1−ϕ)+ϕ[(ρCp)s/(ρCp)f]][ks+(m−1)kf−(m−1)ϕ(kf−ks)ks+(m−1)kf+ϕ(kf−ks)]]Prfθ′=0 (12)
and the boundary conditions as
f=0, f′=0, θ=1, when η=0 (13)
f′=0, θ=0, when η=∞ (14)
Basic concepts of differential transform method
The relatively new semi-analytical method, differential transformation method introduced by Zhou19 has proven proved very effective in providing highly accurate solutions to differential equations, difference equation, differential-difference equations, fractional differential equation, pantograph equation and integro-differential equation. Therefore, this method is applied to the present study. The basic definitions and the operational properties of the method are as follows
If u(t) is analytic in the domain T, then the function u(t) will be differentiated continuously with respect to time t.
dpu(t)dtp=φ(t,p) for all t∈T (15)
for t=ti , then φ(t,p)=φ(ti,p) , where p belongs to the set of non-negative integers, denoted as the p-domain. We can therefore write Eq. (15) as
U(p)=φ(ti,p)=[dpu(t)dtp]t=ti (16)
where Up is called the spectrum of u(t) at
Expressing u(t) in Taylor’s series as t=ti
u(t)=∞∑p[(t−ti)pp!] U(p) (17)
where Equ. (15) is the inverse of U(k) us symbol ‘D’ denoting the differential transformation process and combining (16) and (17), we have
u(t)=∞∑p=0[(t−ti)pp!] U(p)=D−1U(p) (18)
Basic concepts of multi-step differential transform method
The limitation of classical DTM is shown when is being used for solving differential equations with the boundary conditions at infinity i.e. the obtained series solution through the DTM for such equation with the boundary condition become divergent. Besides that, generally, power series solutions are not useful for large values of the independent variable. In order to overcome this shortcoming, the multi-step DTM is developed (Table 4). The basic concepts of the multi-step DTM for solving non-linear initial-value problem is presented as follows;
u(t,f,f′,...f(h))=0, (19)
subject to the initial conditions
f(k)(0)=ck, k=0,1,...h−1. (20)
Let [0, T] be the interval over which we want to find the solution of the initial value problem of Eq. (19). In actual application of the DTM, the approximate solution of the initial value problem of Eq. (19) can be expressed by the following finite series:
f(t)=M∑m=0amtm t∈[0, T]. (21)
The multi-step approach introduces a new idea for constructing the approximate solution. Assume that the interval [0, T] is divided into N subintervals [ti−1 , ti], i=1,2,...,N of equal step size H=T/N by using the nodes t=iH . The main idea of the multi-step DTM is as follows. First, we apply the DTM to Eq. (19) over the interval [0 , t1], we will obtain the following approximate solution,
f1(t)=K∑m=0a1mtm t∈[0 , t1], (22)
Using the initial conditions f(k)(0)=ck. For i≥2 and at each subinterval [ti−1 , ti] we will use the initial conditions f(k)i(ti−1)=f(k)i−1(ti−1) and apply the DTM to Eq. (19) over the interval [ti−1 , ti], where t0 in Eq. (15) is replaced by ti−1 . The process is repeated and generates a sequence of approximate solution, fi(t),i =1, 2,…,N for the solution f(t) ,
fi(t)=K∑m=0aim(t−ti−1)m, t∈[ti, ti+1], (23)
where M=K⋅N . In fact, the multi-step DTM assumes the following solution:
f(t){f1(t), t∈[0 , t1]... fi(t), t∈[ti , ti+1] ...fN(t), t∈[tN−1 , tN] (24)
which shows that there is a separate function for every sub domain.
Following the above definition, it could be stated that the multi-step DTM for every sub-domain is defined as
Fi(m)=Hmm![dmu(t)dtm]t=ti (25)
The inverse multi-step DTM is
fi(t)=∞∑m=0[(t−ti)mm!] Fi(m) (26)
The new algorithm, multi-step DTM is simple for computational performance for all values of H. It is easily observed that if the step size H=T , then the multi-step DTM reduces to the classical DTM. Using the operational properties of the differential transformation method, the differential transformation of the governing differential Eq. (10) is given as
(p+1)(p+2)(p+3)F(p+3)+(1−ϕ)2.5{α1[3p∑l=0(p−l+1)(p−l+2)F(l)F(p−l+2)−2p∑l=0(l+1)(p−l+1)F(l+1)F(p−l+1)]+α2Θ(p)cosγ−(M2+Da−1)F(p)}=0 (27)
Eq. (27) can be written as
F(p+3)=(1−ϕ)2.5(p+1)(p+2)(p+3){α1[2p∑l=0(l+1)(p−l+1)F(l+1)F(p−l+1)−3p∑l=0(p−l+1)(p−l+2)F(l)F(p−l+2)]−α2Θ(p)cosγ+(M2+Da−1)F(p)} (28)
For the Eq.(11), we have the recursive relation in differential transform domain as
(p+1)(p+2)Θ(p+2)+{3α3Prp∑l=0(l+1)Θ(l+1)F(p−l)}=0 (29)
which can be written as
Θ(p+2)=−3α3Pr(p+1)(p+2){p∑l=0(l+1)Θ(l+1)F(p−l)} (30)
where
α1=(1−ϕ)+ϕ(ρsρf)α2=[(1−ϕ)+ϕ[(ρβ)s/(ρβ)f]]α3=[1[(1−ϕ)+ϕ[(ρCp)s/(ρCp)f]][ks+(m−1)kf−(m−1)ϕ(kf−ks)ks+(m−1)kf+ϕ(kf−ks)]]
Also, recursive relation for the boundary conditions in Eq. (13) are
F(p)=0⇒F(0)=0, (p+1)F(p+1)=0 ⇒F(1)=0, θ(p)=1 ⇒θ(0)=1,F(2)=a, θ(1)=b, (31)
where a and b are unknown constants which will be found later.
It should be noted that the transformations which included “a” and “b” are established from values of f″(0)=a and θ′(0)=b
From Eq. (29), we have the following boundary conditions in differential transform domain
F[0]=0, F[1]=0, θ[0]=1, F[2]=a, θ[1]=b (32)
Using p=0, 1, 2, 3, 4, 5, 6, 7… in the above recursive relations in Eq. (29), we arrived at
F[3]=−16(1−ϕ)5/2α2cosγ
F[4]=−124(1−ϕ)5/2b α2cosγ
F[5]=a(2a(1−ϕ)5/2α1Da+M2Da+1)60Da
F[6]=−(DaM2+1)(1−ϕ)5/2α2cosγ720Da
F[7]=−(1−ϕ)5/2α2bcosγ(−40Da(1−ϕ)5/2Rdaα1−30(1−ϕ)5/2α1aDa+4DaM2Rd−18DaPraα3+3DaM2+4Rd+3)(15120+20160Rd)Da
F[8]=1(120960+161280Rd)Da2(6a+8Da2M4Rda+16DaM2Rda−144(1−ϕ)5/2α1a2Da+312Da2a3ϕ5α12−1560Da2a3ϕ4α12+3120Da2a3ϕ3α12−3120Da2a3ϕ2α12+1560Da2a3ϕα12−416Da2Rda3α12−192Da2M2(1−ϕ)5/2Rda2α1−15Da2(1−ϕ)5/2b(cosγ2)α1α22−9Da2Prb(cosγ2)α22α3+100Da2(1−ϕ)5/2Rdb(cosγ2)ϕα1α22−200Da2(1−ϕ)5/2Rdb(cosγ2)ϕ2α1α22−100Da2(1−ϕ)5/2Rdb(cosγ2)ϕ4α1α22+200Da2(1−ϕ)5/2Rdb(cosγ2)ϕ3α1α22+20Da2(1−ϕ)5/2Rdb(cosγ2)ϕ5α1α22−192Da(1−ϕ)5/2Rda2α1−144Da2M2(1−ϕ)5/2a2α1−4160Da2Rda3ϕ2α12+2080Da2Rda3ϕα12+4160Da2Rda3ϕ3α12+416Da2Rda3ϕ5α12−2080Da2Rda3ϕ4α12+8Rda+12DaM2a−312Da2a3α12+6Da2M4a−20Da2(1−ϕ)5/2Rdb(cosγ2)α1α22+75Da2(1−ϕ)5/2b(cosγ2)ϕα1α22+150Da2(1−ϕ)5/2b(cosγ2)ϕ3α1α22−150Da2(1−ϕ)5/2b(cosγ2)ϕ2α1α22+15Da2(1−ϕ)5/2b(cosγ2)ϕ5α1α22−75Da2(1−ϕ)5/2b(cosγ2)ϕ4α1α22+9Da2Prb(cosγ2)ϕ5α22α3−45Da2Prb(cosγ2)ϕ4α22α3+90Da2Prb(cosγ2)ϕ3α22α3−90Da2Prb(cosγ2)ϕ2α22α3+45Da2Prb(cosγ2)ϕα22α3)
F[9]=−(1−ϕ)5/2α2cosγ(1088640+1451520Rd)Da2(3−252(1−ϕ)5/2α1aDa+216Da2a2ϕ5α12−1080Da2a2ϕ4α12+2160Da2a2ϕ3α12−2160Da2a2ϕ2α12+1080Da2a2ϕα12−288Da2Rda2α12−15Da2b2cosγϕ5α1α2+75Da2b2cosγϕ4α1α2−150Da2b2cosγϕ3α1α2+150Da2b2cosγϕ2α1α2+20Da2Rdb2cosγα1α2−75Da2b2cosγϕα1α2−336Da2M2(1−ϕ)5/2Rdaα1+8DaM2Rd+200Da2Rdb2cosγϕ2α1α2+100Da2Rdb2cosγϕ4α1α2−1440Da2Rda2ϕ4α12−200Da2Rdb2cosγϕ3α1α2+9Da2(1−ϕ)5/2Prb2cosγα2α3−20Da2Rdb2cosγϕ5α1α2−100Da2Rdb2cosγϕα1α2−336Da(1−ϕ)5/2Rdaα1+288Da2Rda2ϕ5α12+15Da2b2cosγα1α2−252Da2M2(1−ϕ)5/2aα1−2880Da2Rda2ϕ2α12+1440Da2Rda2ϕα12+2880Da2Rda2ϕ3α12+6M2Da+3Da2M4+4Da2M4Rd−216Da2a2α12+4Rd)
F[10]=−(1−ϕ)5/2α2cosy3628800(3+4Rd)2Da2(−77760Da2Rda2bϕα12+9b+5832Da2a2bα12+16Da2M4Rd2b+24Da2M4Rdb+32DaM2Rd2b+48DaM2Rdb+378Dacosγα1α2−378Da2M2cosγϕ5α1α2+1890Da2M2cosγϕ4α1α2−672DaRd2cosγϕ5α1α2−3780Da2M2cosγϕ3α1α2+3360DaRd2cosγϕ4α1α2−1008DaRdcosγϕ5α1α2+672Da2M2Rd2cosγα1α2−6720DaRd2cosγϕ3α1α2+5040DaRdcosγϕ4α1α2−10368Da2Rd2a2bϕ5α12+51840Da2Rd2a2bϕ4α12−15552Da2Rda2bϕ5α12−103680Da2Rd2a2bϕ3α12+77760Da2Rda2bϕ4α12+103680Da2Rd2a2bϕ2α12−155520Da2Rda2bϕ3α12−51840Da2Rd2a2bϕα12+155520Da2Rda2bϕ2α12+5328Da2(1−ϕ)5/2PrRda2bα1α3+3780Dacosγϕ2α1α2+672DaRd2cosγα1α2+378Da2M2cosγα1α2+3360Da2M2Rd2cosγϕ4α1α2−3780Dacosγϕ3α1α2+1890Dacosγϕ4α1α2+3240Da22Pra2bα32−378Dacosγϕ5α1α2+10080Da2M2Rdcosγϕ2α1α2−3360Da2M2Rd2cosγϕα1α2−10080Da2M2Rdcosγϕ3α1α2+6720Da2M2Rd2cosγϕ2α1α2+5040Da2M2Rdcosγϕ4α1α2−6720Da2M2Rd2cosγϕ3α1α2−1008Da2M2Rdcosγϕ5α1α2−3408Da(1−ϕ)5/2Rdabα1+3780Da2M2cosγϕ2α1α2−2272Da(1−ϕ)5/2Rd2abα1−1278Da2M2(1−ϕ)5/2abα1−5040DaRdcosγϕα1α2−144DaPrRdabα3+10080DaRdcosγϕ2α1α2−3360DaRd2cosγϕα1α2−10080DaRdcosγϕ3α1α2+6720DaRd2cosγϕ2α1α2−1890Da2M2cosγϕα1α2+1008Da2M2Rdcosγα1α2−672Da2M2Rd2cosγϕ5α1α2−108Da2M2Prabα3+9Da2M4b+18DaM2b−1278Da(1−ϕ)5/2abα1−108DaPrabα3+1008DaRdcosγα1α2−1890Dacosγϕα1α2+58320Da2a2bϕ2α12−29160Da2a2bϕα12+29160Da2a2bϕ4α12−58320Da2a2bϕ3α12−5832Da2a2bϕ5α12+10368Da2Rd2a2bα12+15552Da2Rda2bα12+16Rd2b+24Rdb−5040Da2M2Rdcosγϕα1α2−144Da2M2PrRdabα3+3996Da2(1−ϕ)5/2Pra2bα1α3−3408Da2M2(1−ϕ)5/2Rdabα1−2272Da2M2(1−ϕ)5/2Rd2abα1)
In the same manner, the expressions for F [11], F[12], F[13], F[14], F[15] are found but they are too large to be included in this paper.
Also, using p=0, 1, 2, 3… in the above recursive relations in Eq. (30), we arrived at following solutions
Θ[2]=0
Θ[3]=0
Θ[4]=−34(α3Pra b3+4Rd)
Θ[5]=3α3Pr(1−ϕ)5/2b α2cosγ120+160Rd
Θ[6]=α3Prb2(1−ϕ)5/2α2cosγ240+320Rd
Θ[7]=−α3Prba(3+8Da(1−ϕ)5/2Rdaα1+6(1−ϕ)5/2α1aDa+4DaM2Rd−180DaPraα3+3DaM2+4Rd)280(3+4Rd)2Da
Θ[8]=α3Pr(1−ϕ)5/2b α2cosγ(4DaM2Rd−630DaPraα3+3DaM2+4Rd+3)4480(3+4Rd)2Da
Θ[9]=α3Prbα2cosγ40320(3+4Rd)2Da(4DaM2(1−ϕ)5/2Rdb−1026α3Prba(1−ϕ)5/2Da−315DaPrcosγϕ5α2α3+40DaRdabϕ5α1+3DaM2(1−ϕ)5/2b+1575DaPrcosγϕ4α2α3−200DaRdabϕ4α1+30Daabϕ5α1+150Daabϕα1−30Daabα1−3150DaPrcosγϕ3α2α3+400DaRdabϕ3α1−150Daabϕ4α1+3150DaPrcosγϕ2α2α3−400DaRdabϕ2α1+300Daabϕ3α1+4(1−ϕ)5/2Rdb−1575DaPrcosγϕα2α3+200DaRdabϕα1−300Daabϕ2α1+3b(1−ϕ)5/2+315α3Prα2cosγDa−40DaRdabα1)
Θ[10]=−α3Prb403200(3+4Rd)3Da2(−1152Da2M2(1−ϕ)5/2Rda2α1−450Da2(1−ϕ)5/2b(cosγ2)ϕ2α1α22+18a−9072α3Pra2Da+48Da2M4Rda+96DaM2Rda−432(1−ϕ)5/2α1a2Da+936Da2a3ϕ5α12−4680Da2a3ϕ4α12+9360Da2a3ϕ3α12−9360Da2a3ϕ2α12+4680Da2a3ϕα12−45Da2(1−ϕ)5/2b(cosγ2)α1α22−12096Da2M2PrRda2α3−18144Da2(1−ϕ)5/2Pra3α1α3−768Da2M2(1−ϕ)5/2Rd2a2α1−12096DaPrRda2α3−9072Da2M2Pra2α3+450Da2(1−ϕ)5/2b(cosγ2)ϕ3α1α22−225Da2(1−ϕ)5/2b(cosγ2)ϕ4α1α22+45Da2(1−ϕ)5/2b(cosγ2)ϕ5α1α22+3429Da2Prb(cosγ2)ϕ5α22α3+34290Da2Prb(cosγ2)ϕ3α22α3−34290Da2Prb(cosγ2)ϕ2α22α3−80Da2(1−ϕ)5/2Rd2b(cosγ2)α1α22−4572Da2PrRdb(cosγ2)α22α3−17145Da2Prb(cosγ2)ϕ4α22α3−120Da2(1−ϕ)5/2Rdb(cosγ2)α1α22−24192Da2(1−ϕ)5/2PrRda3α1α3+225Da2(1−ϕ)5/2b(cosγ2)ϕα1α22+600Da2(1−ϕ)5/2Rdb(cosγ2)ϕα1α22−1200Da2(1−ϕ)5/2Rdb(cosγ2)ϕ2α1α22+1200Da2(1−ϕ)5/2Rdb(cosγ2)ϕ3α1α22−600Da2(1−ϕ)5/2Rdb(cosγ2)ϕ4α1α22+120Da2(1−ϕ)5/2Rdb(cosγ2)ϕ5α1α22+32Rd2a+18Da2M4a−1152Da(1−ϕ)5/2Rda2α1−432Da2M2(1−ϕ)5/2a2α1+12480Da2Rda3ϕα12−936Da2a3α12−3429Da2Prb(cosγ2)α22α3+17145Da2Prb(cosγ2)ϕα22α3+400Da2(1−ϕ)5/2Rd2b(cosγ2)ϕα1α22+36DaM2a+800Da2(1−ϕ)5/2Rd2b(cosγ2)ϕ3α1α22−800Da2(1−ϕ)5/2Rd2b(cosγ2)ϕ2α1α22+80Da2(1−ϕ)5/2Rd2b(cosγ2)ϕ5α1α22−400Da2(1−ϕ)5/2Rd2b(cosγ2)ϕ4α1α22−45720Da2PrRdb(cosγ2)ϕ2α22α3+22860Da2PrRdb(cosγ2)ϕα22α3+4572Da2PrRdb(cosγ2)ϕ5α22α3−22860Da2PrRdb(cosγ2)ϕ4α22α3+45720Da2PrRdb(cosγ2)ϕ3α22α3−24960Da2Rda3ϕ2α12+24960Da2Rda3ϕ3α12−12480Da2Rda3ϕ4α12+2496Da2Rda3ϕ5α12+8320Da2Rd2a3ϕα12+181440Da22Pra3α32+48Rda +16640Da2Rd2a3ϕ3α12−16640Da2Rd2a3ϕ2α12−8320Da2Rd2a3ϕ4α12−768Da(1−ϕ)5/2Rd2a2α1+1664Da2Rd2a3ϕ5α12−2496Da2Rda3α12+64DaM2Rd2a+32Da2M4Rd2a−1664Da2Rd2a3α12)
In the same manner, the expressions for Θ [11], Θ[12], Θ[13], Θ[14], Θ[15]… are found but they are too large to be included in this paper
From the definition in Eq. (18), the solutions of Eqs. (10) and (11) are given as
f(η)=F[0]+ηF[1]+η2F[2]+η3F[3]++η4F[4]+η5F[5] +η6F[6]+η7F[7]+η8F[8]+η9F[9]++η10F[10]+... (33)
θ(η)=Θ[0]+ηΘ[1]+η2Θ[2]+η3Θ[3]++η4Θ[4]+η5Θ[5] +η6Θ[6]+η7Θ[7]+η8Θ[8]+η9Θ[9]++η10Θ[10]+... (34)
Now, consider similar fully coupled third and second orders ordinary differential equations presented in Eqs. (11) and (12), but at this time, we take a=1 and b=1
g‴(η)+(1−ϕ)2.5{α1(3g(η)g″(η)−2(f′(η))2)+α2ϑ(η)cosγ−(M2+Da−1)g(η)}=0 (35)
ϑ″(η)+3α3Prg(η)ϑ′(η)=0 (36)
With initial conditions as
& g=0, g′=0, g″=1, ϑ=1, ϑ′=1 when η=0 nbsp; (37)
Following the similar solution procedures of Eqs. (10) and (11), the solutions of Eqs. (35) and (36) are
g(η)=G[0]+ηG[1]+η2G[2]+η3G[3]++η4G[4]+ηGF[5] +η6G[6]+η7G[7]+η8G[8]+η9G[9]++η10G[10]+... (38)
ϑ(η)=Φ[0]+ηΦ[1]+η2Φ[2]+η3Φ[3]++η4Φ[4]+η5Φ[5] +η6Φ[6]+η7Φ[7]+η8Φ[8]+η9Φ[9]++η10Φ[10]+.. (39)
where
G[0]=0, G[1]=0, ,G[2]=12, θ[0]=1, θ[1]=1
G[3]=−16(1−ϕ)5/2α2cosγ
G[4]=−124(1−ϕ)5/2α2cosγ
G[5]=((1−ϕ)5/2α1Da+M2Da+1)120Da
G[6]=−(DaM2+1)(1−ϕ)5/2α2cosγ720Da
G[7]=−(1−ϕ)5/2α2cosγ(−20Da(1−ϕ)5/2Rdα1−15(1−ϕ)5/2α1Da+4DaM2Rd−9DaPrα3+3DaM2+4Rd+3)(15120+20160Rd)Da
G[8]=1(120960+161280Rd)Da2(3+4Da2M4Rd+8DaM2Rd−36(1−ϕ)5/2α1Da+78Da2a3ϕ5α12−195Da2ϕ4α12+390Da2ϕ3α12−390Da2ϕ2α12+195Da2ϕα12−52Da2Rdα12−48Da2M2(1−ϕ)5/2Rdα1−15Da2(1−ϕ)5/2(cosγ)2α1α22−9Da2Pr(cosγ)2α22α3+100Da2(1−ϕ)5/2Rd(cosγ)2ϕα1α22−200Da2(1−ϕ)5/2Rd(cosγ)2ϕ2α1α22−100Da2(1−ϕ)5/2Rd(cosγ)2ϕ4α1α22+200Da2(1−ϕ)5/2Rd(cosγ)2ϕ3α1α22+20Da2(1−ϕ)5/2Rd(cosγ)2ϕ5α1α22−48Da(1−ϕ)5/2Rdα1−36Da2M2(1−ϕ)5/2α1−520Da2Rdϕ2α12+260Da2Rdϕα12+520Da2Rdϕ3α12+52Da2Rdϕ5α12−260Da2Rdϕ4α12+4Rd+6DaM2−39Da2α12+3Da2M4−20Da2(1−ϕ)5/2Rd(cosγ)2α1α22+75Da2(1−ϕ)5/2(cosγ)2ϕα1α22+150Da2(1−ϕ)5/2(cosγ)2ϕ3α1α22−150Da2(1−ϕ)5/2(cosγ)2ϕ2α1α22+15Da2(1−ϕ)5/2(cosγ)2ϕ5α1α22−75Da2(1−ϕ)5/2(cosγ)2ϕ4α1α22+9Da2Pr(cosγ)2ϕ5α22α3−45Da2Pr(cosγ)2ϕ4α22α3+90Da2Pr(cosγ)2ϕ3α22α3−90Da2Pr(cosγ)2ϕ2α22α3+45Da2Pr(cosγ)2ϕα22α3)
G[9]=−(1−ϕ)5/2α2cosγ(1088640+1451520Rd)Da2(3−126(1−ϕ)5/2α1Da+54Da2ϕ5α12−270Da2ϕ4α12+540Da2ϕ3α12−540Da2ϕ2α12+270Da2ϕα12−72Da2Rdα12−15Da2cosγϕ5α1α2+75Da2cosγϕ4α1α2−150Da2cosγϕ3α1α2+150Da2cosγϕ2α1α2+20Da2Rdcosγα1α2−75Da2cosyϕα1α2−168Da2M2(1−ϕ)5/2Rda1+4DaM2Rd+200Da2Rdcosγϕ2α1α2+100Da2Rdcosγϕ4α1α2−360Da2Rdϕ4α12−200Da2Rdcosγϕ3α1α2+9Da2(1−ϕ)5/2Prcosγα2α3−20Da2Rdcosγϕ5α1α2−100Da2Rdcosγϕα1α2−168Da(1−ϕ)5/2Rda1+72Da2Rdϕ5α12+15Da2cosγα1α2−126Da2M2(1−ϕ)5/2α1−720Da2Rdϕ2α12+360Da2Rdϕ2α12+720Da2Rdϕ3α12+6M2Da+3Da2M4+4Da2M4Rd−54Da2α12+4Rd)
G[10]=−(1−ϕ)5/2α2cosy3628800(3+4Rd)2Da2(−19440Da2Rdϕα12+9b+1458Da2α12+16Da2M4Rd2+24Da2M4Rd+32DaM2Rd2+48DaM2Rd+378Dacosγα1α2−378Da2M2cosγϕ5α1α2+1890Da2M2cosγϕ4α1α2−672DaRd2cosγϕ5α1α2−3780Da2M2cosγϕ3α1α2+3360DaRd2cosγϕ4α1α2−1008DaRdcosγϕ5α1α2+672Da2M2Rd2cosγα1α2−6720DaRd2cosγϕ3α1α2+5040DaRdcosγϕ4α1α2−2592Da2Rd2ϕ5α12+12960Da2Rd2ϕ4α12−3888Da2Rdϕ5α12−25920Da2Rd2ϕ3α12+77760Da2Rda2ϕ4α12+25920Da2Rd2α12−77760Da2Rda2α12−12960Da2Rd2ϕα12+38880Da2Rdϕ2α12+1332Da2(1−ϕ)5/2PrRdα1α3+3780Dacosγϕ2α1α2+672DaRd2cosγα1α2+378Da2M2cosγα1α2+3360Da2M2Rd2cosγϕ4α1α2−3780Dacosγϕ3α1α2+1890Dacosγϕ4α1α2+810Da22Prbα32−378Dacosγϕ5α1α2+10080Da2M2Rdcosγϕ2α1α2−3360Da2M2Rd2cosyϕα1α2−10080Da2M2Rdcosγϕ3α1α2+6720Da2M2Rd2cosγϕ2α1α2+5040Da2M2Rdcosγϕ4α1α2−6720Da2M2Rd2cosγϕ3α1α2−1008Da2M2Rdcosγϕ5α1α2−1704Da(1−ϕ)5/2Rdα1+3780Da2M2cosγϕ2α1α2−1138Da(1−ϕ)5/2Rd2α1−639Da2M2(1−ϕ)5/2α1−5040DaRdcosγϕα1α2−72DaPrRdα3+10080DaRdcosγϕ2α1α2−3360DaRd2cosγϕα1α2−10080DaRdcosγϕ3α1α2+6720DaRd2cosγϕ2α1α2−1890Da2M2cosγϕα1α2+1008Da2M2Rdcosγα1α2−672Da2M2Rd2cosγϕ5α1α2−54Da2M2Prα3+9Da2M4+18DaM2−639Da(1−ϕ)5/2α1−54DaPrα3+1008DaRdcosγα1α2−1890Dacosγϕα1α2+14580Da2bϕ2α12−7290Da2ϕα12+7290Da2ϕ4α12−14580Da2bϕ3α12−1458Da2ϕ5α12+2592Da2Rd2α12+3888Da2Rdα12+16Rd2+24Rd−5040Da2M2Rdcosγϕα1α2−72Da2M2PrRdα3+999Da2(1−ϕ)5/2Prα1α3−1704Da2M2(1−ϕ)5/2Rdα1−1388Da2M2(1−ϕ)5/2Rd2α1)
Similarly
Φ[2]=0
Φ[3]=0
Φ[4]=−38(α3Pr3+4Rd)
Φ[5]=3α3Pr(1−ϕ)5/2 α2cosγ120+160Rd
Φ[6]=α3Pr(1−ϕ)5/2α2cosγ240+320Rd
Φ[7]=−α3Pr(3+4Da(1−ϕ)5/2Rdα1+3(1−ϕ)5/2α1Da+4DaM2Rd−90DaPrα3+3DaM2+4Rd)560(3+4Rd)2Da
Φ[8]=α3Pr(1−ϕ)5/2 α2cosy(4DaM2Rd−315DaPrα3+3DaM2+4Rd+3)4480(3+4Rd)2Da
Φ[9]=α3Prα2cosγ40320(3+4Rd)2Da(4DaM2(1−ϕ)5/2Rd−516α3Prb(1−ϕ)5/2Da−315DaPrcosγϕ5α2α3+20DaRdϕ5α1+3DaM2(1−ϕ)5/2+1575DaPrcosγϕ4α2α3−100DaRdϕ4α1+15Daϕ5α1+75Daϕα1−15Daα1−3150DaPrcosγϕ3α2α3+200DaRdϕ3α1−75Daϕ4α1+3150DaPrcosγϕ2α2α3−200DaRdϕ2α1+150Daϕ3α1+4(1−ϕ)5/2Rd−1575DaPrcosγϕα2α3+100DaRdϕα1−150Daϕ2α1+3(1−ϕ)5/2+315α3Prα2cosγDa−20DaRdα1)
Φ[10]=−α3Prb403200(3+4Rd)3Da2(−1152Da2M2(1−ϕ)5/2Rda2α1−450Da2(1−ϕ)5/2(cosγ2)ϕ2α1α22+9−2268α3PrDa+24Da2M4Rd+48DaM2Rd−108(1−ϕ)5/2α1Da+117Da2ϕ5α12−585Da2ϕ4α12+1170Da2ϕ3α12−1170Da2ϕ2α12+585Da2ϕα12−45Da2(1−ϕ)5/2(cosγ2)α1α22−3024Da2M2PrRdα3−2268Da2(1−ϕ)5/2Prα1α3−192Da2M2(1−ϕ)5/2Rd2α1−3024DaPrRdα3−2268Da2M2Prα3+450Da2(1−ϕ)5/2(cosγ2)ϕ3α1α22−225Da2(1−ϕ)5/2(cosγ2)ϕ4α1α22+45Da2(1−ϕ)5/2(cosγ2)ϕ5α1α22+3429Da2Pr(cosγ2)ϕ5α22α3+34290Da2Pr(cosγ2)ϕ3α22α3−34290Da2Pr(cosγ2)ϕ2α22α3−80Da2(1−ϕ)5/2Rd2(cosy)2α1α22−4572Da2PrRd(cosγ2)α22α3−17145Da2Pr(cosγ2)ϕ4α22α3−120Da2(1−ϕ)5/2Rd(cosγ2)α1α22−3024Da2(1−ϕ)5/2PrRdα1α3+225Da2(1−ϕ)5/2(cosγ2)ϕα1α22+600Da2(1−ϕ)5/2Rd(cosγ2)ϕα1α22−1200Da2(1−ϕ)5/2Rd(cosγ2)ϕ2α1α22+1200Da2(1−ϕ)5/2Rd(cosγ2)ϕ3α1α22−600Da2(1−ϕ)5/2Rd(cosγ2)ϕ4α1α22+120Da2(1−ϕ)5/2Rd(cosγ2)ϕ5α1α22+16Rd2+9Da2M4−288Da(1−ϕ)5/2Rdα1−108Da2M2(1−ϕ)5/2α1+1560Da2Rdϕα12−117Da2α12−3429Da2Pr(cosγ2)α22α3+17145Da2Pr(cosγ2)ϕα22α3+400Da2(1−ϕ)5/2Rd2(cosγ2)ϕα1α22+36DaM2a+800Da2(1−ϕ)5/2Rd2(cosγ2)ϕ3α1α22−800Da2(1−ϕ)5/2Rd2(cosγ2)ϕ2α1α22+80Da2(1−ϕ)5/2Rd2(cosγ2)ϕ5α1α22−400Da2(1−ϕ)5/2Rd2(cosγ2)ϕ4α1α22−45720Da2PrRdb(cosγ2)ϕ2α22α3+22860Da2PrRdbcosy2ϕα22α3+4572Da2PrRdbcosy2ϕ5α22α3−22860Da2PrRd(cosγ2)ϕ4α22α3+45720Da2PrRd(cosγ2)ϕ3α22α3−3120Da2Rdϕ2α12+3120Da2Rdϕ3α12−1560Da2Rdϕ4α12+312Da2Rdϕ5α12+1040Da2Rd2ϕα12+22680Da2Pr2a3α32+24Rd +2080Da2Rd2ϕ3α12−2080Da2Rd2a3ϕ2α12−1040Da2Rd2ϕ4α12−192Da(1−ϕ)5/2Rd2α1+208Da2Rd2ϕ5α12−312Da2Rdα12+32DaM2Rd2+16Da2M4Rd2−208Da2Rd2α12)
The functions in Eq. (33) and (34) and that in Eq. (38) and (39) have relations as follows:
f(η)=akg(aqη) →f′(η)=ak+qg′(aqη)→f′(∞)=ak+qg′(∞) (40)
and
θ(η)=brϑ(bsη) →θ(∞)=brϑ(∞) (41)
From Eq. (12), f′(∞)=0 and θ(∞)=0
Since a≠0 and b≠0→g′(∞)=0 and ϑ(∞)=0
Applying multi-step DTM
To solve the boundary layer problems, the domain [0,∞) is replaced by [0, η ͚). But η ͚ should be great enough that the solution is not dependent on. The solution domain should be divided to N equal parts (H= η ͚ /N). So, we have
g‴i(ηi)+(1−ϕ)2.5{[(1−ϕ)+ϕ(ρsρf)](3gi(ηi)g″i(ηi)−2(g′i(ηi))2)+[(1−ϕ)+ϕ[(ρβ)s/(ρβ)f]]ϑi(ηi)cosγ−(M2+Da−1)gi(ηi)}=0 (42)
(i−1)H≤ηi<iH, for i≤i≤N
ϑ″i(ηi)+3[1[(1−ϕ)+ϕ[(ρCp)s/(ρCp)f]][ks+(m−1)kf−(m−1)ϕ(kf−ks)ks+(m−1)kf+ϕ(kf−ks)]]Prgi(ηi)ϑ′i(ηi)=0 (43)
(i−1)H≤ηi<iH, for i≤i≤N
Applying multi-step DTM on Eq. (42) and Eq. (43)
Gi(p+3)=(1−ϕ)2.5H3(p+1)(p+2)(p+3){α1[2p∑l=0(l+1)HGi(l+1)(p−l+1)HGi(p−l+1)−3p∑l=0Gi(l)(p−l+1)(p−l+2)H2Gi(p−l+2)]−α2ϑi(p)cosγ−(M2+Da−1)Gi(p)} (44)
for i≤i≤N
ϑi(p+2)=−3H2Pr(p+1)(p+2){α3p∑l=0(l+1)Hϑi(l+1)Gi(p−l)} (45)
for i≤i≤N
The initial conditions for the problem are considered for the first sub domain (i =1). Followng Eq. (24), the differential transform for the initial conditions for Eq. (35) and (36) and for Eqs. (44) and (45) are
G1(0)=g1(0)=0, G1(1)=Hg′1(0)=0, G1(2)=H22g″1=H22, Ψ1(0)=ϑ1(0)=1, Ψ1(1)=Hϑ′(0)=H (46)
The boundary conditions of each subdomain are continuity of the
gi(ηi), g′i(ηi), g″(ηi), ϑ(ηi), and ϑ′(ηi) (47)
These boundary conditions can be obtained from Eq. (26):
gi(ηi+1)=m∑k=0Gi(k)gi+1(ηi+1)=Gi+1(0)→Gi+1(0)=m∑k=0Gi(k) (48a)
g′i(ηi+1)=m∑k=1kHGi(k)g′i(ηi+1)=Gi+1(1)H→Gi+1(1)=m∑k=1kGi(k) (48b)
g″i(ηi+1)=m∑k=2k(k−1)H2Gi(k)g″i(ηi+1)=2Gi+1(2)H2→Gi+1(2)=12m∑k=1k(k−1)Gi(k) (48c)
ϑi(ηi+1)=m∑k=0Ψi(k)ϑi+1(ηi+1)=Ψi+1(0)→Ψi+1(0)=m∑k=0Ψi(k) (49a)
ϑ′i(ηi+1)=m∑k=1kHΨi(k)ϑ′i(ηi+1)=Ψi+1(1)H→Ψi+1(1)=m∑k=1kΨi(k) (49b)
The values of the g′(η∞) and ϑ(η∞) can be calculated by differentiating from Eq. (24)
g′i(∞)≃g′i(η∞)=g′i(ηN+1)=m∑k=1kHGN(k)ϑi(∞)≃ϑi(η∞)=ϑi(ηN+1)=m∑k=0ΨN(k) (50)
Now, Eq. (11) and (12) are solved with a similar process like Eqs. (35) and (36) using multi-step DTM. The only difference is that the condition f″(0)=a is replaced by the condition g″(0)=1
It should be noted as mentioned previously that the unknown parameters “a” and “b” in the solutions are unknown constants. The infinite boundary conditions i.e. η→∞, f′=0, θ=0 are applied. The resulting simultaneous equations are solved to obtain the values of “a” and “b” for the respective values of the physical and thermal properties of the nanofluids under considerations (Figures 1–4).

Figure 2 (a) Effects of cone angle on the velocity profile, (b) Effects of cone angle on temperature profile.
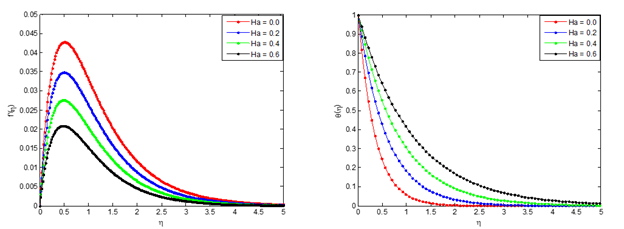
Figure 3 (a) Effects of magnetic field on the velocity profile, (b) Effects of magnetic field on temperature profile.
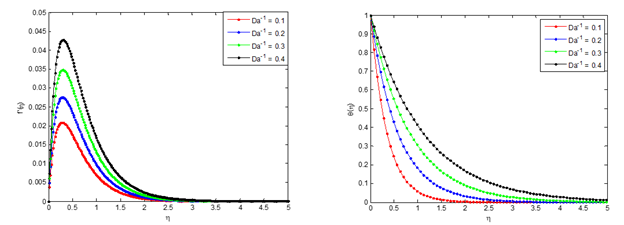
Figure 4 (a) Effects of flow medium porosity on the velocity profile, (b) Effects of flow medium porosity on temperature profile.
Flow and heat transfer parameters
The determinations of other physically important quantities such as shear stress, drag, heat transfer rate and heat transfer coefficient) associated with the free convection flow and heat transfer problem are very important in the design of equipment. Therefore, in this analysis physically important quantities are computed. The local heat transfer coefficient at the surface of the vertical plate can be obtained from
Fluid flow parameter
Skin friction coefficient
cf=τwρnfu2=μnf∂u∂y|y=0ρnfu2=μnf(∂u∂η⋅∂η∂y)|y=0ρnfu2 (51)
The dimensionless form of the skin friction coefficient,
cf(Rex)1/2=f″(0)(1−ϕ)2.5cf(Rex)1/2τw(4Gr3x)1/4(νμ)=f″(0)f″(0)(1−ϕ)2.5 (52)
Heat transfer parameter
hx=−knfTw−T∞(∂T∂y)y=0=−knfθ′(0)1x(14Grx)1/4 (53)
The local nusselt number
The local Nusselt number is
Nux=hxxknf=−(xTw−T∞)(∂T∂y)y=0=−θ′(0)(14Grx)1/4Nux=−θ′(0)√2Gr1/4x=f((Pr)Gr1/4x) (54)
where ϕ(Pr)=−θ′(0)√2 is a function of Prandtl number. The dependence of ϕ on the Prandtl number is evidenced by Eq. (54).
It could also be shown that
Nux(Rex)1/2=−knfkfθ′(0)=−[ks+(m−1)kf−(m−1)ϕ(kf−ks)ks+(m−1)kf+ϕ(kf−ks)]θ′(0) (55)
where Rex and Grx are the local Reynold and Grashof numbers defined as:
Rex=uxνnf and Grx=gβ(Tw−T∞)x3ν3
Tables 5–7 present various comparisons of results of the present study and the past works for viscous fluid i.e. when the volume fraction of the nanoparticle is zero (ϕ=0). Also, setting half of the cone angle to infinity, i.e. and neglecting the magnetic effects. It could be seen from the Tables that there are excellent agreements between the past results and the present study. Moreover, the Tables present the effects of Prandtl number on the flow and heat transfer processes.
| f''(0) | |||
|
Pr |
Sparrow &Gregg5 |
Kuiken8 |
Present Study |
|
0.003 |
1.0223 |
1.0151 |
1. 0224 |
|
0.008 |
0.9955 |
0.9801 |
0.9955 |
|
0.02 |
0.959 |
0.9284 |
0.9591 |
|
0.03 |
0.9384 |
0.8966 |
0.9384 |
Table 5 Comparison of results for the skin friction parameter
| f(∞) | |||
|
Pr |
Sparrow &Gregg5 |
Kuiken8 |
Present Study |
|
0.003 |
8.7060 |
8.8763 |
8.7061 |
|
0.008 |
5.4018 |
5.4152 |
5.4018 |
|
0.020 |
3.4093 |
3.4055 |
3.4093 |
|
0.030 |
2.7878 |
2.7710 |
2.7878 |
Table 6 Comparison of results of f(∞)
| Nux/(GxPr2)14=−θ′(0) | |||
|
Pr |
Sparrow &Gregg5 |
Kuiken8 |
Present Study |
|
0.003 |
0.5827 |
0.5827 |
0. 5827 |
|
0.008 |
0.5729 |
0.5714 |
0.5728 |
|
0.020 |
0.5582 |
0.5546 |
0.5582 |
|
0.030 |
0.5497 |
0.5443 |
0.5497 |
Table 7 Comparison of results of -Θ1(0)
Effect of cone angle on nanofluid velocity and temperature distributions
The variations of the flow velocity and the temperature gradient of the fluid are inversely proportional to half of the cone angle, γ increases. It should be noted that as the angle increases, the applied magnetic field decreases. Also, the skin friction factor in terms of shear stress and heat transfer rate in terms of Nusselt number are decreased.
Figure 5 shows the effects of magnetic parameter on the fluid velocity and the temperature. As in the preceding parametric study, the fluid velocity and the temperature decrease as the magnetic field increases. This is because, magnetic field creates a flow resistance force called Lorentz force in the flow. The presence of this force in the flow slows fluid motion at boundary layer on solid walls. Consequently, there is decrease the fluid velocity and increase fluid temperature within the boundary layer. And by extension, the skin friction factor in terms of shear stress and heat transfer rate in terms of Nusselt number are decreased.
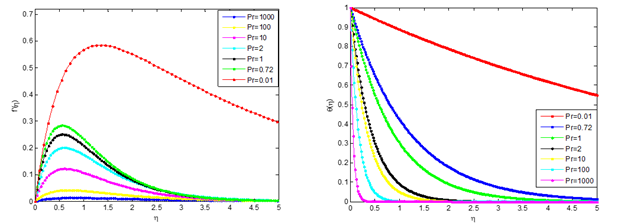
Figure 5 (a) Effects of Prandtl number on the velocity profile when ϕ=0.020, (b) Effects of Prandtl number on temperature profile when ϕ=0.020.
Effect of flow medium porosity on nanofluid velocity and temperature distributions Effects of Darcy number which represent flow medium porosity parameter on the flow velocity and temperature distributions are presented in Figure 6. It is depicted in the figure that as the porosity parameter increases the flow velocity of the fluid decrease while the temperature distribution in the flow increases as the Darcy number increases.
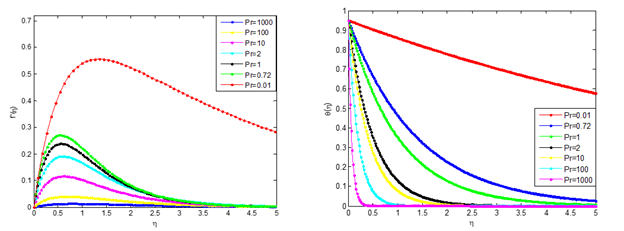
Figure 6 (a) Effects of Prandtl number on the velocity profile when ϕ=0.040, (b) Effects of Prandtl number on temperature profile when ϕ=0.040.
Effect of nanoparticle volume fraction on the velocity and temperature distributions
It has been shown in some previous studies that the presence of nanoparticles in a fluid has significant effects on the flow behaviours of fluid. Figures 7&8 show the effects nanoparticle concentration/volume fraction and Prandtl number on velocity and temperature profiles of copper (II) oxide-water nanofluid. It is indicated in the Figures that as the volume-fraction or concentration of the nanoparticle in the nanofluid increases, the velocity decreases. However, an opposite trend in the temperature profile is observed i.e. the nanofluid temperature increases as the volume-fraction of the nanoparticles in the basefluid increases.This is because, the solid volume fraction has significant impacts on the thermal conductivity. The increased volume fraction of nanoparticles in basefluid results in higher thermal conductivity of the basefluid which increases the heat enhancement capacity of the basefluid. Also, one of the possible reasons for the enhancement on heat transfer of nanofluids can be explained by the high concentration of nanoparticles in the thermal boundary layer at the wall side through the migration of nanoparticles. It should also be stated that the thickness of thermal boundary layer rises with increasing the values of nanoparticle volume fraction. This consequently reduces the velocity of the nanofluid as the shear stress and skin friction are increased.
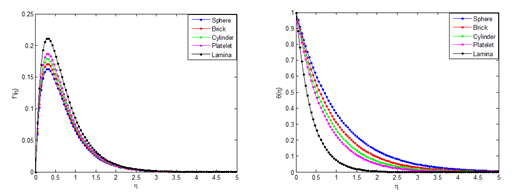
Figure 7 (a) Effect of nanoparticle shape on velocity distribution of the nanofluid, (b) Effects of nanoparticle shape on temperature distribution of nanofluid.
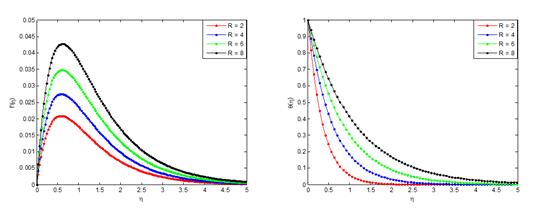
Figure 8 (a) Effects of radiation parameter on the velocity profile of the nanofluid, (b) Effects of radiation parameter on temperature profile of the nanofluid.
Furthermore, the figures show the effects of Prandtl number (Pr) on the velocity and temperature profiles. It is indicated that the velocity of the nanofluid decreases as the Pr increases but the temperature of the nanofluid increases as the Pr increases. This is because the nanofluid with higher Prandtl number has a relatively low thermal conductivity, which reduces conduction, and thereby reduces the thermal boundary-layer thickness, and as a consequence, increases the heat transfer rate at the surface. For the case of the fluid velocity that decreases with the increase of Pr, the reason is that fluid of the higher Prandtl number means more viscous fluid, which increases the boundary-layer thickness and thus, reduces the shear stress and consequently, retards the flow of the nanofluid. Also, it can be seen that the velocity distribution for small value of Prandtl number consist of two distinct regions. A thin region near the wall of the plate where there are large velocity gradients due to viscous effects and a region where the velocity gradients are small compared with those near the wall. In the later region, the viscous effects are negligible and the flow of fluid in the region can be considered to be inviscid. Also, such region tends to create uniform accelerated flow at the surface of the plate.
It is shown in this study that the use of nanoparticles in the fluid exhibited better properties relating to the heat transfer of fluid than heat transfer enhancement through the use of suspended millimeter- or micrometer-sized particles which potentially cause some severe problems, such as abrasion, clogging, high pressure drop, and sedimentation of particles. The very low concentrations applications and nanometer sizes properties of nanoparticles in basefluid prevent the sedimentation in the flow that may clog the channel. It should be added that the theoretical prediction of enhanced thermal conductivity of the basefluid and prevention of clogging, abrasion, high pressure drop and sedimentation through the addition of nanoparticles in basefluid have been supported with experimental evidences in literature.
Effect of nanoparticle shape on the velocity and temperature distributions
The impact of nanoparticle shape at different values of Prandtl number on velocity and temperature profiles of Copper (II) Oxide-water nanofluid is shown in Figure 9. It is indicated that the maximum decrease in velocity and maximum increase in temperature are caused by lamina, platelets, cylinder, bricks and sphere, respectively. It is observed that lamina shaped nanoparticle carries maximum velocity whereas spherical shaped nanoparticle has better enhancement on heat transfer than other nanoparticle shapes. This is because the lamina nanoparticle has greater shape factor than other nanoparticles of different shapes. The enhancement observed at lower volume fractions for non-spherical particles is attributed to the percolation chain formation, which perturbs the boundary layer and thereby increases the local Nusselt number values.
It is evident from this study that proper choice of nanoparticles will be helpful in controlling velocity and heat transfer. It is also observed that irreversibility process can be reduced by using nanoparticles, especially the spherical particles. This can potentially result in higher enhancement in the thermal conductivity of a nanofluid containing elongated particles compared to the one containing spherical nanoparticle, as exhibited by the experimental data in the literature.
Effect of thermal radiation parameter on the velocity and temperature distributions
The variation in the thermal radiation parameter is directly proportional to the velocity of the fluid to increase. This is because as the radiation parameter is augmented, the absorption of radiated heat from the heated plate releases more heat energy released to the fluid and the resulting temperature increases the buoyancy forces in the boundary layer which also increases the fluid motion and the momentum boundary layer thickness accelerates. This is expected, because the considered radiation effect within the boundary layer increases the motion of the fluid which increases the surface frictions.
The influence of radiation parameter on the temperature field is illustrated in Figure 11. Increase in the radiation parameter contributes in general to increase in the temperature of the nanofluid. This is because, as the thermal radiation increases, the absorption of radiated heat from the heated plate releases heat energy released to the fluid the thermal boundary layer of fluid increases as the temperature near the boundary is enhanced.
The analysis of magnetohydrodynamics natural convection of nanofluid flow over a vertical circular cone immersed in a porous medium under the influence of thermal radiation have been carried out in this work using multi-step differential transformation method. Effects of various parameters of the flow and heat transfer models on the fluid-dynamic and thermal behaviours of the nanofluid have been examined and discussed using the approximate analytical solutions. Also, the accuracies of the developed analytical solutions were evaluated by comparing the results of the present study with the results of the numerical solutions and the past studies. It is believed that this study will create a better physical insight into the flow process for the design of flow and heat transfer equipment.
None.
There are no conflicts of interest.
None.

©2020 Sobamowo, et al. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.