International Journal of
eISSN: 2475-5559


Research Article Volume 1 Issue 4
1Faculty of Exact Sciences and Technology, National University of Tucuman, Argentina
1Faculty of Exact Sciences and Technology, National University of Tucuman, Argentina
Correspondence: Monica Beatriz Gramajo, Department of Physics, Faculty of Exact Sciences and Technology, National University of Tucuman, Argentina
Received: November 16, 2016 | Published: December 28, 2016
Citation: Gramajo MB, Veliz JH, Cases AM. LLE of Methanol-Methylcyclohexane-Isooctane-Benzene Quaternary System. Int J Petrochem Sci Eng 2016;1(4):100-104. DOI: 10.15406/ipcse.2016.01.00021
Aquaternary system {methanol + methylcyclohexane + isooctane + benzene} was studied at T = 303.15 K. Only after all ternary equilibria data were determined experimentally, the quaternary binodal surface could be characterized fully. For this purpose, tie line data of {methanol + methylcyclohexane + benzene} ternary systems were obtained at the same temperature, while data for {methanol + isooctane+ benzene}, and {methanol + + isooctane + methylcyclohexane} were taken from literature. Experimental results show that the binodal surface with four quaternary sectional planes P1, P2, P3, P4 with several methylcyclohexane/isooctane in the solid diagram is small and that the highest benzene mass fraction values beyond which only one phase is present for the methanol-rich phase and hydrocarbon-rich one, respectively, are: 0.046 and 0.053 for P1, 0.053 and 0.057 for P2, 0.055 and 0.049 for P3, 0.034 and 0.041 for P4. So, if this quaternary system contains the correct methanol and hydrocarbons concentrations, this blend can be used as a reformulated gasoline because no phase separation should be observed. The distribution of benzene between both phases was also analysed. Ternary experimental results were correlated with the UNIQUAC and NRTL equation.. The UNIQUAC equation is more accurate than the NRTL equation for the ternary systems studied here. The equilibria data of the three ternary systems were used to determine interactions parameters for the UNIQUAC equation. The UNIQUAC equation fitted to the experimental data is more accurate than the UNIFAC method for this quaternary system. The main reason for this is that F is fit in the size of the quaternary binodal surface.
Keywords: Data; Liquid-liquid equilibria; Ternary system; Quaternary system
In recent years, there has been an increasing demand to use oxygenated compounds in the reformulation of gasoline in order to substantially reduce toxic emissions into the environment and simultaneously enhance the octane number of gasoline. This is the reason why we studied the phase equilibria of systems containing representative hydrocarbons of gasoline (benzene, isooctane, or cyclohexane) and oxygenated compounds (methanol, ethanol, or methyl tert-butyl ether).1-8
The US Environmental Protection Agency recommends the use of alcohols as gasoline additives to provide antiknock properties and to help reduce harmful combustion emissions. However, methanol presents partial miscibility with aliphatic hydrocarbons, but not with aromatic ones. Therefore, it is of great importance to study systems composed of methanol and representative hydrocarbons of gasoline.7,8
Keeping this in mind, a quaternary system containing methanol, methylcyclohexane, benzene and isooctane {w1 CH4O + w2 C7H14 + w3 C8H18+ w4 C6H6} was also studied at 303.15K. Tie line data for the methanol-methylcyclohexane-benzene {w1 CH4O + w2 C7H14 + w3 C6H6} ternary system, where w is the mass fraction, were also investigated at temperature the same temperature, while data for methanol- isooctane-benzene, and methanol-isooctane- methylcyclohexane were taken from literature.8 The fourth ternary subsystem methylcyclohexane-isooctane-benzene is completely miscible. This particular temperature was selected because it is representative of tropical and subtropical climates. Table 1 shows the respective Treybal9 classification types for these systems.
| nº | Type | System |
|---|---|---|
1 |
1 |
w1 CH4O + w2 C7H14 + (1- w1-w2) C6H6 |
Table 1: Ternary and quaternary systems, including their Treybal’s classification type; denotes mass fraction of component i.
The experimental data for the ternary systems studied here were correlated with the UNIQUAC (Universal Quasi-Chemical equation)10 and NRTL (Non-Random, Two-Liquid)11 models.
All the pairs of the UNIQUAC interaction parameters obtained from the three partially miscible ternary subsystems included in the quaternary system were averaged and they were then used to predict the quaternary LLE of this model. The original UNIFAC (UNIQUAC Functional-group Activity Coefficients) method was also used for this purpose.12 To the best of our knowledge, there is no reference in the literature on the LLE of the quaternary system studied in this work.
Materials
Methanol was supplied by Merck, while methylcyclohexane and benzene by Sigma-Aldrich and isooctane by Sintorgan (Argentina). The purity of the chemicals was verified chromatographically, which showed that their mass fractions were higher than 0.998. Therefore, they were used without further purification. Methanol was maintained over 0.3 nm activated molecular sieves to prevent water absorption.
Methods
The experimental procedure used in the present study is the same as that reported in a previous work.2 Quantification of all components in the conjugate phases was made by gas chromatography using the internal standard method. Acetone (C3H6O) (Merck, chromatographic quality) with a mass fraction purity >0.999 (GC) was the standard compound used for this purpose. A Hewlett Packard 6890 gas chromatograph with an automatic injector (Agilent G2613A) directly connected to a Chem Station (HP G2070AA) was used. Adequate separation of the five components was obtained on a 30 m long ´ 0.25 mm id ´ 0.5 mm film thickness capillary column (INN Wax, cross-linked polyethylene glycol, HP 19091N-233). The temperature program used was: initial temperature 343 K for two minutes, ramp 50 K·min-1, and final temperature 473 K for another two minutes. The nitrogen carrier gas flow rate was electronically kept constantly working with a split ratio of 20:1 and with the injector maintained at 453 K. Detection was carried out by a thermal conductivity detector at 523 K. Three or four analyses were performed for each sample in order to obtain a mean mass fraction value with repeatability better than one percent.
In order to obtain a calibration curve for each component of the internal standard method, a Mettler AG245 dual range balance with an accuracy of ± 0.1/0.01 mg was used to weigh the chemicals with the highest accuracy. Furthermore, to obtain overall mixtures for LLE studies, we weighed the components with the lowest balance accuracy. For the four components, linear correlations always provided the best fit for chromatography calibration curves.
To validate the reported mass fraction values, three samples of different known overall compositions (determined by mass) were analyzed. These mixtures were analysed with the chromatographic method and their chromatographic concentrations were compared with those obtained by mass. This comparison shows that the reported mass fraction values have an uncertainty of ± 0.001.
In order to determine the quaternary binodal surface, measurements were carried out at four different methylcyclohexane/isooctane ratios, which characterize four quaternary planes (named P1, P2, P3, and P4 in (Figure 1). Figure 1 shows a schematic representation of {w1 CH4O + w2 C7H14 + w3 C8H18 + w4 C6H6} quaternary system. The equilibria data for this system were obtained with the same procedure used in the ternary systems. In this work, the initial mixtures (corresponding to the P1, P2, P3, and P4 planes) were selected to determine tie lines within the whole heterogeneous region
Table 2 lists the (liquid + liquid) equilibria data for the ternary systems {w1 CH4O + w2 C7H14 + w3 C6H6} at temperature (303.15 ± 0.05) K. Figure 2 shows the corresponding LLE diagrams. Data correlated by the UNIQUAC and NRTL models are also shown.
Global compositions |
wi wi |
|||||||
w1 |
w2 |
w3 |
w1 |
w2 |
w3 |
w1 |
w2 |
w3 |
CH4O |
C7H14 |
C6H6 |
CH4O |
C7H14 |
C6H6 |
CH4O |
C7H14 |
C6H6 |
0.3537 |
0.6462 |
0 |
0.677 |
0.323 |
0 |
0.067 |
0.933 |
0 |
0.3479 |
0.6485 |
0.0236 |
0.651 |
0.328 |
0.021 |
0.072 |
0.902 |
0.026 |
0.3379 |
0.6199 |
0.0422 |
0.607 |
0.354 |
0.039 |
0.079 |
0.875 |
0.046 |
0.3245 |
0.6111 |
0.0643 |
0.56 |
0.38 |
0.06 |
0.133 |
0.799 |
0.069 |
0.3076 |
0.6098 |
0.0826 |
0.51 |
0.415 |
0.075 |
0.191 |
0.722 |
0.087 |
PPa |
0.34 |
0.567 |
0.092 |
0.34 |
0.567 |
0.092 |
||
PPb |
0.338 |
0.571 |
0.091 |
0.338 |
0.571 |
0.091 |
||
Table 2 (Liquid+liquid) equilibrium data of {w1 CH4O + w2 C7H14 + w3 C6H6} ternary system at temperature (303.15 ± 0.05) K; wi denotes mass fraction of component i.
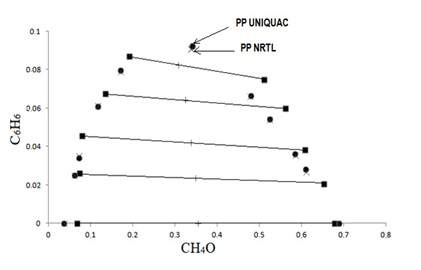
Table 3 lists (liquid + liquid) equilibria data, expressed in mass fraction, of {w1 CH4O + w2 C7H14 + w3 C8H18+ w4 C6H6} quaternary system for each quaternary plane: P1 = (0.8067 C7H14 + 0.1933 C8H18), P2 = (0.6026 C7H14 + 0.3974 C8H18), P3 = (0.3996 C7H14 + 0.6004 C8H18), and P4 = (0.1926 C7H14 + 0.8074 C8H18). Experimental results reported in Table 2 & 3 satisfy the mass balance with a maximum deviation of 5 mass percent.
Global compositions |
wi |
wi |
|---|---|---|
w1 w2 w3 w4 |
w1 w2 w3 w4 |
w1 w2 w3 w4 |
CH4O C7H14 C8H18 C6H6 |
CH4O C7H14 C8H18 C6H6 |
CH4O C7H14 C8H18 C6H6 |
P1 = (0.8067 C7H14 + 0.1933 C8H18) |
|
|
0.3803 0.4999 0.1198 0 |
0.636 0.296 0.068 0 |
0.056 0.760 0.184 0 |
0.3957 0.4775 0.1144 0.0124 |
0.615 0.303 0.070 0.012 |
0.085 0.723 0.179 0.013 |
0.3626 0.4833 0.1167 0.0374 |
0.514 0.364 0.086 0.036 |
0.133 0.663 0.165 0.039 |
0.3678 0.4707 0.1136 0.0479 |
0.452 0.406 0.096 0.046 |
0.155 0.635 0.157 0.053 |
P2 = (0.6026 C7H14 + 0.3974 C8H18) |
||
0.3848 0.3707 0.2445 0 |
0.602 0.248 0.150 0 |
0.090 0.535 0.375 0 |
0.3811 0.3653 0.2412 0.0124 |
0.578 0.254 0.156 0.012 |
0.092 0.531 0.364 0.013 |
0.3715 0.3553 0.2343 0.0389 |
0.510 0.273 0.180 0.037 |
0.135 0.497 0.326 0.042 |
0.3649 0.3542 0.2338 0.0471 |
0.484 0.283 0.187 0.046 |
0.152 0.482 0.318 0.048 |
0.3754 0.3445 0.2263 0.0538 |
0.435 0.304 0.203 0.053 |
0.192 0.452 0.298 0.057 |
0.3706 0.2515 0.3779 0 |
||
0.3730 0.2408 0.3619 0.0243 |
0.616 0.153 0.231 0 |
0.078 0.368 0.554 0 |
0.3763 0.2359 0.3545 0.0333 |
0.539 0.174 0.262 0.025 |
0.105 0.348 0.524 0.023 |
0.3593 0.2377 0.3571 0.0459 |
0.527 0.175 0.263 0.035 |
0.108 0.344 0.517 0.031 |
0.3741 0.2288 0.3437 0.0534 |
0.482 0.189 0.283 0.046 |
0.126 0.331 0.497 0.046 |
0.448 0.199 0.298 0.055 |
0.153 0.319 0.479 0.049 |
|
P4 = (0.2009 C7H14 + 0.7991 C8H18) |
||
0.3673 0.1219 0.5108 0 |
0.600 0.077 0.323 0 |
0.098 0.174 0.728 0 |
0.3845 0.1168 0.4897 0.0090 |
0.583 0.079 0.329 0.009 |
0.100 0.172 0.720 0.008 |
0.3852 0.1136 0.4763 0.0249 |
0.563 0.079 0.331 0.027 |
0.125 0.164 0.689 0.022 |
0.3688 0.1145 0.4800 0.0367 |
0.520 0.086 0.360 0.034 |
0.150 0.156 0.653 0.041 |
Table 3 Liquid + liquid equilibrium data of {w1 CH4O + w2 C7H14 + w3 C8H18+ w4 C6H6} quaternary system at temperature (303.15 ± 0.05) K; wi denotes mass fraction of component i
Since the concentrations of the four components were individually determined, the sums of the mass fractions for each phase shown in Table 3 may slightly differ from unity. The same consideration is applied to Table 2 for the ternary system (range ± 0.001, in mass fraction).
As can be seen in Table 3, we conclude that the benzene mass fractions values beyond which only one phase is present for the methanol-rich phase and hydrocarbon-rich are 0.046 and 0.053 for P1, 0.053 and 0.057 for P2, 0.055 and 0.049 for P3, 0.034 and 0.041 for P4. Since the binodal surface in the solid diagram is small, an adequate blend of these four components could be used as a reformulated gasoline, because no phase separation would occur.
The LLE data for the ternary systems studied here were correlated by the UNIQUAC and NRTL activity coefficient models, using an iterative computer program developed by Sørensen13 that minimizes the values of the following objective functions:
Fa=∑k∑i{(aIik−aIIik)/(aIik−aIIik)}2 (1)
Fa=∑kmin∑i∑j(Xijk−Xijk)2+Q∑nP2n (2)
Here, aI,IIik are the activities obtained from the experimental concentrations, I and II are the phases, xijk and are the experimental mole fraction values of the liquid phase and the calculated tie line lying close to the considered experimental line, respectively, where i represents the components, j the phases, and k the tie lines. Pn and Q are the parameter and the constant values in the penalty term, respectively.
This penalty term was established to reduce the risk of multiple solutions associated with high parameter values. Table 4 shows the structural parameters of the pure components taken from the literature14 and the optimised binary interaction parameters of the UNIQUAC and NRTL models, for the ternary systems. The non-randomness parameter for the NRTL equation is also given.
Goodness of fit, as measured by the r.m.s. deviation in mole fraction F, is given by
F=100 {∑k∑i∑j(xijk−ˆxijk)2/2nM}12, (3)
Where n is the number of components in the system. The r.m.s. relative error in the solute distribution ratio Δm is given by
Unexpected text node: ' ' , (4)
Table 4 shows the UNIQUAC structural parameters for the pure components taken from the literature [14]. The calculated values of the residuals F and Δm, the optimized non-randomness parameter for the NRTL equation aij, and the optimized binary interaction parameters for UNIQUAC and NRTL models are also listed in Table 4. Here xijk , is the experimental mole fraction of the ith component in the jth phase on the kth tie line, Unexpected text node: ' ' is the corresponding calculated value, and mk and Unexpected text node: ' ' are the experimental and calculated solute distribution ratios, respectively, given by w"2/w'2 .
Figure 2 shows the NRTL and UNIQUAC equations. The UNIQUAC equation fitted to the experimental results is considerably more accurate than NRTL equation taking into account overall errors, F and and Δm, listed in Table 4.
F% |
%mD |
i,j |
aij b |
aji b |
jia |
UNIQUAC |
|||||
0.4 |
17.9 |
1.2 |
-1.5929 |
706.08 |
|
1.3 |
345.14 |
-98.318 |
|||
2.3 |
606.45 |
-274.16 |
|||
NRTL |
|||||
0.3 |
50.7 |
1.2 |
499.24 |
564.43 |
0.3 |
1.3 |
995.17 |
-515 |
|||
2.3 |
1021.7 |
-562.3 |
Table 4 Residuals F and Dm for UNIQUAC and NRTL optimised parameters of the UNIQUAC and NRTL equations, and non-randomness parameter (aij), for the system {w1 CH4O + w2 C7H14 + (1- w1-w2) C6H6} at temperature 303.15 Ka.
Table 5 lists the residuals for the UNIFAC and UNIQUAC models of {w1 CH4O + w2 C7H14 + w3 C8H18+ w4 C6H6} quaternary system. The fit was poor in terms of m for both models, due to the large relative error associated with the very low concentrations of benzene in both phases, while the goodness of fit in terms of Fwas satisfactory, particularly for the UNIQUAC model. Therefore, the UNIQUAC equation fitted to the experimental data is more accurate than the UNIFAC method of this quaternary system.
Planes |
F% |
Dm% |
UNIFAC |
||
P1 |
17.2 |
39.5 |
P2 |
16.4 |
34.6 |
P3 |
14.6 |
40.6 |
P4 |
11.7 |
33.6 |
UNIQUAC |
||
P1 |
3.4 |
46.7 |
P2 |
4.6 |
74 |
P3 |
3 |
81.1 |
P4 |
1.5 |
66.5 |
Table 5 Residuals F and Δ
m of {w1 CH4O + w2 C7H14 + w3 C8H18+ w4 C6H6} quaternary system at temperature 303.15 Ka.
a: The values of Δm were calculated only for C6H6. The distribution coefficient for this compound is defined as m = mass fraction of C6H6 in the II phase (w"4 )/mass fraction of C8H10 in the I phase ( w"4).
i-j |
aij |
aji |
1-2 |
-4.6795 |
664.945 |
1-3 |
-19.3145 |
647.465 |
1-4 |
183.0015 |
22.481 |
2-3 |
-17.974 |
27.111 |
2-4 |
606.45 |
-274.16 |
3-4 |
-5.2652 |
-5.5424 |
Table 6 Average UNIQUAC interaction parameters for the prediction of the quaternary system.
(Liquid + liquid) equilibria of {w1 CH4O + w2 C7H14 + w3 C6H6} ternary systems and of {w1 CH4O + w2 C8H18 + w3 C7H14 + w4 C8H10} quaternary system were investigated at temperature 303.15 K, and the highest concentrations of hydrocarbons and methanol beyond which only one phase is present were established.
The UNIQUAC equations fitted to the experimental data is considerably more accurate than the NRTL equations taking into account both overall errors F and Δm These residuals also show that the UNIQUAC model is better than the NRTL one Table 4 for the ternary systems.
The quaternary equilibria was predicted by the UNIQUAC and UNIFAC models, showing that the fit was poor in terms of Δm for both models, due to the large relative error associated with the very low concentrations of benzene in both phases, while the goodness of fit in terms of F was satisfactory, particularly for the UNIQUAC model. Therefore, The UNIQUAC equation fitted to the experimental data is more accurate than the UNIFAC method of this quaternary system. The main reason for this is that F is fit in the size of the quaternary binodal surface.
a : Activity obtained directly from the model by insertion of the experimental
concentrations; eq. (1)
aij, aji : Parameters of the UNIQUAC and NRTL models
F : r.m.s. deviation in mole fraction given by eq. (3)
Fa, Fx : Objective function given by equations (1) and (2).
LLE : Liquid-liquid equilibria
mk : Experimental solute distribution ratio; eq. (4)
Unexpected text node: ' ' : Calculated solute distribution ratio; eq. (4)
Dm : r.m.s. relative error in the solute distribution ratio given by eq. (4)
M : Number of tie lines; equations (3) and (4)
n : Number of the components in the system (3) or (4)
Pi : Quaternary planes for the construction of the binodal surface
Pn : Parameter in the penalty term; equations (1) and (2)
PP : Plait point
Q : Constant value in the penalty term; equations (1) and (2)
r.m.s. : Root mean square deviation
wi : Mass fraction of component i
xijk
: Experimental mole fraction of the ith component in the jth phase on the kth tie line
(Equations (2) and (3))
Unexpected text node: ' x
: Calculated mole fraction of the ith component in the jth phase on the kth tie-line
(Equations (2) and (3))
Unexpected text node: ' ' : Mass fraction of the ithcomponent in the methanol (’) phase
w"i : Mass fraction of the ith component in the hydrocarbon (’’) phase
i : lower index-denoting components (1-4)
j : lower index-denoting phases (’ or ’’)
k : lower index denoting tie lines (1 to M)
’ : methanol phase
’’ : hydrocarbon phase
Financial support from the Consejo de Investigaciones de la Universidad Nacional de Tucumán, Argentina (CIUNT, Grant 26/E518) and Secretaria de Políticas Universitarias de la Nación Argentina “Proyecto Jorge Sabato” Res. Nº 1150 SPU, 20/02/2016 are gratefully acknowledged.
The author declares no conflict of interest.

©2016 Gramajo, et al. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.