The expanding applications of viscoelastic fluids in biomedical engineering and industrial processes require proper under and physical insights into the flow phenomena of the fluids. In this work, simultaneous effects of slip and magnetic field on the flow of an upper convected Maxwell (UCM) nano fluid through a permeable micro channel embedded in porous medium are analyzed using homotopy analysis method. The results of the approximate analytical solution depict very good agreements with the results of the fifth-order Runge-Kutta Fehlberg method (Cash-Karp Runge-Kutta) coupled with shooting methodfor the verification of the mathematical method used in analyzing the flow. Thereafter, the obtained analytical solutions are used to investigate the effects of pertinent rheological parameters on flow. It is observed from the results that increase in slip parameter, nano particle concentration and Darcy number lead to increase in the velocity of the upper-convected Maxwell fluid while increase in Deborah’s, Hartmann, and Reynold numbers decrease the fluid flow velocity towards the lower plate but as the upper plate is approached a reverse trend is observed. The study can be used to advance the application of upper convected Maxwell flow in the areas of in biomedical, geophysical and astrophysics.

Keywords: slip analysis, upper-convected maxwell flow, viscoelastic nano fluid, magnetic field, porous medium

The vast areas of applications and the importance of the viscoelastic fluid flow in modern science and engineering such as gaseous diffusion, blood flow through oxygenators, flow in blood capillaries have continue to aroused the research interests. Complex rheological fluids such as blood, paints, synovial fluid, saliva, jam which cannot be adequately described by Navier Stokes. This lead to the development of complex constitutive relations to capture the flow behaviour of the complex fluids.¹ Among the newly developed fluid models of the integral and differential-type models, Upper convected Maxwell fluid model has showed to be an effective fluid model that capture these phenomena of fluids especially of those with high elastic behaviours such as polymer melts. Since highly elastic fluids have high Deborah number.^2,3 In the analysis of Maxwell flow, Fetecau ⁴ presented a new exact solution for flow though infinite micro channel while Hunt⁵ studied convective fluid flow through rectangular duct. Sheikholeslami et al.⁶ investigated magneto hydrodynamic field effect on flow through semi-porous channel utilizing analytical methods. Shortly after, Sheikholeslami ^7-9 adopted numerical solutions in the investigations of nanofluid in semi-annulus enclosure. Flow of upper convected Maxwell fluid through porous stretch sheet was investigated by Raftari and Yildirim.¹⁰ Entophy generation in fluid in the presence of magnetic field was analyzed by Sheikholeslami and Ganji ¹¹ using lattice Boltzman method while Ganji et al.¹² used analytical and numerical methods for the fluid flow problems under the influence of magnetic field. The flow of Viscoelastic fluid through a moving plate was analyzed by Sadeghy and Sharifi ¹³ using local similarity solutions. Mass transfer and flow of chemically reactive upper convected Maxwell fluid under induced magnetic field was investigated by Vajrevulu et al.¹⁴ Not long after Raftari and Vajrevulu ¹⁵ adopted the homotopy analysis method in the study of flow and heat transfer in stretching wall channels considering MHD. Hatamiet al. ¹⁶ presented forced convective MHD nano fluid flow conveyed through horizontal parallel plates. Laminar thermal boundary flow layer over flat plate considering convective fluid surface was analyzed by Aziz ¹⁷ using similarity solution. Beg and Makinde ¹⁸ examined the flow of viscoelastic fluid through Darcian microchannel with high permeability.

Most of the above reviews studies focused on the analysis of fluid flow under no slip condition. However, such an assumption of no slip condition does not hold in a flow system with small size characteristics size or low flow pressure. The pioneer work of flow with slip boundary condition was first initiated by Navier.¹⁹ Such an important condition (slip conditions) occur in various flows such as nano fluids, polymeric liquids, fluids containing concentrated suspensions, flow on multiple interfaces, thin film problems and rarefied fluid problems.^19–31 Due to the practical implications of the condition of flow processes, several studies on the effects of slip boundary conditions on fluids flow behaviours have been presented by many researchers.^19–32Abbasi et al.³³ investigated the MHD flow characteristics of upper-convicted Maxwell viscoelastic flow in a permeable channel under slip conditions. However, an analytical study on simultaneous effects of slip, magnetic field, nano particle and porous medium on the flow characteristics of an upper-convected Maxwell viscoelastic nano fluid has not been carried out in literature. Therefore, in this work, slip flow analysis of an upper-convected Maxwell viscoelastic nano fluid through a permeable micro channel embedded in porous medium under the influence of magnetic field is analyzed. The nonlinear partial differential equations governing the flow phenomena are converted to a nonlinear ordinary differential equation using similarity transformation. Thereafter, the ordinary differential is solved using homotopy analysis method. 

Model Development and Analytical Solution

Consider a laminar slip flow of an electrically conducting fluid in a microchannel is considered. Along the y axis, magnetic field are imposed uniformly, as described in the physical model diagram (Figure 1) It is assumed external electric field is zero and constant of electrical conductivity is constant. Therefore, magnetic Reynolds number is smalland magnetic field induced by fluid motion is negligible.

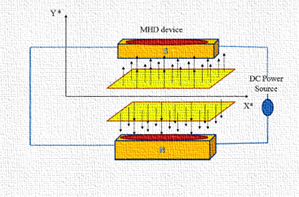
Figure 1 Flow of upper-convected Maxwell fluid between in permeable channel embedded in porous medium.

Based on the assumptions, the governing equation for the Maxwell fluid is presented as [8]

$T-pI+S$   (1)

Where the Cauchy stress tensor is T and S is the extra-stress Tensor which satisfies

$S+\lambda \left(\frac{ds}{dt}-LS-S{L}^T\right)\mu A_L$   (2)

The Rivlin-Ericksen tensor is defined by

$A_L=\nabla V+{\left(\nabla V\right)}^T$   (3)

The continuity and momentum equation’s for steady, incompressible two dimensional flows are expressed as

$\frac{\partial \overline{u}}{\partial x}+\frac{\partial \overline{v}}{\partial y}=0$   (4)

${\rho }_{nf}\left(u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)=-\frac{\partial P}{\partial x}+\frac{\partial S_{xx}}{\partial x}+\frac{\partial S_{xy}}{\partial y}-{\sigma }_{nf}{B}^2(t)u-\frac{{\mu }_{nf}u}{K_p},$   (5)

${\rho }_{nf}\left(\overline{u}\frac{\partial \overline{v}}{\partial x}+\overline{v}\frac{\partial \overline{v}}{\partial y}\right)=-\frac{\partial P}{\partial x}+\frac{\partial S_{yx}}{\partial x}+\frac{\partial S_{yy}}{\partial y}-\frac{{\mu }_{nf}\overline{v}}{K_p},$   (6)

where the effective density $\rho nf$  and effective dynamic viscosity ${\mu }_{nf}$  of the nanofluid are defined as follows:

${\rho }_{nf}=\left(1-\varphi \right){\rho }_f+\varphi {\rho }_s,$   (7)

${\mu }_{nf}=\frac{{\mu }_f}{{\left(1-\varphi \right)}^{2.5}},$   (8)

${\sigma }_{nf}={\sigma }_f\left[1+\frac{3\left\{\frac{{\sigma }_s}{{\sigma }_f}-1\right\}\varphi }{\left\{\frac{{\sigma }_s}{{\sigma }_f}+2\right\}\varphi -\left\{\frac{{\sigma }_s}{{\sigma }_f}-1\right\}\varphi }\right],$   (9)

S_xx,S_xy,S_yx and S_yy are extra stress tensors and ρ is the density of the fluid.

Using the shear-stress strain for a upper-convected liquid, The governing equations of fluid motion is easily expressed as

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$   (10)

$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+\lambda \left(u^2\frac{{\partial }^{2}u}{\partial x^2}+v\frac{{\partial }^{2}u}{\partial y^2}+2uv\frac{{\partial }^{2}u}{\partial x\partial y}\right)=v_{nf}\frac{{\partial }^{2}u}{\partial y^2}-\frac{{\sigma }_{nf}{B}^2(t)u}{{\rho }_{nf}}-\frac{{\nu }_{nf}u}{K_p},$   (11)

where flow velocity component (u,v) are velocity component along the xand y directions respectively. Since flow is symmetric about channel center line, attention is given to the flow region 0<y<H. Appropriate boundary condition is given as [14]:

$y=0:\frac{\partial u}{\partial x}=0,v=0$   (12)

$y=H:\frac{\partial u}{\partial y}=-\beta u,v=V_w$   (13)

where V_wand β are the wall characteristic suction velocity and sliding friction respectively.

The physical and thermal properties of the base fluid and nano particles are given in Table 1 and Table 2, respectively.

The similarity variables are introduced as:

$\eta =\frac{y}{H},u=-V_{w}x{f}^{\text{'}}(y);v=V_{w}f(y);k=\frac{\mu }{H\beta }$   (14)

With the aid of the dimensionless parameters in Eq. (14), the constitutive relation is satisfied. Equation (2-4) can be expressed as:

$f^{\text{'}\text{'}\text{'}}-\left(M^2+\frac{1}{Da}\right)f^{\text{'}}+{\left(1-\varphi \right)}^{2.5}\left(\left(1-\varphi \right)+\varphi \frac{{\rho }_s}{{\rho }_f}\right)R{e}_w\left(f^{\text{'}2}-f{f}^{\text{'}\text{'}}\right)+De{\left(1-\varphi \right)}^{2.5}\left(2f{f}^{\text{'}}{f}^{\text{'}\text{'}}-f^2{f}^{\text{'}\text{'}\text{'}}\right)=0$   (15)

And the boundary conditions as

$\eta =0:f^{\text{'}\text{'}}=0;f=0$   (16)

$\eta =1:f^{\text{'}}=-k{f}^{\text{'}\text{'}}:f=1$

where ${\mathrm{Re}}_w=\frac{V_{w}H}{\upsilon }$  is the Reynolds number, $De=\frac{\lambda V_w^2}{\upsilon }$ is the Deborah’s number, $M^2=\frac{\sigma B_0^{2}H}{\mu }$ is the Hartman parameter, $Da=\frac{K_p}{H}$ is the Darcy’s number. For Re_w>0 corresponds to suction flow while Re_w<0 correspond to injection flow respectively.

Equ. (13) is a third-order differential equation with four boundary conditions. Through a creative differentiation of Eq. (12). Hence introducing fourth order equation as:

$f^{iv}-\left(M^2+\frac{1}{Da}\right)f^{″}+{\left(1-\varphi \right)}^{2.5}\left(\left(1-\varphi \right)+\varphi \frac{{\rho }_s}{{\rho }_f}\right)R{e}_w\left(f^{\prime }{f}^{″}-f{f}^{‴}\right)+De{\left(1-\varphi \right)}^{2.5}\left(2{f^{\prime }}^2{f}^{\text{'}\text{'}}-2f{f^{″}}^2+f^2{f}^{iv}\right)=0$   (17)

The above Eq. (17) study satisfies all the four boundary conditions

Application of the Homotopy Analysis Method to the Flow Problem

The homotopy analysis method (HAM) which is an analytical scheme for providing approximate solutions to the ordinary differential equations, is adopted in generating solutions to the ordinary nonlinear differential equations .Upon constructing the homotopy, the initial guess and auxiliary linear operator can be expressed as

$f_0(\eta )=-\frac{1}{2(3k+1)}{\eta }^3+\frac{3(2k+1)}{2(3k+1)}\eta$   (18)

$L(f)=f^{\text{'}\text{'}\text{'}\text{'}}$   (19)

$L\left(\frac{1}{6}{c}_1{\eta }^3+\frac{1}{2}{c}_2{\eta }^2+c_3\eta +c_4\right)=0$   (20)

Where $C_i\left(i=1,2,3,4\right)$  are constants? Let $P=\in \left[0,1\right]$ connotes the embedding parameter and  is the non-zero auxiliary parameter. Therefore, the homogony is constructed as

Zeroth-order deformation equations

$\left(1-P\right)L\left[F\left(\eta ;p\right)-f_0(\eta )\right]=p\hslash H(\eta )N\left[F(\eta ;p)\right]$   (21)

$F(0;p)=0;F^{\text{'}\text{'}}\left(0;p\right)=0;F\left(1;p\right)=1;k{F}^{\text{'}\text{'}}\left(1;p\right)+F^{\text{'}}\left(1;p\right)=0$   (22)

$N[F(\eta ;p)]=\frac{d^{4}F\left(\eta ;p\right)}{d{\eta }^4}+{\left(1-\varphi \right)}^{2.5}\left(\left(1-\varphi \right)+\varphi \frac{{\rho }_s}{{\rho }_f}\right)R{e}_w\left[\frac{dF(\eta ;p)}{d\eta }\frac{d^{2}F(\eta ;p)}{d{\eta }^2}-F(\eta ;p)\frac{d^3(\eta ;p)}{d{\eta }^3}\right]$
$-M^2\frac{d^{2}F(\eta ;p)}{d{\eta }^2}-\frac{1}{Da}\frac{d^{2}F(\eta ;p)}{d{\eta }^2}+De{\left(1-\varphi \right)}^{2.5}[2{\left(\frac{dF(\eta ;p)}{d\eta }\right)}^2\frac{d^{2}F(\eta ;p)}{d{\eta }^2}-2F(\eta ;p){\left(\frac{d^{2}F(\eta ;p)}{d{\eta }^2}\right)}^2+{(f(y;p))}^2\frac{d^{4}F\left(\eta ;p\right)}{d{\eta }^4}]$   (23)

when $p=0$  and $p=1$ we have

$F(\eta ;0)=f_0(\eta );F(\eta ;1)=f(\eta )$   (24)

As p increases from 0 to 1. F(_y;p) varies from f₀(y) to f(y). By Taylor’s theorem and utilizing Eq. (26),F(y; p) can be expanded in the power series of p as follows:

$F(\eta ;p)=f_0(\eta )+{\displaystyle \sum _{m-1}^{\infty }{f}_m(\eta )p^m,f_m(\eta )}=\frac{1}{m!}{\frac{{\partial }^m(F(\eta ;p))}{\partial p^m}|}_{p=0}$   (25)

where ℏ  is chosen such that the series is convergent at p1; therefore, by Eq. (24) it is easily shown that

$f(\eta )=f_0(\eta )+{\displaystyle \sum _{m-1}^{\infty }{f}_m(\eta )}$   (26)

Math order deformation equations

$L[f_m(\eta )-{\chi }_m{f}_{m-1}(\eta )]=\hslash H(\eta )R_m(\eta )$   (27)

$F_m(0;p)=0;F^{\text{'}\text{'}}(0;p)=0;F_m(1,p)=0;k{F}_m^{\text{'}\text{'}}(1;p)+F_m^{\text{'}}(1,p)=0$    (28)

$\begin{array}{l}{R}_m(\eta )=f_{m-1}^{\text{'}\text{'}\text{'}\text{'}}+{\displaystyle \sum _{k=0}^{m-1}\left[\begin{array}{l}{\left(1-\varphi \right)}^{2.5}\left(\left(1-\varphi \right)+\varphi \frac{{\rho }_s}{{\rho }_f}\right)R{e}_w\left(f_{m-1}^{\text{'}}{f}_k^{\text{'}\text{'}}-f_{m-1-k}{f}_k^{\text{'}\text{'}\text{'}}\right)+De{\left(1-\varphi \right)}^{2.5}{f}_{m-1-k}^{\text{'}}\left({\displaystyle \sum _{l=0}^k\left(2f_{k-l}^{\text{'}}{f}_l^{\text{'}\text{'}}\right)}\right)\\ -De{\left(1-\varphi \right)}^{2.5}{f}_{m-1-k}\left({\displaystyle \sum _{l=0}^k\left(2f_k^{\text{'}\text{'}}{-}_l{f}^{\text{'}\text{'}}-f_{k-l}{f}_l^{\text{'}\text{'}\text{'}\text{'}}\right)}\right)\end{array}\right]}\\ -M^2{f}_{m-1}^{\text{'}\text{'}}-\frac{1}{Da}{f}_{m-1}^{\text{'}\text{'}}\end{array}$   (29)

Now the results for the convergence, differential equation and the auxiliary function are determined according to the solution expression. So we assume

$H(y)=1$   (30)

The analytic solution is deve,loped using the MATLAB computational stencil. Hence the first deformation is expressed below

$f_1(\eta )=\hslash \left\{\begin{array}{l}-\frac{5}{672}\frac{De{\left(1-\varphi \right)}^{2.5}{\eta }^9}{(3k+1)}-\frac{3}{2}\frac{\left(\begin{array}{l}-0.0071649{\left(1-\varphi \right)}^{2.5}\left(\left(1-\varphi \right)+\varphi \frac{{\rho }_s}{{\rho }_f}\right)R{e}_w-0.042857De-\\ 0.0023810{\left(1-\varphi \right)}^{2.5}\left(\left(1-\varphi \right)+\varphi \frac{{\rho }_s}{{\rho }_f}\right)R{e}_w-0.085714Dek\end{array}\right){\eta }^7}{27k^3+27k^2+9k+1}\\ -\frac{3}{2}\frac{\left(\begin{array}{l}-0.15\left(M^2+\frac{1}{Da}\right)k^2-0.1\left(M^2+\frac{1}{Da}\right)k-0.016667\left(M^2+\frac{1}{Da}\right)+0.3De{k}^2\\ +0.3De{\left(1-\varphi \right)}^{2.5}k+0.075De{\left(1-\varphi \right)}^{2.5}\end{array}\right){\eta }^5}{27k^3+27k^2+9k+1}\\ +\frac{1}{840}\left[\begin{array}{l}\frac{\left(\begin{array}{l}378De{\left(1-\varphi \right)}^{2.5}{k}^3-1890\left(M^2+\frac{1}{Da}\right)k^3-189{\left(1-\varphi \right)}^{2.5}\left(\left(1-\varphi \right)+\varphi \frac{{\rho }_s}{{\rho }_f}\right)R{e}_w{k}^2+2268DDe{\left(1-\varphi \right)}^{2.5}{}^2-\\ 1638\left(M^2+\frac{1}{Da}\right)k^2-90{\left(1-\varphi \right)}^{2.5}\left(\left(1-\varphi \right)+\varphi \frac{{\rho }_s}{{\rho }_f}\right)R{e}_{w}k-462\left(M^2+\frac{1}{Da}\right)k+468De{\left(1-\varphi \right)}^{2.5}k\end{array}\right){\eta }^3}{1+54k^2+12k+108k^3+81k^4}\\ +\frac{\left(-9{\left(1-\varphi \right)}^{2.5}\left(\left(1-\varphi \right)+\varphi \frac{{\rho }_s}{{\rho }_f}\right)R{e}_w+52De{\left(1-\varphi \right)}^{2.5}-42\left(M^2+\frac{1}{Da}\right)\right)}{1+54k^2+12k+108k^3+81k^4}\end{array}\right]\\ -\frac{1}{1120}\left[\begin{array}{l}\frac{\left(\begin{array}{l}-8{\left(1-\varphi \right)}^{2.5}\left(\left(1-\varphi \right)+\varphi \frac{{\rho }_s}{{\rho }_f}\right)R{e}_w-96{\left(1-\varphi \right)}^{2.5}\left(\left(1-\varphi \right)+\varphi \frac{{\rho }_s}{{\rho }_f}\right)R{e}_{w}k-1764\left(M^2+\frac{1}{Da}\right)k^3\\ +1440De{\left(1-\varphi \right)}^{2.5}{k}^2+77De{\left(1-\varphi \right)}^{2.5}k-364\left(M^2+\frac{1}{Da}\right)k\end{array}\right)\eta }{1+54k^2+12k+108k^3+81k^4}+\\ \frac{\left(\begin{array}{l}-1428\left(M^2+\frac{1}{Da}\right)k^2+3528De{\left(1-\varphi \right)}^{2.5}{k}^3-216{\left(1-\varphi \right)}^{2.5}\left(\left(1-\varphi \right)+\varphi \frac{{\rho }_s}{{\rho }_f}\right)R{e}_w{k}^2\\ -28\left(M^2+\frac{1}{Da}\right)+7De{\left(1-\varphi \right)}^{2.5}\end{array}\right)\eta }{1+54k^2+12k+108k^3+81k^4}\end{array}\right]\end{array}\right\}$    (28)

Similarly, f₂(η), f₃(η), f₄(η), f₅(η)… are found but they are too large expressions that cannot be included in this paper. However, they are included in the results displayed graphically.

Convergence of the HAM solution

It is established that the convergence and the rate of approximation for the HAM solution strongly depend on the value of the auxiliary parameter.^34–37The present problem shows a wide of acceptable range of values of for the difference controlling parameters of the model as shown in (Tables 3a-3d.).

Numerical Procedure for the analysis of the governing equation

Eq. (15) is a fourth-order ordinary differential equation which is in this work is analyzed numerically using fifth-order Runge-Kutta Fehlberg method (Cash-Karp Runge-Kutta) coupled with shooting method. Since Runge-Kutta method is for solving first-order ordinary differential equation, the fourth-order ordinary differential equation is decomposed into a system of first-order differential equations as follows:

$f\text{'}=p,$   (29)

$f\text{'}\text{'}=p\text{'}=q,$   (30)

$f\text{'}\text{'}\text{'}=q\text{'}=w,$

$f^{iv}=w\text{'}=z,$   (31)

$z=\left(M^2+\frac{1}{Da}\right)p-{\left(1-\varphi \right)}^{2.5}\left(\left(1-\varphi \right)+\varphi \frac{{\rho }_s}{{\rho }_f}\right)R{e}_w\left(p^2-fq\right)-De{\left(1-\varphi \right)}^{2.5}\left(2fpq-f^{2}w\right)$

The above Eqs. (29)-(31) can be written as

$a\left(\eta ,f,p,q,w,z\right)=p,$   (32)

$b\left(\eta ,f,p,q,w,z\right)=q,$   (33)

$c\left(\eta ,f,p,q,w,z\right)=w,$   (34)

$d\left(\eta ,f,p,q,w,z\right)=z$   (35)

$e\left(\eta ,f,p,q,z\right)=\left(M^2+\frac{1}{Da}\right)p-{\left(1-\varphi \right)}^{2.5}\left(\left(1-\varphi \right)+\varphi \frac{{\rho }_s}{{\rho }_f}\right)R{e}_w\left(p^2-fq\right)-De{\left(1-\varphi \right)}^{2.5}\left(2fpq-f^{2}w\right)$   (36)

The iterative scheme of the fifth-order Runge-Kutta Fehlberg method (Cash-Karp Runge-Kutta) for the above system of first-order equations is given as

$f_{i+1}=f_i+h\left(\frac{2835}{27648}{k}_1+\frac{18575}{48384}{k}_3+\frac{13525}{55296}{k}_4+\frac{277}{14336}{k}_5+\frac{1}{4}{k}_6\right)$   (37)

$p_{i+1}=p_i+h\left(\frac{2835}{27648}{l}_1+\frac{18575}{48384}{l}_3+\frac{13525}{55296}{l}_4+\frac{277}{14336}{l}_5+\frac{1}{4}{l}_6\right)$   (38)

$q_{i+1}=q_i+h\left(\frac{2835}{27648}{m}_1+\frac{18575}{48384}{m}_3+\frac{13525}{55296}{m}_4+\frac{277}{14336}{m}_5+\frac{1}{4}{m}_6\right)$   (39)

$w_{i+1}=w_i+h\left(\frac{2835}{27648}{n}_1+\frac{18575}{48384}{n}_3+\frac{13525}{55296}{n}_4+\frac{277}{14336}{n}_5+\frac{1}{4}{n}_6\right)$   (40)

$z_{i+1}=z_i+h\left(\frac{2835}{27648}{r}_1+\frac{18575}{48384}{r}_3+\frac{13525}{55296}{r}_4+\frac{277}{14336}{r}_5+\frac{1}{4}{r}_6\right)$   (41)

where

$\begin{array}{l}{k}_1=a\left({\eta }_i,f_i,p_i,q_i,w_i,z_i\right)\\ l_1=b\left({\eta }_i,f_i,p_i,q_i,w_i,z_i\right)\\ m_1=c\left({\eta }_i,f_i,p_i,q_i,w_i,z_i\right)\\ n_1=d\left({\eta }_i,f_i,p_i,q_i,w_i,z_i\right)\\ r_1=e\left({\eta }_i,f_i,p_i,q_i,w_i,z_i\right)\end{array}$

$\begin{array}{l}{k}_2=a\left({\eta }_i+\frac{1}{5}h,f_i+\frac{1}{5}{k}_{1}h,p_i+\frac{1}{5}{l}_{1}h,q_i+\frac{1}{5}{m}_{1}h,w_i+\frac{1}{5}{n}_{1}h,z_i+\frac{1}{5}{r}_{1}h\right)\\ l_2=b\left({\eta }_i+\frac{1}{5}h,f_i+\frac{1}{5}{k}_{1}h,p_i+\frac{1}{5}{l}_{1}h,q_i+\frac{1}{5}{m}_{1}h,w_i+\frac{1}{5}{n}_{1}h,z_i+\frac{1}{5}{r}_{1}h\right)\\ m_2=c\left({\eta }_i+\frac{1}{5}h,f_i+\frac{1}{5}{k}_{1}h,p_i+\frac{1}{5}{l}_{1}h,q_i+\frac{1}{5}{m}_{1}h,w_i+\frac{1}{5}{n}_{1}h,z_i+\frac{1}{5}{r}_{1}h\right)\\ n_2=d\left({\eta }_i+\frac{1}{5}h,f_i+\frac{1}{5}{k}_{1}h,p_i+\frac{1}{5}{l}_{1}h,q_i+\frac{1}{5}{m}_{1}h,w_i+\frac{1}{5}{n}_{1}h,z_i+\frac{1}{5}{r}_{1}h\right)\\ r_2=e\left({\eta }_i+\frac{1}{5}h,f_i+\frac{1}{5}{k}_{1}h,p_i+\frac{1}{5}{l}_{1}h,q_i+\frac{1}{5}{m}_{1}h,w_i+\frac{1}{5}{n}_{1}h,z_i+\frac{1}{5}{r}_{1}h\right)\end{array}$

$\begin{array}{l}{k}_3=a\left(\begin{array}{l}{\eta }_i+\frac{3}{10}h,f_i+\frac{3}{40}{k}_{1}h+\frac{9}{40}{k}_{2}h,\text{}\text{}{p}_i+\frac{3}{40}{l}_{1}h+\frac{9}{40}{l}_{2}h,\\ q_i+\frac{3}{40}{m}_{1}h+\frac{9}{40}{m}_{2}h,w_i+\frac{3}{40}{n}_{1}h+\frac{9}{40}{n}_{2}h,z_i+\frac{3}{40}{r}_{1}h+\frac{9}{40}{r}_{2}h\end{array}\right)\\ l_3=b\left(\begin{array}{l}{\eta }_i+\frac{3}{10}h,f_i+\frac{3}{40}{k}_{1}h+\frac{9}{40}{k}_{2}h,\text{}\text{}{p}_i+\frac{3}{40}{l}_{1}h+\frac{9}{40}{l}_{2}h,\\ q_i+\frac{3}{40}{m}_{1}h+\frac{9}{40}{m}_{2}h,w_i+\frac{3}{40}{n}_{1}h+\frac{9}{40}{n}_{2}h,z_i+\frac{3}{40}{r}_{1}h+\frac{9}{40}{r}_{2}h\end{array}\right)\\ m_3=c\left(\begin{array}{l}{\eta }_i+\frac{3}{10}h,f_i+\frac{3}{40}{k}_{1}h+\frac{9}{40}{k}_{2}h,\text{}\text{}{p}_i+\frac{3}{40}{l}_{1}h+\frac{9}{40}{l}_{2}h,\\ q_i+\frac{3}{40}{m}_{1}h+\frac{9}{40}{m}_{2}h,w_i+\frac{3}{40}{n}_{1}h+\frac{9}{40}{n}_{2}h,z_i+\frac{3}{40}{r}_{1}h+\frac{9}{40}{r}_{2}h\end{array}\right)\\ n_3=d\left(\begin{array}{l}{\eta }_i+\frac{3}{10}h,f_i+\frac{3}{40}{k}_{1}h+\frac{9}{40}{k}_{2}h,\text{}\text{}{p}_i+\frac{3}{40}{l}_{1}h+\frac{9}{40}{l}_{2}h,\\ q_i+\frac{3}{40}{m}_{1}h+\frac{9}{40}{m}_{2}h,w_i+\frac{3}{40}{n}_{1}h+\frac{9}{40}{n}_{2}h,z_i+\frac{3}{40}{r}_{1}h+\frac{9}{40}{r}_{2}h\end{array}\right)\\ r_3=e\left(\begin{array}{l}{\eta }_i+\frac{3}{10}h,f_i+\frac{3}{40}{k}_{1}h+\frac{9}{40}{k}_{2}h,\text{}\text{}{p}_i+\frac{3}{40}{l}_{1}h+\frac{9}{40}{l}_{2}h,\\ q_i+\frac{3}{40}{m}_{1}h+\frac{9}{40}{m}_{2}h,w_i+\frac{3}{40}{n}_{1}h+\frac{9}{40}{n}_{2}h,z_i+\frac{3}{40}{r}_{1}h+\frac{9}{40}{r}_{2}h\end{array}\right)\end{array}$

$k_4=a\left(\begin{array}{l}{\eta }_i+\frac{3}{5}h,f_i+\frac{3}{10}{k}_{1}h-\frac{9}{10}{k}_{2}h+\frac{6}{5}{k}_{3}h,p_i+\frac{3}{10}{l}_{1}h-\frac{9}{10}{l}_{2}h+\frac{6}{5}{l}_{3}h,\\ q_i+\frac{3}{10}{m}_{1}h-\frac{9}{10}{m}_{2}h+\frac{6}{5}{m}_{3}h,w_i+\frac{3}{10}{n}_{1}h-\frac{9}{10}{n}_{2}h+\frac{6}{5}{n}_{3}h,\\ z_i+\frac{3}{10}{r}_{1}h-\frac{9}{10}{r}_{2}h+\frac{6}{5}{r}_{3}h\end{array}\right)$

$l_4=b\left(\begin{array}{l}{\eta }_i+\frac{3}{5}h,f_i+\frac{3}{10}{k}_{1}h-\frac{9}{10}{k}_{2}h+\frac{6}{5}{k}_{3}h,p_i+\frac{3}{10}{l}_{1}h-\frac{9}{10}{l}_{2}h+\frac{6}{5}{l}_{3}h,\\ q_i+\frac{3}{10}{m}_{1}h-\frac{9}{10}{m}_{2}h+\frac{6}{5}{m}_{3}h,w_i+\frac{3}{10}{n}_{1}h-\frac{9}{10}{n}_{2}h+\frac{6}{5}{n}_{3}h,\\ z_i+\frac{3}{10}{r}_{1}h-\frac{9}{10}{r}_{2}h+\frac{6}{5}{r}_{3}h\end{array}\right)$

$m_4=c\left(\begin{array}{l}{\eta }_i+\frac{3}{5}h,f_i+\frac{3}{10}{k}_{1}h-\frac{9}{10}{k}_{2}h+\frac{6}{5}{k}_{3}h,p_i+\frac{3}{10}{l}_{1}h-\frac{9}{10}{l}_{2}h+\frac{6}{5}{l}_{3}h,\\ q_i+\frac{3}{10}{m}_{1}h-\frac{9}{10}{m}_{2}h+\frac{6}{5}{m}_{3}h,w_i+\frac{3}{10}{n}_{1}h-\frac{9}{10}{n}_{2}h+\frac{6}{5}{n}_{3}h,\\ z_i+\frac{3}{10}{r}_{1}h-\frac{9}{10}{r}_{2}h+\frac{6}{5}{r}_{3}h\end{array}\right)$

$n_4=d\left(\begin{array}{l}{\eta }_i+\frac{3}{5}h,f_i+\frac{3}{10}{k}_{1}h-\frac{9}{10}{k}_{2}h+\frac{6}{5}{k}_{3}h,p_i+\frac{3}{10}{l}_{1}h-\frac{9}{10}{l}_{2}h+\frac{6}{5}{l}_{3}h,\\ q_i+\frac{3}{10}{m}_{1}h-\frac{9}{10}{m}_{2}h+\frac{6}{5}{m}_{3}h,w_i+\frac{3}{10}{n}_{1}h-\frac{9}{10}{n}_{2}h+\frac{6}{5}{n}_{3}h,\\ z_i+\frac{3}{10}{r}_{1}h-\frac{9}{10}{r}_{2}h+\frac{6}{5}{r}_{3}h\end{array}\right)$

$r_4=e\left(\begin{array}{l}{\eta }_i+\frac{3}{5}h,f_i+\frac{3}{10}{k}_{1}h-\frac{9}{10}{k}_{2}h+\frac{6}{5}{k}_{3}h,p_i+\frac{3}{10}{l}_{1}h-\frac{9}{10}{l}_{2}h+\frac{6}{5}{l}_{3}h,\\ q_i+\frac{3}{10}{m}_{1}h-\frac{9}{10}{m}_{2}h+\frac{6}{5}{m}_{3}h,w_i+\frac{3}{10}{n}_{1}h-\frac{9}{10}{n}_{2}h+\frac{6}{5}{n}_{3}h,\\ z_i+\frac{3}{10}{r}_{1}h-\frac{9}{10}{r}_{2}h+\frac{6}{5}{r}_{3}h\end{array}\right)$

$k_5=a\left(\begin{array}{l}{\eta }_i+h,f_i-\frac{11}{54}{k}_{1}h+\frac{5}{2}{k}_{2}h-\frac{70}{27}{k}_{3}h+\frac{35}{27}{k}_{4}h,p_i-\frac{11}{54}{l}_{1}h+\frac{5}{2}{l}_{2}h-\frac{70}{27}{l}_{3}h+\frac{35}{27}{l}_{4}h,\\ q_i-\frac{11}{54}{m}_{1}h+\frac{5}{2}{m}_{2}h-\frac{70}{27}{m}_{3}h+\frac{35}{27}{m}_{4}h,\text{}\text{}{w}_i-\frac{11}{54}{n}_{1}h+\frac{5}{2}{n}_{2}h-\frac{70}{27}{n}_{3}h+\frac{35}{27}{n}_{4}h,\text{}\\ z_i-\frac{11}{54}{r}_{1}h+\frac{5}{2}{r}_{2}h-\frac{70}{27}{r}_{3}h+\frac{35}{27}{r}_{4}h\end{array}\right)$

$l_5=b\left(\begin{array}{l}{\eta }_i+h,f_i-\frac{11}{54}{k}_{1}h+\frac{5}{2}{k}_{2}h-\frac{70}{27}{k}_{3}h+\frac{35}{27}{k}_{4}h,p_i-\frac{11}{54}{l}_{1}h+\frac{5}{2}{l}_{2}h-\frac{70}{27}{l}_{3}h+\frac{35}{27}{l}_{4}h,\\ q_i-\frac{11}{54}{m}_{1}h+\frac{5}{2}{m}_{2}h-\frac{70}{27}{m}_{3}h+\frac{35}{27}{m}_{4}h,\text{}\text{}{w}_i-\frac{11}{54}{n}_{1}h+\frac{5}{2}{n}_{2}h-\frac{70}{27}{n}_{3}h+\frac{35}{27}{n}_{4}h,\text{}\\ z_i-\frac{11}{54}{r}_{1}h+\frac{5}{2}{r}_{2}h-\frac{70}{27}{r}_{3}h+\frac{35}{27}{r}_{4}h\end{array}\right)$

$m_5=c\left(\begin{array}{l}{\eta }_i+h,f_i-\frac{11}{54}{k}_{1}h+\frac{5}{2}{k}_{2}h-\frac{70}{27}{k}_{3}h+\frac{35}{27}{k}_{4}h,p_i-\frac{11}{54}{l}_{1}h+\frac{5}{2}{l}_{2}h-\frac{70}{27}{l}_{3}h+\frac{35}{27}{l}_{4}h,\\ q_i-\frac{11}{54}{m}_{1}h+\frac{5}{2}{m}_{2}h-\frac{70}{27}{m}_{3}h+\frac{35}{27}{m}_{4}h,\text{}\text{}{w}_i-\frac{11}{54}{n}_{1}h+\frac{5}{2}{n}_{2}h-\frac{70}{27}{n}_{3}h+\frac{35}{27}{n}_{4}h,\text{}\\ z_i-\frac{11}{54}{r}_{1}h+\frac{5}{2}{r}_{2}h-\frac{70}{27}{r}_{3}h+\frac{35}{27}{r}_{4}h\end{array}\right)$

$n_5=c\left(\begin{array}{l}{\eta }_i+h,f_i-\frac{11}{54}{k}_{1}h+\frac{5}{2}{k}_{2}h-\frac{70}{27}{k}_{3}h+\frac{35}{27}{k}_{4}h,p_i-\frac{11}{54}{l}_{1}h+\frac{5}{2}{l}_{2}h-\frac{70}{27}{l}_{3}h+\frac{35}{27}{l}_{4}h,\\ q_i-\frac{11}{54}{m}_{1}h+\frac{5}{2}{m}_{2}h-\frac{70}{27}{m}_{3}h+\frac{35}{27}{m}_{4}h,\text{}\text{}{w}_i-\frac{11}{54}{n}_{1}h+\frac{5}{2}{n}_{2}h-\frac{70}{27}{n}_{3}h+\frac{35}{27}{n}_{4}h,\text{}\\ z_i-\frac{11}{54}{r}_{1}h+\frac{5}{2}{r}_{2}h-\frac{70}{27}{r}_{3}h+\frac{35}{27}{r}_{4}h\end{array}\right)$

$r_5=d\left(\begin{array}{l}{\eta }_i+h,f_i-\frac{11}{54}{k}_{1}h+\frac{5}{2}{k}_{2}h-\frac{70}{27}{k}_{3}h+\frac{35}{27}{k}_{4}h,p_i-\frac{11}{54}{l}_{1}h+\frac{5}{2}{l}_{2}h-\frac{70}{27}{l}_{3}h+\frac{35}{27}{l}_{4}h,\\ q_i-\frac{11}{54}{m}_{1}h+\frac{5}{2}{m}_{2}h-\frac{70}{27}{m}_{3}h+\frac{35}{27}{m}_{4}h,\text{}\text{}{w}_i-\frac{11}{54}{n}_{1}h+\frac{5}{2}{n}_{2}h-\frac{70}{27}{n}_{3}h+\frac{35}{27}{n}_{4}h,\text{}\\ z_i-\frac{11}{54}{r}_{1}h+\frac{5}{2}{r}_{2}h-\frac{70}{27}{r}_{3}h+\frac{35}{27}{r}_{4}h\end{array}\right)$

$k_6=a\left(\begin{array}{l}{\eta }_i+\frac{7}{8}h,f_i+\frac{1631}{55296}{k}_{1}h+\frac{175}{512}{k}_{2}h+\frac{575}{13824}{k}_{3}h+\frac{44275}{110592}{k}_{4}h+\frac{253}{4096}{k}_{5}h,\\ p_i+\frac{1631}{55296}{l}_{1}h+\frac{175}{512}{l}_{2}h+\frac{575}{13824}{l}_{3}h+\frac{44275}{110592}{l}_{4}h+\frac{253}{4096}{l}_{5}h,\\ q_i+\frac{1631}{55296}{m}_{1}h+\frac{175}{512}{m}_{2}h+\frac{575}{13824}{m}_{3}h+\frac{44275}{110592}{m}_{4}h+\frac{253}{4096}{m}_{5}h,\\ n_i+\frac{1631}{55296}{w}_{1}h+\frac{175}{512}{w}_{2}h+\frac{575}{13824}{w}_{3}h+\frac{44275}{110592}{w}_{4}h+\frac{253}{4096}{w}_{5}h,\\ z_i+\frac{1631}{55296}{r}_{1}h+\frac{175}{512}{r}_{2}h+\frac{575}{13824}{r}_{3}h+\frac{44275}{110592}{r}_{4}h+\frac{253}{4096}{r}_{5}h\end{array}\right)$

$l_6=b\left(\begin{array}{l}{\eta }_i+\frac{7}{8}h,f_i+\frac{1631}{55296}{k}_{1}h+\frac{175}{512}{k}_{2}h+\frac{575}{13824}{k}_{3}h+\frac{44275}{110592}{k}_{4}h+\frac{253}{4096}{k}_{5}h,\\ p_i+\frac{1631}{55296}{l}_{1}h+\frac{175}{512}{l}_{2}h+\frac{575}{13824}{l}_{3}h+\frac{44275}{110592}{l}_{4}h+\frac{253}{4096}{l}_{5}h,\\ q_i+\frac{1631}{55296}{m}_{1}h+\frac{175}{512}{m}_{2}h+\frac{575}{13824}{m}_{3}h+\frac{44275}{110592}{m}_{4}h+\frac{253}{4096}{m}_{5}h,\\ n_i+\frac{1631}{55296}{w}_{1}h+\frac{175}{512}{w}_{2}h+\frac{575}{13824}{w}_{3}h+\frac{44275}{110592}{w}_{4}h+\frac{253}{4096}{w}_{5}h,\\ z_i+\frac{1631}{55296}{r}_{1}h+\frac{175}{512}{r}_{2}h+\frac{575}{13824}{r}_{3}h+\frac{44275}{110592}{r}_{4}h+\frac{253}{4096}{r}_{5}h\end{array}\right)$