The purpose of this paper is to investigate the effect of using a convergent hot tube on the vortex tube refrigeration capacity. The computational fluid dynamics (CFD) model used is a three-dimensional steady compressible model that utilizes the k-ɛ turbulence model. In this numerical research, different convergence angles of the hot tube (β=0˚, 0.5˚, 0.88˚, 1˚, 1.5˚, and 2˚) have been considered to analyze the vortex tube performance. The results showed that as the angle converges from the cylindrical model (β=0˚), the cold temperature separation improves at the cold mass fractions greater than about 0.3, but increasing the angle more than 2˚ impairs the cold temperature separations compared to the cylindrical model, because of the secondary circulation development inside the vortex tube. Also, a successful validation has been carried out between some available experimental results and the present numerical model (for cylindrical vortex tube) Table 1.

The vortex tube is a simple device, without any moving parts, that separates a pressurized flow of air (or any inlet gas) into hot and cold streams. Compressed air enters tangentially into the vortex chamber, where it splits into two lower pressure streams, the peripheral and the inner vortexes. The hot stream rotates near the outer radiuses (near the wall) while the cold stream flows at the center of the tube. The hot outer layers of the compressed gas escape through the conical valve side at the end of the tube. The remaining gas returns in an inner vortex and leaves through the cold exit orifice located at the other end of the tube near the inlets. This behavior is schematically illustrated in Figure 1. There are various explanations for this behavior happened in the vortex tubes. One explanation is that, owing to centrifugal force, the outer air is under higher pressure than the inner air. So, the temperature of the outer layers is higher than that of the inner layers. Another explanation is that as both vortices have the same angular velocity and direction, the inner vortex loses angular momentum. This decrease in angular momentum is transferred to the outer vortex as kinetic energy, resulting in the separation phenomenon inside the chamber.

Figure 1 Schematic drawing of a vortex tube operational mechanism.

French physicist Ranque¹invented the vortex tube in 1933.¹ Later, a German physicist² improved the design and published a widely read paper in 1947 regarding the device. So, this device is known as the Ranque-Hilsch vortex tube, as well. Although the device is geometrically simple, the phenomenon occurring in the tube is quite complex. A great amount of research has been dedicated to understanding the energy separation phenomenon in the Ranque Hilsch1 vortex tube. Kurosaka³ stated that the temperature separation is a result of the acoustic streaming effect. Stephan et al.⁴ maintained that Gortler vortices form on the inside wall of the tube and drives the fluid motion. An imbedded secondary circulation was discussed by Ahlborn & Gordon.⁵ A CFD model of the vortex tube was employed by Aljuwayhel et al.⁶ to understand the fundamental processes that cause the power separation inside the vortex tube. Behera et al.⁷ investigated the effect of the number of nozzles on energy separation both experimentally and using numerical CFD models. Skye et al.⁸ made a comparison between the performance predicted by a computational fluid dynamic (CFD) model and their experimental measurements using an available commercial vortex tube. Chang et al.⁹ used the surface tracing method to carry out some experimental tests on the internal flow phenomena and to show the stagnation point position in a vortex tube. Eiamsa-ard & Promvonge¹⁰ utilized a CFD model to investigate the flow field and the temperature separation behavior. Pinar et al.¹¹ used the Taguchi method to obtain the optimal number of nozzles for the vortex tube. Xue et al.¹² studied pressure gradient, viscosity and turbulence, secondary circulation, and acoustic streaming in the vortex tube. Shamsoddini & Hossein Nezhad¹³ analyzed the flow and heat transfer mechanism in the vortex tube using a three-dimensional CFD model. In order to investigate the variation of velocity, pressure, and temperature inside a vortex tube, Akhesmeh et al.¹⁴ developed a three-dimensional CFD model. Bramo & Pourmahmoud15 numerically examined the effect of length-to-diameter ratio (L/D) and stagnation point position on the temperature separation. Pourmahmoud et al.^16,17 analyzed the effect of number and shape of nozzles on the vortex tube behavior. They found that applying the helical nozzles leads to higher swirl velocity and temperature difference, as compared to the straight nozzles. Earlier research showed that using a divergent hot tube improves the cooling performance of the vortex tube as compared to the cylindrical one. Raiskii & Tankel¹⁸ conducted an experimental study on the energy separation of a typical vortex tube using a divergent piece to form a part of the hot tube and reported that the typical vortex tube could improve the performance of the cylindrical one. Gulyaev et al.¹⁹ found that replacing the cylindrical hot tube with a 2.3° divergent hot tube enhances the refrigeration capacity of the device. Takahama & Yokosowa²⁰ employed a divergent hot tube and report edits cooling performance to be higher than that of the cylindrical one with the same lengths. Chang et al.²¹ investigated the effect of divergent hot tube on the temperature separation, experimentally and found that the divergent vortex tube equipped with the divergent main tube with divergence angle of 4° provides the highest temperature reduction. They reported that any increase or decrease in this critical angle causes a sensitive decrease in the cooling performance of the vortex tube.

It should be said that the effect of convergent main tube on the thermal performance of vortex tube is not analyzed yet (Experimental or numerical).

In this paper, the numerical study focuses on description of the effect of convergent hot tube on the temperature separation inside the vortex tube. A numerical simulation is carried out to obtain the specified range of angles that improves the cooling performance of the convergent vortex tube. For this purpose, the CFD models were created and analyzed by the fluent commercial software (Fluent 6.3.26) and the results were presented as the exit temperatures and the flow field patterns.

The CFD model used in this study is based on the experimental model that is employed by Skye et al.⁸ It should be mentioned that the device used by Skye et al.⁸ was an ExairTM 708 slpm vortex tube. The geometrical properties of the device are provided in Table 2. The nozzle of the vortex tube includes six straight slots. In their work, Skye et al.⁸ also numerically analyzed the vortex tube behavior using a two-dimensional (2D) model. However, the complex compressible turbulent flow inside the vortex tube motivated us to arrange some numerical studies using 3D models.

The model used in the present study simulates a vortex tube having the same geometrical properties as that used in Skye et al.⁸ experimental research. In order to reduce the computation costs, only a 60° sector of the convergent vortex tube is considered as the computational domain, so, the models are assumed as a domain with rotational periodic condition Figure 2.

The boundary conditions in this numerical work are based on the experimental measurements in the mentioned experimental work Skye et al.⁸ as follows:

1. At the nozzle inlets, compressed air is modeled as mass flow inlet, with specified total mass flow rate of 8.35 gr s-1 and the stagnation temperature fixed at 294.2 K.
2. The air flow is considered as an ideal, fully turbulent and compressible gas flow. The static pressure at the cold exit boundary was fixed at experimental measurements (0.15 bar absolute).
3. The static pressure at the hot exit boundary is adjusted in the way to vary the cold mass fraction. Since the CFD model predicts that the reversed flows will occur at the cold exit (at low cold gas fractions), so the backflow temperature value is fix at 290 K.
4. The tube walls are considered as the adiabatic surfaces and the no slip conditions are used.
5. Boundary conditions are kept same for all models throughout the analysis. The pressure-outlet boundary condition is used when the outlet pressures are known.

The flow streams are considered to be compressible and turbulent, for which the standard k-ɛ turbulence model is employed. The renormalization group (RNG) k-ɛ turbulence model and the Reynolds stress equations were examined, as well. However, these two models could not be made to converge for this simulation. Bramo & Pourmahmoud¹⁵ stated that the k-ɛ model is preferred to simulate the turbulent pattern inside the vortex tube, since its numerical results exhibit a better agreement with the experimental data. The governing equations for fluid flow are as follows:

-Continuity equation

  $\frac{\partial }{\partial x_j}(\rho u_j)=0$ …………….. (1)

-Momentum equation

   $\frac{\partial }{\partial {{\displaystyle x}}_j}(\rho {{\displaystyle u}}_i{{\displaystyle u}}_j)=-\frac{\partial p}{\partial {{\displaystyle x}}_i}+\frac{\partial }{\partial {{\displaystyle x}}_j}\left[\mu \left(\frac{\partial {{\displaystyle u}}_i}{\partial {{\displaystyle x}}_j}+\frac{\partial {{\displaystyle u}}_j}{\partial {{\displaystyle x}}_i}-\frac{2}{3}{\delta }_{ij}\frac{\partial {{\displaystyle u}}_k}{\partial {{\displaystyle x}}_k}\right)\right]+\frac{\partial }{\partial {{\displaystyle x}}_j}(-\overline{\rho }{\overline{u^{\prime }}}_i{\overline{u^{\prime }}}_j)$ ………. (2)

Energy equation

  $\frac{\partial }{\partial {{\displaystyle x}}_i}\left[{{\displaystyle u}}_i\rho \left(h+\frac{1}{2}{{\displaystyle u}}_j{{\displaystyle u}}_j\right)\right]=\frac{\partial }{\partial {{\displaystyle x}}_j}\left[{{\displaystyle k}}_{eff}\frac{\partial T}{\partial {{\displaystyle x}}_j}+{{\displaystyle u}}_i{({{\displaystyle \tau }}_{ij})}_{eff}\right]$ $k_{eff}=K+\frac{{{\displaystyle c}}_p{{\displaystyle \mu }}_t}{{{\displaystyle \mathrm{Pr}}}_t}$ ……….. (3)

As the working fluid is assumed to be an ideal gas, the state equation is necessary to show the compressibility effect, which is as follows:

$p=\rho RT$ ………(4)

The turbulence kinetic energy (k) and the rate of dissipation (ε) are obtained from the following equations:

$\frac{\partial }{\partial t}(\rho k)+\frac{\partial }{\partial {{\displaystyle x}}_i}(\rho k{u}_i)=\frac{\partial }{\partial {{\displaystyle x}}_j}[(\mu +\frac{{{\displaystyle \mu }}_t}{{{\displaystyle \sigma }}_k})\frac{\partial k}{\partial {{\displaystyle x}}_j}]+{{\displaystyle G}}_k+{{\displaystyle G}}_b-\rho \epsilon -{{\displaystyle Y}}_M$ ………. (5)

$\frac{\partial }{\partial t}(\rho \epsilon )+\frac{\partial }{\partial {{\displaystyle x}}_i}(\rho \epsilon {{\displaystyle u}}_i)=\frac{\partial }{\partial {{\displaystyle x}}_j}[(\mu +\frac{{{\displaystyle \mu }}_t}{{{\displaystyle \sigma }}_{\epsilon }})\frac{\partial \epsilon }{\partial {{\displaystyle x}}_j}]+C_{1\epsilon }\frac{\epsilon }{k}(G_k+C_3{}_{\epsilon }{G}_b)-C_{2\epsilon }\rho \frac{{\epsilon }^2}{k}$ ……..(6)

Where Gk, Gb, and YM represent the generation of turbulent kinetic energy due to the mean velocity gradients, the generation of turbulent kinetic energy due to the buoyancy effect, and the contribution of the fluctuating dilatation in the compressible turbulence to the overall dissipation rate, respectively. Also, C1ɛ and C2ɛ are constants. These default values have been determined from the experiments with air and water for fundamental turbulent shear flows including homogeneous shear flows and decaying isotropic grid turbulence. They have been found to work fairly well for a wide range of wall-bounded and free shear flows. σk and σɛ are the turbulent Prandtl numbers for k and ɛ. The turbulent viscosity, μt, is computed as follows:

${{\displaystyle \mu }}_t=\rho {{\displaystyle C}}_{\mu }\frac{{{\displaystyle k}}^2}{\epsilon }$ ……..(7)

Where Cμ is a constant. The model constants C1ε, C2ε, Cμ, σk, and σε have the following default values: C1ε = 1.44, C2ε = 1.92, Cμ = 0.09, σk = 1.0, σε = 1.3.The Finite Volume Method (FVM) with a 3D structured mesh is applied to solve the governing equations, which is one of the numerical approaches to describe the complex flow patterns in the vortex tube. Inlet air is considered as a compressible working fluid, where its specific heat, thermal conductivity and dynamic viscosity are taken to be constant during the numerical analysis procedure. The second order upwind scheme is utilized to discretize the convective terms, and the SIMPLE algorithm is used to solve the momentum and energy equations simultaneously. Because of highly non-linear and coupling virtue of the governing equations, lower under-relaxation factors ranging from 0.1 to their default amount are taken for the pressure, density, body forces, momentum, k, ɛ , turbulent viscosity and energy components to ensure the stability and the convergence of the iterative calculations.

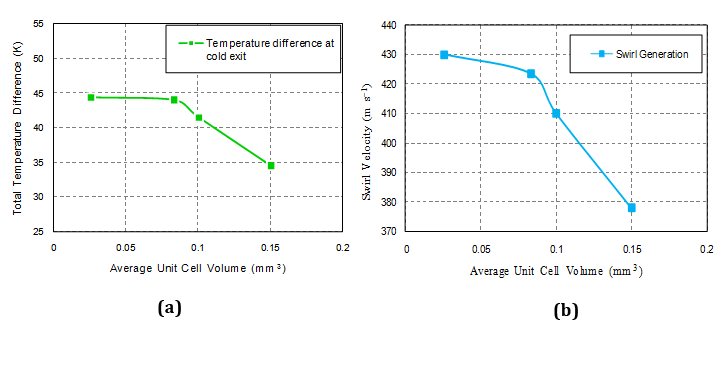
Grid independency

In order to show the grid independency of the results, different average unit cell volumes in the model have been analyzed. Two main studied parameters are the variation of total temperature difference and the maximum swirl velocity, as shown in Figure 3. Decreasing the unit cell volume size below 0.0257 mm3, corresponding to 0.287 million cells, does not result in a considerable difference in the mentioned parameters.

Figure 3 Grid size dependence on a) total temperature difference and b) maximum swirl velocity at different average unit cell volumes.

Validation

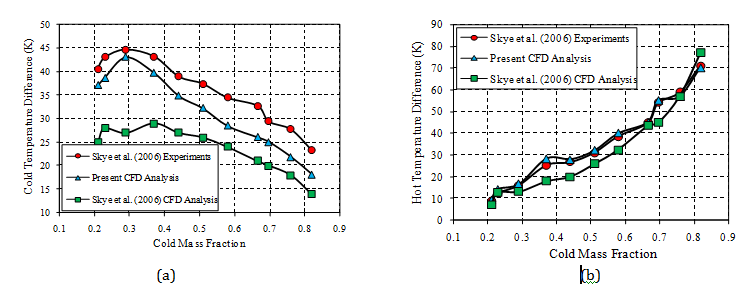
The temperature separation results obtained from CFD simulations are compared with the experimental results Skye et al.⁸ as shown in Figure 4(a) exhibits the good agreement between the predicted cold temperature difference (ΔTi,c) and the Skye et al.’s⁷ results. As compared to Skye et al.⁸ computational results (2D modeling), the present results (3D modeling) were closer to the experimental results. In the case of the hot temperature separation (ΔTi,h), the predicted values of both Skye et al.⁸ and the present study are very close to the experimental results, as displayed in Figure 4(b). The maximum ΔTi,c is obtained at the cold mass fraction of about 0.3 in both experiment and the CFD modeling. An increase in the cold mass fraction leads to an increase in the hot exit temperature difference. At the cold mass fraction of 0.81, the maximum hot exit temperature difference was observed.

Figure 4 Comparison of the present CFD model and the experimental results with regard to a) cold temperature difference and b) hot temperature difference.

Cylindrical vortex tube investigation

The CFD analysis has been conducted to investigate the variation of velocity components, total pressure, and total temperature on the radial profiles at three axial locations (Z/L= 0.1, 0.4, 0.7) at the cold mass fraction of 0.3 to analyze the flow characteristics within the cylindrical vortex tube. In Figure 5 & 6, the radial profiles for the swirl and axial velocities at Z/L= 0.1, 0.4, and 0.7 are provided. It can be observed that the swirl velocity has greater magnitude than the axial velocity. According to these figures, the magnitudes of swirl and axial velocities decrease rapidly as we move from the inlet to the hot outlet. The radial profile of swirl velocity indicates a free vortex near the wall. On the other hand, the second or forced vortex is formed in the core which is consistent with the results reported by Kurosaka³ and Gutsol.²² Also, the profiles obtained for the swirl and axial velocities (at different axial locations)are in good agreement with the observations of Gutsol²² and Behera et al. ⁷

Figure 5 Radial profile of swirl velocity at different axial locations for α=0.3.

Figure 6 Radial profile of axial velocity at different axial locations for α=0.3.

The total temperature variations at three axial locations Z/L= 0.1, 0.4, and 0.7are presented in Figure 7. The figure shows that the maximum total temperature occurred near the walls. Also, the low temperature zone in the core coincides with the negligible swirl velocity zone. Figure 8 shows the total pressure variations at three axial locations Z/L= 0.1, 0.4 and 0.7. The total pressure increases in all Z/L cross-sections as shown in Figure 8. So, the maximum total pressure is observed near walls and the minimum occurs in the central layers. The pressure difference between the peripheral layers and the central layers decreases as distance from the inlet increases.

Figure 7 Radial profile of total temperature at different axial locations for α=0.3.

Figure 8 Radial profile of total pressure at different axial locations for α=0.3.

The contours of total temperature distribution sat the cold mass fraction of 0.3 in the case of cylindrical vortex tube are displayed in Figure 9. It can be clearly seen that the peripheral flow is warm and the central flow is cold. Furthermore, increase of temperature is observed in the radial direction. For the cold mass fraction of about 0.3, the cylindrical vortex tube gives the maximum hot temperature of 311.5 K and the minimum cold temperature of 250.24 K.

Figure 9 Contours of total temperature at Z/L=0.1, Z/L=0.4, Z/L=0.7.

The effect of convergent hot tube             

The geometrical parameters of the vortex tube affect its cooling performance. Many researchers investigated the effect of shape and number of inlet nozzles, the length and diameter of the working tube, etc. One of the significant geometrical parameters that its effect on the thermal separations inside the vortex tube has not been studied yet is the convergence angle of the hot tube. In order to investigate the effect of using a convergent hot tube (compared to straight one) on the vortex tube thermal performance, the above-mentioned simulated model has been utilized. All parameters, except the convergence angle have been kept constant. The angle β is defined as the deviation from the cylindrical model (β= 0˚) as shown in Figure 10.

Figure 10: Schematic of vortex tube with convergent hot tube.

To examine the effect of the convergence hot tube, some main tubes with small degrees (β=0˚, 0.5˚, 0.88˚, 1˚, 1.5˚, and 2˚) were simulated. The cold temperature differences for different cold mass fractions, i.e., 0.2 to 0.82 are presented in this figure for the mentioned range of angles. These numerical results are depicted in Figure 11 & 12. Figure 11 shows that the maximum cold temperature difference occurs at the cold mass fraction of 0.3 in the cylindrical model (β= 0˚). Also, it can be said that by converging the vortex tube, the cooling performance of the vortex tube improves as compared to the straight one (β= 0˚) at the cold mass fractions greater than about 0.3.For β=1.5˚ the machine acts only for α≥0.65 and for cold mass fractions (α) smaller than 0.65 the flow separation does not appear in the vortex tube. For this angle, the maximum cold temperature difference is achieved. These results can be elucidated on basis of the statements by Shannak ²³ as follows: at the cold mass fractions higher than 0.4, the energy separation performance is based on the dominant role of viscous resistance, friction and the secondary circulation. However for 0.4 ≤ α ≤ 0.65, the vortex tube with the convergent angle of 2˚ is suitable for the cooling purposes. In fact, the convergence angle reduces the swirling velocity of the gas stream in the hot tube and leads to a decrease in the friction loss and the internal viscous loss, which creates an increase in the energy separation quality. But, when the convergence angle of hot tube increases more, the secondary circulation flow will develop in the tube, which causes a decrease in the temperature separation. At the cold mass fractions lower than 0.3, the energy separation performance is based on the more dominant role of swirl velocity. In this range of cold mass fractions, the swirl velocity is large enough to overcome the viscous resistance. Therefore, the cylindrical model with the largest swirl velocity exhibits the maximum cold temperature difference.

Figure 11: Influence of the angle of convergent hot tube on the cold temperature difference.

Figure 12 Influence of the angle of convergent hot tube on the hot temperature difference.

As Figure 12 illustrates; the vortex tube with β=0.5˚ produces the maximum hot exit temperature difference at the most of cold mass fractions (α). Therefore, it is recommended to use this angle when the hot exit temperature is considered. However, the vortex tube is often used for cooling applications not heating, so the cold exit temperature data are more important rather than hot exit temperature.

Stephan et al.⁴ carried out an approximate investigation for geometrically similar vortex tubes with straight nozzles and reported that the ratio of the actual temperature drop of the cold gas that exits from the exhaust to the maximum temperature difference(ΔTc/ΔTc,max) can be defined as a function of cold mass fraction as below:

$\frac{\Delta T_c}{\Delta T_{c,\max }}=f(\alpha )$ ……….. (8)

In this equation, ΔT_c,max is the maximum temperature drop and α is varied in the range of 0.2 to 0.82. The similarity relation DTc/DTc,max as a function of α can be taken and indicated. It can be introduced as below:

$\frac{\Delta T_c}{\Delta T_{c,\max }}=\text{-320}\text{.83}{\alpha }^{\text{6}}\text{ + 1032}\text{.1}{\alpha }^{\text{5}}\text{ - 1341}\text{.2}{\alpha }^4\text{ + 896}\text{.25}{\alpha }^3\text{ - 324}\text{.09}{\alpha }^2\text{ + 59}\text{.611}\alpha \text{ - 3}\text{.3356}$ ……….(9)

To confirm the similar relation for our vortex tube with convergent main tube, results by Hilsch,² Stephan et al.⁴ and Rafiee & Rahimi²⁴ are applied to compare and the results of this comparison is presented in Figure 13.

Figure 13 Comparison of similarity relations obtained by different works.

In addition, the flow patterns as path lines at sectional lengths near the cold and hot exits also the middle region are shown in Figure 14. The formation of core and peripheral streamlines can be clearly seen near the cold end and the middle region, but after the separation phenomenon the core vortex is disappeared. In spite of creating of such reversed flow, the peripheral flow does not alter its continuation towards the hot end. It should be said that, the axial distance between the stagnation point and the hot exit is too short.

Figure 14 3D Path lines colored by total temperature along the vortex tube.

The path lines help to realize the flow patterns, so that all symmetrical flow fields can be identified as well as various hot and cold flow regions.

 Approaching to a properly symmetric rotating flow and effective intensively domain. In order to demonstrate the effect of divergence angle on the radial profiles of the swirl velocity, the profiles at three axial locations (Z/L= 0.1, 0.4, 0.7) at the cold mass fraction of 0.4 were analyzed and the diagrams of which are depicted in Figure 15. The diagrams show that the swirl velocity of the gas stream for β=2˚ has the highest amount as compared to other models. Also, the swirl velocity decreases for all angles, as we move towards the hot exit. In Figure 16, the radial profiles of the axial velocities at Z/L= 0.1, 0.4, and 0.7 are provided at the cold mass fraction of 0.4. It can be observed that the axial velocity has a lower magnitude than the swirl velocity. Moreover, both velocity components of the stream decrease as they move toward the hot end side.

The total pressure counters at the longitudinal section of the vortex tube with β = 1˚ are shown in Figure 17. According to Figure 17, by moving air toward the hot end, the periphery total pressure decreases. The pressure of core flow decreases from the hot to the cold end and the minimum pressure occurs at the vortex tube cold exit. A considerable percentage of the expansion appears at the nozzles exit that can be one of the parameters to explain the temperature separation phenomena in the vortex tube. The static pressure does not change much along the tube Figure 18. The total pressure matches to the static pressure along the tube but attains a higher value than the static pressure toward the exit due to the increase in the velocity.

Figure 15 Radial profile of swirl velocity at different axial locations for α=0.4.

Figure 16 Radial profile of axial velocity at different axial locations for α=0.4.

Figure 17 Total pressure counter for β = 1˚ and α=0.4.

Figure 18 Static pressure counter for β = 1˚ and α=0.4.

In this study, a 3D CFD model was created to analyze the temperature separation inside a cylindrical vortex tube. This model is based on the experimental study by Skye et al.8 The simulation was developed using a three-dimensional and steady model that utilizes the standard k-ɛ turbulence equations. There is good agreement between the CFD results and the measured experimental data. The numerical model is capable of obtaining the swirl and axial velocity components, which are difficult to obtain experimentally. The analysis showed that the maximum ΔTi,c is obtained at the cold mass fraction of about 0.3 and the maximum ΔTi,h was observed at the cold mass fraction of 0.8 in both experimental and the CFD model. According to these results, the swirl velocity magnitude is higher than axial and radial velocities.

In addition, the effect of using a convergent hot tube on the energy separation in a vortex tube was analyzed, where all the parameters were kept constant except for the convergence angle. The numerical results indicated that the cooling performance of the vortex tube can be improved utilizing a convergent hot tube at the cold mass fractions higher than 0.4. However, this improvement can be achieved as long as the divergence angle does not exceed 2°.

None.

The author declares no conflict of interest.

1. Ranque GJ. Experiments on expansion in a vortex with simultaneous exhaust of hot air and cold air. J Phys Radium. 1933;4:112–115.
2. Hilsch R. The use of expansion of gases in a centrifugal field as a cooling process. Rev Sci In strum. 1947;18:108–113.
3. Kurosaka M. Acoustic streaming in swirling flows. J Fluid Mech. 1982;124:139–172.
4. Stephan K, Lin S, Durst M, et al. An investigation of energy separation in a vortex tube. Int J Heat Mass Transfer. 1983;26:341–348.
5. Ahlborn BK, Gordon JM. The vortex tube as a classic thermodynamic refrigeration cycle. J Appl Phys. 2000;88(6):3645–3653.
6. Aljuwayhel NF, Nellis GF, Klein SA. Parametric and internal study of the vortex tube using a CFD model. Int J Refrigeration. 2005;28(3):442–450.
7. Behera U, PJ Paula, S Kasthurirengan, et al. CFD analysis and experimental investigations towards optimizing the parameters of Ranque–Hilsch vortex tube. Int J Heat Mass Transfer. 2005;48:1961–1973.
8. Skye HM, Nellis GF, Klein SA. Comparison of CFD analysis to empirical data in a commercial vortex tube. Int J Refrigeration. 2006;29(1):71–80.
9. Chang HS, Chang SK, Ui HJ, et al. Experimental and Numerical Studies in a Vortex Tube. J Mech SciTech. 2006;20(3):418–425.
10. Eisma–ard S, Promvonge P. Numerical investigations of the thermal separation in a Ranque–Hilsch vortex tube. Int J Heat Mass Transfer. 2007;50(5–6):821–832.
11. Pinar AM, Uluer O, Kirmaci V. Optimization of counter flow Ranque–Hilsch vortex tube performance using Taguchi method. Int J Refrigeration. 2009;32(6):1487–1494.
12. Xue Y, Ajormandi M, Kelso R. A critical review of temperature separation in a vortex tube. J Exp Therm Fluid Sci. 2010;34(8):1367–1374.
13. Shamsoddini R, Hossein Nezhad A. Numerical analysis of the effects of nozzles number on the flow and power of cooling of a vortex tube. Int J Refrigeration. 2010;33(4):774–782.
14. Akhesmeh S, Pourmahmoud N, Sedgi H. Numerical study of the temperature separation in the Ranque–Hilsch vortex tube. Am J Eng Appl Sci. 2008;3:181–187.
15. Bramo AR, Pourmahmoud N. CFD simulation of length to diameter ratio effect on the energy separation in a vortex tube. Therm Sci. 2011. 15:833–848.
16. Pourmahmoud N, Hassan Zadeh A, Moutaby O, et al. Computational fluid dynamics analysis of helical nozzles effects on the energy separation in a vortex tube. Therm Sci. 2012;16:151–166.
17. Pourmahmoud N, Hassan Zadeh A, Moutaby O. Numerical analysis of the effect of helical nozzles gap on the cooling capacity of Ranque–Hilsch vortex tube. Int J Refrigeration. 2012;35(5):1473–1483.
18. Raiskii YD, Tankel LE. Influence of vortex–tube saturation and length on the process of energetic gas separation. J Eng Phys. 1974;27(6):1578–1581.
19. Gulyaev AI. Investigation of conical vortex tubes. J Eng Phys. 1966;10(3):193–195.
20. Takahama H, Yokosawa H. Energy separation in vortex tube with a divergent chamber. J Heat Transfer. 1981;103(2):196–203.
21. Chang K, Li Q, Zhou G, et al. Experimental investigation of vortex tube refrigerator with a divergent hot tube. Int J Refrigeration. 2011;34(1):322–327.
22. Gutsol AF. The Ranque effect. Phys Uspekhi. 1972;40(6):639–658.
23. Shannak BA. Temperature separation and friction losses in vortex tube. Heat Mass Transfer. 2004;40(10):779–785.
24. Rafiee SE, Rahimi M. Experimental study and three–dimensional (3D) computational fluid dynamics (CFD) analysis on the effect of the convergence ratio, pressure inlet and number of nozzle intake on vortex tube performance–Validation and CFD optimization. Energy. 2013;63:195–204.