Bunsen reaction () is a center reaction $2H_{2}O+I_2+S{O}_2\to H_{2}S{O}_4+2HI$ of two important chemical cycles for hydrogen production: the H₂S splitting cycle and the sulfur-iodine (S-I) water-splitting cycles. Introducing I₂-tolune solution to the reaction can ease challenges such as side reactions and corrosion hazard. The glass-made Corning^® Advanced-Flow^TM Reactor (AFR) can completely avoid corrosion and also improve the mass transfer among the multiphase, i.e., gas SO₂-N₂, water, and toluene-I₂, to produce HI/H₂SO₄. In this paper, the absorption behavior of SO₂ in water, toluene and water-toluene mixture was investigated in the absence of iodine. The influences of mole fraction of SO₂ in gas phase and the flow rates of gas and liquid on SO₂ absorption rate and liquid-side volumetric mass transfer coefficients showed different absorption behaviors of SO₂ molecules in water and toluene. The differences also appeared between the microscale and milliscale AFR. However, the plot of the liquid-side volumetric mass transfer coefficient vs. residence time indicated straightforward and seamless scalability of the AFR from microscale to milliscale for SO₂-water and SO₂-toluene absorption. This absorption study was necessary to provide preliminary data for the multiphase Bunsen reaction study in which iodine is present.

Keywords: bunsen reaction, H₂S splitting cycle, hydrogen production, corning^® glass advanced-flow^TM reactor, liquid-side volumetric mass transfer coefficient

To upgrade bitumen from Canadian oil sands into synthetic crude oil, a tremendous amount of hydrogen (H₂) is needed mostly for hydrotreating, where nearly the same amount of hydrogen sulfide (H₂S) is produced on molar basis. Traditionally, the H₂S is converted into elemental sulfur (S) in sulfur recovery units through the Claus process.¹ Although the Claus process is very well established, it has drawbacks. For instance, about half of the H₂S handling costs are related to the tail gas treatment. More importantly, the conversion of hydrogen into low-value water reduces plant efficiency. An H₂S chemical splitting cycle2was developed in our research group in order to directly decompose hydrogen sulfide with simultaneous production of hydrogen, which could be reused in oil sands upgrading as a partial substitute for steam reforming of methane (SRM). Similar to the S-I water-splitting cycle,³ this cycle consists of three chemical reactions:

$H_{2}S+H_{2}S{O}_4\to S+S{O}_2+2H_{2}O\left(120–{150}^{o}C\right)$

$2H_{2}O+I_2+S{O}_2\to H_{2}S{O}_4+2HI\left({25}^{o}C\right)$ (2)

$2HI\to H_2+I_2\left({25}^{o}C\right)$(3)

The overall reaction is:

$H_{2}S\to H_2+S$ (4)

By further oxidizing the elemental sulfur produced from reaction (1) into SO₂, the cycle can produce two moles of H₂ from one mole of H₂S, leading to the production of one mole of sulfuric acid.² Reaction (2), known as the Bunsen reaction, and reaction (3), known as HI decomposition, are two of the three reactions in the S-I water-splitting cycle. These reactions have been widely studied since the S-I cycle was proposed, in particular, the Bunsen reaction, which links the sulfur and iodine loops in the S-I water-splitting cycle, has received remarkable attention recently through massive investments in research.^4–6 Initially, General Atomics (GA) proposed the following stoichiometry:

$S{O}_2+16H_{2}O+9I_2\to {\left(2HI+10H_{2}O+8I_2\right)}_{HIxphase}+{\left(H_{2}S{O}_4+4H_{2}O\right)}_{sulfuricacidphase}$                                                                                                                                                                                               (5)

Where, a large amount of iodine and water is required to prevent side reactions³ and to separate the two acid products into two immiscible liquid phases: sulfuric acid (upper phase), mainly a mixture of H₂SO₄ and water, and hydroiodic acid (lower phase), including HI, I₂, and water.⁷ Excessive use of water and iodine, according to the stoichiometry of reaction (5), results in increased capital and operating costs because of the excessive material circulation and reduced energy efficiency of the entire chemical cycle. For instance, high heat duty is required for the concentration of both acids prior to decomposition.⁶ In addition, the Bunsen reaction must be carried out at elevated temperatures above the melting point of iodine (117^°C), leading to iodine vapor deposition in the setup and tube blockage. At the elevated temperatures, the severe corrosive of the Bunsen reaction products is also a major concern.⁸ Therefore, experimental and theoretical research activities have been carried out during the last decade to minimize Bunsen reaction challenges.^9‒12 Our research group recently proposed a low-temperature process for the H₂S splitting cycle where toluene is used to simply dissolve iodine and this dissolved iodine can be transported from I₂-toluene solution to aqueous phase such that the Bunsen reaction can be carried out continuously at room temperature.¹³

This low-temperature process avoids the side reactions and iodine vapor deposition, and prevents corrosion. Subsequent electrolysis of the Bunsen reaction products relieves concerns about product acids separations as well. Despite all the benefits, the use of an I₂-toluene solution leads to a multiphase reaction system involving gas, aqueous, and organic solutions, denoted as a gas-liquid-liquid system. In the multiphase reaction system, mass transfer across phases may become rate-limiting. The overall rate is proportional to the liquid-side volumetric or overall mass transfer coefficient (K_La). Usually, generation of high shear in the liquid near the interface and large interfacial areas are desirable in order to achieve high mass transfer rates.¹⁴ Therefore, the apparent reaction rate of the Bunsen reaction was studied in the gas-liquid-liquid multiphase system using a batch reactor.¹⁵ Comparisons of the rate of SO₂ absorption in the liquids of different compositions (toluene, toluene and water, I₂-toluene solution, water), indicated that SO₂ dissolution in liquid phase was the rate-controlling step provided the gas phase resistance was negligible. This was confirmed by the small value of the activation energy (6.02kJ mol^-1) obtained by fitting the reaction rate at various temperatures using the Arrhenius equation. It was concluded that improvement of cross-phase mass transfer is critical to increase process efficiency.

The emerging new reactor technology, Corning^® Advanced-Flow^TM Reactor, was claimed to be capable of improving the gas-liquid mass transfer coefficients compared to other gas-liquid contactors such as bubble columns and spray columns.¹⁶ The AFR are made of glass or ceramic materials that are highly corrosion-resistant for aqueous acid solutions. The modular design of these AFR allows scale-up from the lowest flow rate (10mL min^-1) of the low-flow (LF) cells to highest flow rate (5000mL min^-1) of the G4 cells. In addition, AFR can improve heat transfer effectively.^17‒19 To investigate the gas-liquid-liquid multiphase system of the Bunsen reaction where I₂ was provided for the Bunsen reaction through I₂-toluene solution, two types of AFR, AFR-LF (maximum through-put: 5m³/year) and AFR-G1 (maximum through-put: 80m³/year), were chosen. The work is reported under one general title, divided into part one and part two. Part one, the present paper, deals with the absorption of SO₂ in water, toluene and water-toluene mixture to study the behaviors of multiphase system in the absence of iodine (Bunsen reaction). By applying two-film theory, the liquid-side volumetric mass transfer coefficients were calculated for the binary systems. The results for the two scales of AFR (LF and G1) were also compared. With iodine added to SO₂-water-toluene mixture, part two studied the effects of operating conditions such as gas and liquid flow rates, water-to-toluene ratio, and temperature on SO₂ absorption and of I₂ consumption in continuous mode in both LF and G1.

The experiment with the AFR-LF was conducted and analyzed at the University of Saskatchewan (UofS). The experiment using the AFR-G1, a larger commercially available module, was performed at the Corning Reactor Technology Center (CRTC) in Changzhou, China, while the analyses were performed in the Department of Biochemical Engineering, Changzhou University, Changzhou, China.

1. Experimental setups and operating conditions

The flow pathway of the AFR consists of identical small heart-shaped cells in blue color as shown in Figure 1. Each module has variable cross sections, which cause the fluid to form a jet and repeat splitting and mixing actions along the pathway (divergent-convergent configuration).¹⁶ This mechanism helps to increase the contact area among the phases. Commercial AFR are designed in different sizes (LF, G1, G2, G3, and G4) depending on the state of the research and/or the scale of production throughput. The interconnected fluidic module design allows the use of several modules in cascades for multiple-step reactions. Each glass module is sandwiched between two fluid-heating plates, thus enabling temperature control.²⁰ Figure 1 also shows the experimental set up with AFR-LF modules and their connections used in this study.

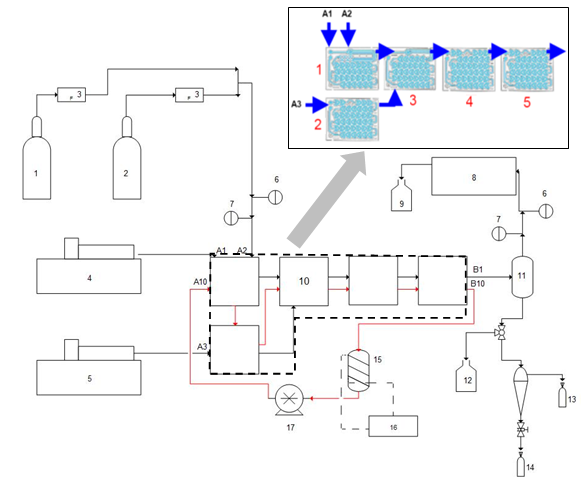
Figure 1 Schematic diagram of experimental setup for the Bunsen reaction using AFR-LF: (1) N₂ tank; (2) SO₂ tank; (3) Mass flow controller; (4) Organic syringe pump; (5) Water syringe pump; (6) Pressure indicator; (7) Temperature indicator; (8) Gas Chromatograph; (9) Scrubber; (10) Corning AFR-LF; (11) Gas-liquid separator; (12) Waste tank; (13) Organic phase sampling vial (14) Water phase sampling vial; (15) water (oil) bath (16) Temperature controller; (17) Hot fluid pump.

The internal volume of each fluidic module of the AFR-LF is about 0.4mL, which allows for liquid flow rates in the range of 0–10mL min^-1. Fluidic modules may be used in parallel or series, depending on the research requirements. At the beginning, five modules were used in series: Module 1 had two fluid inlet ports (A₁ and A₂), allowing two fluids to mix and/or react. Module 2 had one inlet port (A₃), allowing a third fluid to be introduced and conditioned to the same temperature. For experiments at room temperature, this module seemed useless. Modules 4 and 5 (when necessary) were used to extend the residence time. In later runs, one module was used for SO₂ absorption to reduce residence time. For a typical run, a gas mixture of SO₂ and N₂, supplied from cylinders and controlled by two mass flow controllers (1179A Mass-Flo^®, MKS), was fed to port A₂. Water and toluene were also pumped into the AFR-LF via ports A₁ and A₃ or A₃ and A₁, using 100-Legato KD scientific syringe pumps (Figure 1).

The experiments with AFR-LF were carried out at room temperature (22–25^°C), at different gas flow rates ranging from 53.6 to 85.7mL min^-1 at standard temperature and pressure (STP) and at different liquid flow rates (water from 0.3 to 0.7mL min^-1 and toluene from 0.65 to 1.3mL min^-1). The outlet of the AFR-LF was open to the atmosphere. A manual control valve was designed to keep the level of the liquid constant at the lower-middle of the separator so that the outlet gas can be easily purged only from the top of the separator to an online GC for analysis. At the bottom of the separator, liquid was collected in a separatory funnel where the organic phase was sampled using a glass Pasteur pipet and the water phase was sampled from the bottom. The experiment setup with AFR-G1 was similar to what Figure 1 shows, except that the gas samples were collected by using Cole-Parmer Tedlar bags at specific time intervals and analyzed by using an off-line instrument. The internal volume of each fluidic module of the AFR-G1 is about 20times that of the AFR-LF, i.e., 8mL, with a maximum allowable liquid flow rate of 200mL min^-1. The rest of the conditions, such as material, geometry, and design conditions, remained unchanged.

For this study two fluidic modules (modules 1 and 3) were usually used. Module 1 was used for mixing of two feeds, usually SO₂-N₂ and the organic phase, and module 3 was used for introducing water and mixing. As in the runs by using the AFR-LF, the gas mixture of SO₂ and N₂, from cylinders controlled by two mass flow controllers (5850S Smart Mass low, Brooks Instruments Inc.). Toluene and water were also pumped into the AFR-G1 by using a PTFE pump (Fuji Technic Tokyo) and a stainless steel pump (Jiangsu Hanbon Science & Technology Co.), respectively. The experiments were carried out at room temperature (22–25^°C), at different gas flow rates ranging from 1600 to 2000mL min^-1 at standard temperature and pressure (STP), and at different liquid flow rates (water from 30 to 60mL min^-1 and toluene from 37 to 79mL min^-1). The outlet of the AFR-G1 was also open to atmospheric pressure. Two 10L bottles of concentrated sodium hydroxide (5mol L^-1) were used in series to capture non-reacted SO₂ at the outlet of AFR-G1.

2. Chemicals

Chemicals used for the experiments with the AFR-LF were mostly ACS grade as received: sulfur dioxide (99.98%, Praxair), nitrogen (99.99%, Praxair), sodium hydroxide (97%, EMD), toluene (99.95%, BDH), and phenolphthalein and thyodene as the indicators. Chemicals were used as received without any modification or further steps of purification for the experiments with the AFR-G1 as well: sulfur dioxide (99.99%, Shanghai Weichuang Gas), nitrogen (99.999%, Changzhou Wujin Huayang Gas), sodium hydroxide (96%, Sinopharm Chemical Reagent), toluene (99.5%, Sinopharm Chemical Reagent), and phenolphthalein and thyodene were used as indicators. All the solutions used in both series of experiments and analyses were prepared by diluting the corresponding chemicals with deionized water.

3. Measurement techniques and analysis methods

For the experiments conducted using the AFR-LF, unreacted SO₂ was analyzed using a Varian CP-3800 gas chromatograph equipped with a thermal conductivity detector (TCD) after reaching steady state, roughly when the equivalent of three times the internal volume of the AFR-LF (or AFR-G1 in later experiments) had been processed. The internal normalization method was used for the gas calibration because this technique corrects for the sample-size error.²¹ However, for the experiments conducted using the AFR-G1, the external calibration method was used. Due to unavailability of the online method, gaseous sulfur dioxide samples were collected in Cole-Parmer Tedlar bags and were then analyzed using a Taizhou Zhonghuan Analysis Instrument Co. RPP-2000S Fluorescence Sulfur instrument at Changzhou University. Because the N₂ flow rate remains unchanged during absorption or reaction, the SO₂ flow rate in gas after absorption can be determined once its concentration in gas stream is known. The SO₂ absorption rate with respect to SO₂ can then be determined from the difference between the inlet and outlet SO₂ flow rates.

1. Liquid-side volumetric mass transfer coefficient by applying two-film theory in AFR

The two-film theory of mass transfer was used to determine the mass transfer coefficients of SO₂ across the gas/water and gas/toluene interfaces. According to this theory,²² the flux of the mass transfer of gas molecules A (SO₂ in this case) into liquid through the interface (z=0) can be written as:

${\text{N}}_{}=\frac{{\text{P}}_{}-{\text{H}}_{}{\text{C}}_{}}{\frac{1}{{\text{k}}_{}}-\frac{{\text{H}}_{}}{{\text{k}}_{}}}={\text{K}}_{}\left({\text{P}}_{}-{\text{P}}_{}^{\text{'}}\right)\text{ or }=\frac{\frac{{\text{P}}_{}}{{\text{H}}_{}}-{\text{C}}_{}}{\frac{1}{{\text{k}}_{}{\text{H}}_{}}-\frac{1}{{\text{k}}_{}}}={\text{K}}_{}\left({\text{C}}_{}^{\text{'}}-{\text{C}}_{}\right)$ (6)

Where N_A is the molar flux of A molecules from gas to liquid in the direction perpendicular to the mass transfer interface (mol∙m^-2s^-1), P_A is the partial pressure of A in gas phase (Pa), H_A is Henry’s law constant (Pa m³mol^-1), C_A is the concentration of A in liquid (mol m^-3), k_G is the mass transfer coefficient in the gas phase (mol m^-2s^-1Pa^-1) and k_L is the mass transfer coefficient in the liquid phase (m s^-1); ${\text{P}}_{\text{A}}^{\text{'}}$ = H_AC_A, and ${\text{P}}_{\text{A}}^{\text{'}}$ = P_A/H_A, K_G (mol Pa^-1m^-2s^-1) is the liquid-side volumetric mass transfer coefficient based on partial pressure driving force and K_L (ms^-1) is the liquid-side volumetric mass transfer coefficient based on liquid driving force. As explained later, the ideal plug-flow is assumed for liquid and gas through the fluid channels of both the LF and G1, and the performance equation is developed by combing the rate equation with the material (mole) balance. Taking a slice of the reactor along the material flow direction as the volume element (dV) for mass balance, of which the interface area per volume is a (m²m^-3, or m^-1),

$\text{A lost in gas phase}=-{\text{F}}_{\text{G}}{\text{dy}}_{\text{A}}=\text{A gained in liquid}=\frac{{\text{F}}_{\text{L}}}{{\text{C}}_{\text{t}}}{\text{dC}}_{\text{A}}={\text{ N}}_{\text{A},\text{ z}=0}\text{adV }$ (7)

Where, F_G and F_L are the total molar flow rates of gas and liquid (mol∙s^-1), respectively, and C_t is the total concentration of liquid (mol m^‑3). Considering y_A = P_A/P_t (P_t is the total pressure of gas), and combining Eqs (6) and (7), integration on either side gives the reactor volume (V_r).

${\text{V}}_{\text{r}}=\frac{{\text{F}}_{\text{G}}}{{\text{K}}_{\text{G}}\text{a}.{\text{P}}_{\text{t}}}\underset{{\text{P}}_{\text{A}1}}{\overset{{\text{P}}_{\text{A}2}}{{\displaystyle \int }}}\frac{{\text{dP}}_{\text{A}}}{\left({\text{P}}_{\text{A}}-{\text{P}}_{\text{A}}^{\text{'}}\right)}=\frac{{\text{F}}_{\text{L}}}{{\text{K}}_{\text{L}}\text{a}.{\text{C}}_{\text{t}}}\underset{{\text{C}}_{\text{A}1}}{\overset{{\text{C}}_{\text{A}2}}{{\displaystyle \int }}}\frac{{\text{dC}}_{\text{A}}}{\left({\text{C}}_{\text{A}}^{\text{'}}-{\text{C}}_{\text{A}}\right)}$ (8)

Upon integration of the liquid-side equation from inlet (C_A1) to outlet (C_A2), the liquid-side volumetric mass transfer coefficient (K_La) becomes

${\text{K}}_{\text{L}}\text{a}=\frac{1}{\text{τ}}\text{ln}\frac{{\text{C}}_{\text{A}}^{\text{*}}-{\text{C}}_{\text{A}1}}{{\text{C}}_{\text{A}}^{\text{*}}-{\text{C}}_{\text{A}2}}=\frac{1}{\tau }\text{lnX}$ (9)

Where,${\text{C}}_{\text{A}}^{\text{*}}$ is the equilibrium concentration of SO₂ in liquid phases (water or toluene) corresponding to the partial pressure of SO₂ in the gas phase at the inlet (P_SO2 in), C_A1 is the concentration of SO₂ in the liquid phase at the inlet, which is always zero, $\text{τ}$ is the residence time of the liquid flow in the AFR (V_rC_t/F_L), and ${\text{K}}_L\text{a}$ is the liquid-side volumetric mass transfer coefficient. ${\text{C}}_{\text{A}1}^{\text{*}}$ is calculated based on the partial pressure of SO₂ at the AFR inlet using Henry’s law;${\text{C}}_{\text{A}2}^{\text{*}}$ is obtained at the AFR outlets based on the dissolved SO₂ (the difference between SO₂ inlet and outlet in the gas phase and the liquid flow). Considering the residence time of the liquid, the liquid-side volumetric mass transfer coefficients in the LF and G1 at different operating conditions are estimated by Eq. (9). In fact, Eq. (9) has been used to calculate K_La in microscale and milliscale AFR, not only for gas-liquid adsorption systems but also for liquid-liquid absorption systems.²³ The volumetric mass transfer coefficient (K_La) is given because the liquid-side volumetric mass transfer coefficient based on liquid driving force, K_L, and the specific interface area, a, cannot be separated from each other and the determination of a is not within the scope of this study.

2. Flow regime analysis

The specific design of AFR is somewhat different from what is normally observed for straight channels. When the fluid enters the heart-shaped cell it hits the first curved post and splits into two streams until reaching a second cylindrical post where the two streams recombine.¹⁶ Therefore, for hydrodynamics study, the neck of the heart cell (H=400µm, W=300µm for the AFR-LF and H=1.12mm, W=1mm for the AFR-G1) is considered as the reference to define dimensionless parameters such as the Reynolds number.

$\text{Re}=\frac{{\text{ρuD}}_{\text{h}}}{\text{μ}}$ (10)

Where ρ and µ are the average density and viscosity of the fluids, respectively, u is the total superficial velocity of the two phases, and D_h is the hydraulic diameter. The diameter of the fluid channel at the connection of the two heart-shaped cells in an AFR is used for D_h. The density and viscosity of the fluids used are given in (Table 1).

Thus, for the AFR-LF, the gas and liquid flow rates range from 50 to 80 and 0.3 to 0.7mL min^-1, respectively, and the range of the two-phase Re is from 2360 to 3790, which is just above the critical value implying the transition to turbulent flow. For the AFR-G1, Re ranges from 12820 to 16320 for SO₂ and water flow rates within 800-1000 and 30-60mLmin^-1, respectively, indicating fully developed turbulent flow. The visualization experiments, which were done for a CO₂-water system by Nieves-Remacha et al.,¹⁶ using a AFR-G1, observed that two-phase flow in the AFR included a sequence of dynamic events: detachment, elongation, deformation, breakup, and coalescence of bubbles as they passed through the continuous phase. Confined geometry, small dimensions, and the presence of obstacles that disturb were mainly responsible for these events. Although these dynamic events were quite different from what had been observed in either stirred vessels or straight micro channels, tracer experiments for families of the AFR-LF and AFR-G1 showed the residence time distribution (RTD) to be narrow.²⁴ This indicates that each heart-shaped cell can be considered as an ideal stirred vessel in which complete mixing occurs. However, there must be no back mixing among cells and therefore, the flow throughout the whole AFR can be treated as plug flow.

3. The effect of changing feeding position of reactants

The AFR-LF was chosen to test the effect of mixing order of the gas mixture of N₂ and SO₂, water, and toluene, using the port combinations of A₁, A₂, and A₃, which allow mixing of any two fluids in the first module and mixing of the third in the second module. Along with the six possible combinations of mixing as well as the other experimental variables, the absorption rate results are given in Tables 2 and 3. Absorption runs at a gas flow rate of 85mL min^-1 at STP, SO₂ mole fractions (y_SO2=0.824), and two levels of water and toluene flow rates were conducted at room temperature. The results indicate that the SO₂ absorption rate by the liquid was independent of the feeding positions of the fluids. However, the slightly higher absorption rate in the latter Table was due to the higher toluene-to-water ratio. More toluene, which has the higher SO₂ solubility, would lead to a higher absorption rate. Although the same absorption rate can be achieved by either feeding sequence in the SO₂-water-toluene system, to maintain consistency in the experiments, the first and second feeding scenarios, i.e., mixing SO₂ with either liquid in the first module, were used for most of the runs in the subsequent experiments using both AFR-LF and AFR-G1 (Tables 2 and 3).

4. SO₂ absorption in water

Absorption in AFR-LF

Absorption runs with a constant gas flow rate (75mL min^-1 at STP) at various SO₂ mole fractions were conducted at room temperature and three water flow rates in the AFR-LF. (Table 4) details the experimental variables and calculated parameters from which the values of the overall mass transfer coefficients are obtained. Figure 2 shows the effects of SO₂ mole fraction and water flow rate on the SO₂ absorption rate and the liquid-side volumetric mass transfer coefficient, respectively.

A

B

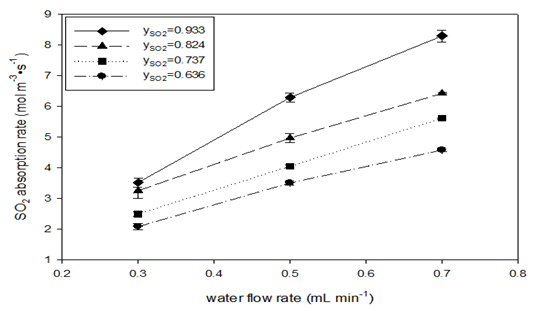
Figure 2 SO₂ absorption rate (A) and liquid-side volumetric mass transfer coefficient (B) vs. water flow rate in AFR-LF (Q_G = 75mL/min, T = 22-25^oC, ports: A₁, water and A₂, SO₂-N₂).

At a constant mole fraction of sulfur dioxide, a sharp increase could be seen in sulfur dioxide absorption rate when the flow rate of water was increased. Increase in the mole fraction of SO₂ at a constant water flow rate also increased the SO₂ absorption rate. The higher the water flow rate, the stronger the increasing effect of the mole fraction of SO₂ on its absorption rate. The same trend was observed as well when plotting the volumetric mass transfer coefficients vs. water flow rate for four levels of SO₂ mole fraction. At lower water flow rate, the effect of mole fraction is insignificant because the resistance to mass transfer is on the liquid side where the K_La value is low. At higher water flow rate, the resistance is shifted to the gas side to some extent and the gradient of SO₂ in gas phase begins to play a role. Nieves-Remacha et al. studied the effects of operating conditions on the hydrodynamics of a water-CO₂ system using a AFR-G1.¹⁶ They observed that the average bubble size and bubble size distribution depend on the gas and liquid flow rates. At the lower flow rate of water, most of the heart-shaped cells were occupied by large bubbles, which resulted in inadequate contact between the gas and liquid, and poor mass transfer across the interface. On the other hand, the bubble size decreased with increasing liquid flow (Q_L), which increased shear rates at the inlet of the heart-shaped cells. Greater turbulence in the water flow and increased specific area per volume of water resulted in larger K_La values.

Table 3 also shows that increasing the mole fraction of sulfur dioxide stabilized the equilibrium concentration of sulfur dioxide in the water at inlet ${\text{C}}_{\text{A}1}^{\text{*}}$ and ${\text{C}}_{\text{A}2}^{\text{*}}$ outlet, respectively, leading to an increase in volumetric mass transfer coefficients. Comparing the values of ${\text{C}}_{\text{A}2}^{\text{*}}$ and${\text{C}}_{\text{A}2}$ , two different behaviors were observed. At low mole fraction values of sulfur dioxide,  stayed below the equilibrium values, while at high mole fractions, the latter was higher. This was mainly due to the higher partial pressure of sulfur dioxide at the inlet that made SO₂ dissolve quickly in water. However, when the pressure at the outlet dropped significantly, a new equilibrium was hard to reach and the outlet concentration ${\text{C}}_{\text{A}2}$ became oversaturated (Table 4 & Figure 2).

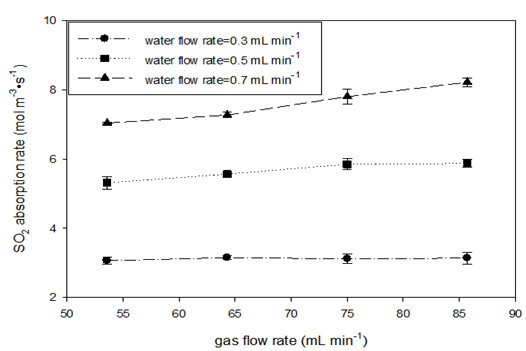
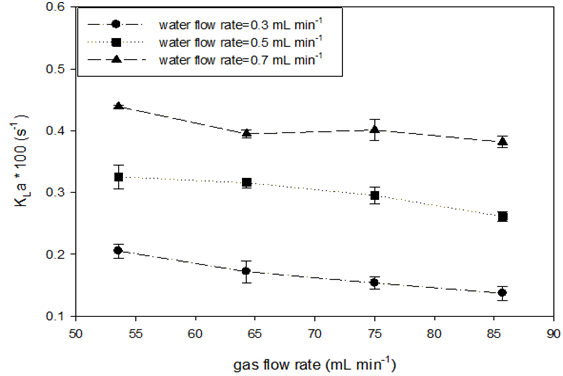
Absorption rates for a high mole fraction of gas (y_SO2=0.933) at various gas flow rates (at STP) were also measured at room temperature and three water flow rate levels. A high mole fraction was used to try to minimize the effect on the gas side. Table 5 shows the experimental variables and calculated parameters from which the values of mass transfer coefficients are obtained. (Figure 3) depicts the effects of gas flow rate and water flow rate on the SO₂ absorption rate and the volumetric liquid-side mass transfer coefficient. At two lower water flow rates, no significant changes in SO₂ absorption rate were observed when the gas flow rate was increased, as shown in Figure 3 (A). At the highest water flow rate, a small increase in absorption rate by gas flow was observed. The absorption capacity is determined by liquid flow once sufficient SO₂ is provided. However, the liquid-side volumetric mass transfer coefficients tended to decrease with increasing gas flow rate as shown in Figure 3 (B).

A

B

Figure 3 SO₂ absorption rate (A) and liquid-side volumetric mass transfer coefficient (B) vs. gas flow rate in AFR-LF (y_SO2 = 0.933, T = 22-25^oC, ports: A₁, water and A₂, SO₂-N₂).

This confirms the argument that increasing the gas flow rate increases the average bubble size, which in turn reduces the specific interface area.¹⁶ On the other hand, the absorption capacity was reached, resulting in quite similar outlet SO₂ concentrations in water ${\text{C}}_{\text{A}2}$ for each level of water flow rate. Because of the resistance to flow, the increase in gas flow led to total pressure increase and thus the increase in ${\text{C}}_{\text{A}1}^{\text{*}}$ . As a result, the logarithmic term of Eq. (9) began to decrease and then the coefficients became smaller. Comparing the values of ${\text{C}}_{\text{A}2}^{\text{*}}$ to ${\text{C}}_{\text{A}2}$ , oversaturation was also observed for most of the runs for SO₂ absorption in water. The third reason for a decrease in K_La with gas flow rate increase could be the effect on real residence time. At higher gas flow rate, the residence time determined by water flow rate was obviously longer than the real residence time. Then, the calculated K_La became smaller than it should be (Table 5 & Figure 3).

Absorption in AFR-G1

Absorption runs with a constant mole fraction of gas (y_SO2=0.50) at various gas flow rates at STP were conducted at room temperature and four water flow rate levels in the AFR-G1. (Table 6) provides the detailed experimental variables and calculated results. Figure 4 shows the effects of SO₂ flow rate and water flow rate on the SO₂ absorption rate and the volumetric liquid-side mass transfer coefficient, respectively.

A

B

Figure 4 SO₂ absorption rate (A) and liquid-side volumetric mass transfer coefficient (B) vs. water flow rate in AFR-G1 (y_SO2 = 0.50, T = 22-25^oC, ports: A₁, water and A₂, SO₂-N₂).

At a constant gas flow rate, a gradual increase in sulfur dioxide absorption could be seen when the water flow rate was increased. At a constant water flow rate, the absorption rate of sulfur dioxide was also increased steadily by increasing the gas flow rate. On the other hand, the volumetric mass transfer coefficient values were relatively stable with the change of the water flow rate at 1600mL min^-1 of the gas flow rate. While the data of K_La vs. water flow at 1800 and 2000mL min^-1 gas flow rates overlapped at larger values, they tended to decline marginally with the increase in water flow rates. This observation differs from the findings in the AFR-LF as well as the result from the study of the CO₂-water system by Nieves-Remacha et al.¹⁶ As can be seen from (Table 6), at a constant gas flow rate, the value of C_A2 was reduced by increasing the flow rates of water, while  was increased, the larger gap between the two concentrations resulted in smaller values of the second term of Eq. (11). On the other hand, the residence time was reduced, which in turn resulted in an increase of 1/τ values. At these critical conditions, the effect of shortening the residence time and the change of SO₂ concentrations by gas and water flow rates balanced, leading to relatively stable volumetric mass transfer coefficients. While the shortening of residence time by increasing the water flow tipped the scales, a decrease of the coefficients was observed. At constant values of water flow, the increase of gas flow from 1600 to 1800mL min^-1 led to a relatively small increase in K_La; however further increase in gas flow rate resulted in no further change in K_La. This may indicate that the mass transfer in absorption was not controlled by the SO₂ transportation on the gas side (Table 6 & Figure 4).

5. SO₂ absorption in toluene

Absorption in AFR-LF

In runs similar to those using water as solvent for SO₂ absorption, the solvent was switched toluene and the absorption was first run with a given gas flow rate (75mL/min at STP) at four levels of SO₂ mole fraction (0.636–0.933), three toluene flow rate levels (0.65–12.7mL min^-1), and at room temperature. (Table 7) details the experimental variables and the calculated results.

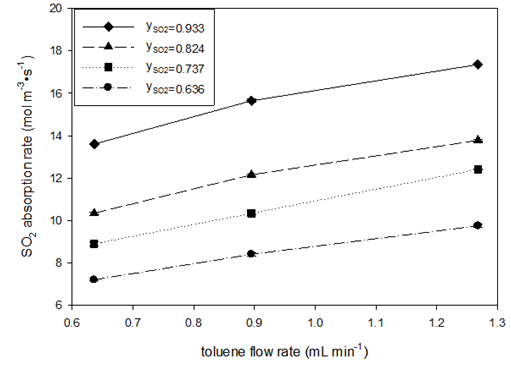
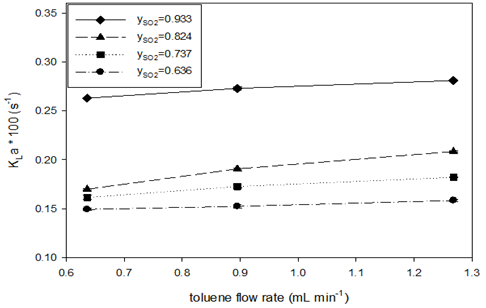
Compared to (Table 4), the flow rate range of toluene was two times that of water. This is roughly determined by the stoichiometry of the Bunsen reaction, the solubility of iodine in toluene and water, and the excessive use of water. (When multiphase absorption and the Bunsen reaction (part two) are carried out with iodine-toluene solution, the flow rate of toluene used can be 2 to 4 times that of water.) This also means that, relative to the same levels of SO₂ flow rate, higher flow rate of toluene was used than that of water. Table 7 also shows that the values of the outlet equilibrium concentrations ${\text{C}}_{\text{A}2}^{\text{*}}$ are always larger than the outlet concentration ${\text{C}}_{\text{A}2}$ of SO₂ in toluene, indicating that absorption equilibrium has not been achieved in toluene absorption. Unlike in water absorption, no oversaturated absorption was observed for toluene. (Figure 5) depicts the effects of SO₂ mole fraction and toluene flow rate on the SO₂ absorption rate and the volumetric liquid-side mass transfer coefficient.

A

B

Figure 5 SO₂ absorption rate (A) and liquid-side volumetric mass transfer coefficient (B) vs. toluene flow rate in AFR-LF (Q_G = 75mL/min, T = 22-25^oC, ports: A₁, toluene and A₂, SO₂-N₂).

The absorption rate was reduced by increasing SO₂ mole fractions and toluene flow rates, which can be explained by the increase in absorption driving force. The higher values of K_La at higher mole fraction of SO₂ may imply resistance to mass transfer on the gas side, and the increasing K_La values at higher toluene flow rate means greater interface areas between gas and liquid for a unit volume of liquid. Comparing the effects of water and toluene flow rate on SO₂ absorption, it was found that the increase of absorption rate and the volumetric mass transfer coefficient with water flow rate is sharper than that with toluene flow rate. At a similar liquid flow rate (water at 0.7mL min^-1 and toluene at 0.65mL min^-1) with the range of SO₂ mole fraction in gas phase (0.646–0.933), toluene showed higher absorption rates (7–13.5mol m^-3s^-1) than water (4.2–8.4mol m^-3s^-1); however, water had higher values of the volumetric mass transfer coefficient (0.0028–0.0047s^-1) than toluene (0.0015–0.0026s^-1). The higher absorption rate in toluene can also be attributed to differences in the driving force of mass transfer. The solubility of SO₂ in toluene is more than 10 times its solubility in water. With the same partial pressure of SO₂ in gas, the mass transfer driving force, , would be 10 times that in toluene initially when C_A is zero. The lower K_La for toluene may be because the specific interface area in toluene is smaller than in water and the diffusivity of SO₂ is smaller in toluene than in water.

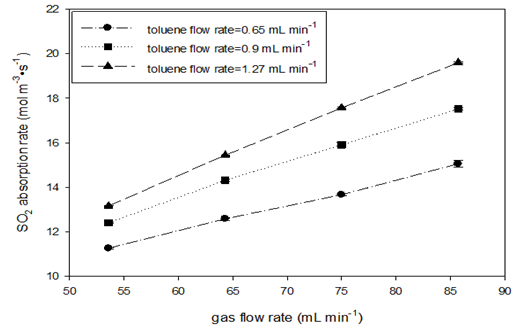
(Table 7 & Figure 5) Absorption rates at various gas flow rates (at STP) with a high mole fraction of SO₂ (y_SO2=0.933) were also measured at room temperature and three toluene flow rate levels. High SO₂ mole fraction was used to minimize gas-side mass transfer resistance. (Table 8) gives the detailed experimental variables and calculated results. Figure 6 shows the effects of gas flow rate on the SO₂ absorption rate and the volumetric liquid-side mass transfer coefficient. At a constant toluene flow rate, SO₂ absorption rate and mass transfer coefficients were sharply increased with gas flow rates. This behavior is different from what has been observed in SO₂-water systems where the absorption rate seemed to be independent of the gas flow rate and the K_La value decreased with increasing gas flow. However, this observation is in agreement with Nieves-Remacha et al.,¹⁶ where increase in flow rate of each gas and liquid phase has a positive effect on the volumetric mass transfer coefficient of CO₂ into water. It is believed that the increase in K_La with increasing gas flow is due to the increase in specific interfacial area (Table 8 & Figure 6).

A

B

Figure 6 SO₂ absorption rate (A) and liquid-side volumetric mass transfer coefficient (B) vs. gas flow rate in AFR-LF (y_SO2 = 0.933, T = 22-25^oC, ports: A₁, toluene and A₂, SO₂-N₂).

Absorption in AFR-G1

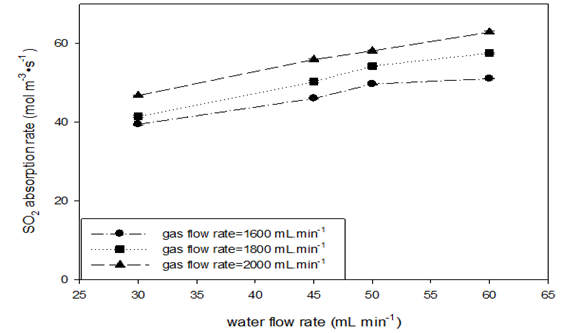
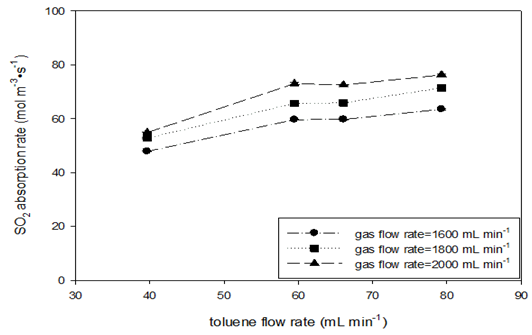
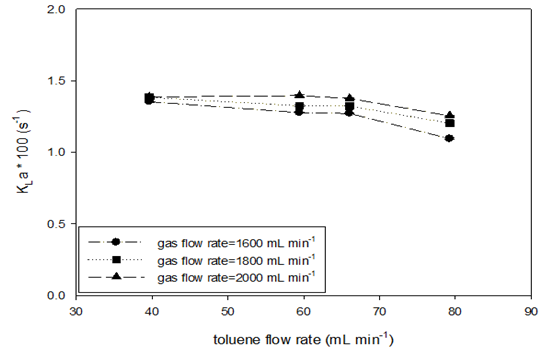
Absorption runs with a constant gas mole fraction (y_SO2=0.50) at various SO₂ flow rates at STP were conducted at room temperature and four toluene flow rate levels. Table 9 shows the experiment variables and calculated results. Figure 7 shows the effects of increasing gas and toluene flow rates on the SO₂ absorption rate and the liquid-side volumetric mass transfer coefficient. Increasing the toluene flow rate led to an increase in the absorption rate values in the beginning (Figure 7 (A)); however, the data became constant at the higher flow rate of toluene. At each level of toluene flow rate, the effect of increasing gas flow on the absorption rate appeared more obvious, similar to what was observed using the AFR-LF. In (Figure 7 (B)), the K_La values seem to be insensitive to both toluene and gas flow rates, which is similar to the observation for the AFR-LF. Increasing the toluene flow rate by a factor of two maintained the K_La values at the same margin (0.011–0.014s^-1). At lower toluene flow, the K_La value change by gas flow increasing from 1600 to 2000mL min^-1 (40% increase) is negligible (<3 %) Even at higher toluene flow, this change is still small (<15 %). However, the K_La value obtained in the AFR-G1 is 4-6 times that obtained in the AFR-LF (Table 9 & Figure 7).

A

B

Figure 7 SO₂ absorption rate (A) and liquid-side volumetric mass transfer coefficient (B) vs. toluene flow rate in AFR-G1 (y_SO2 = 0.50, T = 22-25^oC, ports: A₁, toluene and A₂, SO₂-N₂).

6. SO₂ absorption in water-toluene mixture

Absorption in AFR-LF

Absorption runs with a constant mole fraction of SO₂ (y_SO2 =0.933) and liquid flow rate (1.5mL min^-1) at various gas flow rates at STP were conducted at room temperature (22–25^oC) for SO₂ in water-toluene mixture where the gas phase resistance was negligible. The purpose of this experiment was to understand the effects of increasing water volumetric fraction in water-toluene and SO₂ flow rate in SO₂-N₂ mixtures in the described system as shown in Figure 8 (A). By definition water volumetric fraction equals water flow rate divided by total liquid flow rate. As can be seen, at a constant water fraction, a sharp increase could be seen in sulfur dioxide absorption rate when the flow rate of SO₂ was increased from 53.57 to 85.72mL min^-1. The lower the water fraction, the stronger the increasing effect of the SO₂ flow rate on its absorption rate. On the other hand, an increase in water fraction at a constant gas flow rate decreased the SO₂ absorption rate. This decreasing trend was less tangible at lower water fraction rate when mixture was mainly consisted of toluene. The absorption runs were repeated at room temperature with constant mole fraction of gas (y_SO2=0.933) and constant water volumetric fraction at various gas flow rates at STP and five liquid flow rate levels as shown in Figure 8 (B).

A

B

Figure 8 (A) SO₂ absorption rate vs. water volumetric fraction in AFR-LF and (B) SO₂ absorption rate versus liquid flow rate in the AFR-LF (liquid flow rate=1.5 mL/min for Fig.8 (A), water volumetric fraction=0.25 for Fig.8 (B), mole fraction of SO₂=0.933, T=22-25^oC, ports A₁, toluene, A₂, SO₂-N₂ and A₃, Water).

Clearly, at all gas levels, enhancing liquid flow rates increased the absorption rates. However, larger liquid flow rates gave a smoother rise to absorption values mainly due to the fact that complete absorption of SO₂ in toluene was more likely achieved at larger liquid flow rates. Similar to (Figure 8 (B)), absorption rates of SO₂ were increased at a constant liquid flow rate by increasing gas flow rates, leading to an increase in mass transfer at high flow rates. The observation in section 3.6 confirms the argument in previous sections where the higher absorption rate in toluene was attributed to differences in the driving force of mass transfer due to higher solubility of SO₂ in toluene than in water. In the following section, similar experiments were conducted for the ternary SO₂-water-toluene system in AFR-G1 at a constant water volumetric fraction.

Absorption in AFR-G1

The absorption runs with a constant mole fraction of gas (y_SO2=0.50) and water volumetric fraction (0.15) at various gas flow rates at STP were conducted at room temperature (22–25^oC) and four liquid flow rate levels. Figure 9 shows the effects of the liquid flow rate and gas flow rate on the SO₂ absorption rate. Increasing the liquid flow rates smoothly increased the absorption rates. An increase in gas flow rates also increased the absorption rates of SO₂ at a constant liquid flow rate which is fairly similar to what was observed in AFR-LF (Figure 9).

Figure 9 SO₂ absorption rate versus liquid flow rate in the AFR-G1 (mole fraction of SO₂=0.50, water volumetric fraction =0.15, T=22-25^oC, ports A₁, SO₂-N₂, A₂, toluene and A₃, Water).

Scalability study of SO₂ absorption in LF and G1

The foregoing discussion is not definitive concerning the scalability of the two levels of AFR’s. Specifically, the results showing the effect of water flow rate on K_La from the AFR-LF is not in agreement with that from the AFR-G1. The K_La values of the SO₂-water and SO₂-toluene absorption for both AFR are not in the same order of magnitude either. Experiments using different numbers of modules of AFR-LF (one vs. five) for two systems (SO₂-water and SO₂-toluene) resulted in the same magnitude of overall absorption rate and a different order of magnitude for K_La (Tables 10).

The values of K_La from one module are about 6–7 times those from five modules. This indicates that the absorption has been completed in one module and that the remaining modules contribute negligibly to the absorption, which merely extends the residence time and results in smaller K_La from the AFR-LF as in previous sections. Therefore, absorption runs were conducted using one single-module AFR-LF, as described in this section. Then, the new SO₂ absorption results of the one single module AFR-LF are compared with the results of the SO₂ absorption runs using the AFR-G1, where a single module was used. K.F. Jensen’s group at MIT studied the scalability of these two scales of AFR for liquid-liquid mass transfer.²³ The method that was used was to plot the K_La values vs. the residence time for both AFR. By analyzing the magnitude of the K_La and the curves of K_La vs. residence time, the scalability across these two sizes of the AFR is evaluated. (Figure 10) plots the K_La of SO₂ absorption in water and toluene using one-module LF and G1 vs. residence time.

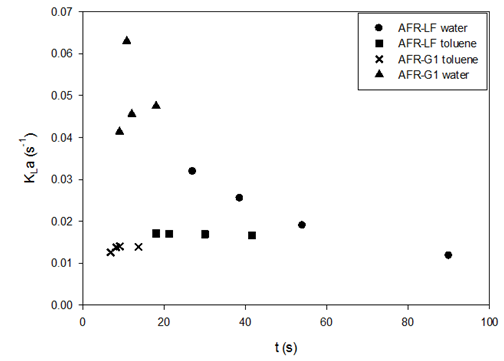
Figure 10 Liquid-side volumetric mass transfer coefficients vs. liquid residence time (t) in AFRs for SO2 absorption in water and toluene at room temperature.

Due to the significant differences in channel sizes and heart-shape cell layout, the smooth change of the K_La vs. residence time across the two levels of ARFs and the relatively similar magnitudes of volumetric mass transfer coefficients indicate seamless scalability of the AFR. The shape of K_La vs. residence time for SO₂-water is the same as that for the liquid-liquid system in;²³ however, the shape for the SO₂-toluene system is different. The changes in polarity, viscosity, and surface tension of the solvent may change the mass transfer behavior for a given gas in the same AFR (Figure 10).

To study low-temperature Bunsen reaction using iodine-toluene solution in the H₂S splitting cycle for hydrogen production, the absorption behavior of SO₂ in water and toluene was studied in the absence of iodine and the scalability of mass transfer across both micro-and milli-scales of the AFR modules was evaluated. The following conclusions can be drawn from this study:

1. For both SO₂-water and SO₂-toluene absorption systems, varying the mole fraction of SO₂ in gas phase indicates that the gas-side mass transfer resistance is significant.
2. For an SO₂-water system using the AFR-LF, increasing the liquid flow rate at a fixed gas flow rate results in an increase in SO₂ absorption rate and the liquid-side volumetric mass transfer coefficient. However, increasing the gas flow rate at a fixed liquid flow rate results in only insignificant change in SO₂ absorption rate and a slight drop in the liquid-side volumetric mass transfer coefficient. Using the AFR-G1, increasing both gas and liquid flow shows insignificant effect on both absorption rate and liquid-side volumetric mass transfer coefficient.
3. For SO₂-toluene system using the AFR-LF at a fixed liquid flow rate, increasing gas flow rate results in an increase in SO₂ absorption rate and the liquid-side volumetric mass transfer coefficient. However, at a fixed gas flow rate, the increase in liquid flow rate just leads to an increase in absorption rate and insignificant change in the liquid-side volumetric mass transfer coefficient. Using the AFR-G1, the increase in the gas and liquid flow rates leads to an increase in absorption rate and insignificant change in the liquid-side volumetric mass transfer coefficient. Even at lower gas flow rates, increasing liquid flow rate leads to a decrease in the mass transfer coefficient.
4. For SO₂-water-toluene system, SO₂ had higher solubility in toluene than water due to differences in the driving force for mass transfer in both AFR-LF and AFR-G1.
5. The magnitude of the liquid-side volumetric mass transfer coefficient and its change with residence time indicate straightforward and seamless scalability across both the LF- and G1 scales of the AFR.

Greek letters

τ                               Residence time, s

None.

The author declares that there are no conflicts of interest.

1. Laureshen CJ. From oil sand bitumen to petrochemical feedstock. Oil and Gas Processing Review. 2006.
2. Wang H. Hydrogen production from a chemical cycle of H2S splitting. Inter J of Hydrogen Energy. 2007;32(16):3907‒3914.
3. Brown LC, Besenbruch G, Lentsch R, et al. Alternative flowsheets for the sulfur‒iodine thermochemical hydrogen cycle: United States. Department of Energy. Oakland Operations Office. 2003.
4. Funk JE. Thermochemical hydrogen production: past and present. Inter J of Hydrogen Energy. 2001;26(3):185‒190.
5. Giaconia A, Caputo G, Ceroli A, et al. Experimental study of two phase separation in the Bunsen section of the sulfur–iodine thermochemical cycle. Inter J of Hydrogen Energy. 2007;32(5):531‒536.
6. Norman JH, Besenbruch GE, O’Keefe DR. Thermochemical Water‒Splitting for Hydrogen Production, GRI‒80/0105. Gas Research Institute. 1981.
7. Sakurai M, Nakajima H, Onuki K, et al. Investigation of 2 liquid phase separation characteristics on the iodine–sulfur thermochemical hydrogen production process. Inter J of Hydrogen Energy. 2000;25(7):605‒611.
8. Sakurai M, Nakajima H, Amir R, et al. Experimental study on side‒reaction occurrence condition in the iodine–sulfur thermochemical hydrogen production process. International Journal of Hydrogen Energy. 2000;25(7):613‒619.
9. De Beni G, Pierini G, Spelta B. The reaction of sulphur dioxide with water and a halogen. The case of iodine: reaction in presence of organic solvents. International Journal of Hydrogen Energy. 1980;5(2):141‒149.
10. Nomura M, Fujiwara S, Ikenoya K, et al. Application of an electrochemical membrane reactor to the thermochemical water splitting IS process for hydrogen production. Journal of Membrane Science. 2004;240(1‒2):221‒226.
11. Nomura M, Nakao S-i, Okuda H, et al. Development of an electrochemical cell for efficient hydrogen production through the IS process. AIChE Journal. 2004;50(8):1991‒1998.
12. Sau S, Giaconia A, Caputo G, et al. Decrease the rate of recycling agents in the sulfur–iodine cycle by solid phase separation. International Journal of Hydrogen Energy. 2008;33(22):6439‒6444.
13. Wang H, Le Person A, Zhao X, et al. A low-temperature hydrogen production process based on H2S splitting cycle for sustainable oil sands bitumen upgrading. Fuel Processing Technology. 2013;108:55‒62.
14. Fan Y, Herz RK. Measurement and enhancement of gas-liquid mass transfer in milliliter-scale slurry reactors. Chemical Engineering Science. 2007;62(21):5940‒5951.
15. Li J, Moniri A, Wang H. Apparent kinetics of a gas–liquid–liquid system of Bunsen reaction with iodine-toluene solution for hydrogen production through H2S splitting cycle. International Journal of Hydrogen Energy. 2015;40(7):2912‒2920.
16. Nieves Remacha MJ, Kulkarni AA, Jensen KF. Gas-Liquid Flow and Mass Transfer in an Advanced Flow Reactor. Industrial & Engineering Chemistry Research. 2013;52(26):8996‒9010.
17. Lavric ED, Woehl P. Advanced‒FlowTM glass reactors for seamless scaleup. Chemistry Today. 2009;27:45‒48.
18. Chivilikhinl MS, Kuandykovl L, Lavric ED, et al. Residence Time Distribution in Corning® Advanced-FlowTM Reactors. Experiment and Modelling. Chemical Engineering Transactions. 2011;25:791‒796.
19. Lavric ED. Thermal performance of Corning glass microstructures. Proceedings of the Heat Transfer and Fluid Flow in Microscale III Conference. 2008.
20. Braune S, Pöchlauer P, Reintjens R, et al. Selective nitration in a microreactor for pharmaceutical production under CGMP conditions. Chemistry Today. 2009;27:26‒29.
21. Grob RL, Barry EF. Modern practice of gas chromatography, 4th ed. 2004.
22. Levenspiel O. Chemical reaction engineering. Industrial & Engineering Chemistry Research. 1999;38:4140‒3.
23. Woitalka A, Kuhn S, Jensen KF. Scalability of mass transfer in liquid–liquid flow. Chemical Engineering Science. 2014;116:1‒8.
24. Chivilikhinl MS, Kuandykovl L, Lavric ED, et al. Residence Time Distribution in Corning® Advanced‒FlowTM Reactors. Experiment and Modelling. Chemical Engineering Transactions. 2011;25:791‒796.