International Journal of
eISSN: 2475-5559


Research Article Volume 3 Issue 4
1Department of Chemical Engineering, Ferdowsi University of Mashhad, Iran
2Department of Chemical Engineering, Mazandaran University of Science and Technology, Iran
Correspondence: Mehrzad Arjmandi, Department of Chemical Engineering, Faculty of Engineering, Ferdowsi University of Mashhad, Mashhad, Iran, Tel 98 9112108990
Received: March 08, 2018 | Published: September 10, 2018
Citation: Arjmandi M, Ahmadpour A, Arjmandi A. A new approach for determination of adsorption energy for each adsorption site and improve conventional adsorption isotherms. Int J Petrochem Sci Eng. 2018;3(5):131-142. DOI: 10.15406/ipcse.2018.03.00087
In the present study, a new approach for determination of energy distribution (ED) of heterogeneous solid adsorbents is presented. This approach implements pore size distribution (PSD) data of a porous adsorbent obtained from adsorption measurements to estimate the ED of the solid. Moreover, the proposed algorithm imposes some modifications on the conventional adsorption models to improve them and provide better prediction of adsorption behavior. Adsorption data of four different heterogeneous cases were used to evaluate the proposed algorithm. From the results, the proposed algorithm provided better estimation of adsorption isotherm than conventional adsorption models such as Unilan, Toth and Sips as well as easily calculated ED. The accuracy of the proposed algorithm is greatly depends on selection of appropriate PSD determination method. The proposed algorithm regarded as a trustworthy procedure for reliable estimation of ED of heterogeneous solid adsorbents.
Keywords: energy distribution, adsorption isotherme, Kelvin, SHN1, PSD
Adsorption is a surface phenomenon that one or more substances which are originally presented in a fluid phase would remove from that phase by accumulation at the interface between the fluid and a solid surface. Adsorption mechanisms are typically classified as physical, chemical and electrostatic adsorption, in which for the gas separation systems, the physical adsorption is only considered. In the case of physical adsorption, weak intermolecular forces such as van der Waals provide the required driving force of the process.1 Generally, physical adsorption data is used to describe the main characteristics of the solid surfaces.2,3 The adsorption that occurs on different sites of the solid surface follows the adsorption isotherms.4 The early presented models for prediction of gas adsorption on a solid surface assumed the surface to be uniform and homogeneous. The first quantitative model was discussed by Langmuir assuming monolayer coverage.6
Brunner, Emmett and Teller (BET) proposed an adsorption isotherm with multilayer adsorption on the solid surface.6 Both Langmuir and BET isotherms are based on kinetic mechanisms and assume adsorption occurring on fixed sites of the surface with no lateral interactions among adsorbed molecules. Such isotherms could be applied reliably for solids with uniform pores. However, porous media include pores with different sizes and this pore size distribution can severely affect the adsorption characteristics and surface area of the sorbent.7,8 Since pores with various sizes, have different energies, one of the greatest problems of physical adsorption is the precise description of the heterogeneity of the adsorbent. Many investigators working in the field of physical adsorption have devoted their researches to this problem,9 but the issue of heterogeneity is still one of the great unresolved problems in this field. Accurate estimation of energy distribution and/or pore size distribution of non homogeneous adsorption systems is considered as an important design and operational consideration.10 Adsorption measurement on each solid site with identified energy is an impractical process; as a result, relatively complex theories are applied in many cases for estimation of such distributions.11
There have been several researches regarding determination of energy distribution (ED) for heterogeneous adsorbents.12‒15 In 1987, Tarazona13 applied Density Functional Theory (DFT) to the adsorption isotherms. Merz14 used the regularization technique along with the generalized cross-validation (GCV) for estimation of ED using Langmuir and BET isotherms. House15 applied the second order penalized least square (PLS) for the prediction of ED in heterogeneous solid adsorbents. Duda16 investigated ED of microporous systems using multivariate identification. Various models have been proposed for estimation of pore size distribution (PSD)17‒27and ED14‒16,25,28‒32for solid adsorbents. However, by estimating an ED by one of these methods, the conventional isotherms with constant adsorption energy could not be reliably applied. In other words, by even applying an identified ED function, it is impossible to obtain related energy for all solid pores individually and adsorption measurement on such pores with different energies is impractical.
In this study, a new algorithm (called M.A.A algorithm) is presented for determination of ED of heterogeneous solid adsorbents. In this algorithm, the PSD of adsorbent is first determined by the method proposed by Shahsavand26, and then by considering some assumptions (that are discussed in the theory section) and following the presented algorithm, the ED would be determined. The advantage of the proposed algorithm is that by following such procedure it is possible to evaluate an energy related to solid pores and subsequently determine the amount adsorbed on each solid site with the identified energy. The success of this algorithm is greatly depends on choosing an accurate method for the estimation of PSD of solid adsorbent in addition to maximum and minimum of surface energy that is usually predetermined values or could be determined by doing a few and simple experiments.
Adsorption Isotherms
As mentioned before, adsorption occurs on the surface of a solid and follows the adsorption isotherms.4 A wide variety of equilibrium isotherm models such as Langmuir, Freundlich, BET, Redlich-Peterson, Dubinin-Radushkevich, Temkin, Toth, Koble-Corrigan, Sips, Khan, Hill, Flory-Huggins and Radke-Prausnitz have been proposed by many researchers based on three different approaches including kinetic, thermodynamic and potential.33 Based on the kinetic approach, adsorption equilibrium is defined a situation in which the adsorption and desorption rates are equal.5‒34 The thermodynamics provide framework for deriving numerous forms of adsorption isotherm models as the second approach.12‒35 The potential theory, as the third approach, usually conveys the main idea in the generation of characteristic curve.36
Generally, adsorption isotherms could be classified into three categories of two parametric isotherms (e.g. Langmuir, Freundlich, Dubinin–Radushkevich, Temkin, Flory-Huggin, Volmer and Hill), three parametric isotherms (e.g. Redlich–Peterson, Sips, Toth, Unilan, Koble–Corrigan, Khan, Radke-Prausnitz, Fowler-Guggenhein and Hill-deBoer), and multilayer adsorption (BET).4 In order to investigate improvement of conventional adsorption isotherms by using the proposed algorithm, three widely used isotherms of Sips, Toth and Unilan were evaluated among various adsorption isotherm models due to the it simplicity as well as having the desired accuracy.
Sips isotherm
The Sips isotherm is a combination of Freundlich and Langmuir models that is used for adsorption systems with heterogeneous surfaces. Unlike Freundlich isotherm37 that does not provide accurate estimation at high levels of pressure, the Sips model predicts accurate estimation even at high pressures. However, both models do not satisfy the Henry’s law38 at very low pressures. The Sips isotherm is described as:
Cμ=Cμs(bP)1n1+(bP)1n (1)
b=b∞exp(QRT) (2)
Where, P denotes the adsorption pressure, Cµ is the amount adsorbed, Cµs maximum amount adsorbed at adsorption temperature of T, and b is the adsorption affinity at infinite temperature and n is a constant parameter. As it seen from the above equations, the Sips model is similar to the Langmuir isotherm; however the only difference between them is addition of parameter ''n'' in the Sips model which is a measure of the heterogeneity nature of the adsorbent surface with n=1 for the homogeneous surfaces.1
Toth isotherm
Unlike Sips model that does not satisfy the low pressure limit, the Toth isotherm is capable of satisfying both high and low pressure limits as well as the Henry’s law.1,39 This equation describes well many systems with sub-monolayer coverage. The Toth isotherm is described by the following equation:
Cμ=Cμsbp[1+(bp)t]1/t (3)
b=b∞exp(QRT) (4)
Where t is a constant parameter
Unilan isotherm
The Unilan equation is another empirical relation that obtained by assuming a patch wise topography on the solid surface and each patch is ideal such that the local Langmuir isotherm is applicable over each patch. The Unilan equation provides well behaviors at low and high pressures. This isotherm is described as:
Cμ=cμs2sln(1+ˉb.exp(s)P1+ˉb.exp(−s)P) (5)
ˉb=b∞exp(ˉERT) (6)
ˉE=Emax+Emin2 (7)
s=Emax−Emin2RT (8)
Where Emax and Emin are maximum and minimum energies of distribution and b ̅ is the adsorption affinity at infinite temperature. The parameter ''s'' characterizes the heterogeneity of the system.
Physical adsorption on heterogeneous surfaces could be described by Fredholm integral equation. In general, the Fredholm integral equation of the first kind is characterized by the following definite integral:40‒42
g(t)=b∫aK(t,s)F(s)ds (9)
In which, F(s) is an unknown distribution function that should be determined and K(t,s) is kernel (isotherm) of the equation that would be chosen based on the adsorbent, adsorbates, pressure and temperature of an adsorption process. It is assumed that the adjacent adsorption sites do not have any energy interferences. It can described, with a good approximation, the relation between the amounts adsorbed on any sites of the solid with particular energy, adsorption pressure and temperature using the Langmuir equation. This integral equation could be safely applied for the determination of PSD and ED of an adsorbent as follows:
g(t)=b∫aK(t,s)F(s)ds (10)
g(Pi)=emax∫eming(e,Pi,T)F(e)de (11)
From this equation, it is clear that having the amount adsorbed on the adsorbent at constant temperature and different pressures as well as adsorption isotherm and integral limits; it can easily compute PSD and ED of the porous solid. However, calculation of ED in most cases is usually done by determining the most frequent energy within the adsorbent assuming this constant and uniform energy for the solid surface and considering the energy as a known parameter of the adsorption isotherm. This assumption has high accuracy for homogeneous adsorbents; but by increasing heterogeneity of the surfaces the accuracy is reduced. On this basis, the related energy of any adsorption pressure should be determined.
As a new approach for determination of ED of a solid adsorbent presented here, it is necessary to determine the PSD of the solid in advance. As it is shown in Eq. (4), constant parameter of total energy of solid is used for the calculation of affinity coefficient ''b''. Since all this parameters are fixed, the parameter ''b'' is considered constant. In reality, parameter ''b'' is not constant within the system and should be determined for each adsorption site. For calculating this parameter for each site on the solid, the related energy should be determined beforehand. With respect to Eq. (6), the maximum and minimum energy of adsorption could be determined experimentally and average of these values could be considered as adsorption energy in the Unilan equation. This procedure is applied for different isotherms. It should be noted that we aimed to determine corresponding adsorption energy for each adsorption site. In other words, at each pressure the energy of the adsorbent should be defined. On this basis, parameters Q, E and b in the isotherm models should not be considered constants and only function of adsorption pressure. The proposed procedure is shown in Figure 1.
In order to follow the procedure depicted in Figure 1, ED equation should be known. However, various conventional methods of computing ED could not follow the presented procedure. That is why we need to follow a different path where the required information is available. Here, we introduce an indirect path for computing Ei and bi at each operational pressure that is presented on Figure 2.
The proposed algorithm (M.A.A) with the priori assumptions are described below:
dr=limn→∞(|rmax−rmin|n) (12)
Do the same procedure to the step 4 for determination of de with respect to maximum and minimum energy of the solid.
de=limn→∞(|Emax−Emin|n) (13)
Using the following equation (Do 1998), the ED would be determined from the PSD function obtained in step 3.
f(e)=f(r).drde (14)
In this equation, it is assumed that energy in the pores depends only on the radius of the pore and other factors do not affect it. In other words, the shape of energy distribution function is similar to the PSD ones.The main goal is to relate energy of each pore to the adsorption pressure. In step 6, relationships between pressure and energy have presented and now must establish a relationship between the pore radius and pressure. Therefore, we should obtain a radius corresponds to the condensation or evaporation pressure using Kelvin equation.34
rk(Pi)=σcosθϑMRTln(PoPi) (15)
rk(Pi)=2σcosθϑMRTln(PoPi) (16)
Where, the threshold radius rk for both condensation and evaporation cases can be computed from the Kelvin equation, respectively. In these equations, σ denotes surface tension, νM molar volume of liquid and P0 vapor pressure of the bulk phase. Kelvin equation is the only model that provides a relation between pressure and pore radius which is used for N2 adsorption data.
The PSD of solids investigated in this study are determined by a linear regularization method43‒46 provided by Shahsavand27 They have provided an accurate and reliable method for correct estimation of PSD for the porous solids from nitrogen adsorption data using Eq. (11).
Four different cases were used to evaluate the proposed algorithm. Usually, studies of surface properties pore size, pore volume and chemical composition of the available surface is done using nitrogen adsorption at liquid N2 temperature of 77K.47 For this reason, N2 adsorption data of four different adsorbents were used to evaluate the proposed algorithm. The maximum energy of these adsorbents was obtained from the experimental data using regression method and they are presented in Table 1. Moreover, the PSD of each solid was determined using the first order linear regularization method. Using any other method to calculate PSD with sufficient accuracy is also allowed. In each case, three isotherms of Unilan, Sips and Toth are used with some modifications by the proposed algorithm and plotted to evaluate their improvement.
Case study 1
The adsorption data of Controlled pore glass (CPG-69) heterogeneous adsorbent was used as the first case study. CPG is produced from a special alkali-borosilicate material which is heated above the annealing point but below the temperature that would cause deformation. During this heat operation, two continuous closely intermingled glassy phases are produced. One phase is rich in alkali and boric oxide and is easily soluble in acids and another phase is rich in silica and is insoluble. The borate and alkali phase is washed out by acid solutions at high temperatures followed by a treatment with sodium hydroxide and by washing with water.48According to the proposed algorithm, the PSD of solid was determined using linear regularization method and a Gaussian function was fitted to the PSD data, subsequently (Figure 4). Then, using step.(8) and value of maximum energy of adsorption (Table 1), the ED was calculated from the PSD data (Figure 5). After obtaining energy distribution within the solid, the related energy at each operation pressure was determined using the proposed algorithm by using the calculated energy data, the Unilan, Toth and Sips isotherms are plotted against the experimental data in Figure 6. Due to the heterogeneous nature of adsorbent, adsorption isotherms show good behavior and are well able to predict the experimental data. A comparison between the conventional Unilan and Sips isotherms with their modifications by the proposed algorithm was done and the results are presented in Figure 7. From this figure, it is clear that the proposed algorithm improved the adsorption isotherms significantly. If the conventional isotherms are used for the heterogeneous solid adsorption systems, there would be significant errors in predict the adsorption isotherms (Figure 7). In order to better compare the accuracy of the proposed algorithm, the isotherm data points predicted by both modified and conventional Unilan and Sips models are presented in Table 2.
Case study 2
The second case study implemented the N2 adsorption data of a heterogeneous adsorbent prepared from macadamia-nutshell chemically activated with ZnCl2 chemical to nutshell ratio 5% namely NS-ZnCl2.49 Doing the same procedure as in Case 1, the PSD of the solid was obtained using linear regularization and a Gaussian function was fitted to the PSD data points (Figure 8). Using step (8) and maximum adsorption energy for this heterogeneous adsorbent (presented in Table 1), the ED of this solid was obtained from the PSD data (Figure 9). Similar to the Case Study-1, energy related to each adsorption pressure was obtained using the algorithm proposed in this study. Using the calculated energy data, the Unilan, Sips and Toth modified adsorption isotherms are obtained and the results are compared with the experimental data in Figure 10.
Case studies 3&4
In the third and fourth case studies, we have used N2 adsorption data of a macadamia nutshell and a coal based chemically activated carbons by KOH, respectively.50 Physical properties of these two activated carbons are presented in Table 3. Following the same procedure, the PSD of solids were obtained using linear regularization and a Gaussian function was fitted to the PSD data to obtain a Gaussian PSD function (Figure 11). The ED of solids is shown in Figure 12. Similar to the previous case Studies, energy related to each adsorption pressure was obtained using the proposed algorithm. Using the calculated energy data,51,52 modified adsorption isotherms are obtained and the results are compared with the experimental data in Figure 13 (Table 4) (Table 5).
In this study, a new approach for determination of energy distribution (ED) of heterogeneous adsorption systems based on the Kelvin theory of adsorption is presented. The proposed algorithm provides a procedure for reliably estimation of ED of heterogeneous adsorbents from pore size distribution (PSD) data. Moreover, following the presented approach make it possible to estimate the adsorption isotherm accurately. The advantage of the proposed algorithm is that by following such procedure it is possible to evaluate an energy related to solid pores and subsequently determine the amount adsorbed on each solid site with the identified energy. In this algorithm, the PSD of adsorbent is first determined by the method proposed by Shahsavand,26 and then by considering some assumptions (that are discussed in the theory section) and following the presented algorithm, the ED was determined.
In order to evaluate the proposed algorithm, adsorption data of four different heterogeneous cases were used for estimation of the PSD and subsequently the ED. From the results, the proposed algorithm provided better estimation of adsorption isotherms in all of the investigated cases than conventional adsorption models such as Unilan, Toth and Sips as well as good ED. The accuracy of the proposed approach is greatly depends on the accuracy of the PSD determination method; however, it could be safely applied as reliable procedure for determination of the ED of heterogeneous adsorption systems.53 On the other hand it seems that the proposed algorithm is benchmark for comparing the accuracy of different methods for calculating the PSD. Because, if the PSD achieved in the first step is not sufficiently accurate ultimately isotherms obtained will be much difference with the experimental data. This entry is being studied and will be reported in subsequent studies.54
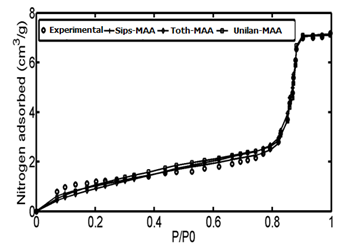
Figure 6 Comparison of experimental data with three modified isotherms; Sips- M.A.A, Unilan- M.A.A and Toth- M.A.A.
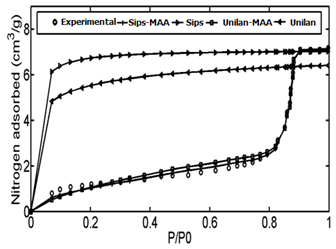
Figure 7 Comparison of experimental data with modified & unmodified isotherms; Sips, Sips- M.A.A , Unilan, Unilan- M.A.A.
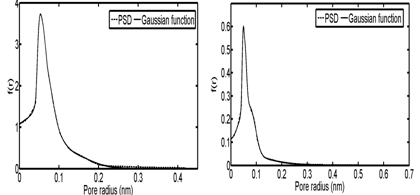
Figure 11 Pore size distribution and the fitted Gaussian functions for; (A) Coal-KOH and (B) NS – KOH.
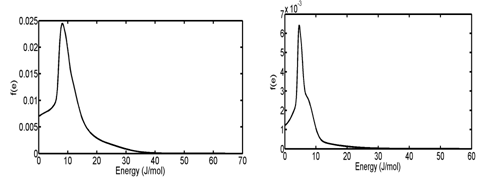
Figure 12 Energy distribution of (A) Coal-KOH and (B) NS - KOH Obtained from f(e).de = f(r).dr equation.
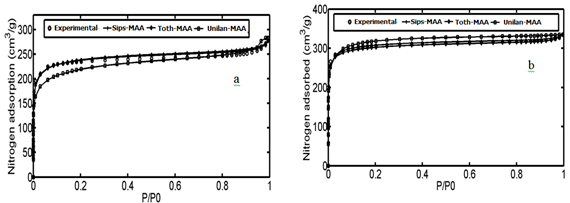
Figure 13 Comparison of experimental data with isotherm; Sips-NA, Unilan-NA, Toth-NA for; (A) Coal-KOH and (B) NS – KOH.
Emax (KJ/mol) |
Adsorbate |
Adsorbent |
NO. |
9 ≈ |
N2 |
CPG 69 |
Case 1 |
4 ≈ |
N2 |
NS-ZnCl2 |
Case 2 |
10 ≈ |
N2 |
Coal-KOH |
Case 3 |
12 ≈ |
N2 |
NS-KOH |
Case 4 |
Table 1 The maximum energy considered for different adsorbents (case 1-4))
Ci(Sips) |
Ci(Sips- M.A.A ) |
Ci(Unilan) |
Ci(Unilan M.A.A ) |
Ci(Exp.) |
Ei |
P/P0 |
No |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
6.131 |
0.618 |
4.831 |
0.507 |
0.794 |
145.0 |
0.070 |
2 |
6.379 |
0.724 |
5.058 |
0.651 |
0.980 |
163.0 |
0.098 |
3 |
6.554 |
0.837 |
5.260 |
0.807 |
1.086 |
188.0 |
0.133 |
4 |
6.671 |
0.950 |
5.427 |
0.961 |
1.129 |
218.0 |
0.172 |
5 |
6.733 |
1.031 |
5.533 |
1.068 |
1.206 |
239.0 |
0.203 |
6 |
6.780 |
1.108 |
5.622 |
1.168 |
1.237 |
262.0 |
0.234 |
7 |
6.823 |
1.200 |
5.717 |
1.284 |
1.280 |
291.0 |
0.273 |
8 |
6.848 |
1.270 |
5.776 |
1.370 |
1.282 |
320.0 |
0.301 |
9 |
6.871 |
1.336 |
5.834 |
1.449 |
1.405 |
340.0 |
0.332 |
10 |
6.899 |
1.451 |
5.914 |
1.584 |
1.397 |
390.0 |
0.381 |
11 |
6.925 |
1.589 |
5.992 |
1.739 |
1.539 |
457.0 |
0.437 |
12 |
6.938 |
1.689 |
6.039 |
1.848 |
1.582 |
510.0 |
0.457 |
13 |
6.954 |
1.794 |
6.096 |
1.959 |
1.603 |
550.0 |
0.528 |
14 |
6.965 |
1.875 |
6.137 |
2.042 |
1.721 |
580.0 |
0.570 |
15 |
6.975 |
1.972 |
6.180 |
2.139 |
1.805 |
620.0 |
0.619 |
16 |
6.986 |
2.085 |
6.216 |
2.250 |
1.907 |
680.0 |
0.664 |
17 |
6.988 |
2.148 |
6.237 |
2.310 |
2.001 |
710.0 |
0.692 |
18 |
6.992 |
2.206 |
6.254 |
2.365 |
2.066 |
740.0 |
0.716 |
19 |
6.996 |
2.257 |
6.272 |
2.413 |
2.160 |
760.0 |
0.744 |
20 |
6.999 |
2.352 |
6.288 |
2.500 |
2.317 |
820.0 |
0.769 |
21 |
7.002 |
2.470 |
6.303 |
2.607 |
2.520 |
900.0 |
0.793 |
22 |
7.005 |
2.745 |
6.320 |
2.848 |
2.798 |
1100 |
0.821 |
23 |
7.007 |
3.008 |
6.324 |
3.072 |
3.131 |
1300 |
0.828 |
24 |
7.008 |
3.694 |
6.337 |
3.638 |
3.702 |
1800 |
0.852 |
25 |
7.009 |
4.356 |
6.341 |
4.190 |
4.358 |
2300 |
0.859 |
26 |
7.010 |
4.795 |
6.346 |
4.577 |
4.767 |
2650 |
0.869 |
27 |
7.011 |
5.398 |
6.348 |
5.161 |
5.394 |
3200 |
0.872 |
28 |
7.011 |
6.033 |
6.352 |
5.892 |
6.095 |
3940 |
0.879 |
29 |
7.012 |
6.610 |
6.353 |
6.667 |
6.538 |
5010 |
0.882 |
30 |
7.014 |
7.072 |
6.364 |
7.086 |
6.988 |
7400 |
0.903 |
31 |
7.017 |
7.109 |
6.381 |
7.095 |
7.002 |
8000 |
0.938 |
32 |
7.020 |
7.115 |
6.396 |
7.096 |
7.033 |
8100 |
0.969 |
33 |
7.022 |
7.144 |
6.409 |
7.099 |
7.173 |
9000 |
0.997 |
34 |
Table 2 Comparison of isotherms data; Sips;Sips-M.A.A & Unilan; Unilan- M.A.A (C: Nitrogen adsorbed)
Sample |
T |
Activation time (min) |
Weight loss (%) |
Density (g/cm3) |
SBET (m2/g) |
Vmi (cm3/g) |
Vmeso (cm3/g) |
X0,DS† (nm) |
Coal:KOH |
973 |
120 |
26 |
0.65 |
850 |
0.388 |
0.046 |
0.57 |
NS:KOH |
973 |
60 |
75 |
0.29 |
1075 |
0.479 |
0.034 |
0.63 |
Table 3 Physical characteristics of two chemically activated carbons
| Case 1 | Case 2 | Case 3 | Case 4 | No. | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Ei |
Cµ |
P/P0 |
Ei |
Cµ |
P/P0 |
Ei |
Cµ |
P/P0 |
Ei |
Cµ |
P/P0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
3.8500 |
58.884 |
0.0000 |
6.2400 |
37.153 |
0.0000 |
14.400 |
498.20 |
0.0600 |
145.00 |
0.7940 |
0.0700 |
2 |
4.1600 |
77.625 |
0.0000 |
6.8000 |
52.481 |
0.0000 |
16.600 |
551.30 |
0.0900 |
163.00 |
0.9800 |
0.0980 |
3 |
4.4600 |
95.499 |
0.0001 |
7.1840 |
63.000 |
0.0000 |
18.900 |
586.60 |
0.1200 |
188.00 |
1.0860 |
0.1330 |
4 |
4.6200 |
107.15 |
0.0001 |
7.5400 |
72.443 |
0.0001 |
21.200 |
616.10 |
0.1500 |
218.00 |
1.1290 |
0.1720 |
5 |
4.8000 |
120.23 |
0.0001 |
8.2000 |
93.325 |
0.0001 |
22.700 |
636.70 |
0.1600 |
239.00 |
1.2060 |
0.2030 |
6 |
5.3000 |
147.91 |
0.0003 |
8.8700 |
109.65 |
0.0003 |
32.100 |
775.30 |
0.2900 |
262.00 |
1.2370 |
0.2340 |
7 |
5.8000 |
173.78 |
0.0005 |
9.7800 |
130.00 |
0.0006 |
38.000 |
843.10 |
0.3500 |
291.00 |
1.2800 |
0.2730 |
8 |
6.5000 |
194.98 |
0.0012 |
10.800 |
145.00 |
0.0013 |
49.000 |
946.30 |
0.4400 |
320.00 |
1.2820 |
0.3010 |
9 |
805.00 |
234.42 |
0.0043 |
12.700 |
173.78 |
0.0036 |
69.800 |
1040.6 |
0.5600 |
340.00 |
1.4050 |
0.3320 |
10 |
9.4000 |
266.01 |
0.0097 |
15.500 |
194.98 |
0.0096 |
161.00 |
1140.8 |
0.7800 |
390.00 |
1.3970 |
0.3810 |
11 |
12.560 |
283.83 |
0.0297 |
20.300 |
208.93 |
0.0292 |
229.00 |
1149.7 |
0.8400 |
457.00 |
1.5390 |
0.4370 |
12 |
16.000 |
294.84 |
0.0632 |
25.700 |
224.87 |
0.0611 |
426.30 |
1164.4 |
0.9100 |
510.00 |
1.5820 |
0.4750 |
13 |
18.000 |
298.62 |
0.0850 |
29.200 |
227.84 |
0.0853 |
649.40 |
1167.3 |
0.9400 |
550.00 |
1.6030 |
0.5280 |
14 |
19.550 |
300.91 |
0.1038 |
31.600 |
229.51 |
0.1031 |
984.70 |
1179.1 |
0.9600 |
580.00 |
1.7210 |
0.5700 |
15 |
21.000 |
302.99 |
0.1273 |
34.700 |
231.16 |
0.1261 |
1989.8 |
1185.0 |
0.9800 |
620.00 |
1.8050 |
0.6190 |
16 |
23.000 |
304.33 |
0.1465 |
37.300 |
232.25 |
0.1446 |
4000.0 |
1205.7 |
0.9900 |
680.00 |
1.9070 |
0.6640 |
17 |
24.600 |
305.47 |
0.1661 |
39.900 |
233.30 |
0.1647 |
- |
- |
- |
710.00 |
2.0010 |
0.6920 |
18 |
25.900 |
306.32 |
0.1835 |
42.360 |
234.09 |
0.1829 |
- |
- |
- |
740.00 |
2.0660 |
0.7160 |
19 |
27.700 |
307.14 |
0.2028 |
45.080 |
234.92 |
0.2026 |
- |
- |
- |
760.00 |
2.1600 |
0.7440 |
2 0 |
31.000 |
308.80 |
0.2487 |
52.000 |
236.53 |
0.2494 |
- |
- |
- |
820.00 |
2.3170 |
0.7690 |
21 |
36.000 |
310.30 |
0.3031 |
60.300 |
238.01 |
0.3033 |
- |
- |
- |
900.00 |
2.5200 |
0.7930 |
22 |
42.400 |
311.44 |
0.3542 |
62.000 |
239.19 |
0.3543 |
- |
- |
- |
1100.0 |
2.7980 |
0.8210 |
23 |
48.040 |
312.30 |
0.3996 |
64.000 |
240.11 |
0.4005 |
- |
- |
- |
1300.0 |
3.1310 |
0.8280 |
24 |
55.600 |
313.13 |
0.4498 |
74.000 |
241.02 |
0.4505 |
- |
- |
- |
1800.0 |
3.7020 |
0.8520 |
25 |
64.050 |
313.83 |
0.4999 |
83.960 |
241.86 |
0.5008 |
- |
- |
- |
2300.0 |
4.3580 |
0.8590 |
26 |
74.400 |
314.46 |
0.5497 |
96.770 |
242.66 |
0.5509 |
- |
- |
- |
2650.0 |
4.7670 |
0.8690 |
27 |
84.800 |
315.04 |
0.5999 |
112.42 |
243.42 |
0.6010 |
- |
- |
- |
3200.0 |
5.3940 |
0.8720 |
28 |
103.60 |
315.60 |
0.6499 |
132.35 |
244.22 |
0.6509 |
- |
- |
- |
3940.0 |
6.0950 |
0.8790 |
29 |
122.50 |
316.17 |
0.6998 |
156.54 |
245.05 |
0.7012 |
- |
- |
- |
5010.0 |
6.5380 |
0.8820 |
30 |
1601.0 |
316.66 |
0.7398 |
189.27 |
245.76 |
0.7412 |
- |
- |
- |
7340.0 |
6.9880 |
0.9030 |
31 |
169.50 |
317.06 |
0.7700 |
224.75 |
246.40 |
0.7697 |
- |
- |
- |
8100.0 |
7.0020 |
0.9380 |
32 |
197.80 |
317.51 |
0.7999 |
256.15 |
247.07 |
0.8004 |
- |
- |
- |
8400.0 |
7.0330 |
0.9690 |
33 |
226.06 |
317.89 |
0.8199 |
301.69 |
247.60 |
0.8196 |
- |
- |
- |
9000.0 |
7.1730 |
0.9970 |
34 |
254.30 |
318.27 |
0.8401 |
337.27 |
248.27 |
0.8400 |
- |
- |
- |
- |
- |
- |
35 |
292.00 |
318.68 |
0.8599 |
385.66 |
249.03 |
0.8599 |
- |
- |
- |
- |
- |
- |
36 |
329.00 |
319.06 |
0.8749 |
445.40 |
249.73 |
0.8749 |
- |
- |
- |
- |
- |
- |
37 |
381.50 |
319.51 |
0.8900 |
502.35 |
250.55 |
0.8899 |
- |
- |
- |
- |
- |
- |
38 |
442.70 |
320.01 |
0.9049 |
576.35 |
251.55 |
0.9047 |
- |
- |
- |
- |
- |
- |
39 |
571.70 |
320.86 |
0.9252 |
671.69 |
253.53 |
0.9251 |
- |
- |
- |
- |
- |
- |
40 |
821.00 |
322.21 |
0.9469 |
863.81 |
256.88 |
0.9472 |
- |
- |
- |
- |
- |
- |
41 |
1213.2 |
323.78 |
0.9640 |
1821.5 |
261.64 |
0.9638 |
- |
- |
- |
- |
- |
- |
42 |
2409.4 |
326.81 |
0.9817 |
3875.1 |
272.39 |
0.9828 |
- |
- |
- |
- |
- |
- |
43 |
12000 |
334.87 |
0.9963 |
10000 |
282.38 |
0.9933 |
- |
- |
- |
- |
- |
- |
44 |
Table 4 Calculated of energy at each pressure in different cases by algorithm M.A.A
constants |
Gaussian function |
NO. |
||||||||||||||||||||||||||||||
|
y=a1.exp[−(x−b1c1)2]+...+a7.exp[−(x−b7c7)2] |
Case 1 |
||||||||||||||||||||||||||||||
|
y=a1.exp[−(x−b1c1)2]+...+a6.exp[−(x−b6c6)2] |
Case 2 |
||||||||||||||||||||||||||||||
|
y=a1.exp[−(x−b1c1)2]+...+a7.exp[−(x−b7c7)2] |
Case 3 |
||||||||||||||||||||||||||||||
|
y=a1.exp[−(x−b1c1)2]+...+a5.exp[−(x−b5c5)2] |
Case 4 |
||||||||||||||||||||||||||||||
Table 5 The fitted Gaussian functions to PSD data and their constants
The author declares that there is no conflict of interest.

©2018 Arjmandi, et al. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.