
Research Article Volume 2 Issue 6
Effects of Non-Darcy Porous Medium on MHD Mixed Convection with Cross Diffusion and Non Uniform Heat Source/Sink over Exponentially Stretching Sheet
Prabhugouda Patil,1
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Nafisabanu Kumbarwadi1
1Department of Mathematics, Karnataka University, India
1Department of Mathematics, Karnataka University, India
Correspondence: Prabhugouda Patil, Department of Mathematics, Karnataka University, India
Received: June 24, 2017 | Published: July 17, 2017
Citation: Patil P, Kumbarwadi N. Effects of non-darcy porous medium on MHD mixed convection with cross diffusion and non uniform heat source/sink over exponentially stretching sheet. Int J Petrochem Sci Eng. 2017;2(6):178-186. DOI: 10.15406/ipcse.2017.02.00055
Download PDF
Abstract
This paper focuses on MHD mixed convection flow over an exponentially stretching vertical sheet. The effects of cross diffusion, non-uniform heat source/sink and Non-Darcy porous medium are considered. The governing nonlinear partial differential equations reduced to linear partial differential equations by utilizing implicit finite difference scheme in combination with quasi-linearization technique. Further, the impact of various governing physical parameters on velocity, temperature and concentration profiles in association with skin friction, heat transfer and mass transfer rates are analysed and discussed through graphs. The numerical results depict that non-Darcy porous medium enhances the velocity profile, skin friction and mass transfer rate while reduces the heat transfer rate. Numerical results are compared with previous available literature and found to be in excellent agreement.
Keywords: Magnetohydrodynamics (MHD), Exponentially stretching surface, Mixed convection, Cross diffusion, Non-similar solution, Non-uniform heat source/sink, Darcy-Forchheimer (Non-Darcy) porous medium
Introduction
The flow through porous medium has wide range of applications in various fields of science and engineering such as in food processing, in petroleum engineering (gas and oil production from reservoirs), chemical engineering (reactors), environmental engineering (ground water pollution by toxic liquids), civil (concrete and soil are porous medium), agricultural (drainage and irrigation), geothermal, biomedical engineering (lung, kidneys) and hydrology (aquifers), etc. Generally, a material (space) consisting of pores, cavities and void spaces is porous medium. Further, the flow through porous medium was described by Henry Darcy1 in Darcy law as the velocity is linearly proportional to the pressure gradient. It is valid only for slow incompressible laminar flow with low velocity and small porosity. At high velocities and nonlinear porosity the Darcy law is not applicable, in such a case non-Darcy or inertial effects are used to explain high velocity flow and nonlinear porosity. Thus, it is essential to incorporate the non-Darcian terms in the study of the convective transport in a porous medium. Therefore, velocity squared term is added in momentum equation to explain the high velocity flow rate which is known as Forchheimer drag parameter or inertia term. Non-Darcy porous medium on mixed convection over an exponentially stretching sheet with cross diffusion have been studied by Srinivasacharya & Ramareddy.2 The effects of doubly stratified fluid saturated non-Darcy porous medium and cross diffusion of mixed convection over vertical plate have been investigated by Srinivasacharya & Surender.3 Soret and Dufour effects in non-Darcy porous medium have been examined by Partha et al.4 Very recently, Darcy-Forchheimer flow of Viscoelastic nanofluids: A comparative study described by Hayat et al.5
In recent years, the study of MHD has received considerable attention because of its increasing applications in engineering and industrial processes, such as MHD generators, design of nuclear reactors, plasma studies, petroleum resources, nuclear industry, thermal insulation, military submarines, geophysics etc. One dimensional mixed MHD convection has been investigated by Sposito & Ciafalo .6 MHD mixed convection boundary layer flow over stretching vertical surface with constant wall temperature have been studied by Ishak et al.7 Heat and mass transfer on MHD flow over a vertical stretching surface with heat source, chemical reaction and thermal stratification effects have been explained by Kandasamy et al.8 MHD flow and heat transfer of couple stress fluid over an oscillatory stretching sheet with heat source/sink in porous medium studied by Nasir et al.9
The mass diffusion due to temperature gradient is termed as Soret effect and heat diffusion due to concentration gradient is known as Dufour effect. These effects together are also called as cross diffusion. In most of the investigation these effects are neglected because of their smaller orders of magnitude described by Fourier and Fick's laws. These effects are significant when density difference arises in the fluid flow. The Dufour and Soret (cross diffusion) effects have many practical applications such as ground water migration, the solidification of binary alloys, and in the areas of geosciences, and chemical engineering. A detailed study on cross diffusion of mixed convection flows have been provided by many authors for example Eckert and Drake,10-13 etc.
The heat and mass transfer over stretching sheet have been studied extensively in recent years because of their ever-increasing practical applications in polymer processing industry, crystal growing, drawing of plastic wires and films, food processing, paper and glass fiber production, polymer extrusions, manufacturing of artificial fibers etc. Crane 14 initiated the study of boundary layer flow over linear stretching surface. Gupta & Gupta15 have studied isothermal stretching with suction/blowing effects. Chen & Char16 extended the work of Gupta & Gupta15 to non-isothermal stretching sheet. Chen17 described an analysis of mixed convection heat transfer from a vertical continuously stretching sheet. Patil et al.18 have investigated mixed convection flow over a vertical power law stretching sheet. Patil et al.19 discussed the effects of surface mass transfer on steady mixed convection flow from vertical stretching sheet with variable wall temperature and concentration.
The heat and mass transfer through exponentially stretching sheet has many applications in science and technology such as annealing and thinning of copper wires and many more. Magyari & Keller20 discussed the heat and mass transfer characteristics of boundary layer flow over exponentially continuous stretching sheet. El-Aziz21 presented the viscous dissipation effect on mixed convection flow of a micropolar fluid over an exponentially stretching sheet. Sajid & Hayat22 examined the impact of thermal radiation on boundary layer flow due to exponentially stretching surface. Bidin & Nazar23 investigated the effects of thermal radiation on boundary layer flow over an exponentially stretching sheet. Dulal Pal24 discussed the magnetic effect on mixed convection heat transfer in the boundary layers on an exponentially stretching sheet. Ishak25 obtained the numerical solution of MHD boundary layer flow over an exponentially stretching sheet with radiation effects. Mukhopadhyay & Gorla26 have studied the effects of partial slip on boundary layer flow past a permeable exponentially stretching sheet in presence of thermal radiation. Mukhopadhyay27 studied slip effects on MHD boundary layer flow over an exponentially stretching sheet with suction/blowing and thermal radiation.
The study of viscous dissipation is transfer of kinetic energy of fluid to internal energy of the fluid. Many researchers considered the viscous dissipation effect with numerous geometries and fluid properties. For example, Dessie & Naikoti28 examined MHD effects on heat transfer over stretching sheet embedded in porous medium with variable viscosity, viscous dissipation and heat source/sink. Bhukta et al.29 discussed the dissipation effect on MHD mixed convection flow over a stretching sheet through porous medium with non-uniform heat source/sink. Very recently Patil et al.30 investigated double diffusive mixed convection flow from a vertical exponentially stretching surface in presence of the viscous dissipation.
The simultaneous effect of temperature and concentration gradient on the flow velocity is known as double diffusive. Patil et al.31 investigated thermal diffusion and diffusion-thermo effects on mixed convection from an exponentially impermeable stretching surface. The non-similarity in the flow occurs due to free stream velocity, surface mass transfer or due to curvature of the body or due to all these effects. Because of its mathematical complexity many researchers restricted (confined) their studies to either unsteady similar flows or steady non-similar flows. The study of non-similar solutions is made by Patil et al.32-34
The aim of the present paper is to explore the study of steady MHD mixed convection flow over exponentially stretching sheet in presence of cross diffusion, non-uniform heat source/sink and Darcy-Forchheimer porous medium. This work has not been reported in the literature so far to the authors best of knowledge. Non-similar transformations are used to transform the governing boundary layer equations to a set of non-dimensional equations and then numerically solved by an implicit finite difference scheme in association with the Quasi-linearization technique.35 The numerical results are compared with the previously published data, and are found to be in good agreement.
Analysis
Consider two-dimensional steady laminar MHD mixed convection flow through exponentially stretching vertical sheet embedded in Darcy-Forchheimer porous medium in presence of cross diffusion, viscous dissipation and non-uniform heat source/sink. Consider the sheet is moving vertically upward direction in x-axis and y-axis normal to it, as shown in Figure 1. A uniform magnetic field B0 is applied normal to the plate. The velocity of the wall stretching sheet is
and freestream velocity is
where
reference and
is ambient velocity. The surface (sheet) temperature
and concentration
of the fluid are constant. All thermo physical properties of the fluid are assumed to be constant except the density variations causing a body force in the momentum equation. Using Boussinesq Approximation,36 the governing equations for conservation of mass, momentum, energy and species concentration are given by
.......... (1)
....... (2)
................(3)
..................(4)
With boundary conditions:
.......................... (5)
Using the non-similar transformations:
................ (6)
From Eqs. (1) to (4), we find that Eq. (1) is trivially satisfied and Eqs. (2) to (4) reduce to
.............. (7)
.............. (8)
.................... (9)
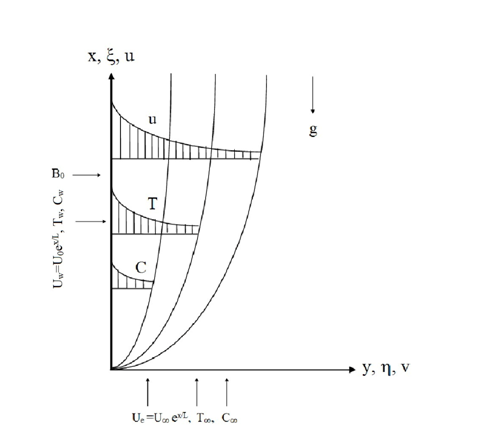
Figure 1 The Schematic flow model.
From Eq. (5), the dimensionless boundary conditions are
Here
and
Note that
denotes the impermeable plate, i. e., there is no suction or injection. The momentum Eq. (7), the temperature Eq. (8) and the species concentration Eq. (9) are coupled with each other. Further, the Richardson number Ri, which characterizes the mixed convection effects, Nrepresenting the ratio between the thermal and the solutal buoyancy forces,
is the velocity ratio parameter, Da is Darcy number,
is Forchheimer drag coefficient,
is the Dufour number and
is the Soret number and they are defined, respectively, as
and
.............. (10)
Where
is the Grashof number referring to the wall temperature
is the Grashof number referring to the wall species concentration and
is non-uniform heat source/sink. Where A* is space dependent heat source/sink and B* is temperature dependent heat source/sink. The case A* > 0 and B* > 0 corresponds to heat source (generation) and A* < 0, B* < 0 corresponds to heat sink or absorption.
Further the skin friction coefficient
, the heat transfer
and mass transfer
rates are defined as
.................... (11)
i. e.,
............... (12)
i.e.,
........... (13)
Method of solution
The arrangement of coupled nonlinear partial differential equations (7) to (9) with boundary condition (10) has been solved numerically by using the implicit finite difference scheme along with Quasi-linearization technique.36 The benefit of this system is that it has the quadratic rate of convergence. Further, using the Quasi-linearization technique the arrangement of coupled nonlinear partial differential equations (7) to (9) with boundary condition (10) is replaced by the following sequence of linear partial differential equation.
........ (14)
............... (15)
........... (16)
The coefficient functions with iterative index i are known and the functions with iterative index (i+1) are to be determined. The corresponding boundary conditions are given by
................... (17)
The coefficients in equation (14) to (16) are given by
The subsequent arrangement of linear partial differential equations (14) to (16) were discretized utilizing second order central difference formula in
-direction (boundary layer) and backward difference formula in
- direction (streamwise). At every iteration step, the equations were then transformed to a set of linear algebraic equations, with a structure of block tri-diagonal which is solved using Varga’s algorithm.37 To ensure the convergence of the numerical solution to the exact solution, a proper and optimal value for step sizes
and
have been taken as 0.001 and 0.001, respectively. Moreover, a grid independent study was carried out to examine the effect of the step size Δη and the edge of the boundary layer η∞ on the solution in the quest for their optimization. The ηmax i.e. η∞ was so chosen that the solution shows negligible changes for η larger than ηmax. A step size of Δη = 0.001 was found to be satisfactory for a convergence criteria with an absolute error less than 10-5 in all cases and the value of η∞ = 10 was found to be sufficiently large for the velocity to reach the relevant freestream velocity. The outcomes exhibited here are independent of the step sizes at least up to the fifth decimal place. A convergence criterion based on the relative contrast between the current and previous iteration values. When the difference reaches less than 10-5 at all grid points, the solution is assumed to have converged and the iterative process is terminated.
i. e.,
Max
................ (18)
To assess the accuracy of the solution, the results have been compared with the results obtained by El-Azaz,21 Ishak25 and Mukhopadhyay27 and results reveal excellent agreement as shown in Table 1.
Pr |
1 |
2 |
3 |
5 |
10 |
Ishak [25] |
0.9548 |
1.4715 |
1.8691 |
2.5001 |
3.6604 |
Swati [27] |
0.9547 |
1.4714 |
1.8691 |
2.5001 |
3.6603 |
El-Aziz [21] |
0.9548 |
--------- |
1.8691 |
2.5001 |
3.6604 |
Present study |
0.9549 |
1.4714 |
1.8691 |
2.5002 |
3.6602 |
Table 1 Values of
for varius values of Prandtl number Pr with Re = 0,
and N = 0,
In support of non-similar solutions, the numerical solutions for
,
and
are presented for various values of physical parameters as shown in Table 2.
Ec |
Da |
|
B* |
Sc |
|
|
|
-0.5 |
1 |
0.5 |
0.3 |
0.94 |
2.71344 |
9.80420 |
0.1234 |
0.0 |
1 |
0.3 |
0.3 |
0.94 |
3.61032 |
7.39947 |
0.8046 |
0.5 |
1 |
0.3 |
0.3 |
0.94 |
4.78540 |
4.50121 |
1.6111 |
0.5 |
1 |
0.3 |
0.3 |
0.94 |
4.78540 |
4.50121 |
1.6111 |
-0.5 |
|
0.3 |
0.3 |
0.94 |
4.27709 |
10.40794 |
0.0658 |
0.0 |
|
0.3 |
0.3 |
0.94 |
5.71065 |
7.55976 |
0.8893 |
0.5 |
|
0.3 |
0.3 |
0.94 |
7.83338 |
3.75340 |
1.9478 |
0.3 |
1 |
0.3 |
-0.3 |
0.94 |
4.59655 |
4.95243 |
1.4812 |
0.3 |
|
0.3 |
-0.3 |
0.94 |
7.57692 |
4.23672 |
1.8116 |
0.5 |
1 |
0.5 |
0.3 |
0.94 |
4.49791 |
5.02617 |
0.8109 |
0.5 |
|
0.5 |
0.3 |
0.94 |
7.35792 |
4.44318 |
1.1958 |
Table 2 Values of
,
,
for different values of Eckert number Ec, Darcy number Da, magnetic field M, Sr and B*with
N= 0.5
Df = 0.3,
Results and discussion
The numerical computations have been carried out for various values of
The edge of the boundary layer
has been taken between 4.0 and 10.0 based on the values of the physical parameters of the profiles.
The effect of non-similar parameter or stream wise co-ordinate
on velocity
temperature
and species concentration profiles
is displayed in Figure 2. The velocity overshoot is observed with increasing values of stream wise coordinate
while the temperature and concentration profiles decrease with increasing values of stream wise coordinate or non-similarity variable
. This is due to the fact that the stream wise coordinate act as the favourable pressure gradient in flow velocity which increases the flow rate while decreases the thickness of momentum and concentration boundary layer.
Figure 3 illustrate the variations of velocity profile distributions for different values of M,
and Da. It is clearly seen that the velocity profile increases with an increase in
. Here
is ratio of ambient velocity to the reference velocity. For
the velocity profile decreases, this is due to fact that the reference velocity
dominates over the ambient velocity
. Further for
the velocity overshoot is observed, this is due to the fact that ambient velocity
dominates over the reference velocity
. The velocity profile increases with decrease of magnetic parameter M. physically, the presence of magnetic parameter produces the Lorenz force which reduces the movement of the fluid flow. Thus velocity profile decreases. Further, the velocity profile increases with increasing values of Darcy number Da. With porous medium (Da = 1) the movement of the fluid increases which results in reduced velocity profile while in absence of porous medium
the velocity profile enhanced.
The variations of Forchheimer’s drag coefficient
and Darcy number
on velocity profile
when
are displayed in Figure 4. The velocity profile increases with decreasing values of the Forchheimer’s drag coefficient
. The physical reason is that the increase in the inertia or non-Darcy parameter intends of porous medium which resist the fluid motion, this results in reduced velocity profile. Further, the velocity profile increases in porous medium
and decreases in absence of porous medium
. Physically, the presence of porous medium reduces the velocity of the fluid.
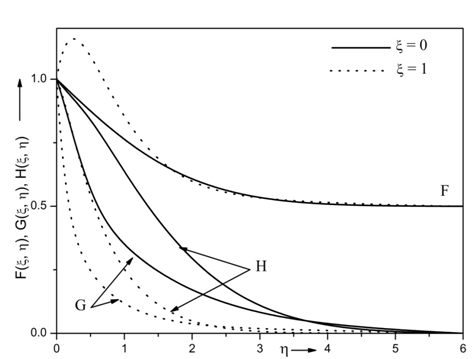
Figure 2 Effects of
on velocity profile for Re=10, Ri=10, N=0.5, Ec=0.3, Df=0.5, A*=0.3, B*= 0.3, Sr= 0.5, Sc= 0.94, M= 0.5, Da= 1, Pr= 7.0, β= 0.5,
= 1 and Г= 0.5.
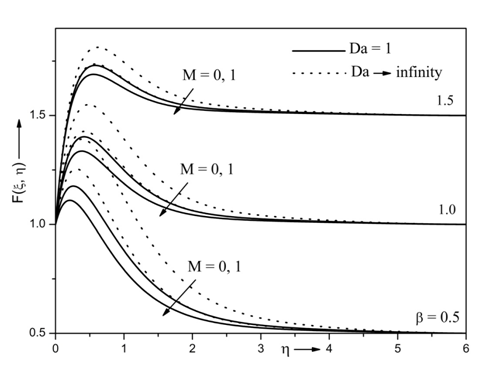
Figure 3 Effects of M, β and Da on velocity profile for Re= 10, Ri = 10, N= 0.5, Ec = 0.3, Df = 0.5, A*= 0.5, B*= 0.5, Sr = 0.5, Sc= 0.94, Pr =7.0,
= 1 and Г= 0.5
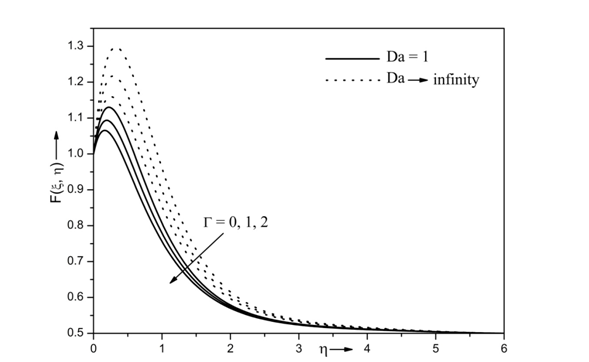
Figure 4 Effects of Г and Da on Velocity profile for Re =10, Ri= 10, N= 0.5, Ec= 0.3, Df = 0.5, A*= 0.5, B* = 0.5, Sr = 0.5, Sc= 0.94, Pr= 7.0, M =1, β= 0.5,
= 1 and Г= 0.5.
The effects of various values of Dufour number Df and magnetic parameter M on temperature profile is shown in Figure 5. Generally, Dufour number is heat diffusion due to concentration differences. It is clearly observed from Figure 5 that the velocity profile increases with increasing values of the Dufour number Df. Physically, the Dufour term occur in momentum equation which results in increased temperature profile with increasing values of the Dufour number Df. Further, the temperature profile increases with increasing values of the magnetic parameter M. This is due to fact that the inclusion of the magnetic parameter results in Lorenz force which reduces the fluid motion and enhances the temperature of the fluid. Thus, momentum boundary layer thickness and temperature profile increases.
The effects of Soret number Sr and Schmidt number Sc on species concentration profile
when
is displayed in Figure 6. The species concentration profile increases with increasing values of the Soret number Sr. Physically, the Soret number is mass diffusion due to temperature variations in the flow. In addition, the Soret number term occur in concentration which results in enhanced species concentration with increase of Soret number. Here, the realistic values of Schmidt number Sc = 0.66 and 0.94, representing the diffusion of species of most common interest such as Propyl Benzene Hydrogen and water vapour at 25˚C at one atmospheric pressure. Moreover, increase in Schmidt number decreases the species concentration profile. This is due to the fact that the increase in Schmidt number Sc means decrease of diffusivity that result in decrease of species concentration profile.
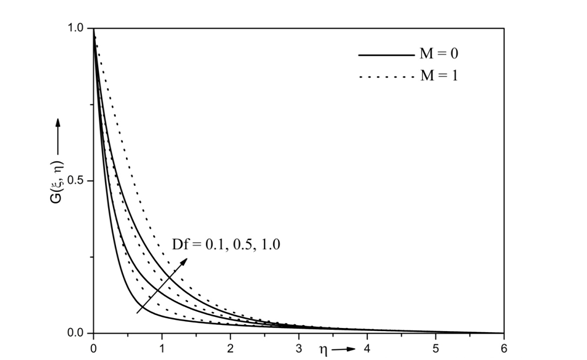
Figure 5 Effects of Df and M on temperature profile for Re =10, Ri =10, N =0.5,Ec =0.3, A* = 0.5, B* = 0.5, Sr = 0.5, Sc= 0.66, Pr = 7.0, Da =1, β = 0.5,
= 1 and Г = 0.5.
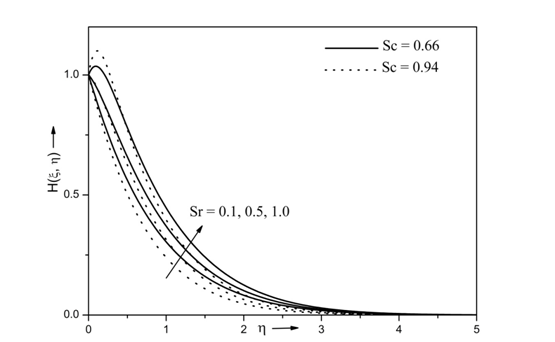
Figure 6 Effects of Sr and Sc on concentration profile for Re = 10, Ri = 10, N= 0.5, Ec= 0.3, A* =0.5, B* =0.5, Df = 0.5, M =1, Pr =7.0, Da =1, β = 0.5,
= 1 and Г = 0.5.
Figure 7 shows the effects of space dependent heat source/sink parameter A* and magnetic parameter M on skin friction coefficient
It is clearly seen that the skin friction coefficient increases with decrease of magnetic parameter. This is due to the inclusion of magnetic field in the flow region which results in a force called Lorenz force which causes to decrease the skin friction coefficient. Moreover, the skin friction coefficient increases with increase in A*. The inclusion of space dependent heat source A* has ability to increase the friction between the wall and fluid layers. Because of increase in friction, the fluid velocity is reduced and skin friction coefficient is enhanced. In particularly, for
the skin friction coefficient increases around 12% and 15% with
, respectively.
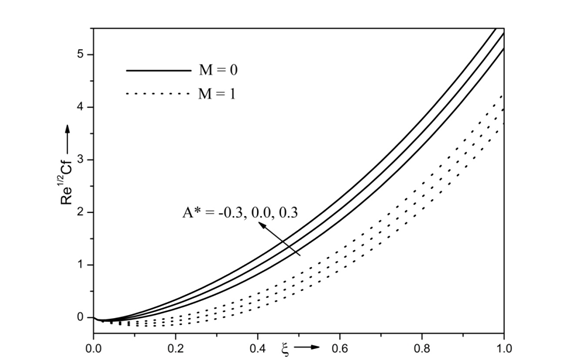
Figure 7 Effects of M and A* on skin friction coefficient for Re = 10, Ri = 10, N =0.5, Ec =0.3, B* = 0.3, Sr = 0.3, Pr =7, Da =1, Г = 0.5 and Sc = 0.94.
The effects of Eckert number Ec and Darcy number Da on skin friction coefficient
is displayed in Figure 8. It is clearly seen that the skin friction coefficient
increases with Eckert number Ec. Eckert number characterizes the viscous dissipation in which the viscosity of the fluid takes the energy from motion of the fluid and converts it into internal energy which results in enhanced heat transfer that increases the fluid motion. Thus the skin friction coefficient increases with increase in Ec. Furthermore, skin friction coefficient increases in absence of porous medium while decreases in presence of porous medium. Skin friction coefficient
increase approximately about 58% and 64% as Ec increases from
to
corresponding to the Darcy number
and
respectively.
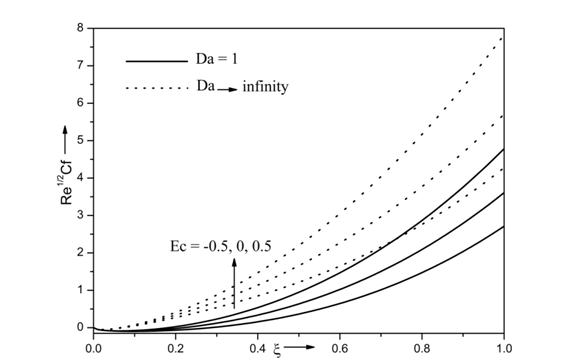
Figure 8 Effects of Ec and Da on skin friction coefficient for Re = 10, Ri = 10, N =0.5, Ec =0.5, Df =0.3, β=0.5, A* = 0.3, B*= 0.3, Sr =0.3, Pr =7, M =1, Г = 0.5 and Sc = 0.94.
The influence of temperature dependent heat source/sink B* and Darcy number Da on heat transfer rate
when
is displayed in Figure 9. It is predicted that the heat transfer rate
increases with decreasing values of B*. Physically, increase in B* increases the temperature of the fluid which results in reduce of heat transfer rate. Further, the heat transfer rate increases in presence of porous medium
and opposite impact is observed in absence of porous medium
. For instance, the heat transfer rate decreases approximately 14% and 17% as Da increase from
and
with B* = -0.3 and B* = 0.3 respectively.
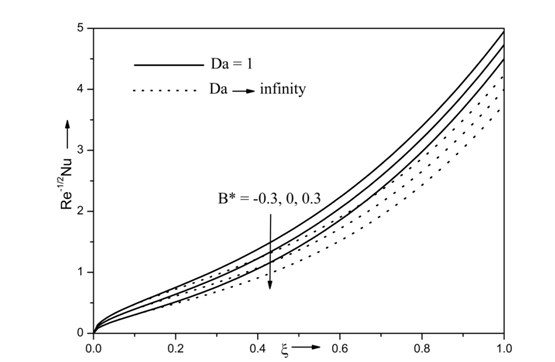
Figure 9 Effects of B* and Da on heat transfer rate for Re = 10, Ri = 10, N =0.5, Ec =0.3, Df =0.3, β=0.5, , M =1, Sr =0.3, Pr =7, A* = 0.3, Г = 0.5 and Sc = 0.94.
The effect of Soret number Sr and Darcy number Da on mass transfer rate
is shown in Figure 10. The mass transfer rate
increases with decrease of the Soret number. Soret number is temperature gradient produce a mass flux. Physically, the Soret number is linearly proportional to the temperature difference. For higher values of temperature difference, the Soret number increases which results in decrease of mass transfer rate. Further, the mass transfer rate decreases in presence of porous medium. The mass transfer rate increases about 10% with Darcy number Da increase from 1 to
respectively.
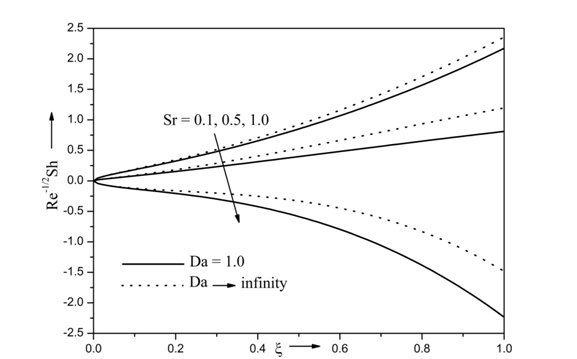
Figure 10 Effects of Sr and Da mass transfer for Re = 10, Ri = 10, N =0.5, Ec =0.5, Df =0.3, β=0.5, B*= 0.3, M =1, Pr = 7, A*= 0.3, Г = 0.5 and Sc = 0.94.
Conclusion
A numerical study is carried out for the MHD mixed convection flow over exponentially stretching surface through Darcy-Forchheimerporous medium in presence of cross diffusion (Dufour and Soret) and non-uniform heat source/sink. The resulting set of dimensionless coupled nonlinear partial differential equation was solved by using an implicit finite difference scheme in combination with Quasi-linearization technique. From this numerical investigation the following conclusions are drawn.
- The velocity profile increases in presence of porous medium as compared to absence of porous medium.
- The velocity profile decreases with increase of magnetic parameter.
- The temperature profile increases with increase of magnetic parameter.
- The skin friction coefficient increases with space dependent heat source parameter.
- In presence of porous medium the heat transfer rate increases.
- The mass transfer rate increases with increase of Darcy number.
Nomenclature
CSpecies concentration (kg m-3)
Local skin-friction coefficient
Specific heat at constant pressure (J K-1kg-1)
Concentration at the wall (kg m-3)
Reference concentration
Ambient species concentration
Dufour number
Da Darcy number
Dimensionless stream function
Dimensionless velocity
Acceleration due to gravity (ms-2 )
Dimensionless temperature
Grashof numbers due to temperature and species concentration, respectively
Dimensionless species concentration
L Characteristic length (m)
M Magnetic field parameter
N Ratio of buoyancy forces
Nusselt number
Prandtl number
Sr Soret number
Schmidt number
Temperature (K)
Temperature at the wall (K)
Reference temperature
Ambient temperature (K)
Velocity component in the
direction (m s-1)
Velocity component in the
direction(m s-1)
Cartesian coordinates (m)
Greek symbols
Thermal diffusivity (m2 s-1)
Volumetric coefficients of the thermal and concentration expansions,
respectively (K-1)
Transformed variables
Dynamic viscosity (kg m-1 s-1)
Kinematic viscosity (m2 s-1)
Density (kg m-3)
Streamfunction
Forchheimer’s drag parameter
Subscripts
w Condition at the wall
e Free stream condition
The partial derivatives with respect to these variables, respectively.
Acknowledgements
Conflict of interest
The author declares no conflict of interest.
References
- Darcy H. Les fontaines publiques de la ville de Dijon. Paris, France, 1856.
- D Srinivasacharya, Ch RamReddy. Cross–Diffusion Effects on Mixed Convection from an Exponentially Stretching Surface in Non–Darcy Porous Medium. Heat Transfer–Asian Research. 2013;42(2):111–124.
- D Srinivasacharya, O Surender. Mixed Convection Over a Vertical Plate in a Doubly Stratified Fluid–Saturated Non–Darcy Porous Medium with Cross–Diffusion Effects. Heat Transfer–Asian Research. 2014;43(8):677–690.
- MK Partha, PVSN Murthy, GP Raja Sekhar. Soret and Dufour Effects in a Non–Darcy Porous Medium. Journal of Heat transfer. 2006;128(6):605–610.
- Tasawar Hayat, Farwa Haider, Taseer Muhammad, et al. On Darcy–Forchheimer flow of viscoelastic nanofluids:A comparative study. Journal of Molecular liquids. 2017;233:278–287.
- Giuseppe Sposito, Michele Ciofalo (2006) One dimensional mixed MHD convection. International Journal of Heat and Mass Transfer. 2006;49:2939–2949.
- Anuar Ishak, Roslinda Nazar, Ioan Pop. MHD mixed convection boundary layer flow towards a stretching vertical surface with constant wall temperature. International Journal of Heat and Mass Transfer. 2010;23–24(5):5330–5334.
- R. Kandasamy, K. Periasamy, KK Sivagnana Prabhu. Chemical reaction, heat and mass transfer on MHD flow over a vertical stretching surface with heat source and thermal stratification effects. International Journal of Heat and Mass Transfer. 2005;48:4557–4561.
- Nasir Ali, Sami Ullah Khan, Muhammad Sajid, et al. MHD flow and heat transfer of couple stress fluid over an oscillatory stretching sheet with heat source/sink in porous medium. Alexandria Engineering Journal. 2016;55:915–924.
- ERG Eckert, RM Drake. Analysis of Heat and Mass Transfer. New York: McGraw Hill; 1972.
- A Postelnicu. Influence of magnetic field on heat and mass transfer from vertical surfaces in porous media considering Soret and Dufour effects. International Journal of Heat and Mass Transfer. 2004;47:1467–1472.
- T Hayat, M Mustafa, I Pop. Heat and mass transfer for Soret and Dufour’s effect on mixed convection boundary layer flow over a stretching vertical surface in a porous medium filled with a viscoelastic fluid. Commun. Nonlinear Sci Numer Simul. 2010;15:1183–1196.
- D Pal, H Mondal. Influence of chemical reaction and thermal radiation on mixed convection heat and mass transfer over a stretching sheet in Darcian porous medium with Soret and Dufour effects. Energy Convers Manage. 2012;62:102–108.
- LJ Crane. Flows past a stretching plate. Z Angew Math Phys (ZAMP). 1970;21(4):645–647.
- PS Gupta, AS Gupta. Heat and mass transfer on a stretching sheet with suction or blowing. Can J Chem Eng. 1977;55(6):744–746.
- CK Chen, MI Char. Heat transfer of a continuous stretching surface with suction or blowing. J Math Anal Appl. 1988;135:568–580.
- CH Chen. Laminar mixed convection adjacent to vertical, continuously stretching sheets. Heat Mass Transfer. 1998;33(5–6):471–476.
- PM Patil, S Roy, AJ Chamkha. Mixed convection flow over a vertical power law stretching sheet. Int J Numer Methods Heat Fluid Flow. 2010;20(4):445–458.
- PM Patil. Effects of surface mass transfer on steady mixed convection flow from vertical stretching sheet with variable wall temperature and concentration. Int J Num Heat Fluid Flow. 2012;22(3):287–305.
- E Magyari, B Keller. Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface. J Phys D:Appl Phys. 2000;32(5):577–585.
- MA El–Aziz. Viscous dissipation effect on mixed convection flow of a micro polar fluid over an exponentially stretching sheet. Canadian Journal of Physics. 2009;87(4):359–368.
- M Sajid, T Hayat. Influence of thermal radiation on the boundary layer flow due to an exponentially stretching sheet. Int Comm Heat Mass Transfer. 2008;35:347–356.
- B Bidin, R Nazar. Numerical solution of the boundary layer flow over an exponentially stretching sheet with thermal radiation. Eur J Sci Res. 2009;33(4):710–717.
- Dulal. Pal. Mixed convection heat transfer in the boundary layers on an exponentially stretching surface with magnetic field. Appl Math Comput. 2010;217:2356–2369.
- A Ishak. MHD boundary layer flow due to an exponentially stretching sheet with radiation effect. Sains Malaysiana. 2011. 40:391–395.
- S Mukhopadhyay, RSR Gorla. Effects of partial slip on boundary layer flow past a permeable exponential stretching sheet in presenceof thermal radiation. Heat Mass Transfer. 2012;48(10):1773–1781.
- Swati Mukhopadhyay. Slip effects on MHD boundary layer flow over an exponentially stretching sheet with suction/blowing and thermal radiation. Ain Shams Engineering Journal. 2013;4:485– 491.
- Hunegnaw Dessie, Naikoti Kishan. MHD effects on heat transfer over stretching sheet embedded in porous medium with variable viscosity, viscous dissipation and heat source/sink. Ain Shams Engineering Journal. 2014;5:967–977.
- D Bhukta, GC Dash, SR Mishra, et al. Dissipation effect on MHD mixed convection flow over a stretching sheet through porous medium with non–uniform heat source/sink. Ain Shams Engineering Journal. 2015.
- PM Patil, DN Latha, S. Roy, et al. Double diffusive mixed convection flow from a vertical exponentially stretching surface in presence of the viscous dissipation. International Journal of Heat and Mass Transfer. 2017;112:758–766.
- PM Patil, S Roy, E Momoniat. Thermal diffusion and diffusion–thermo effects on mixed convection from an exponentially impermeable stretching surface. International Journal of Heat and Mass Transfer. 2016;100:482–489.
- PM Patil, S Roy, I Pop. Flow and Heat Transfer over a Moving Vertical Plate in a Parallel Free Stream:Role of Internal Heat Generation or Absorption. Chemical Engineering Communications. 2012;199(5):650–658.
- PM Patil. Effects of thermophoresis on mixed convection flow from a moving vertical plate in a parallel free stream in the presence of thermal radiation. IOSR Journal of Mathematics. 2013;7(4):82–92.
- PM Patil. Chemical reaction effects on free convective flow of a polar fluid from a vertical plate with uniform heat and mass fluxes. IOSR Journal of Mathematics. 2013;6(5):66–85.
- K Inouye, A Tate. Finite difference version Quasi–linearization applied to boundary layer equations. AIAA J. 1976;12(4):558– 560.
- H Schlichting, K Gersten. Boundary Layer Theory. New York, USA: Springer; 2000.
- RS Varga. Matrix Iterative Analysis. USA: Prentice Hall; 2000.

©2017 Patil, et al. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.










