Rainfall intensity-duration-frequency (IDF) models for Uyo City, Nigeria

doi:10.15406/ijh.2017.01.00012

International Journal of

eISSN: 2576-4454

Hydrology

Research Article Volume 1 Issue 3

Rainfall intensity-duration-frequency (IDF) models for Uyo City, Nigeria

Ify L Nwaogazie,

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Martin C Ekwueme

Department of Civil and Environmental Engineering, University of Por1t Harcourt, Choba, Nigeria

Correspondence: Ify L Nwaogazie, Department of Civil and Environmental Engineering, University of Por1t Harcourt, Choba, Nigeria

Received: September 01, 2017 | Published: September 15, 2017

Citation: Nwaogazie IL, Ekwueme MC. Rainfall intensity-duration-frequency (IDF) models for Uyo city, Nigeria. Int J Hydro. 2017;1(3):63-66. DOI: 10.15406/ijh.2017.01.00012

Download PDF

Abstract

Suitable rainfall-Intensity-Duration-Frequency (IDF) models for Uyo City were developed using the statistical method of least-squares. A total of 18 rainfall models were developed based on 10 years rainfall data. These models are categorically grouped into two sets. The first set contains 10 rainfall models which represent inverse relationship between rainfall intensities and duration for specified frequencies called Intensity-Duration-Models. The second set contains 8 rainfall models which represent rainfall intensities and frequencies for specified duration called Intensity-Frequency Model. The two sets of models developed in this research recorded high and positive values of coefficient of correlation, an indication of good curve fitting with values of Intensity-Duration Models ranging from 0.948 to 0.977 and intensity frequency model ranging from 0.641 to 0.938. These set of models developed will serve as valuable tools for predicting rainfall events in Uyo City as well as for use in the design of hydraulic structures, urban drainage and flood control.

Keywords: Rainfall modeling, Intensity, Duration, Frequency, Least squares, Uyo City

Introduction

Rainfall models can be expressed mathematically to represent a relationship between Intensity, Duration & Frequency (IDF). An IDF model provides the basic probabilistic rainfall information for runoff estimation and establishes a statistical basis for design, using the return period as the measure of frequency of failure.¹⁻⁴ The IDF curves are standard tools of hydrologic risk analysis and design. Rainfall of a place can be completely defined if the intensities, durations and frequencies of the various storms occurring at that place are known. A major problem in rainfall analysis is the interpretation of past record of rainfall events in terms of future probabilities of occurrence.^5,6 Whenever an intense rain occurs, its magnitude and duration are generally known from the meteorological readings. This available data can be used to determine the frequencies of the various rains usually referred to as frequency analysis. The frequency-data for storms of various durations so obtained can be represented by Intensity-Duration-frequency Curves. Due to unavailability of rainfall data in most developing countries like Nigeria, rainfall frequency studies are very limited with only few meteorological stations usually at airport across the country. All stations where records exist, because of equipment failures continuous records for upwards of 30 years is very rare.⁵ Thus, the need for engineers to analyze available data more critically for proper planning and design of hydraulic structures is very necessary.^7,8The aim of this study is to develop and calibrate two sets of rainfall models using observed rainfall amounts and durations. The first is the intensity- duration model of quotient formula while the second is the intensity-return period model of power law. The developed models are to find great application in design of storm-water drains, culverts, erosion protection structures, etc.

Materials and methods

Study area: Uyo city is the state capital of Akwa Ibom, strategically located within the oil rich Niger Delta Southern of Nigeria and bounded to the South by Atlantic Ocean. It has coordinates of latitude 5⁰2’N and longitude 7⁰55’E and it is situated at elevation 45 meters above mean sea level (Figure 1).

Figure 1 Map of study area, Uyo Nigeria.

Data collection: The rainfall data for Uyo City were obtained from the archives of the meteorological observatory, Department of Oceanography and Regional Planning, University of Uyo. The rainfall data obtained covered the period between 2002 and 2011.

Data analysis: Selected rainfall durations of 15, 30, 45, 60, 90, 120, 180 and 300 minutes were extracted from the rainfall data and the maximum intensities computed from Equation (1).

$i = \frac{A}{t}$ (1)

Where i: Intensity in mm/hr; A: Amount of rainfall in mm; t: Duration of rainfall in hours

The resulting intensity values evaluated from Equation (1) are ranked in decreasing order of magnitude such that the largest value is assigned 1. Return period is then computed using the Weilbull’s plotting position formula⁹ as:

$P (x_{m}) = \frac{m}{n + 1}$ (2)

Where: $P (x_{m})$ Probability of exceedence of variate x_m; m: Rank of descending values with largest equal to 1; n: Number of years of record

Rainfall intensities and durations are tabulated against selected frequencies of 1.1, 1.22, 1.38, 1.57, 1.83, 2.2, 2.75, 3.7, 5.5 and 11 years. Next, the inverses of intensities were obtained to establish the relationship between rainfall intensity and duration for specified frequency.

Results

Intensity-duration quotient models: Frequencies of rainfall events calculated as the reciprocal of their corresponding probabilities are as presented in Table 1. Many formulas have been proposed in the past to fit rainfall-Intensity-Duration-Frequency Curves, but most of them are in a form with intensity inversely proportional to duration.^5‒10 The quotient model was used for the development of relationship between intensity of rainfall and its duration at specific return period. The quotient model is given by⁹as;

$i = \frac{a}{t + b}$ (3)

Where i: rainfall intensity (mm/hr); t: rainfall duration (hr); a, b: regional constants

Equation (3) is linearized by taking its reciprocal to become Equation (4):

$y = a_{0} + a_{1} x$ (4)

Where: $y = 1 / i;$

$a_{0} = b / a; a_{1} = 1 / a .$

Equation (4) was solved using regression analysis via XLSTAT to produce the intensity duration models shown in Table 2. The rainfall intensity duration curves are shown in Figure 2. Apparently, the quotient model was calibrated by using the rainfall data on intensities and durations (Table 1) to obtain the regional constants of and in Equation (3) as presented in Table 3.

Intensity-return period power models: The power model was employed in developing relationship between rainfall intensity and return period at specified duration. The power model⁵is given by:

$i = a R^{b}$ (5)

Where I, rainfall intensity (mm/hr); R, return period (years); &, regional constants

Equation (5) is linearized by logarithmic approach, viz;

$\log i = \log a + b \log R$ (6)

Where: $a_{1} = b a n d a_{0} = \log a$

Regression analysis was equally employed to solve and calibrate Equation (6) using data from (Table 1) to produce the rainfall intensity-frequency models shown in Table 2. The Intensity Frequency Curves are shown in Figure 3.

S/No	Rainfall intensity, mm/hr								Ranking	Frequency
	duration, minute
	15	30	45	60	90	120	180	300
1	172.573	124.663	86.427	121.83	87.0773	61.1585	56.211	41.9269	1	11
2	163.409	119.978	82.8496	112.5281	85.0476	59.8105	53.0503	38.80302	2	5.5
3	151.708	104.28	78.864	100.342	83.4075	57.7255	51.777	38.2766	3	3.7
4	139.422	98.4352	73.3573	91.2015	80.5089	54.0191	51.1037	35.9584	4	2.75
5	128.458	92.7854	68.7327	85.167	79.2747	52.0555	49.9207	35.4334	5	2.2
6	119.173	82.7512	64.6732	79.2391	74.2752	49.7316	49.1423	30.06	6	1.83
7	108.857	74.9842	59.8449	70.5582	65.5146	48.1305	47.1733	27.9932	7	1.57
8	98.6088	67.3948	56.9279	62.77	60.8361	44.1305	46.2993	26.2766	8	1.38
9	51.1012	40.5122	34.7056	30.1114	34.9794	24.611	24.4176	17.9222	9	1.22
10	33.258	22.2692	19.1185	18.3389	19.113	10.76755	9.7309	4.9919	10	1.1

Table 1 Rainfall ranking and corresponding intensity

S/No	Duration	Intensity frequency model*	Parameters ±
1	15	$i = 89.4829 R^{0.3374}$	CC: 0.920
			GF: 0.846
2	30	$i = 60.1672 R^{0.3758}$	CC: 0.914
			GF: 0.836
3	45	$i = 53.804 R^{0.2396}$	CC: 0.641
			GF: 0.886
4	60	$i = 56.1293 R^{0.3884}$	CC: 0.929
			GF: 0.864
5	90	$i = 58.7314 R^{0.2173}$	CC: 0.850
			GF: 0.722
6	120	$i = 42.1231 R^{0.1952}$	CC: 0.902
			GF: 0.821
7	180	$i = 44.4672 R^{0.1090}$	CC: 0.938
			GF: 0.881
8	300	$i = 17.9242 R^{0.4824}$	CC: 0.703
			GF: 0.494

Table 2 Summary of all intensity-return period power models

*Intensity-Frequency models same as Intensity-Return period power model.
 Regression parameters: CC, Coefficient of Correlation; GF, Goodness of Fit

S/N	Frequency	Intensity duration model	Parameters ±
1	11	$i = \frac{16393.4}{t + 106.213}$	CC: 0.948
		$i = \frac{15060.2}{t + 99.247}$	GF: 0.898
2	5.5		CC: 0.970
			GF: 0.942
3	3.7	$i = \frac{15479.9}{t + 114.721}$	CC: 0.969
			GF: 0.939
4	2.8	$i = \frac{14881}{t + 118.601}$	CC: 0.966
			GF: 0.934
5	2.2	$i = \frac{15432.1}{t + 135.185}$	CC: 0.959
			GF: 0.920
6	1.8	$i = \frac{14513.8}{t + 135.849}$	CC: 0.958
		$i = \frac{12285}{t + 119.533}$	GF: 0.918
7	1.57		CC: 0.963
			GF: 0.928
8	1.38	$i = \frac{11890.6}{t + 145.66}$	CC: 0.954
			GF: 0.910
9	1.22	$i = \frac{8695.65}{t + 190.87}$	CC: 0.955
		$i = \frac{1776.2}{t + 34.94}$	GF: 0.913
10	1.1		CC: 0.977
			GF: 0.955

Table 3 Uyo City rainfall intensity-duration models for specified frequencies

 Rainfall intensity is given in mm/hr and duration in minutes
Regression parameters: CC, Coefficient of Correlation; GF, Goodness of Fit

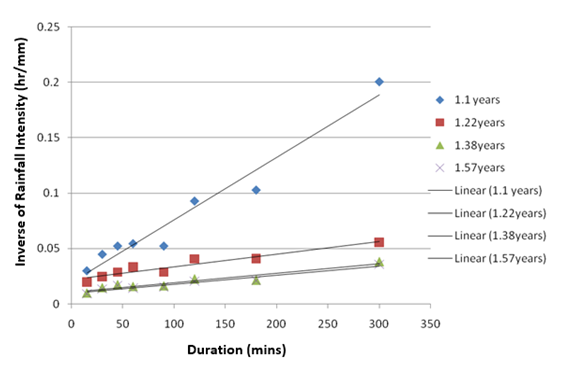
Figure 2 Inverse of Rainfall Intensity duration curves for specified frequencies for Uyo City.

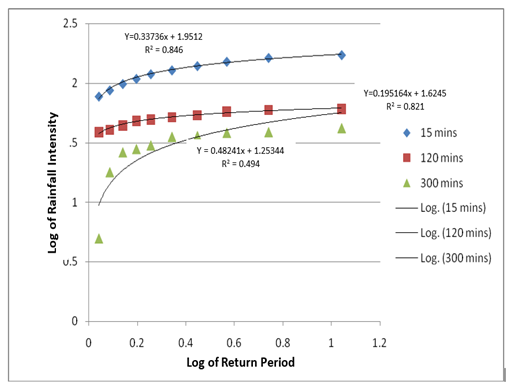
Figure 3 Rainfall Intensity return period power model for specified durations, option -1.

Discussion

The first set of rainfall models involved finding solution of the quotient formula of Equation (3) using available rainfall intensity duration data for specified frequencies of 1.1-11 years. A total of 10 rainfall models were developed as presented in Table 3 with high and positive values of coefficient of correlations of 0.948 to 0.977. The second set of rainfall models involved finding solution of the power model of Equation (5) using rainfall intensities frequency data for specified durations of 15-300 minutes. A total of 8 models were obtained as presented in Table 2 with moderate to high positive values of coefficients of correlation of 0.641 to 0.938 indicating good curve fittings. The plots of intensities against duration for the specified frequencies in Figure 2 and intensities against frequencies for the specified durations in Figure 3 formed a good basis for the predicted results. On the basis of these plots, Uyo city rainfall pattern can be characterized by the following observations. a. The curves are parallel; they do not cross each other; b. High and positive values of coefficients of correlation indicate best curve fittings; c. Higher return periods correspond with higher rainfall intensities for a given duration.¹¹

Conclusion

Based on the results of this study the following conclusion can be drawn:

The IDF models for Uyo City and their graphical equivalents have been developed from extracted rainfall data subjected to regression analyses which gave high and positive coefficient of correlation values as indication of good curve fitting.
The IDF models as derived are similar to those encountered in Engineering practice which will serve as valuable and reliable tools for engineers and hydrologists for predicting rainfall events as well as basic rainfall information for design of drains in Uyo City.