Singular oscillators’ amplitude-period aproximation

doi:10.15406/ijbsbe.2020.06.00183

International Journal of

eISSN: 2573-2838

Biosensors & Bioelectronics

Short Communication Volume 6 Issue 2

Singular oscillators’ amplitude-period aproximation

Andres Garcia,

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Andrés Roteta Lannes

Universidad Tecnologica Nacional, Argentina

Correspondence: Andres Garcia, Grupo de Investigacion en Mecanica Aplicada (GIMAP), Universidad Tecnologica Nacional. 11 de Abril 461, Bahia Blanca, Argentina

Received: October 30, 2019 | Published: March 2, 2020

Citation: García A, Lannes AR. Singular oscillators’ amplitude-period aproximation. Int J Biosen Bioelectron. 2020;6(1):25-26. DOI: 10.15406/ijbsbe.2020.06.00183

Download PDF

Abstract

Second order singular oscillators are considered and approximated. The amplitude-period relationship is determined and compared with the formulas in (10) and (11). The approximations show a great exactness and open a wide range of applications based upon singular nonlinear oscillators.

Keywords: optimal control, nonlinear oscillator, amplitude-period formula

Introduction

Many mechanical systems are modeled as nonlinear oscillators.¹ Among the many important properties that can be studied for a nonlinear oscillator, the amplitude-period relationship is a very salient one.^2‒5 As pointed out in,⁶ the singular harmonic oscillator became a classic study object from quantum physics. Accordingly, this kind of oscillators was traditionally approximated with several methods: power series, algebraic methods or even integrating its trajectories. However, more recently, other methods were explored to study singular oscillators: Fourier transform, or even Laplace transform.⁷ Besides the variety of available methods to study singular oscillators, the exact determination of their amplitude-period relationship is rather involved and for some cases even powerful approximation techniques could fail to obtain an accurate result.^8,9 In this paper, the approximation formula derived in¹⁰ and¹¹ is used to obtain and approximate the amplitude-period relationship of two nonlinear and singular oscillators: ${\overset{. .}{x} (t) = - \frac{1}{x (t)}, \overset{. .}{x} (t) = - \frac{1}{x {(t)}^{3}}}$

Singular oscillators: $\ddot{x} = - \frac{1}{x}$ and $\ddot{x} = - \frac{1}{x^{3}}$

The case of $\ddot{x} = - \frac{1}{x}$

Let’s assume a nonlinear second order oscillator given by:

$\overset{. .}{x} (t) = - \frac{1}{x (t)}, x (T) = x (0) = A, \dot{x} (0) = 0$ (1)

Where A is the oscillation’s amplitude with period T. The exact amplitude-period formula is known:²

$T_{exact} = 2. \sqrt{2. π} . A$ (2)

On the other hand, applying the formula in (10) and (11):

$T_{approx .} = 2. π \sqrt{\frac{A^{N + 2}}{(N + 2) . \int_{0}^{A} x^{N} . \frac{1}{x} . dx}} = 2. π . A \sqrt{\frac{N}{N + 2}}$ (3)

To measure the accuracy of the approximation, the quotient between (2) and (3) can be evaluated:

Exactitude (%) = \frac{2. \sqrt{2. π} . A}{2. π . A \sqrt{\frac{N}{N + 2}}} = \sqrt{\frac{π . N}{2. (N + 2)}}

Utilizing the suggested value N=3 in (10):

Exactitude (%) = \sqrt{\frac{π .3}{10}} = 97.08 %

The case of $\ddot{x} = - \frac{1}{x^{3}}$

This singular oscillator occurs for instance modeling mechanical systems with central forces:^12,13

$\dot{x} (t) = - \frac{1}{x {(t)}^{3}}, x (T) = x (0) = A, \dot{x} (0) = 0$ (4)

Then, the mechanical’s energy conservation leads the exact amplitude-period:^2,12

\dot{x} {(t)}^{2} - \frac{1}{x {(t)}^{2}} = constant

Integrating between 0 and A, with the initial conditions in (4):

\dot{x} {(t)}^{2} - \frac{1}{x (t)^{2}} = - \frac{1}{A^{2}} \Rightarrow \dot{x} (t) = \sqrt{(- \frac{1}{A^{2}} + \frac{1}{x {(t)}^{2}})} \Rightarrow T_{exact} = 4. A^{2}

The approximation using (10) and (11) yields:

T_{approx .} = 2. π . A^{2} \sqrt{\frac{N - 2}{N + 2}}

It is useful to plot the exactitude vs N:

According to Figure 1, the optimal value will be N=5, with the very precise approximation of 97.25%.

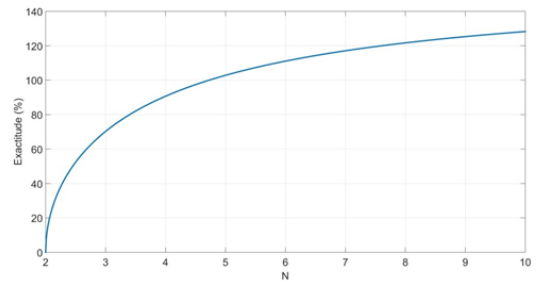
Figure 1 Approximation’s exactitude.

Conclusion

In this paper, two singular oscillators were considered using the approximating formulas presented in¹⁰ and [11]. Even with several methodologies available for nonlinear oscillators, singular oscillators are less considered in the literature. The case of singular oscillators restrict the applicability of some methods or become imprecise others, this motivates the application and analysis of simple method able to predict the amplitude-period relationship accurately. The first nonlinear oscillator considered was precisely approximated (97% of accuracy with respect the true amplitude-period formula) applying the formula in 10 with the integer parameter needed N=3, whereas for the second inverse cubic oscillator, the same formula predicts the amplitude-period better with the natural number N=5 (97.25% of accuracy). As a future work, research involving a generalization of the number N to the real set will be conducted. As it can be depicted from this paper, singular oscillators’ approximations using amplitude-period formulas are a very interesting applied research area.