Displacement energy of the two variable-length element biomechanical exoskeleton supporting leg

doi:10.15406/ijbsbe.2021.07.00223

International Journal of

eISSN: 2573-2838

Biosensors & Bioelectronics

Mini Review Volume 7 Issue 4

Displacement energy of the two variable-length element biomechanical exoskeleton supporting leg

Blinov AO,¹ Borisov AV²

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

¹Department of Technological machines and equipment, Branch of the National Research University “MPEI” in Smolensk, Russia
²Department of Higher Mathematics, Branch of the National Research University “MPEI” in Smolensk, Russia

Correspondence: Andrey V Borisov, Department of Higher Mathematics, Branch of the National Research University “MPEI” in Smolensk, 214013, Russian Federation, Smolensk, Energetichesky proezd, building 1, Russia

Received: August 26, 2021 | Published: September 23, 2021

Citation: Blinov AO, Borisov AV. Displacement energy of the two variable-length element biomechanical exoskeleton supporting leg. Int J Biosen Bioelectron. 2021;7(4):113-114. DOI: 10.15406/ijbsbe.2021.07.00223

Download PDF

Abstract

The article discusses a spatial model of two links of variable length of an active biomedical exoskeleton that simulate a supporting leg. Each hinge has drives that provide the necessary turns with the relative rotational movement of the links. The difference between the proposed model and those previously studied is the use of the angles between the links, which corresponds to the real operation of the drives. The paths of the links are set kinematically. The control forces are determined in the model from the compiled system of differential equations of motion. The calculation of energy consumption during the single-support phase of movement for one step is carried out. The application of the proposed model in the form of two links of variable length of the active biomedical exoskeleton can be found when selecting a battery for the autonomous operation of the biomedical exoskeleton.

Keywords: active biomedical exoskeleton, link of variable length, angles between links, differential equations of motion, control, force, moment of force, drive

Introduction

As a rule, the anthropomorphic robot simulation researches deal with 2-D models and use angles calculated from the vertical,^1–4 and horizontal.^5–8 This angle calculation approach can be easily applied to anthropomorphic mechanism motion simulation. It can also be used for studying many tasks, such as link motion trajectory synthesizing and Cauchy problem solving for the given control. Nevertheless, the angle calculation becomes difficult when it comes to developing an engineering design for anthropomorphic mechanism model, such as an active exoskeleton with electric drives and gears ensuring relative rotation in joints of the human motor system. The angles between the mechanism links should be found out by the model designer in this case, since these angles are altered by the electric drive actions. The causes leading to variable-length link exoskeleton model are examined in the research.⁸

Model

Let’s examine a two-links exoskeleton model. We’ll calculate the angles between the links. The model with the introduced local system of coordinates is shown in the Figure 1. The fixed right-hand Cartesian system Oxyz, in which the mechanism motion takes place, is also shown in the Figure 1. The mobile local system Ox₁y₁z₁ is fixed on the link. The axis Oz₁ is directed along the link; the other two axes correspond to the right-hand basis rule. The angle corresponding to the first link is the one between the axis of the fixed and mobile coordinate systems. The angles a₁(t), b₁(t), g₁(t) in the Figure 1 are the angles between the axes of the fixed and local systems. These angles are calculated in the negative direction. Assume a link model consisting of the two absolutely rigid weighty sections. A relative motion of the sections can take place along the А₀А₁ line connecting the section beginning and the end (Figure 1). The spherical joint in the point А₀ is fixed to the supporting surface. The relative motion of the C₁А₁ and А₀B₁ sections along the А₀А₁ line is ensured due to gravity, surface reaction force and reactions of the adjacent rods (not shown in the Figure 1). This allows for the length-changing of the B₁C₁ section and, as a result, of the entire А₀А₁ link. The А₁А₂ link design is similar to that of А₀А₁. The absolutely rigid inertial link sections A₀B₁, C₁A₁, A₁B₂, C₂A₂ are represented with bold thick lines. The variable-length and weightless sections B₁C₁ = ξ₁(t), B₂C₂ = ξ₂(t) are represented with thin lines.

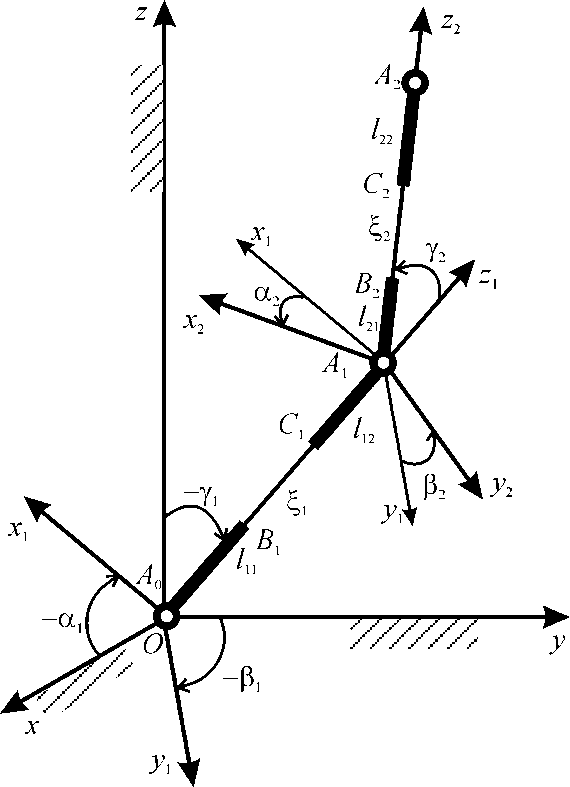
Figure 1 Model of two variable-length biomedical exoskeleton links with the angles calculated between the links.

The angles between the corresponding axes j_i, b_i, g_i_-1 (i = 1,2) and the lengths of the weightless link sections ξ_i (i = 1,2) are used as the generalized coordinates for mechanism state description (Figure 1). Since the described mechanism has seven degrees of freedom, it requires the same number of drives for organizing the controlled motion: one drive per each rotation angle and one drive for each link’s length change.

Methods

Energy functionals used in biomechanics to assess the work done in one step

$A = \int_{0}^{T} \sum_{i = 1}^{n} | Q_{i} {\dot{q}}_{i} | d t$ , (1)

$A = \frac{1}{T} \int_{0}^{T} \sum_{i = 1}^{k} | M_{i} | d t$ (2)

Here T – is the time of one step, Q_i – are the generalized forces, ${\dot{q}}_{i}$ – generalized speeds, n – is the number of degrees of freedom, M_i are the moments developed by the electric motors of the apparatus, k – is the number of electric motors. The main hypothesis when using functionals (1) and (2) is that the braking processes require energy consumption, since the energy recovery mode is not used in biomechanical systems, when the electric motor turns into a generator during braking and returns energy to the system.

Results

As a result of applying the formula (2) to the calculation of the energy costs of the motors that rotate the link and the formula (2) to the engines providing the change in the link length, we obtain the results presented in Table 1.

Drive, work designation	Energy consumption, J
А₁_a	36.10
А₂_a	1.34
А₁_b	40.73
А₂_b	37.76
А₁_g	37.78
А₂_g	0.00
А₁_F	0.07
А₂_F	1.42
А₁_a + А₂_a + А₁_b + А₂_b + А₁_g + А₂_g + А₁_F + А₂_F	155.20

Table 1 Energy costs in the drives of the mechanism

Discussion

As a result of the study, a model of two links of variable length of the active biomedical exoskeleton in space with the angles measured between the links was proposed. The estimates of the energy consumption for the model of the active exoskeleton were obtained, which amounted to 155.2 J. This model can be used to select a battery for the autonomous operation of the biomedical exoskeleton.

Conclusion

The proposed model of the mechanism is applicable for the motion compensation of the people suffering from the motor system disorders, restoring or completely replacing the motor system functions of the disabled persons. It can be applied in medicine for the rehabilitation of patients, for training muscles, restoring broken neural connections, for example, in post-stroke patients.