Three simple empirical models were proposed to predict surface tension, specific weight, and kinematic viscosity of water as a function of temperature. The formulations were derived within the framework of the nonlinear regression analysis based on the Richardson’s extrapolation method and the Levenberg–Marquardt algorithm. The estimations were proven to be satisfactory with very high determination coefficients above 0.999. The proposed formulations were developed using a total of 155 data points and compared against different equations from the literature. Moreover, illustrative examples and relevant MATLAB^® scripts were presented to demonstrate the applicability of the present equations. The statistical results clearly corroborated that the proposed equations were accurate enough to be used in estimation of the present fluid mechanics-related parameters. The computational analysis yielded simple mathematical structures to be easily used for educational and practical purposes.

Keywords: fluid mechanics, surface tension, specific weight, kinematic viscosity, water, temperature, nonlinear regression, statistical analysis

Surface tension (σ_s in N/m or kgf/m in meter-kilogram-second (MKS) unit system)¹ is resulted from the attraction effect between the molecules of the liquid due to various intermolecular forces.^2,3 Because of this effect, the surface layer of the liquid behaves like a stretched elastic membrane that allows the insects (e.g. water strider, some spider species) to walk on the liquid and causes capillary action. Moreover, a change in temperature (T in°C or K) causes a change in surface tension of a liquid. When temperature increases, kinetic energy of liquid molecules increases, resulting a decrease in intermolecular forces. Thus, surface tension decreases with increase in temperature.² The weight per unit volume of a substance is called the specific weight γ (in kgf/m³) and is determined from γ=ρg, where g is the acceleration of gravity (9.807m/s²) and ρ (in kgf.s²/m⁴) is density.^4,5 In MKS unit system, the specific weight of water at 4°C is approximately 1000kgf/m³, and the density (mass density or specific mass) is about 101.97kgf.s²/m⁴. When the temperature changes from either greater or less than 4°C, the density will become less than this value. Water has the maximum density only when it is pure water. Other factors influence water's density such as whether it is tap or fresh water or saltwater, and these variations of water changes its density.⁶ A liquid can be considered to consist of molecular layers superimposed on one another. Although the liquid flows when a shear force is applied, however, the frictional forces between the fluid layers (e.g. two parallel layers moving in a liquid) provide a resistance to this flow. Therefore, viscosity (μ in kgf.s/m² or ν in m²/s, respectively, for dynamic and kinematic viscosity) can be described as a magnitude of the resistance of a fluid to deformation under shear stress.^2–5 In fluid mechanics, the ratio of dynamic viscosity (μ) to density (ρ) appears frequently. For convenience, this ratio is given the name kinematic viscosity (ν) and is expressed as ν=μ/ρ.^4,5 It is noted that models for estimating liquid viscosities are much less derived than for gases, and their implementation is restricted to a qualitative definition. The behaviour of liquids is noticeably different from gases, and the viscosity decreases with increasing temperature for the liquids. This relationship can be mostly expressed in the form of an Arrhenius-type formulation. The surface tension, specific weight, and kinematic viscosity of water are important parameters for many biological or industrial processes.^4–7 The use of computational techniques for various aims (e.g. modelling, simulation, and solving problems) has recently received considerable attention, particularly among researchers in science and engineering. Modelling not only helps develop a comprehensive understanding of a process, but also has the potential to predict and solve problems in specific processes.⁸  Mathematical modelling and computer simulation are also valuable and powerful tools for describing and evaluating their performance under both dynamic and steady-state conditions. On the other hand, there are few systematic articles on the implementation of forecasting models that can be used directly for both design and educational purposes.^9,10  However, to the best of the author’s knowledge, there are no systematic papers specifically devoted to the development of deterministic equations for prediction of the present fluid mechanics-related parameters (e.g. surface tension, specific weight, and kinematic viscosity of water) in the same study. From both engineering and educational perspectives, this work offers a specific computer-based implementation (including nonlinear regression-based analysis, detailed statistical assessment, and special MATLAB^®-based simulations) specifically aimed at exploring explicit formulations for the estimation of these parameters as a function of temperature (i.e. a single input multiple outputs (SIMO)-type modelling study).In consideration of the foregoing facts, the overall objectives of this study were: (i) to derive simple and explicit equations for practicing engineers, researchers, and students, which makes them possible to precisely forecast surface tension, specific weight, and kinematic viscosity of water; (ii) to verify the models’ predictions in terms of several statistical performance indicators; (iii) to evaluate the predictive capabilities of the developed equations by comparing the computer-based outputs with the results from the existed formulations reported in other studies; and (iv) to demonstrate the applicability of the proposed equations on the specific examples in the field of fluid mechanics and hydraulics.

In the present study, a nonlinear regression-based analysis was conducted for the derivation of the temperature-dependent equations [σ_s=f(T), γ_w=f(T), ν_w=f(T)] for surface tension, specific weight, and kinematic viscosity of water at the same time. For this aim, the relevant data sets obtained from the open literature (e.g. several articles, online calculators, and web-based tables) were recorded in Microsoft^® Excel^® Office 365 (Microsoft Inc., Redmond, WA). Thereafter, for the modelling purpose, the data sets were imported from this open database connectivity data source into the DataFit^® (V8.1.69, Oakdale Engineering, PA, US) multiple regression software package running under Windows 10 system on a Casper Excalibur (Intel^® Core^TM i7-7700HQ CPU, 2.81 GHz, 16 GB of RAM, 64-bit) PC. In the nonlinear regression-based analysis, the convergence criteria were implemented for the following values of the solution preferences: (a) regression tolerance=1×10^–10, (b) maximum number of iterations=250, and (c) diverging nonlinear iteration limit=10. When applying the nonlinear regression, the Richardson’s extrapolation method was used to calculate numerical derivatives for the solution of the models. The multiple regression-based analysis was employed based on the Levenberg–Marquardt method with double precision.¹¹  Moreover, the stepwise selection procedure (SSP) was applied as the combination of the forward selection and backward elimination procedures for variable selection process within the framework of DataFit^® software. The SSP begins with a forward step (with no variables in the model). After the forward step, the p-values of the variable coefficients are re-examined, and any insignificant variables are removed in the backward step. This process continues until no variables are either added or removed from the model. The SSP is more generally popular than either the forward or backward procedures.⁹

The models were automatically sorted by the program based on the goodness-of-fit criteria into a graphical interface on the Data Fit^® numeric computing environment. Furthermore, regression variables (β₁, β₂, β₃ for surface tension, δ₁, δ₂, δ₃, δ₄, δ₅, δ₆ for  specific weight, and η₁, η₂, η₃ for kinematic viscosity) and descriptive statistics of the residual errors, such as standard error of the estimate (SEE), sum of residuals (SR), residual average (RA), residual sum of squares (RSS), determination coefficient (R²), correlation coefficient (R), and adjusted coefficient of multiple determination (R_adj²) were also computed to evaluate the performance of the models. Moreover, t-ratios and p-values were also determined for the assessment of the importance of the regression coefficients. An alpha (α) level of 0.05 (or 95% confidence) was used to appraise the statistical significance of the model components.

In the literature, a number of descriptive statistical indicators, such as coefficient of determination (R²), correlation coefficient (R), mean absolute error (MAE), root mean square error (RMSE), systematic and unsystematic RMSE (RMSE_S and RMSE_U, respectively), mean square error (MSE), index of agreement (IA), the factor of two (FA2), fractional variance (FV), proportion of systematic error (PSE), and coefficient of variation (CV), are utilized as helpful mathematical tools to evaluate the prediction performance of any prediction model.¹²  Determination coefficient (R²) denotes that how much of the observed variability is explained for by the prediction model.¹²  Besides, a high value of R implies a significant correlation between the observed data and the predicted values.¹² Additionally, RMSE is one of the most common indicators used with artificial intelligence-based models (e.g. artificial neural networks (ANN), adaptive neuro-fuzzy inference system (ANFIS)) and can be allocated into systematic (RMSE_S) and unsystematic (RMSE_U) components using the least squares fitting. Among them, RMSE_S describes the part of the error due to the model (linear bias). Therefore, a low value implies a good model. RMSE_U describes the part of the error which is due to the random noise and cannot be captured by the model. Moreover, MAE is the simplest of the numerical goodness measures. It is simply the mean of the absolute errors taken over the set of the estimate. Furthermore, PSE is another estimator that gives the ratio of squared systematic and unsystematic errors. Thus, a lower value implies a better model.¹³ Moreover, IA is regarded as a dimensionless relative measure limited in the range of 0–1. Therefore, it is ideal for making cross-comparisons between models. It is a measure of the degree to which model predictions are free of error.¹⁴ FA2 provides the percentage of forecasted cases in which the values of the ratio O/P (observed/predicted) in the range of 0.5–2.0. Furthermore, FV is another normalized measure that allows the comparison of the difference between the predicted variance and the observed variance. A model with FV=0 is a model whose variance is equal to the variance of the observed values.^13,14   In the present study, the proposed formulations were assessed by the above-mentioned statistical indicators to quantify the fit between the source data and the models’ outputs.

The results of the regression analysis revealed that 72 formulations were proposed by the Data Fit^® software for the forecast of the surface tension as a function of temperature. Considering their complexity along with the computed statistics, the model #9 was found sufficiently simple to be used with a hand-held calculator. Likewise, the regression analysis revealed that 47 equations were obtained from the computational analysis for the prediction of the specific weight as a function of temperature. Among them, the model #6 was found to be appropriate to get accurate estimations. Similarly, Data Fit^® software produced 71 regression-based models for the estimation of the kinematic viscosity of water as a function of temperature. From these equations, the model #7 was selected as a simple structure that can be used for the educational purposes. The results of the nonlinear regression analysis yield the final form of the proposed formulations for surface tension (Y₁: σ_s in N/m), specific weight (Y₂: γ_w in kgf/m³), and kinematic viscosity (Y₃: ν_w in m²/s) of water as a function of temperature (X: T in °C). They are presented along with their mathematical forms [Y=f(X)] in Equations (1)–(6) as follows:

$Y_1={\beta }_1+{\beta }_{2}X+{\beta }_3{X}^{1.5}$                                                                                                                             (1)

${\sigma }_s=\frac{7.56}{{10}^2}-\frac{1.21}{{10}^4}T-\frac{4.51}{{10}^6}{T}^{1.5}$                                                                                                                     (2)

$Y_2={\delta }_1{X}^5+{\delta }_2{X}^4+{\delta }_3{X}^3+{\delta }_4{X}^2+{\delta }_{5}X+{\delta }_6$                                                                                            (3)

${\gamma }_w=\frac{2.766}{{10}^9}{T}^5-\frac{8.08}{{10}^7}{T}^4+\frac{9.91}{{10}^5}{T}^3-\frac{9.477}{{10}^3}{T}^2+\frac{7.364}{{10}^2}T+999.845$                                                            (4)

$Y_3=\frac{1}{{\eta }_1+{\eta }_{2}X+{\eta }_3{X}^2}\times {10}^{-6}$                                                                                                                        (5)

${\nu }_w=\frac{1}{0.555+\frac{2.04}{{10}^2}T+\frac{8.914}{{10}^5}{T}^2}\times {10}^{-6}$                                                                                                          (6)

Summary of the regression-based analysis are presented for each model structure in Tables 1–3 (In the tables, SE is the standard error and p-values <0.05 are considered to be significant).It is stated that the larger absolute t-ratio denotes the more significant parameter in the regression model. Moreover, the variable with the lowest p-value can be considered the most significant.^9,10 Based on the absolute t-ratios, the p-values, and standard errors of the model coefficients in Tables 1–3, all models showed very satisfactory performance in estimating surface tension, specific weight, and kinematic viscosity of water. Finally, in order to evaluate the performance of the proposed equations, the computational outputs (models’ predictions) were evaluated by several distinct statistical indicators (e.g. R², R_adj², R, MAE, RMSE, RMSE_S, RMSE_U, PSE, IA, FV, and CV (also called as relative standard deviation, RSD). The results are presented in the next section.

Predictive performances of the proposed nonlinear regression-based models [Y₁: σ_s=f(T), Y₂: γ_w=f(T), Y₃: ν_w=f(T)] are summarized in Table 4. Based the statistical outputs that were determined for each model, it could be inferred that the derived equations exhibited a very satisfactory performance on the estimation of surface tension, specific weight, and kinematic viscosity of water as a function of temperature (R²=0.9999 for all formulations). This result revealed that only 0.01% of the total variations were not described by the proposed equations. Moreover, the large magnitude of the adjusted determination coefficient (R_adj²=0.9999) corroborated the significance of the proposed models.¹²  It is noted that if there are many terms in the model and the sample size is not very large, the R_adj² may be noticeably smaller than the R².¹² For the proposed equations, the R_adj² was determined to be very close to the R² value (almost same), indicating that the compatibility of the sample size used in the present modelling study. Furthermore, very low values of the coefficient of variation (CV=0.0912%, 0.0039%, and 0.4583%, respectively, for surface tension, specific weight, and kinematic viscosity models) demonstrated a high degree of exactitude for the developed formulations, as emphasized in the previous studies.^12–15 As seen from Table 4, other statistical indices also revealed that the present equations yielded very small errors (in terms of MAE, RMSE, RMSE_S, RMSE_U, and PSE) or deviations (according to the closeness to 1 and 0, respectively, for IA and FV) and demonstrated a superior performance on the prediction of the studied fluid mechanics-related parameters (e.g. surface tension, specific weight, and kinematic viscosity of water) as a function of temperature.O, P, m, reg, and i are the subscripts indicating the observed (theoretical), predicted, mean, regression, and index of data points, respectively, σ is the standard deviation, n is the number of data points, p is the total number of explanatory variables in the model (without including the constant term). Finally, Figures 1–3 depict the correlations with best linear equations and corresponding visual agreements between the proposed models and comparative equations. The comparative equations (CE-1 (Equation (7)): σ_s in N/m, CE-2 (Equation (8) and CE-3 (Equation (9): γ_w in kgf/m³, CE-4 (Equation (10) and CE-5 (Equation (11): ν_w in m²/s) obtained from the literature^{4–7, 16–18} are given in Equations (7)–(11). As seen these figures, the proposed surface tension, specific weight, and kinematic viscosity models demonstrated very satisfactory performance (R²=0.9999≈1.0000, p-values <α=0.05) and were comparable with other models.

Figure 1 (A) Relationship between the predicted surface tension values and those obtained from the literature (n=21) and (B) agreement between the literature data and other models (proposed model (Y₁) and comparative equation-1 (CE-1) reported in the literature.^7,16

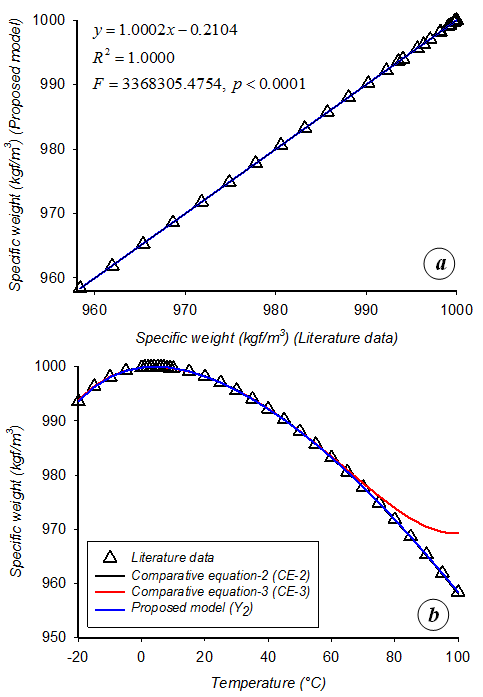
Figure 2 (A) Relationship between the predicted specific weight values and those obtained from the literature (n=33) and (B) agreement between the literature data and other models (proposed model (Y₂), comparative equation-2 (CE-2, Thiesen-Scheel-Diesselhorst equation), and comparative equation-3 (CE-3, Gill’s equation) reported in the literature.^{7, 17}

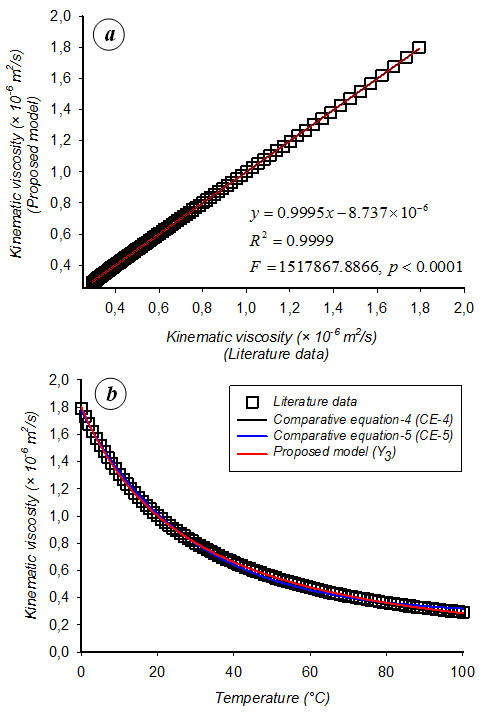
Figure 3 (A) Relationship between the predicted surface tension values and those obtained from the literature (n=101) and (B) agreement between the literature data and other models (proposed model (Y₃), comparative equation-4 (CE-4, Poiseuille’s equation), and comparative equation-5 (CE-5) reported in the literature.^4,7,18

${\sigma }_s=76.0852-(0.1609)[(T+273)-273.15]\times {10}^{-3}$                                                                                        (7)

${\gamma }_w=1000\left(1-\frac{(T+288.9414){(T-3.9863)}^2}{(508929.2)(T+68.1263)}\right)$                                                                                            (8)

${\gamma }_w=999.842594+\frac{6.793952}{{10}^2}T-\frac{9.095290}{{10}^3}{T}^2+\frac{1.001685}{{10}^4}{T}^3-\frac{1.120083}{{10}^6}{T}^4+\frac{6.536332}{{10}^9}{T}^5$                     (9)

${\nu }_w=\frac{0.0179}{1+(0.03368)T+(0.000221)T^2}\times {10}^{-4}$                                                                                              (10)

${\nu }_w=\frac{{\mu }_w}{{\rho }_w}=\frac{\stackrel{{\mu }_w}{\overbrace{0.0002601+0.001517\exp \left\{-0.034688[(T+273.15)-273]\right\}}}}{\left(9.807\frac{N}{kgf}\times \underset{{\rho }_w}{\underbrace{\frac{{\gamma }_w}{g}}}\right)}\times {10}^{-6}$                                            (11)

In this study, predictive performances of the derived nonlinear regression-based models were also compared with other formulations in a numerical manner. For the estimation of the surface tension (σ_s in N/m) data, determination coefficients (R²) were determined as 0.9982 and 0.9999, respectively, for the first comparative equation (CE-1, Equation (7)) ^7,16 and the proposed surface tension model (Equation (2)). The numerical results revealed that the derived formulation given in Equation (2) demonstrated better estimations than the comparative equation-1 (CE-1). Moreover, for the forecast of the specific weight (γ_w in kgf/m³) data, the R² values were computed as 1.0000, 0.9844, and 1.0000, respectively, for the second comparative equation (CE-2, Thiesen-Scheel-Diesselhorst equation, Equation (8)), ^7,17 the third comparative equation (CE-3, Gill’s equation, Equation (9)), ^7,17 and the proposed specific weight model (Equation (4)). In the prediction of the specific weight, the proposed equation (Equation (4)) was determined as successful as the Thiesen-Scheel-Diesselhorst equation (Equation (8)) and showed a better estimation performance than the Gill’s equation (Equation (9)). Furthermore, for the forecast of the kinematic viscosity (ν_w in m²/s) data, the R² values were calculated as 0.9996, 0.9986, and 0.9999, respectively, for the forth comparative equation (CE-4, Poiseuille’s equation, Equation (10)), ^4,7,18  for the fifth comparative equation (CE-5, Equation (11)),^4,7,18 and the proposed kinematic viscosity (Equation (6)). The numerical outputs indicated that the derived formulation given in Equation (6) exhibited better prediction performance compared to the comparative equation-4 (CE-4) and the comparative equation-5 (CE-5). Finally, from the numerical point of view, it is also noted that some useful recent investigations can be found in the field of thermal energy storage,¹⁹ nanofluid flow,^20,21 low-fluid pressure safety valve design,²² heat transfer,²³ and thermal analysis.²⁴

A 0.5-mm-diameter glass capillary tube of uniform bore is dipped vertically in a beaker containing water at 20 °C. Due to surface tension, water rises to a height h in the capillary tube as shown in Figure 4. In atmospheric air, the contact angle of water (and most other organic liquids) with glass is nearly zero, θ≈0°. Determine the capillary rise of water in the tube using the proposed surface tension and specific gravity equations given in Equation (2) and (4), respectively. The horizontal component σ_s∙sinθ acts radially outwards, but vertical component σ_s∙cosθ acts upwards. It is noted that the horizontal component acting all along the circumference of the tube eliminate each other whereas the vertical component balances the weight of water column in the capillary tube. This upward force is responsible for the capillary rise. As the water column is in equilibrium, this force acting upwards is equal to weight of the water column acting downwards. Volume of water in the tube is consisted of a cylindrical water column of height h and water in the meniscus above the plane AB (Figure 4). Thus, volume of cylindrical water column = π∙r²∙h, and volume of water in the meniscus = (volume of cylinder of height r and radius r) – (volume of hemisphere). It is assumed that there are no impurities in the water and no contamination on the surfaces of the glass tube. Also, the experiment is conducted in atmospheric air.

Figure 4 Schematic for Problem 1.

Problem 2

The safe power required for an electric motor rotating a vertical agitator (Figure 5) will be determined based on the following variables: (i) tank volume of 250 m³, (ii) velocity gradient of 5001/s, (iii) temperature of 15 °C, and (iv) safety factor of 1.2 (1 kW=1000 × Watt (W)=1000 × N∙m/s).

Figure 5 Schematic for Problem 2.

MATLAB-based solutions

Problems 1 and 2 were solved by writing scripts (Appendix A1 & A2) in the M-file Editor within the framework of MATLAB^® R2018a software (V9.4.0.813654, 64-bit (win64), Academic License Number: 40578168, Math Works Inc., Natick, MA). The visual representations of the solutions for Problems 1 and 2 are depicted in Figures 6 & 7.

Figure 6 A visual representation of the solution for Problem 1.

Figure 7 A visual representation of the solution for Problem 2.

The present study attempted to address explicit formulations for the estimation of three fundamental fluid mechanics-related parameters (surface tension, specific weight, and kinematic viscosity of water) in the same analysis. Based on the statistical indicators that were calculated in the scope of this work, it was demonstrated that the proposed equations could be safely used for computation of the studied parameters within the proposed limits of the temperature values. It is believed that the derived formulations will be of interest to practising engineers, researchers, and students who are concerned with the relevant problems of the fluid mechanics and hydraulics.

This research has been financially supported by Turkish Academy of Sciences (TÜBA) as a part of Prof. Dr. Kaan Yetilmezsoy’s “The Outstanding Young Scientist Award (TÜBA-GEBİP)” of the year 2018.

There is no conflict of interest declared by the author.

1. Sukhatme SP. A textbook on heat transfer. Hyderabad. Universities Press; 2005.
2. Bahl A, Bahl BS, Tuli GD. Essentials of physical chemistry. Multicolour edition. Ram Nagar S. Chand & Company Ltd; 2009.
3. Hauner IM, Deblais A, Beattie JK, et al. The dynamic surface tension of water. The Journal of Physical Chemistry Letters. 2017;8(7):1599–1603.
4. Yetilmezsoy K, Ilhan F, Kocak E, et al. Feasibility of struvite recovery process for fertilizer industry: A study of financial and economic analysis. Journal of Cleaner Production. 2017;152:88–102.
5. Çengel YA, Cimbala JM. Fluid mechanics fundamentals and applications. New York. McGraw-Hill. 2006.
6. The Physics Factbook. An encyclopedia of scientific essays. Density of water.  
7. Yetilmezsoy K. Composite desirability function-based empirical modeling for packed tower design in physical ammonia absorption. Asia-Pacific Journal of Chemical Engineering. 2012;7(6):795–813.
8. Javadian H, Ghasemi M, Ruiz M, et al. Fuzzy logic modeling of Pb (II) sorption onto mesoporous NiO/ZnCl2-Rosa Canina-L seeds activated carbon nanocomposite prepared by ultrasound-assisted co-precipitation technique. Ultrasonics Sonochemistry. 2018;(40):748–762.
9. Yetilmezsoy K. New explicit equations for estimation of aeration-related parameters in steady-state completely mixed activated sludge process. Global Nest Journal. 2017;19(1):140–159.
10. Yetilmezsoy K. A new simple model for the prediction of waste sludge flow rate in the steady-state completely mixed activated sludge process. Environmental Engineering and Management Journal. 2016;15(12):2613–2630.
11. Yetilmezsoy K. A benchmarking of competing bio-objective functions for multiresponse optimization of UASB system in pretreatment of poultry manure slurry. International Journal for Multiscale Computational Engineering. 2017;15(6):477–504.
12. Yetilmezsoy K, Demirel S, Vanderbei RJ. Response surface modeling of Pb(II) removal from aqueous solution by Pistacia vera L.: Box–Behnken experimental design. Journal of Hazardous Materials. 2009;171(1–3):551–562.
13. Yetilmezsoy K, Abdul-Wahab SA. A prognostic approach based on fuzzy-logic methodology to forecast PM10 levels in Khaldiya residential area, Kuwait. Aerosol and Air Quality Research. 2012;12(6):1217–1236.
14. Ibarra-Berastegi G, Elias A, Barona A, et al. From diagnosis to prognosis for forecasting air pollution using neural networks: Air pollution monitoring in Bilbao. Environmental Modelling & Software. 2008;23(5):622–637.
15. Sen R, Swaminathan T. Response surface modeling and optimization to elucidate and analyze the effects of inoculum age and size on surfactin production. Biochemical Engineering Journal. 2004;21(2):141–148.
16. Liu GB, Yu KT, Yuan XG, et al. Simulations of chemical absorption in pilot-scale and industrial-scale packed columns by computational mass transfer. Chemical Engineering Science. 2006;61(19):6511–6529.
17. Martin JL, McCutcheon SC. Hydrodynamics and transport for water quality modeling. Boca Raton. CRC Press; 1999.
18. Ye WM, Zheng ZJ, Chen B, et al. Effects of pH and temperature on the swelling pressure and hydraulic conductivity of compacted GMZ01 bentonite. Applied Clay Science. 2014;101:192–198.
19. Hoseinzadeh S, Ghasemiasl R, Havaei D, et al. Numerical investigation of rectangular thermal energy storage units with multiple phase change materials. Journal of Molecular Liquids. 2018;271:655–660.
20. Hoseinzadeh S, Otaghsara S, Khatir M, et al. Numerical investigation of thermal pulsating alumina/water nanofluid flow over three different cross-sectional channel. International Journal of Numerical Methods for Heat & Fluid Flow. 2019.
21. Hoseinzadeh S, Heyns P, Kariman H. Numerical investigation of heat transfer of laminar and turbulent pulsating Al2O3/water nanofluid flow. International Journal of Numerical Methods for Heat & Fluid Flow. 2019.
22. Barbaryan T, Hoseinzadeh S, Heyns P, et al. Developing a low-fluid pressure safety valve design through a numerical analysis approach. International Journal of Numerical Methods for Heat & Fluid Flow. 2019.
23. Hoseinzadeh S, Moafi A, Shirkhani A, et al. Numerical validation heat transfer of rectangular cross-section porous fins. Journal of Thermophysics and Heat Transfer. 2019;33;698–704.
24. Hoseinzadeh S, Heyns PS, Chamkha AJ, et al. Thermal analysis of porous fins enclosure with the comparison of analytical and numerical methods. Journal of Thermal Analysis and Calorimetry. 2019;138;727–735.