A random forest (RF) -based decision tree programming methodology was aimed for modeling fully developed turbulent flow conditions in rough pipes. In the present computational study, a flexible RF-based soft-computing strategy was applied for the estimation of the required pipe diameter (D) and Darcy–Weisbach friction factor (λ or f) obtained from the iterative solution of the implicit Colebrook–White equation for five basic pipeline design variables considered in sizing problems (Type 3) of pipe distribution systems. The prediction performance of the implemented RF-based model was assessed more than 15 different statistical goodness-of-fit parameters and useful mathematical diagrams such as box-and-whisker-plots and spread plots. The statistical metrics corroborated the superiority of the RF-based approach in predicting both the required pipe diameter (R² = 0.9793, MAE = 0.0287 m, RMSE = 0.03833 m, SEE = 0.0326 m, IA or WI = 0.9933, CV(RMSE) or SI = 0.0595, NSE = 0.9753, LMI = 0.8482, and AIC = -1954.6438 for the testing dataset) and friction factor (R² = 0.9576, MAE = 0.0011, RMSE = 0.0023, SEE = 0.0018, IA or WI = 0.9851, CV(RMSE) or SI = 0.0660, NSE = 0.9478, LMI = 0.8500, and AIC = -3646.7124 for the testing dataset). The descriptive statics suggested that the 25% percentile values (Q₁), median values (Q₂), and 75% percentile values (Q₃) of RF-predicted values of D and λ and the corresponding actual values of these responses were found to be very close. The proposed RF-based model was also tested against additional some dataset obtained from the relevant literature. The validation results indicated that the applied decision tree-based method produced realistic estimations and acceptable statistics (i.e., R² = 0.9624, MAE = 0.0598 m, and RMSE = 0.0708 m for D values, and R² = 0.9130, MAE = 0.0043, RMSE = 0.0052 for λ values) even at extreme L values greater than 2000 m. This study demonstrated the importance and ability of the applied soft-computing strategy to accurately predict D and λ values and eliminated error-prone steps of the traditional iterative approach.

 Keywords: decision tree-based modeling, friction factor, pipeline design, pipe diameter, random forest, sizing problem, soft-computing, statistical analysis

Computer-aided analysis and design of pipe distribution systems have attracted a great deal of attention from hydraulic engineering researchers in recent years. Three types of problems are typically encountered in the design and analysis of piping systems, covering the use of the Moody diagram or the Colebrook–White equation:^1–6 (1) Type 1 (discharge problem) where the flow rate (Q) is calculated based on known values of pipe length (L), pipe diameter (D), and pressure drop (or head loss (Δh)); (2) Type 2 (head loss problem) where the pressure drop (or head loss, Δh) is calculated based on known values of pipe length (L), pipe diameter (D), and flow rate (Q); and (3) Type 3 (sizing problem) where the pipe diameter (D) is calculated based on known values of pipe length (L), flow rate (Q), and pressure drop (or head loss (Δh)).

The Colebrook–White equation has been widely used to predict the Darcy–Weisbach friction factor λ (sometimes written as f) for turbulent fluid flow in rough pipes.^7,8 Nevertheless, the friction factor already includes this implicit relationship with pipe roughness and Reynolds number (Re). Because the friction factor is a function of the pipe’s relative roughness (ε/D) and Re, the typical design technique necessitates a lengthy iteration procedure even for a single-lined set of pipes and even without accounting for local losses.^2,4 For the problem of Type 1, for instance, this complexity is not an issue because Q can be calculated using a closed-form formulation by calculating $Re\sqrt{\lambda }$ where the velocity V is determined using the Darcy–Weisbach equation and substituted into the right side of the Colebrook–White equation.³ To put it another way, if the minor loss (i.e., one-off losses occurring at a single point) coefficient K is equal to zero, the Darcy–Weisbach equation yields the combination λV², and so λ may be calculated. Knowing both λV² and λ results in V, which then leads to Q.⁹ The Type 2 problem, however, could necessitate repetition. Type 3, on the other hand, is a dimensioning problem and typically requires additional iterative calculations and assumptions to be made in order to achieve convergence.²

In the application of hydraulic engineering, it is impractical to explicitly compute the Re and ε/D because the D is unknown in Type 3 problems.⁶ The simulations are started with a hypothetical pipe diameter value and continued with a fresh one iteratively until convergence for the design issues of such pipe distribution systems. Moreover, the diagram-based technique is sensitive to reading mistakes in the logarithmic scale and is not suitable for computer-aided simulations. These factors suggest that a few attempts to use a descriptive computational technique can make a useful contribution to the practice of hydraulic engineering in designing water distribution networks. In addition to fostering a thorough understanding of a process, modeling offers the power to foresee and address issues in particular systems.¹⁰

Mathematical modeling and computer-aided simulation are also useful and effective approaches to analyze the system performance under complicated and stable situations, as well as to test the present system under different scenarios.^11–13 In the previous research, many data-driven modeling attempts have been made to model various pipelines. For instance, Özger and Yıldırım¹⁴ proposed an adaptive neuro-fuzzy (ANFIS) computing technique to determine the friction coefficient in pipe networks. They tested the performance of the ANFIS-based approach for the commonly used explicit models for the Colebrook-White for a wide range of ε/D (relative roughness) and Reynolds number (Re) values. In another work, Lin et al.¹⁵ developed an integrated method to predict two-phase flow patterns in upward inclined pipes via deep learning neural networks. Additionally, Alhashem and Aramco¹⁶ conducted supervised machine learning as a proof-of-concept in predicting multiphase flow regimes in horizontal pipes. In a different study from Vietnam, Moayedi et al.¹⁷ implemented four machine learning methods (i.e., multilayer perceptron (MLP), M5Rules (M5R), decision table (DT), and trees M5P (TM5P)) for predicting the pressure drop reduction in crude oil pipelines. In a Japanese study conducted by Kobayashi et al.,¹⁸ prediction of drag reduction effect by pulsating turbulent flow was investigated based on machine learning models such as MLP model and long short-term memory (LSTM) model. In another investigation from Canada, Milukow et al.¹⁹ applied gene expression programming (GEP) and extreme learning machines (ELM) for the estimation of the Darcy-Weisbach friction factor for ungauged streams. Moreover, Sattar²⁰ proposed a GEP-based approach to develop new empirical formulas for the prediction of longitudinal dispersion coefficients in pipe flow. Najafzadeh et al.²¹ developed a model tree (MT) to present formulations for evaluation of friction factor in pipes and compared their results with those obtained from GEP, evolutionary paradigm regression (EPR), and conventional models. In another study, Bardestani et al.²² used ANFIS and grid partition method for predicting turbulent flow friction coefficient. Furthermore, Srivastava et al.²³ used artificial neural network (ANN) approach to determine the friction factor for turbulent flows of water in a pipe of uniform circular cross-section.

To the best of the author’s knowledge, there is still a specific literature gap in terms of the application of different soft-computing techniques for estimating the primary parameters in sizing problems (Type 3) of pipe distribution systems, even though the aforementioned investigations have made significant contributions to the field. Previous studies have not yet been directly addressed the random forest (RF)-based decision tree approach for modeling the D and λ within the specified ranges of the main pipeline design variables, such as absolute roughness of the pipe wall (ε), water temperature (T), pipe length (L), flow rate (Q), and head loss (Δh), in the same study. In the traditional approach, D-dependent functions of λ and Re have to be established (e.g., fifth order and vice versa, respectively) to determine the required pipe diameter. In addition, the Re requires the application of the temperature-dependent kinematic viscosity (n). The Colebrook-White equation, on the other hand, combines all D-dependent functions, and D is determined iteratively. Similarly, after determining the diameter D, the friction factor is calculated using the Darcy-Weisbach and continuity equations. All of these are very time-consuming and computationally error-prone processes. However, in the present analysis, D and λ for the specific variables (including ε, T, L, Q, and Δh) were estimated for the first time within the scope of the same study using the RF-based technique. Moreover, kinematic viscosity and a series of iterative calculation steps were eliminated as a result of the suggested soft-computing approach, and a sophisticated predictive modeling scheme was conducted with high precision. Furthermore, the relevant literature has not yet produced a particular RF-based prediction research for the same model variables and their working limitations as the one developed within the context of the current study.

As a consequence, the following objectives have been developed for the current study in order to contribute to addressing the abovementioned gap in this sense: (1) generation of a sufficient amount of fully developed turbulent flow data (including ε, T, L, Q, and Δh) from the iterative solution of the implicit Colebrook–White equation for rough pipes; (2) prediction of D and λ values in the same study utilizing a flexible random forest (RF)-based decision tree technique for sizing problems (Type 3); (3) evaluation of the prediction performance of the established RF-based model using more than 15 different statistical performance evaluations (i.e., R², MAE, RMSE, RMSE_S, RMSE_U, SEE, IA (WI), FV, FA2, CV(RMSE) (SI or NRMSE), NSE, LMI, MFB, MFE, AIC, and U₉₅), box-and-whisker-plots, spread plots, and illustrative/tabulated presentations for the D and λ datasets; (4) validation of the RF-based model’s performance with various turbulent flow data from the open literature; and (5) demonstration of the versatility and adaptability of the implemented soft-computing method for an implicit and trial-and-error type hydraulic engineering problem.

The widely used ensemble machine learning approach known as random forest (RF) creates a structured collection of tree predictors from input vectors by using random vector samples.^24,25 It has shown to be highly effective as a general-purpose classification and regression tool. With a hit-or-miss approach to the procedure, the variables are chosen using the optimal split. The RF method gathers a number of random trees to create random forests. The RF-based approach combines bagging (also known as bootstrap aggregation) and random subspace and functions by merging weak classification trees to get a final result via majority vote. When selecting how to split the forest trees, the number of decision trees to be formed and the number of features to be analyzed to discover the best split must both be considered. Due of the relative efficacy of the RF classifier and the lack of over-fitting, the number of decision trees can be as large as possible. The training data is used to grow each tree by two-thirds. The data from the out-of-bag (OOB) samples, which make up the last third of training samples, can be used to measure performance. As a consequence, the random forest regression is made up of k-trees, where k is the desired number of trees to be produced and can be any value specified by the user. The CART (classification and regression trees) approach is used to grow all of the decision trees in the forest with no pruning. By incorporating numerous criteria, random forest regression allows the tree to grow to the depth of all new training data. A random collection of parameters is chosen as the training set, and a Gini index is utilized to analyze the degree of impurity in the parameters in contrast to the result when generating specific trees.²⁶ The training dataset becomes paramount significance when a single tree splits into just one criterion. Little modifications to the dataset and splitting criterion may result in a range of tree topologies, leading to various interpretations.^24,25 As a result, RF models classify variables based on their importance in order to produce the optimal RF model.

In this study, which was carried out as part of an integrated modeling research, two multiple inputs single output (MISO)-type and RF-based models were established based on a trial-and-error process to evaluate their prediction performances on the required pipe diameter (D) and Darcy–Weisbach friction factor (λ or f) for fully developed turbulent flow conditions in rough pipes. It is noted that the integrated modeling research explores the best-performing data-driven models (e.g., genetic/non-parametric regression/decision tree/kernel/multilayer perceptron/fuzzy logic-based data-intelligent approaches, and so forth) for the estimation of different hydraulic output parameters (e.g., D, f, Re) of the Type-3 problems of pipe distribution systems. Nevertheless, deciding which soft-computing model would be utilized to estimate which output in such scenarios necessitates a thorough optimization research. Therefore, other results (e.g., benchmarking with other state-of-art models) associated with the above-mentioned integrated modeling study will be presented in future studies. Figure 1 shows an original flow network diagram of the proposed RF-based modeling approach applied to estimate D and λ values for the rough flow regime.

Figure 1 Flow network diagram of the RF-based modeling approach that estimates the required pipe diameter (D) and Darcy–Weisbach friction factor (λ) for turbulent water flow in rough pipes.

The purpose of this computer-based investigation was to demonstrate the applicability and usefulness of an RF-based soft-computing technique for estimating both the required pipe diameter (D) and Darcy–Weisbach friction factor (λ) in the sizing problems (Type 3) of pipe distribution systems. In the current work, the implicit Colebrook–White equation was solved using the conventional iteration method for a variety of five significant design parameters, yielding a sufficient number of D and λ datasets (n = 1000 for each of D and λ). The methodology for obtaining fully developed turbulent flow data is in agreement with other studies in the literature.^3,6,22

Absolute roughness of the pipe wall (X₁: ε [=] mm), water temperature (X₂: T [=] °C), pipe length (X₃: L [=] m), flow rate (X₄: Q [=]m³/s), and head loss (X₅: Δh [=] m) were considered as the input variables, whereas the required pipe diameter (Y₁: D [=] m) and Darcy–Weisbach friction factor (Y₂: λ or f [=] dimensionless) were considered as the output variables. As a result, the actual D and λ values were determined from the Colebrook–White equation by simulating the variables indicated above at their working limits. In the present computational study, a flexible RF-based soft-computing strategy was applied for the estimation of D and λ (or f) for the following ranges of five basic pipeline design variables (upper and lower ranges are rounded for simplicity in tracking variable bounds): ε = 0.01–10 mm, T = 5–30 °C, L = 30–2000 m, Q = 0.001–3 m³/s, and Δh = 1–90 m. According to the literature,^27–30 70% of each dataset was used for the model construction (training stage), and 30% of each dataset was utilized for the testing stage.

Table 1 summarizes the detailed descriptive statistics of the simulated variables used in two RF-based and multiple-input single-output (MISO)-type soft-computing models. Because the normalizing technique was not used in this investigation, the inputs contain real units, as seen in Table 1. Many studies analyzed the efficacy of computational analysis utilizing actual (or real) data unit-based and normalized data-based conclusions. Depending on the features of the datasets employed, trials in the current investigation (not provided here due to space constraints) revealed that actual unit-based data outperformed conclusions based on normalized data. This result was shown to be compatible with other earlier soft-computing investigations.^27,31,32

The skewness values showed that absolute roughness of the pipe wall (ε) and pipe length (L) datasets were weakly skewed right, while water temperature (T), flow rate (Q), and head loss (Δh) datasets were weakly skewed left (“-” sign means left-skewed or left-tailed and “+” sign means right-skewed or right-tailed) (Table 1). On the other hand, both the required pipe diameter (D) and Darcy–Weisbach friction factor (λ) datasets had a moderately right-skewed distributions for the numerical outputs generated from the iterative solution of the implicit Colebrook–White equation. In addition, the kurtosis values indicated that all input attributes (ε, T, L, Q, and Δh) had platykurtic distributions (i.e., kurtosis < 3), whereas all output attributes (D and λ) showed leptokurtic nature (i.e., kurtosis > 3). Moreover, scatter plots of the response (or dependent) variables as a function of each explanatory (or independent) variable are illustrated in Figures 2 and 3. Moreover, in accordance with prior MISO-type data-intelligent investigations,^30,33,34 all predictors demonstrated a distinct relevance in accordance with the strength of different types of clusters in particular intervals, indicating that they should not be excluded from the used RF-based model.

Figure 2 Scatter plots of D and λ as a function of the first three predictor variables (ε, T, L).

In the present analysis, the RF-based soft-computing model was established within the numerical computing environment of WEKA 3.9.6 (Waikato Environment for Knowledge Analysis) software (The University of Waikato, Hamilton, New Zealand, https://www.cs.waikato.ac.nz/ml/weka/). In order to assess the efficacy and usefulness of the RF-based model using D and λ datasets produced under fully developed turbulent flow conditions in rough pipes, WEKA Explorer was used as a potent data mining tool. It is worth noting that randomization, also known as data shuffling, is a common technique to overcome this issue since learning algorithms may be sensitive to the sequence in which the data is acquired. For this reason, the randomization procedure was employed using WEKA’s “randomize” filter (package weka.filters.unsupervised.instance.randomize) before dividing the original datasets (diameter_ALL.arff and friction_ALL.arff), each with 5 inputs and 1 output, into the training and testing datasets. It is noted that the xlsx data files (Microsoft^® Excel^® standard format file type) were converted to the csv (comma-separated values) and txt (a standard text document (e.g., Microsoft^® Notepad) that contains plain text) files, respectively, and finally converted to the arff (attribute-relation file format) files for reading datasets in WEKA. To guarantee uniformity and repeatability, D and λ datasets were shuffled using a random seed value of 42, which is in line with prior studies.^35–37The full randomized datasets (diameter_ALL_random.arff and friction_ALL_random.arff) were then separated into training and testing datasets (herein these datasets are abbreviated as TRA and TES, respectively) using the “remove percentage” filter option in WEKA (located in package weka.filters.unsupervised.instance.removepercentage) Following that, these datasets were saved as diameter_random_TRA.arff and friction_random_TRA.arff for the training stages and diameter_random_TES.arff and friction_random_TES.arff for the testing stages of the computational analysis. The block diagram/working process of WEKA Java-based open-source machine learning platform machine learning software (released under GNU General Public License (GNU GPL)) can be observed in a recent MLP-based research undertaken by Sharma et al.³⁸

In this computational study, various distinct statistical performance metrics (i.e., R², b (slope), a (intercept), MAE, RMSE, RMSE_S, RMSE_U, SEE, IA (WI), FV, FA2, CV(RMSE) (SI or NRMSE), NSE, LMI, MFB, MFE, AIC, and U₉₅, and so forth) were computed by executing a new solution script (statistics.m) written in the M-file Editor within the framework of MATLAB^® R2018a software (V9.4.0.813654, 64-bit (win64), Academic License Number: 40578168, MathWorks Inc., Natick, MA) running under Windows 10 system on the same PC platform. Full descriptions and formulations of the respective evaluators are presented in the following section.

The following assumptions were employed in this soft-computing investigation on fully developed turbulent flow conditions in sizing problems (Type 3):

(1) Pipe was considered to be totally filled with water in the internal flow,

(2) Piping system as a whole has a constant diameter (D), and the total head loss (Δh) is calculated from,

(3) Minor (local) losses’ impact was not taken into account (K = 0) (this will be covered in the upcoming research), and hence the Darcy–Weisbach equation yielded the Δh as a function of λ, D, V, g, where g = 9.807 m/s²,

(4) According to the continuity equation, Q was considered as constant and obtained by ,$Q=VA=V\left(\left(\pi D^2\right)/4\right)$

(5) Because commercial pipes are only manufactured with particular standard sizes in practice, the next diameter available will be selected based on the computed or predicted value of D.

(6) The importance of each independent variable was assumed to be equal, and no special safety measures were taken when building the model to prevent any knowledge bias,

(7) Yetilmezsoy’s empirical formula^6,13,39,40 was used to calculate the kinematic viscosity (ν [=] m²/s) as a function of temperature (valid for T = 0–100 °C),

(8) Yetilmezsoy’s fifth order nonlinear regression-based equation^6,13,39 was used to calculate the specific weight (γ [=] kgf/m³) as a function of temperature (valid for T = -20–100 °C),

As part of the current computational analysis, numerous significant statistics, such as slope of the best-fit line (b), intercept (a), determination coefficient (R²), mean absolute error (MAE), root mean squared error (RMSE), systematic and unsystematic RMSE (RMSE_S and RMSE_U, respectively), standard error of the estimate (SEE), index of agreement (IA) (or known as Willmott’s Index (WI)), fractional variance (FV), the factor of two (FA2), coefficient of variation of RMSE (CV(RMSE) (or known as scattering index (SI) or normalized root mean squared error (NRMSE)), Nash–Sutcliffe efficiency (NSE), Legates and McCabe’s index (LMI), mean fractional bias (MFB), mean fractional error (MFE), Akaike information criterion (AIC) (named after the Japanese statistician Hirotsugu Akaike), and expanded uncertainty with 95% confidence level (U₉₅) were calculated to measure the agreement and make comparisons between the observed values and predictions of the used RF-based technique for the training and testing datasets. The mathematical formulations of the computed performance metrics are provided in Equations (1) to (21). In these expressions, the letters O, P, m, n, reg, and i denote the observed, predicted, mean, number of data points (in both training and testing datasets), regression, and index of data points, respectively. In Equations (10)–(13), the Greek letter σ refers to the standard deviation. In Equations (14) and (15), RSE and RAE are the abbreviations of the relative squared error and the relative absolute error, respectively. In Equation (18), “ln” is the natural logarithm, and k_e is the number of parameters being estimated.

Comprehensive explanations of these measurements (which are not included here owing to space constraints) may be found in prior research including soft-computing-based modeling of the flow rate of dry part in the wet gas mixture,²⁹ approximation of the discharge coefficient of differential pressure flowmeters,²⁸ modeling of the lateral confinement coefficient for carbon fiber reinforced polymer (CFRP)-confined rectangular/square reinforced concrete columns,²⁷ group method of data handling (GMDH)-extreme learning machine (ELM)-based prediction of longitudinal dispersion coefficients in water pipelines,⁴¹ weather research and forecasting (WRF)-community multiscale air quality (CMAQ)-based modeling of meteorological parameters and PM_2.5 concentrations,⁴² performance evaluation of solar radiation computing models,⁴³ assessment of the precision of mathematical models,⁴⁴ resistant MAPE (R-MAPE)-based statistical assessment of prediction accuracy,⁴⁵ intercomparison of wind speed probability distribution models,⁴⁶ prediction of daily global solar radiation from sunshine duration,⁴⁷ estimation of discharge capacity of sharp-crested weirs,⁴⁸ and empirical modeling of pipe-sizing problems.⁶

In order to get the optimum user-defined parameter values, decision tree-based model implementation takes some trial and error.²⁹ As a result, in order to obtain better model prediction or minimize error, the values for each parameter in the RF model must be effectively adjusted.⁴⁹ The user-defined parameter values were optimized for the following parameters in the current study utilizing a number of RF-based model trials: (a) bag size percent (size of each bag as a percentage of the training set size) = 100, (b) batch size (preferred number of instances to process if batch prediction is being performed) = 100, (c) the maximum depth of tree = 0 (0 is used for unlimited), (d) number of execution slots (number of threads to use for constructing the ensemble) = 1, (e) number of features (number of randomly chosen attributes) = 0 (if 0, int(log_2(#predictors) + 1) function is used per split in each tree), (f) number of iterations (number of tress in the RF) = 100, and (g) random number seed to be used = 1. The values obtained in the earlier decision tree-based modeling research^49,50 are consistent with these settings.

The elapsed time during the computational analysis is one of WEKA’s output parameters. For the present pipe diameter (D) dataset, the time records for the building, training, and testing of the RF-based model were 0.28 seconds for 700 instances, 0.31 seconds for 700 instances, and 0.14 seconds for 300 instances, respectively. At the end of the analysis carried out in WEKA, RF-based predictions on the training set of D (n = 700) produced a correlation coefficient (R) of 0.9985, a mean absolute error (MAE) of 0.0117 m, and root mean squared error (RMSE) of 0.0168 m, while R, MAE, and RMSE values for the testing set of D (n = 300) were computed as 0.9896, 0.0287 m, and 0.0383 m, respectively. Likewise, for the current Darcy–Weisbach friction factor (λ) dataset, the time records for the building, training, and testing of the RF-based model were 0.17 seconds for 700 instances, 0.28 seconds for 700 instances, and 0.11 seconds for 300 instances, respectively. The computational results showed that the RF-based estimations on the training set of λ (n = 700) yielded an R value of 0.9971, an MAE of 0.0005, and an RMSE value of 0.0009 m, while R, MAE, and RMSE values for the testing set of λ (n = 300) were determined as 0.9789, 0.0011, and 0.0023, respectively.

As seen from the statistics summarized in Table 2, R² values were determined as 0.9793 and 0.9576 for testing sets of D and λ, revealing that the RF-based approach satisfactorily predicted the expected responses (D and λ) with small deviations for each subset. The R² values indicated that unexplained variations were only 2.07% and 4.24% of all the variations in prediction of the pipe diameter and Darcy–Weisbach friction factor, respectively. The calculated IA (0.9990 and 0.9933) and FA2 (0.9936 and 0.9816) values (for the training and testing datasets of D, respectively) were determined to be very close to 1, implying that very satisfactory agreements were achieved between the actual and RF-predicted D values. In addition, IA (0.9978 and 0.9851) and FA2 (0.9975 and 1.0011) values (for the training and testing datasets of λ, respectively) values corroborated that acceptable agreements were attained between the actual and RF-predicted λ values.

The low values of the CV(RMSE) ((a) 0.0254 and 0.0595 for the training and testing datasets of D, respectively; and (b) 0.0268 and 0.0660 for the training and testing datasets of λ, respectively) showed a high degree of precision and a good deal of the reliability of the proposed RF-based method. Moreover, AIC values of the RF-based model were fairly low in all subsets, indicating the accuracy of the RF-based decision tree strategy applied to estimate the D and λ values. Other descriptive performance metrics, such as MAE, RMSE (including its systematic and unsystematic components), FV, MFB, MFE, and U₉₅, also revealed that the proposed soft-computing model produced very small residuals/uncertainty and demonstrated a noticeable predictive performance in estimating the required pipe diameter (D) and Darcy–Weisbach friction factor (λ).

Figures 4 and 5 show the linear correlation between the actual and forecasted values of the actual and RF-predicted values of D and λ for both training and testing phases, respectively. As seen from Figure 4, predicted D values obtained by the RF-based approach range within the ±10% error band during the training stage and within the ±22% error band during the testing stage. Similarly, Figure 5 shows that λ values estimated by the RF-based model range within the ±15% error band during the training stage and within the ±25% error band during the testing stage.

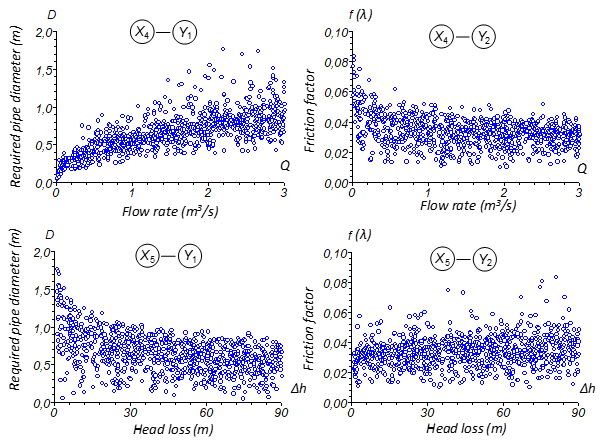
Figure 3 Scatter plots of D and λ as a function of the fourth and fifth predictor variables (Q, Δh).

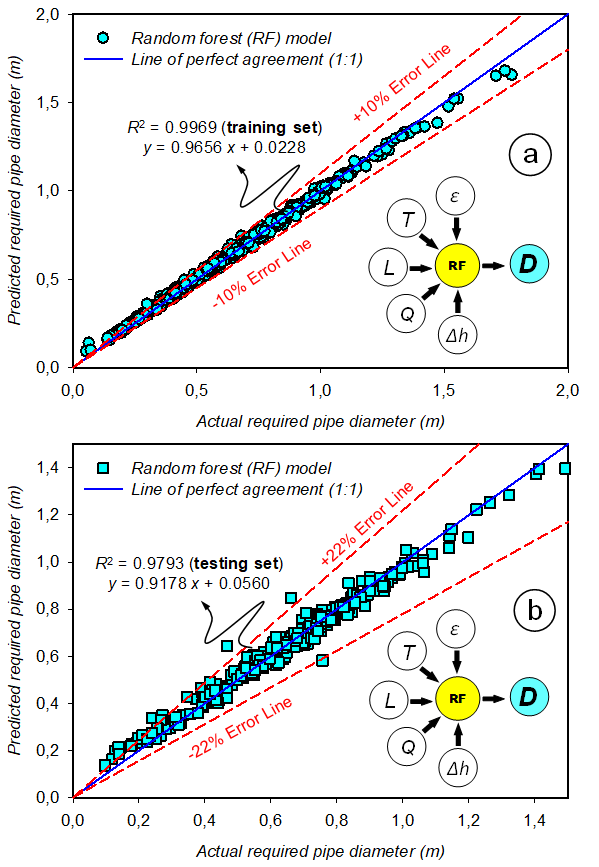
Figure 4 Linear correlation between the actual and RF-predicted values of pipe diameter (D): (a) training stage (n = 700) and (b) testing stage (n = 300).

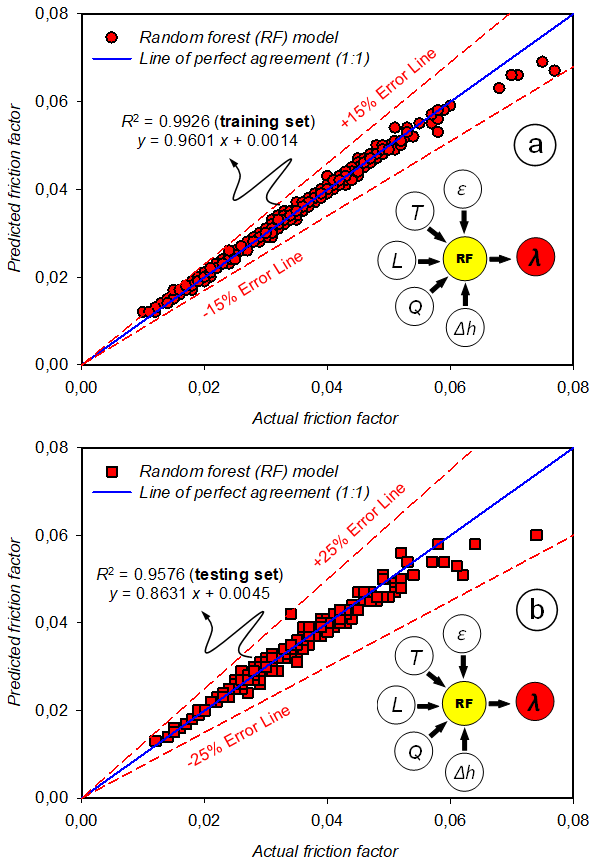
Figure 5 Linear correlation between the actual and RF-predicted values of Darcy–Weisbach friction factor (λ or f): (a) training stage (n = 700) and (b) testing stage (n = 300).

Furthermore, in terms of visual comparisons, the prediction accuracy of the applied soft-computing strategy was evaluated using two useful graphical methods such as box-and-whisker plot and spread plot. The box-and-whisker plots summarize each variable by the following components as follows:^6,30 (1) the median value (Q₂: median or second quartile) in each box acts as a center solid line to represent the location or central tendency; (2) a box represents the range of variation around this central tendency (the edges of the box are the 25th (Q₁: lower quartile or first quartile) and 75th (Q₃: upper quartile or third quartile) percentiles); and (3) the error range (Q₄-Q₀: maximum value - minimum value) is displayed as whiskers around the box. It is noted that black diamond (♦) inside each boxplot represents the mean value. Moreover, the spread plot is a useful way to display the distribution of data across groups. It provides a fully graphical picture of the spread of the data. The vertical axis is divided into any number of divisions that correspond to the width of a plot point. If more than one data point falls within a division, they are shown alongside the first. As a result, a broad band represents a concentration of data at a specific value.

Figures 6 and 7 illustrate box-and-whisker and spread plots of the actual datasets against the RF-based estimations for the prediction of the required pipe diameter (D) and Darcy–Weisbach friction factor (λ or f), respectively. On basis of the training and testing datasets of D and λ (or f), shapes of both box-and-whisker and spread plots of the RF-based decision tree approach appear almost similar to the actual values of the respective responses.

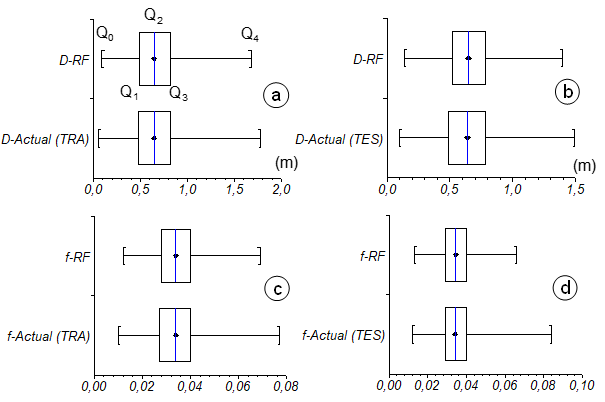
Figure 6 Box-and-whisker plots of the actual and RF-predicted values of D and f (or λ) datasets: (a) training stage (n = 700) and (b) testing stage (n = 300).

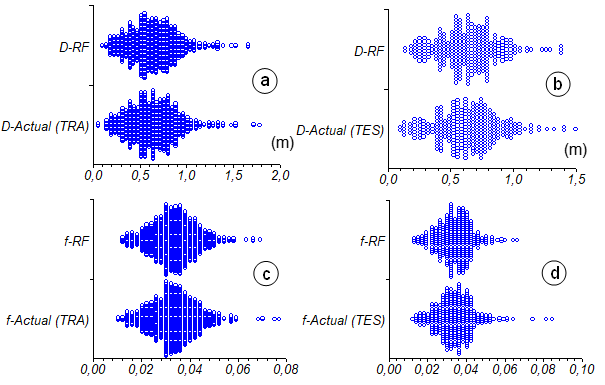
Figure 7 Spread plots of the actual and RF-predicted values of D and f (or λ) datasets: (a) training stage (n = 700) and (b) testing stage (n = 300).

 In order to examine the consistency of the RF-based estimations over the actual values, the 25%, 50%, and 75% quartile values of D and λ datasets are presented in Tables 3 and 4, respectively. When both Figure 6 (box-and-whisker plots) and Tables 3 and 4 are scrutinized, the descriptive statics suggest that the 25% percentile quartile values (Q₁), median 50% percentile values (Q₂), and 75% percentile quartile values (Q₃) of RF-estimated D and λ datasets are very close to their the corresponding actual values. As seen from Tables 3 and 4, the interquartile ranges (IQR) of and RF-predicted values and the respective actual values of D and λ are quite close to each other.

Finally, validation datasets were built for both output variables using open literature data to check the prediction performance of the RF-based model on D and λ values (Table 5). Descriptions of pipe material acronyms are presented below the table. Figure 8 depicts the agreements between the observed values and the RF-based model predictions for the D and λ validation datasets.

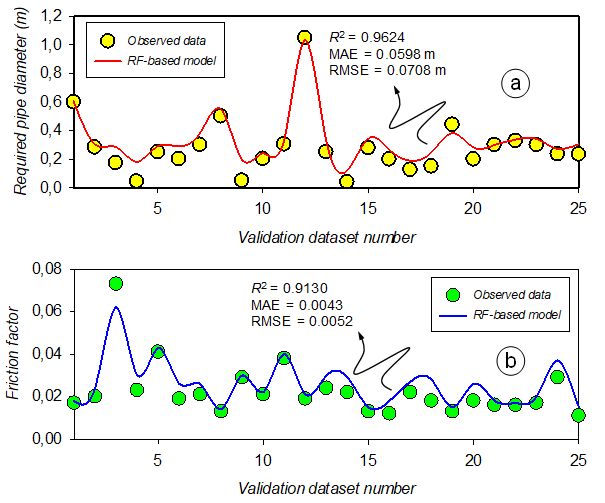
Figure 8 Agreement between the observed values and the RF-based model outputs for the validation datasets of D and λ.

Statistical measurements for the validation datasets of D and λ were obtained as follows, in their respective order: R² = 0.9624 and 0.9130; MAE = 0.0598 m and 0.0043; RMSE = 0.0708 m and 0.0052; RMSE_S = 0.0621 m and 0.0042; RMSE_U = 0.0339 m and 0.0031; SEE = 0.0353 m and 0.0033; IA = 0.9653 and 0.9499; FV = 0.1469 and 0.1677; and AIC = -130.4128 and -260.5149. Notwithstanding the fact that the pipe length dataset contains some extreme values (i.e., L > L_max » 2000 m) in comparison to the present modeling constraints (Table 1), the statistical findings indicated the validity of the RF-based decision tree strategy implemented to estimate the D and λ values.

An RF-based soft-computing approach was implemented for the first time in the estimation of the required pipe diameter (D) and Darcy–Weisbach friction factor (λ or f) in the same study. In the present computational analysis, five primary pipeline design components (ε, T, L, Q, Δh) were simulated for fully developed turbulent flow conditions in sizing problems (Type 3) of rough pipes. The results were analyzed in terms of various statistical performance measures and useful mathematical diagrams.

It was shown that, in contrast to traditional computing, the suggested RF-based strategy offered a well-flexible solution for calculating both D and λ values, not worse than the old labor-intensive methods. It should be emphasized that the present computational study was carried out as a part of an integrated modeling research exploring the prediction performance of various soft-computing methodologies on the estimation of different hydraulic outputs (e.g., D, λ, Re) for Type 3 problems of pipe distribution systems. This study demonstrated the efficacy of an RF-based data-intelligent model without the need for the cumbersome and time-consuming steps of the traditional iterative technique (trial-and-error progress). Any data collection with missing values may be avoided by using the soft-computing technique that is being used. In this regard, the approach for calculating both D and λ values offers a fairly flexible strategy.

According to the results, the suggested RF-based decision tree technique produced quantitative predictions in a computation time of just a few seconds. As a consequence, the established method provided a speedy solution to pipeline sizing problems within the studied limitations of the relevant input data. It should be underlined that while all efforts in this field are valued as a product of labor, there is always a demand for high-performance and adaptable approaches for hydraulic engineering applications. From this stand point, it would be worthwhile to expand the existing research to more fully characterize the behavior of turbulent flow conditions using a number of sophisticated hybrid techniques. Furthermore, additional effort is recommended to build novel soft-computing models that take into account the influence of varied minor (local) loss coefficients (K). It was concluded that the flexibility of the proposed strategy will make it an appropriate data-driven tool for modeling of other highly iterative hydraulic engineering applications

The author would like to thank Ms. Regina Cooper (Editorial & Review Analyst from MedCrave Group) who provided encouragement and time support during the creation of this work.

The author declares that he has no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

1. Hoeft C, Irwin B, Urroz G, et al. Engineering Field Handbook, Chap 3 (650.03) Hydraulics, Fort Worth, Texas, USA. 2009.
2. Yıldırım G, Singh VP. A MathCAD procedure for commercial pipeline hydraulic design considering local energy losses. Adv Eng Software. 2014;41(3):489–496.
3. Babajimopoulos C, Terzidis G. Accurate explicit equations for the determination of pipe diameters. Int J Hydraulic Eng. 2013;2(5):115–120.
4. Çengel YA, Cimbala JM. Fluid mechanics fundamentals and applications. New York. McGraw-Hill. 2014.
5. Medina YC, Fonticiella OM, Morales OF. Design and modelation of piping systems by means of use friction factor in the transition turbulent zone. Mathematical Modelling of Engineering Problems. 2017;4(4):162–167.
6. Yetilmezsoy K, Bahramian M, Kıyan E, et al. Development of a new practical formula for pipe-sizing problems within the framework of a hybrid computational strategy. J Irrigation Drainage Eng. 2021;147(5):04021012.
7. Colebrook CF, White CM. Experiments with fluid friction in roughened pipes. Proceedings of the Royal Society of London. Series A-Mathematical and Physical Sciences. 1937;161(906):367–381.
8. Colebrook CF. Turbulent flow in pipes, with particular reference to the transition region between the smooth and rough pipe laws. Journal of the Institution of Civil Engineers. 1939;11(4):133–156.
9. Apsley D. Lecture Notes, Hydraulics 2, Topic T2: Flow in Pipes and Channels, Department of Mechanical, Aerospace and Civil Engineering. The University of Manchester, Manchester, UK. 2013.
10. Murillo A, Taormina R, Tippenhauer NO, et al. High-fidelity cyber and physical simulation of water distribution systems. I: Models and data. J Water Res Planning Management. 2023;149(5):04023009.
11. Abokifa AA, Sela L (2023). Integrating spatial clustering with predictive modeling of pipe failures in water distribution systems. Urban Water Journal. 2023;20(4):465–476.
12. Park H, Kim K, Hyung J, et al. Decision-making for the hazard ranking of water distribution networks using the TOPSIS method. Water Supply. 2023;23(2):715–726.
13. Yetilmezsoy K. Introduction of explicit equations for the estimation of surface tension, specific weight, and kinematic viscosity of water as a function of temperature. Fluid Mech Res Int J . 2020;4(1):7–13.
14. Özger M, Yıldırım G. Determining turbulent flow friction coefficient using adaptive neuro-fuzzy computing technique. Adv Eng Software. 2009:40(4):281–287.
15. Lin Z, Liu X, Lao L, et al. Prediction of two-phase flow patterns in upward inclined pipes via deep learning. Energy. 2020;210:118541.
16. Alhashem M, Aramco S. Supervised machine learning in predicting multiphase flow regimes in horizontal pipes. Abu Dhabi International Petroleum Exhibition & Conference, Society of Petroleum Engineers, Abu Dhabi. 2019.
17. Moayedi H, Foong LK, Nguyen H. Soft computing method for predicting pressure drop reduction in crude oil pipelines based on machine learning methods. J Braz Soc Mech Sci Eng. 2020;42:1–11:562.
18. Kobayashi W, Shimura T, Mitsuishi A, et al. Prediction of the drag reduction effect of pulsating pipe flow based on machine learning. Int J Heat Fluid Flow. 2021;88:108783.
19. Milukow HA, Binns AD, Adamowski J, et al. Estimation of the Darcy–Weisbach friction factor for ungauged streams using gene expression programming and extreme learning machines. J Hydrol. 2019;568(11):311–321.
20. Sattar AM. Gene expression models for the prediction of longitudinal dispersion coefficients in transitional and turbulent pipe flow. J Pipeline Syst Eng Practice. 2014;5(1):04013011.
21. Najafzadeh M, Shiri J, Sadeghi G, et al. Prediction of the friction factor in pipes using model tree. ISH J Hydraulic Eng. 2018;24(1):9–15.
22. Bardestani S, Givehchi M, Younesi E, Sajjadi S, Shamshirband S, Petkovic D. Predicting turbulent flow friction coefficient using ANFIS technique. Signal, Image and Video Processing. 2017;11(2):341–347.
23. Srivastava V, Prakash A, Rawat A. To predict frictional pressure-drop of turbulent flow of water through a uniform cross-section pipe using an artificial neural network. Tadepalli, T, Narayanamurthy, V. (eds) Recent Advances in Applied Mechanics. Lecture Notes in Mechanical Engineering. Springer, Singapore, 2022.
24. Breiman L. Bagging predictors. Machine Learning. 1996;24:123–140.
25. Breiman L. Random Forests. Machine Learning. 2001;45:5–32
26. Breiman L, Friedman J, Olshen, R, et al. Classification and regression trees. Chapman and Hall/CRC, Boca Raton, FL, USA, 1984:368.
27. Yetilmezsoy K, Sihag P, Kıyan E, et al. A benchmark comparison and optimization of Gaussian process regression, support vector machines, and M5P tree model in approximation of the lateral confinement coefficient for CFRP-wrapped rectangular/square RC columns. Engineering Structures. 2021;246:113106.
28. Dayev Z, Kairakbaev A, Yetilmezsoy K, et al. Approximation of the discharge coefficient of differential pressure flowmeters using different soft computing strategies. Flow Measurement and Instrumentation. 2021;79:101913.
29. Dayev Z, Shopanova G, Toksanbaeva B, et al. Modeling the flow rate of dry part in the wet gas mixture using decision tree/kernel/non-parametric regression-based soft-computing techniques. Flow Measurement and Instrumentation. 2022;86:102195.
30. Dayev Z, Yetilmezsoy K, Sihag P, et al. Modeling of the mass flow rate of natural gas flow stream using genetic/decision tree/kernel-based data-intelligent approaches. Flow Measurement and Instrumentation. 2023;90:102331.
31. Thakur MS, Pandhiani SM, Kashyap V, et al. Predicting bond strength of FRP bars in concrete using soft computing techniques. Arabian Journal for Science and Engineering. 2021;46(5):4951–4969.
32. Yaseen ZM, Sihag P, Yusuf B, Al‐Janabi AMS. Modelling infiltration rates in permeable stormwater channels using soft computing techniques. Irrigation and Drainage. 2020;70(1):117–30.
33. Yetilmezsoy K, Karakaya K, Bahramian M, et al. Black-, gray-, and white-box modeling of biogas production rate from a real-scale anaerobic sludge digestion system in a biological and advanced biological treatment plant. Neural Computing and Applications. 2021;33(17):11043–11066.
34. Yetilmezsoy K, Abdul-Wahab SA. A prognostic approach based on fuzzy-logic methodology to forecast PM10 levels in Khaldiya residential area, Kuwait. Aerosol and Air Quality Research. 2012;12(6):1217–1236.
35. Hassan D, Hussein, HI, Hassan, MM. Heart disease prediction based on pre-trained deep neural networks combined with principal component analysis. Biomedical Signal Processing and Control. 2022;79:104019.
36. Coban O. Use of different variants of item response theory-based feature selection method for text categorization. In: 2022 International Conference on Theoretical and Applied Computer Science and Engineering (ICTASCE), Ankara, Turkey, 2022:66–71.
37. Wang Y, Cui W, Vuong NK, et al. Feature selection and domain adaptation for cross-machine product quality prediction. J Intelligent Manufacturing. 2023;34:1573–1584.
38. Sharma K, Derlon N, Hu S, et al. Modeling the pH effect on sulfidogenesis in anaerobic sewer biofilm. Water Res. 2014;49:175–185.
39. Yetilmezsoy K, Ilhan F, Kiyan E, et al. A comprehensive techno-economic analysis of income-generating sources on the conversion of real sheep slaughterhouse waste stream into valorized by-products. J Environ Manag. 2022;306:114464.
40. Gross M, Karbasi B, Reiners, T, et al. Implementing prosumers into heating networks. Energy. 2021;230:120844.
41. Saberi-Movahed F, Najafzadeh M, Mehrpooya A. Receiving more accurate predictions for longitudinal dispersion coefficients in water pipelines: training group method of data handling using extreme learning machine conceptions. Water Res Manag. 2020;34(2): 529–561.
42. Wang Q, Luo K, Fan J, et al. Spatial distribution and multiscale transport characteristics of PM2.5 in China. Aerosol and Air Quality Res. 2019;19(9):1993–2007.
43. Badescu V. Assessing the performance of solar radiation computing models and model selection procedures. Journal of Atmospheric and Solar-Terrestrial Physics. 2013;105:119–134.
44. Caliskan N, Jadraque E, Tham Y, Muneer T. Evaluation of the accuracy of mathematical models through use of multiple metrics. Sustainable Cities and Society. 2011;1(2):63–66.
45. Moreno JJM, Pol AP, Abad AS, et al. Using the R-MAPE index as a resistant measure of forecast accuracy. Psicothema. 2013;25(4):500–506.
46. Çelik AN, Makkawi A, Muneer T. Critical evaluation of wind speed frequency distribution functions. Journal of Renewable and Sustainable Energy. 2010;2(1):013102.
47. Fan J, Wu L, Zhang F, et al. Empirical and machine learning models for predicting daily global solar radiation from sunshine duration: A review and case study in China. Renewable and Sustainable Energy Reviews. 2019;100:186–212.
48. Shabanlou S. Improvement of extreme learning machine using self-adaptive evolutionary algorithm for estimating discharge capacity of sharp-crested weirs located on the end of circular channels. Flow Measurement and Instrumentation. 2017;59:63–71.
49. Sharafati A, Khosravi K, Khosravinia P, et al. The potential of novel data mining models for global solar radiation prediction. International Journal of Environmental Science and Technology. 2019;16(11):7147–7164.
50. Nwulu NI. Modelling locational marginal prices using decision trees. International Conference on Information and Communication Technologies (ICICT), Karachi, Pakistan. 2017:156–159.
51. Schumack M. Solution of complex pipe flow problems using spreadsheets in an introductory fluid mechanics course, In: Proceedings of the 2004 American Society for Engineering Education Annual Conference & Exposition, Session 3666. 2004:1–13.
52. Senturk A. Hydraulics, Pipe Flow, Department of Civil Engineering, Istanbul Kültür University, Turkey. 2009.
53. Subramanian RS. Pipe Flow Calculations, Department of Chemical and Biomolecular Engineering, Clarkson University, Clarkson, New York, USA. 2011.
54. Ghabayen SMS, Abualtayef M. Hydraulics - ECIV 3322, Chapter 3: Water Flow in Pipes, Civil Engineering Department, The Islamic University of Gaza Faculty of Engineering, Gaza, Palestine. 2012:1–110.
55. Sakkas JG. Generalized numerical and nomographic solutions of simple pipe flow problems. Water Utility Journal. 2014;7:51–64.
56. Siddique M. Fluid Mechanics, Losses in Pipes Dynamics of Viscous Flows. Sharjah, UAE. 2015.
57. Ergil M. Teaching, CIVL332 – Hydromecanics, Lecture Notes, Frictional Losses in Completely Developed Pressurized Pipe Flowing Full, Eastern Mediterranean University, Turkish Republic of Northern Cyprus. 2020:1–69.
58. Almoulki T, Yetilmezsoy K. MATLAB for Iteration: Hydraulic modeling for environmental engineering students. Fluid Mech Res Int. 2019;3(1):24–28.