In this study, steady, three dimensional, laminar stagnation point flow and heat transfer of a non-Newtonian Reiner-Rivlin fluid due to a radially stretchable rotating disk has been investigated for the first time. Analytical solutions of the governing coupled, nonlinear, ordinary differential equations, deduced directly from the Naveir-Stokes equations by means of similarity transformations, are obtained using a highly effective analytical method, called, Homotopy Analysis Method (HAM). A comparison of HAM results with Homotopy Perturbation Method (HPM) is also performed to show the efficiency of HAM over HPM. It has been observed that, increasing stretching in general decreases the magnitude of azimuthal, axial component of velocity and temperature distributions, while the radial component increases near the surface of the disk for small stretching followed by a continuous decrease for large stretching. Also, the radial and tangential stresses are found to be decreasing functions of the stretching parameter.

Keywords: Stagnation flow Stretchable disk HAM Reiner-Rivlin fluid Rotating disk.

 In general, it is always difficult to find exact solution of the Navier-Stokes equations, primarily because of their non-linearity. The planner two dimensional stagnation point flow, initially solved by¹ and axisymmetric three dimensional stagnation point flow by^2,3 are a few of the problems in fluid dynamics which admit exact solution of the Navier-Stokes equations. The stagnation point flow represents the fluid flow in the immediate neighborhood of solid surface at which fluid approaching the surface divides into different streams and it is evident from literature that stagnation flows are studied extensively because of their importance in both theory and practice. From a practical point of view, these flows have applications in forced convection cooling processes where a coolant is impinged on a flat plate. The classical Karman⁴ problem is another example of an exact solution of the Navier-Stokes equations. In his paper, Karman showed that, the steady, viscous flow around a single disk rotating in an initially stationary fluid is an exact solution of the Navier-Stokes equations reducing the governing system of partial differential equations into a set of ordinary differential equations using the similarity variables which are now known as Karman similarity variables. The subject of flows associated with rotating disks occupies a key position in the field of fluid mechanics because of their immense practical importance. Rotating-disk systems can be used to model the flow and heat transfer associated with the internal-air systems of gas turbines, where disks rotate close to a rotating and stationary surface. In addition, rotating-disk systems are used in electro-chemistry (rotating-disk electrodes), bio and chemical reactors, transport engineering (automobile brakes), rotating-disk cleaners, etc. Hence, after Karman’s⁴ seminal work, considerable attention has been given to the extensions of his problem, such as, the effects of suction,⁵ of partial slip,⁶ of stretching,⁷ of forced convection⁸ and many more.

Present study focuses on another important extension of this problem which is the stagnation point flow over a rotating disk, which has long been a subject of investigations. This phenomenon commonly occurs in many engineering and industrial applications such as wastewater treatment, rotating machinery, medical equipment, rotating blades, computer storage devices etc. Moreover, forced flow due to a rotating disk occurs on all blunt rotating bodies moving in a fluid and thus present analysis meets the identified need to evaluate the exact analytical solution of a practical problem. Hannah⁹ was the first to analyze the flow fields arising from a laminar forced flow impinging on a rotating disk. He obtained an approximate series solution of velocity profiles near the disk surface. Schlichting et al.,¹⁰ gave another series solution of velocity components using an integral method. The steady heat transfer in this flow has been investigated by Tien et al.,¹¹ using the velocity functions of Hannah’s⁹ result. A more general problem of boundary-layer transfer over a rotating axisymmetric bodies, including rotating disk as a special case has been studied by Lee et al.¹² A more recent study by Shevchuk et al.,¹³ investigates the stagnation point solution for a rotating disk with simultaneous orthogonal impingement regarding the heat transfer. One can find a comprehensive review relevant to stagnation flow over a rotating disk in the book.¹⁴

This analytical study also explores the effect of surface stretching owing to its several practical applications in the field of metallurgy and chemical engineering. Extrusion processes, fibers spinning, hot rolling, manufacturing of plastic and rubber sheet, continuous casting and glass blowing are examples of industrial applications of stretching of a surface in an ambient fluid. Turkyilmazoglu¹⁵ investigated the three dimensional stagnation point flow of viscous, steady boundary layer of an electrically conducting fluid, in the presence of a magnetic field, due to a rotating disk permitting it to stretch radially. Using spectral technique he solved the governing system of equations numerically and found strong dependence of the stagnation velocities and shear stresses on the rotation parameter, stretching parameter and magnetic field parameter. Recently, Shateyi et al.,¹⁶ extended and studied the steady stagnation-point flow and heat transfer of an electrically conducted incompressible viscous fluid to the case where the disk surface is convectively heated and radially stretched. Though, the study of viscous stagnation point flow due to a stretchable rotating disk has attained considerable attention, very little attention is given to the non-Newtonian counterpart of the same. Therefore, the objective of the present investigation is to extend this study to the non-Newtonian case considering the Reiner-Rivlin fluid model. This fluid model was introduced by Reiner¹⁷ to describe the phenomenon of “dilatancy" and it’s constitutive equation is given by

${\tau }_{ij}\mathrm{<mo>=</mo>}-p{\delta }_{ij}+2\mu e_{ij}+2{\mu }_c{e}_{ik}{e}_{kj}\mathrm{,}{e}_{jj}\mathrm{<mo>=</mo>0}$ (1)

Where p is denoting the pressure, $\mu$ is the coefficient of viscosity and ${\mu }_c$ is the coefficient of cross viscosity. The Reiner-Rivlin model does not predict distinct normal stress differences in simple shear flows and thus the model might be unsuitable for fluids having distinct normal stress differences but many geological, biological materials as well as food products and chemicals are adequately described by this model. In fact the most popular models in chemical engineering, food rheology, glaciology and other areas belong to the class of Reiner-Rivlin fluids. For details one can refer the recent works^18,19 in which the authors have thoroughly discussed about the Reiner-Rivlin fluid.

In this study, we use the popular and promising technique, called, Homotopy Analysis Method (HAM) devised by Liao,²⁰ to produce approximate analytical solutions for the considered problem. The homotopy analysis method is unique among other perturbation techniques as it allows us to effectively control the region of convergence and rate of convergence of a series solution to a nonlinear differential equation, via control of an initial approximation, an auxiliary linear operator, an auxiliary function and a convergence control parameter. Moreover, many other methods such as homotopy perturbation method, Adomian’s decomposition method, -expansion method etc. are special cases of HAM.²¹ A few successful implementation of HAM can be found in the works.^22–24

The rest of the paper is structured as follows: Section 2 presents the formulation of the problem which is followed by application of HAM to the resulting system of nonlinear differential equations in Section 3. The convergence of the obtained solution series is discussed in Section 4. Results are discussed in Section 5 and finally, conclusions are drawn in Section 6.

 Let us consider steady stagnation point flow of a non-Newtonian Reiner-Rivlin fluid due to a stretchable rotating disk of infinite dimension placed at $z\mathrm{<mo>=</mo>0}$ . The disk is assumed to rotate with uniform angular velocity $\Omega$  which stretches radially with constant rate $c$ , (Figure 1). Using cylindrical polar coordinates to describe the flow, let $u\mathrm{,}v\mathrm{,}w$  be the components of velocity along $r\mathrm{,}\varphi \mathrm{,}z$ respectively. And in view of rotational symmetry taking $\frac{\partial }{\partial \varphi }\mathrm{<mo>=</mo>0}$ , the equation of continuity, motion and energy read as:
$\frac{\partial u}{\partial r}+\frac{u}{r}+\frac{\partial w}{\partial z}\mathrm{<mo>=</mo>0}$                                                                             (2)
$\rho \mathrm{<mo\; stretchy="false">(</mo>}u\frac{\partial u}{\partial r}-\frac{v^2}{r}+w\frac{\partial u}{\partial z}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{\partial {\tau }_{rr}}{\partial r}+\frac{\partial {\tau }_{rz}}{\partial z}+\frac{{\tau }_{rr}-{\tau }_{\theta \theta }}{r}$                               (3)
$\rho \mathrm{<mo\; stretchy="false">(</mo>}u\frac{\partial v}{\partial r}+\frac{uv}{r}+w\frac{\partial v}{\partial z}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{\partial {\tau }_{r\theta }}{\partial r}+\frac{\partial {\tau }_{\theta z}}{\partial z}+\frac{2{\tau }_{r\theta }}{r}$                                     (4)
$\rho \mathrm{<mo\; stretchy="false">(</mo>}u\frac{\partial w}{\partial r}+w\frac{\partial w}{\partial z}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{\partial {\tau }_{zr}}{\partial r}+\frac{\partial {\tau }_{zz}}{\partial z}+\frac{{\tau }_{rz}}{r}$                                               (5)
$\rho c_p\left(u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z}\right)\mathrm{<mo>=</mo>}k\left(\frac{1}{r}\frac{\partial T}{\partial r}+\frac{{\partial }^{2}T}{\partial r^2}+\frac{{\partial }^{2}T}{\partial z^2}\right)$                                 (6)

Where, $T$  is fluid’s temperature, $c_p$  and $k$ are specific heat constant and thermal conductivity of the fluid respectively. And the boundary conditions are:

$u\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo><mo>=</mo>}cr\mathrm{,}v\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo><mo>=</mo>}r\Omega \mathrm{,}w\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo><mo>=</mo>0,}T\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo><mo>=</mo>}{T}_w$                               (7)
$u\mathrm{<mo\; stretchy="false">(</mo>}\infty \mathrm{<mo\; stretchy="false">)</mo>}\to ar\mathrm{,}v\mathrm{<mo\; stretchy="false">(</mo>}\infty \mathrm{<mo\; stretchy="false">)</mo>}\to \mathrm{0,}w\mathrm{<mo\; stretchy="false">(</mo>}\infty \mathrm{<mo\; stretchy="false">)</mo>}\to -2az\mathrm{,}T\mathrm{<mo\; stretchy="false">(</mo>}\infty \mathrm{<mo\; stretchy="false">)</mo>}\to T_{\infty }$
Where, a is a constant, $T_w$  is the temperature at the surface of the disk and $T_{\infty }$  is the temperature far away from the disk. Next we use the following similarity transformations:
$u\mathrm{<mo>=</mo>}ar{F}^{\prime }\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>,}v\mathrm{<mo>=</mo>}arG\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>,}w\mathrm{<mo>=</mo>}-2\sqrt{a\nu }F\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>,}\theta \mathrm{<mo>=</mo>}\frac{T-T_{\infty }}{T_w-T_{\infty }}$         (8)
where, $\eta \mathrm{<mo>=</mo>}\sqrt{\frac{a}{\nu }}z$ and the governing equations are reduced to:
$\frac{d^{3}F}{d{\eta }^3}-{\left(\frac{dF}{d\eta }\right)}^2+G^2+2F\frac{d^{2}F}{d{\eta }^2}-\frac{L}{2}\left({\left(\frac{d^{2}F}{d{\eta }^2}\right)}^2+2\frac{dF}{d\eta }\frac{d^{3}F}{d{\eta }^3}+3{\left(\frac{dG}{d\eta }\right)}^2\right)+\mathrm{1<mo>=</mo>0}$ (9)
$\frac{d^{2}G}{d{\eta }^2}+2F\frac{dG}{d\eta }-2\frac{dF}{d\eta }G+L\left(\frac{d^{2}F}{d{\eta }^2}\frac{dG}{d\eta }-\frac{dF}{d\eta }\frac{d^{2}G}{d{\eta }^2}\right)\mathrm{<mo>=</mo>0}$                 (10)
$\frac{d^2\theta }{d{\eta }^2}+2PrF\frac{d\theta }{d\eta }\mathrm{<mo>=</mo>0}$                                                                       (11)

with the boundary conditions
$\begin{array}{l}F\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo><mo>=</mo>0,}G\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo><mo>=</mo>}\omega \mathrm{,}{F}^{\prime }\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo><mo>=</mo>}s\mathrm{,}\theta \mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo><mo>=</mo>1}\hfill \\ F^{\prime }\mathrm{<mo\; stretchy="false">(</mo>}\infty \mathrm{<mo\; stretchy="false">)</mo>}\to \mathrm{1,}G\mathrm{<mo\; stretchy="false">(</mo>}\infty \mathrm{<mo\; stretchy="false">)</mo>}\to \mathrm{0,}\theta \mathrm{<mo\; stretchy="false">(</mo>}\infty \mathrm{<mo\; stretchy="false">)</mo>}\to 0\hfill \end{array}$ (12)
where $\mathrm{<mo>\text{'}</mo>}$  denotes derivatives with respect to$\begin{array}{cc}\eta ,& s\mathrm{<mo>=</mo>}\frac{c}{a}\end{array}$  is the stretching parameter, $\omega \mathrm{<mo>=</mo>}\frac{\Omega }{a}$  is the rotation number, $Pr\mathrm{<mo>=</mo>}\frac{\mu c_p}{k}$  is the Prandtl number and $L\mathrm{<mo>=</mo>}\frac{{\mu }_{c}a}{\mu }$  is the non-Newtonian parameter.

The heat transfer from the disk’s surface to the fluid is computed by the application of Fourier’s law, $q\mathrm{<mo>=</mo>}-k{\left(\frac{\partial T}{\partial z}\right)}_w$  which upon introducing the transformed variables become
$-k\mathrm{<mo\; stretchy="false">(</mo>}{T}_w-T_{\infty }\mathrm{<mo\; stretchy="false">)</mo>}\sqrt{\frac{a}{\nu }}\frac{d\theta \mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}{d\eta }$                                                                   (13)
By rewriting the heat transfer results in terms of the Nusselt number defined as $N_u\mathrm{<mo>=</mo>}\frac{q\sqrt{\frac{\nu }{a}}}{k\mathrm{<mo\; stretchy="false">(</mo>}{T}_w-T_{\infty }\mathrm{<mo\; stretchy="false">)</mo>}}$ , we get
$N_u\mathrm{<mo>=</mo>}-\frac{d\theta \mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}{d\eta }$                                                                                (14)
In terms of variables of the analysis, the expressions for the tangential shear stress ${\tau }_{\theta }$  and radial shear stress ${\tau }_r$  are given by
${\tau }_{\theta }\mathrm{<mo>=</mo>}\frac{{\tau }_{\theta z}}{a\mu r\sqrt{\frac{a}{\nu }}}{\mathrm{<mo>|</mo>}}_{z\mathrm{<mo>=</mo>0}}\mathrm{<mo>=</mo>}{G}^{\prime }\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}-L{G}^{\prime }\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}{F}^{\prime }\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}$        (15)
And
${\tau }_r\mathrm{<mo>=</mo>}\frac{{\tau }_{rz}}{a\mu r\sqrt{\frac{a}{\nu }}}{\mathrm{<mo>|</mo>}}_{z\mathrm{<mo>=</mo>0}}\mathrm{<mo>=</mo>}{F^{\prime }}^{\prime }\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}-L{F^{\prime }}^{\prime }\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}{F}^{\prime }\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}$                                       (16)

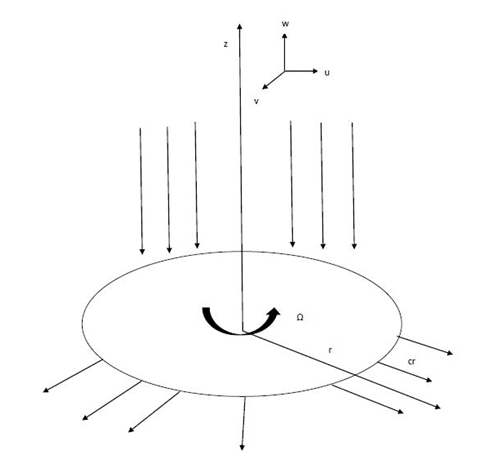
Figure 1 Schematic diagram of the flow domain.

 For this problem, due to the boundary conditions (12), we choose the base function $\mathrm{<mo>\{</mo>}{\eta }^m{e}^{-n\eta }\mathrm{<mo>|</mo>}m\ge 0n\ge \mathrm{0<mo>\}</mo>}$  to express $F\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>,}G\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}$  and $\theta \mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}$ . And the initial approximations are chosen as
$F_0\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo><mo\; stretchy="false">(</mo>}s-\mathrm{1<mo\; stretchy="false">)</mo>}+\eta -\mathrm{<mo\; stretchy="false">(</mo>}s-\mathrm{1<mo\; stretchy="false">)</mo>}{e}^{-\eta }\mathrm{,}$                                                     (17)
$G_0\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\omega e^{-\eta }\mathrm{.}$                                                                                (18)
${\theta }_0\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{e}^{-\eta }$                                                                                    (19)
and the auxiliary linear operators $L_F\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">)</mo>,}{L}_G\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">)</mo>}$  and $L_{\theta }\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">)</mo>}$  as:
$L_F\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{{f^{\prime }}^{\prime }}^{\prime }+{f^{\prime }}^{\prime }\mathrm{,}$                                                                         (20)
$L_G\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{f^{\prime }}^{\prime }+f^{\prime }$                                                                            (21)
$L_{\theta }\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{f^{\prime }}^{\prime }+f^{\prime }$                                                                            (22)
with the following properties
$L_F\mathrm{<mo\; stretchy="false">(</mo>}{c}_1+c_2\eta +c_3{e}^{-\eta }\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0}$                                                                 (23)
$L_G\mathrm{<mo\; stretchy="false">(</mo>}{c}_4+c_5{e}^{-\eta }\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0}$                                                                         (24)
$L_{\theta }\mathrm{<mo\; stretchy="false">(</mo>}{c}_6+c_7{e}^{-\eta }\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0}$                                                                         (25)
where, $c_i\mathrm{,}i\mathrm{<mo>=</mo>1}-7$  are arbitrary constants.
The zero-order deformation equations are constructed as follows:
$\mathrm{<mo\; stretchy="false">(</mo>1}-q\mathrm{<mo\; stretchy="false">)</mo>}{L}_F\mathrm{<mo\; stretchy="false">[</mo>}\widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}-F_0\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo><mo>=</mo>}q{\widehat{H}}_F{\hslash }_F{N}_F\mathrm{<mo\; stretchy="false">[</mo>}\widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>,}\widehat{G}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>,}\widehat{\theta }\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo>}$ (26)
$\mathrm{<mo\; stretchy="false">(</mo>1}-q\mathrm{<mo\; stretchy="false">)</mo>}{L}_G\mathrm{<mo\; stretchy="false">[</mo>}\widehat{G}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}-G_0\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo><mo>=</mo>}q{\widehat{H}}_G{\hslash }_G{N}_G\mathrm{<mo\; stretchy="false">[</mo>}\widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>,}\widehat{G}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>,}\widehat{\theta }\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo>}$  (27)
$\mathrm{<mo\; stretchy="false">(</mo>1}-q\mathrm{<mo\; stretchy="false">)</mo>}{L}_{\theta }\mathrm{<mo\; stretchy="false">[</mo>}\widehat{\theta }\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}-{\theta }_0\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo><mo>=</mo>}q{\widehat{H}}_{\theta }{\hslash }_{\theta }{N}_{\theta }\mathrm{<mo\; stretchy="false">[</mo>}\widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>,}\widehat{G}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>,}\widehat{\theta }\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo>}$  (28)
and the relevant boundary conditions are given by:
$\begin{array}{l}\widehat{F}\mathrm{<mo\; stretchy="false">(</mo>0<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0,}\widehat{G}\mathrm{<mo\; stretchy="false">(</mo>0<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\omega \mathrm{,}\frac{\partial \widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }{\mathrm{<mo>|</mo>}}_{\eta \mathrm{<mo>=</mo>0}}\mathrm{<mo>=</mo>}s\mathrm{,}\widehat{\theta }\mathrm{<mo\; stretchy="false">(</mo>0<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>1}\hfill \\ \frac{\partial \widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }{\mathrm{<mo>|</mo>}}_{\eta \to \infty }\to \mathrm{1,}\widehat{G}\mathrm{<mo\; stretchy="false">(</mo>}\infty \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}\to \mathrm{0,}\widehat{\theta }\mathrm{<mo\; stretchy="false">(</mo>}\infty \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}\to 0.\hfill \end{array}$           (29)
Where the nonlinear differential operators, $N_F\mathrm{,}{N}_G$  and $N_{\theta }$  are defined by:
$\begin{array}{l}{N}_F\mathrm{<mo>=</mo>}\frac{{\partial }^3\widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}}{\partial {\eta }^3}-{\left(\frac{\partial \widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }\right)}^2+{\left(\widehat{G}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}\right)}^2+2\widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}\frac{{\partial }^2\widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}}{\partial {\eta }^2}-\hfill \\ \frac{L}{2}\left({\left(\frac{{\partial }^2\widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}}{\partial {\eta }^2}\right)}^2+2\frac{\partial \widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }\frac{{\partial }^3\widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}}{\partial {\eta }^3}+3{\left(\frac{\partial \widehat{G}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }\right)}^2+1\right)\hfill \end{array}$  (30)
$\begin{array}{l}{N}_G\mathrm{<mo>=</mo>}\frac{{\partial }^2\widehat{G}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}}{\partial {\eta }^2}+2\widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}\frac{\partial \widehat{G}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }-2\frac{\partial \widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }\widehat{G}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}\hfill \\ +L\left(\frac{{\partial }^2\widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}}{\partial {\eta }^2}\frac{\partial \widehat{G}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }-\frac{\partial \widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }\frac{{\partial }^2\widehat{G}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}}{\partial {\eta }^2}\right)\hfill \end{array}$             (31)
$N_{\theta }\mathrm{<mo>=</mo>}\frac{{\partial }^2\widehat{\theta }\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}}{\partial {\eta }^2}+2Pr\widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}\frac{\partial \widehat{\theta }\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }$                                           (32)
Clearly, when q varies from 0 to 1, $\widehat{F}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>,}\widehat{G}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}$ and $\widehat{\theta }\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo>;</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}$  varies from the initial approximations $F_0\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>,}{G}_0\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>,}{\theta }_0\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}$  to the original solutions $F\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>,}G\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>,}\theta \mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}$ . Next, following the procedure similar to Liao¹¹, we have the high order approximations for $F_m\mathrm{,}{G}_m\mathrm{,}{\theta }_m$ , called, $m^{th}$ -order deformation equations
$L_F\mathrm{<mo\; stretchy="false">[</mo>}{F}_m\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}-{\chi }_m{F}_{m-1}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo><mo>=</mo>}{\widehat{H}}_F{\hslash }_F{R}_m^F$                                              (33)
$L_G\mathrm{<mo\; stretchy="false">[</mo>}{G}_m\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}-{\chi }_m{G}_{m-1}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo><mo>=</mo>}{\widehat{H}}_G{\hslash }_G{R}_m^G$                                             (34)
$L_{\theta }\mathrm{<mo\; stretchy="false">[</mo>}{\theta }_m\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}-{\chi }_m{\theta }_{m-1}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo><mo>=</mo>}{\widehat{H}}_{\theta }{\hslash }_{\theta }{R}_m^{\theta }$                                                (35)
$F_m\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo><mo>=</mo>}{G}_m\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo><mo>=</mo>}{F}_{m^{\prime }}\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo><mo>=</mo>}{\theta }_m\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo><mo>=</mo>}{F}_{m^{\prime }}\mathrm{<mo\; stretchy="false">(</mo>}\infty \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{G}_m\mathrm{<mo\; stretchy="false">(</mo>}\infty \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\theta }_m\mathrm{<mo\; stretchy="false">(</mo>}\infty \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0}$   (36)
where, $R_m^F\mathrm{,}{R}_m^G\mathrm{,}{R}_m^{\theta }$  are given by:
$\begin{array}{l}{R}_m^F\mathrm{<mo>=</mo>}\frac{{\partial }^3{F}_{m-1}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial {\eta }^3}-{\displaystyle \sum _{n\mathrm{<mo>=</mo>0}}^{m-1}}\left(\frac{\partial F_n\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }\frac{\partial F_{m-1-n}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }+G_n\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}{G}_{m-n-1}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}-2F_n\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}\frac{{\partial }^2{F}_{m-1-n}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial {\eta }^2}\right)\hfill \\ -\frac{L}{2}{\displaystyle \sum _{n\mathrm{<mo>=</mo>0}}^{m-1}}\left(\frac{{\partial }^2{F}_n\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial {\eta }^2}\frac{{\partial }^2{F}_{m-1-n}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial {\eta }^2}+2\frac{\partial F_n\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }\frac{{\partial }^3{F}_{m-1-n}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial {\eta }^3}+3\frac{\partial G_n\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }\frac{\partial G_{m-1-n}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }\right)+1-{\chi }_m\hfill \end{array}$  (37)
$\begin{array}{l}{R}_m^G\mathrm{<mo>=</mo>}\frac{{\partial }^2{G}_{m-1}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial {\eta }^2}+2{\displaystyle \sum _{n\mathrm{<mo>=</mo>0}}^{m-1}}\left(2F_n\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}\frac{\partial G_{m-1-n}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }-2\frac{\partial F_n\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }{G}_{m-1-n}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}\right)\hfill \\ +L{\displaystyle \sum _{n\mathrm{<mo>=</mo>0}}^{m-1}}\left(\frac{{\partial }^2{F}_n\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial {\eta }^2}\frac{\partial G_{m-1-n}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }-\frac{\partial F_n\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }\frac{{\partial }^2{G}_{m-1-n}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial {\eta }^2}\right)\hfill \end{array}$ (38)
$R_m^{\theta }\mathrm{<mo>=</mo>}\frac{{\partial }^2{\theta }_{m-1}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial {\eta }^2}+2Pr{\displaystyle \sum _{n\mathrm{<mo>=</mo>0}}^{m-1}}{F}_n\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}\frac{\partial {\theta }_{m-1-n}\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}}{\partial \eta }$                                   (39)
And,
${\chi }_m\mathrm{<mo>=</mo>}(\begin{array}{cc}1& m\mathrm{<mo>></mo>1}\\ 0& m\le 0\end{array}$                                                                            (40)
Finally, choosing the auxiliary functions as ${\widehat{H}}_F\mathrm{<mo>=</mo>}{\widehat{H}}_G\mathrm{<mo>=</mo>}{\widehat{H}}_{\theta }\mathrm{<mo>=</mo>}{e}^{-2\eta }$ , these linear equations (33)-(36) were solved for $F_m\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>,}{G}_m\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>,}{\theta }_m\mathrm{<mo\; stretchy="false">(</mo>}\eta \mathrm{<mo\; stretchy="false">)</mo>}$  and the results are analyzed graphically in section 5.

 To get a proper value of the convergence control parameter, constant $\hslash$ -curves of some special quantities, such as, ${F^{\prime }}^{\prime }\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>,}{G}^{\prime }\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>,}{\theta }^{\prime }\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}$ are drawn and a value from the region that corresponds to the line segments nearly parallel to horizontal axis is chosen to ensure the convergence of the obtained solution series. A few such curves, for different combinations of flow parameters $L\mathrm{,}Pr\mathrm{,}\omega \mathrm{,}s$  are shown in Figure 2.

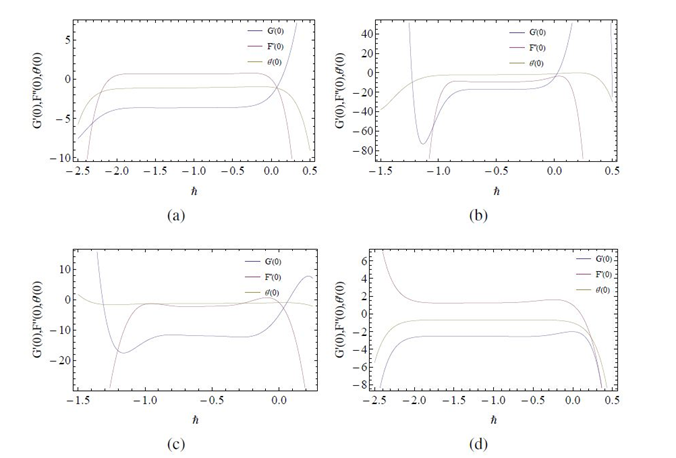
Figure 2 Constant $\hslash$ -curves (A) $\omega \mathrm{<mo>=</mo>2,}Pr\mathrm{<mo>=</mo>1,}L\mathrm{<mo>=</mo>0,}s\mathrm{<mo>=</mo>1}$ . (B) $\omega \mathrm{<mo>=</mo>5,}Pr\mathrm{<mo>=</mo>1,}L\mathrm{<mo>=</mo>0,}s\mathrm{<mo>=</mo>5}$ . (C) $\omega \mathrm{<mo>=</mo>5,}Pr\mathrm{<mo>=</mo>1,}L\mathrm{<mo>=</mo>0.1,}s\mathrm{<mo>=</mo>2}$ . (D) $\omega \mathrm{<mo>=</mo>2,}Pr\mathrm{<mo>=</mo>1,}L\mathrm{<mo>=</mo>0.3,}s\mathrm{<mo>=</mo>0}.$

We know that for the case when $\hslash \mathrm{<mo>=</mo>}-1$  and the auxiliary function is chosen to be unity, the solutions obtained using HAM can be considered solutions of HPM. Note that, HPM cannot guarantee convergent solution series for any arbitrary combination of the flow parameters and this is clear from Figures 2(B) & (C) as $\hslash \mathrm{<mo>=</mo>}-1$  does not fall inside the valid region of convergence. Moreover, it can be observed from Table 1 & Table 2 that HPM values of $\hslash \mathrm{<mo>=</mo>}-1$  do not converge for the selected values of the relevant parameters. However, HAM provides one with great freedom to chose the auxiliary function and the presence of convergence control parameter in HAM enables one to obtain convergent solution series by controlling and adjusting the region of convergence whenever necessary. In view of the superiority of HAM over HPM, HAM is used to investigate this problem and the results obtained using ${10}^{th}$ -order homotopy approximations are plotted for different combinations of the flow parameters.

This section presents the variation of velocity and temperature fields with stretching, rotation, and non-Newtonian parameter graphically, obtained using ${10}^{th}$ -order homotopy approximations. To validate the results obtained using HAM, first the Newtonian case is considered. For this case, that is, when $L\mathrm{<mo>=</mo>0}$  variations of the flow fields with stretching parameter $s$  are plotted in Figure 3 when $\omega \mathrm{<mo>=</mo>2}$  and in Figure 4 when $\omega \mathrm{<mo>=</mo>5}$ , keeping the Prandtl number $Pr\mathrm{<mo>=</mo>1}$  fixed. The radial velocity $F^{\prime }$ increases near the wall with increasing stretching whereas the axial ($-F$ ) and azimuthal velocity ($G$ ) decreases. The temperature distribution is also seen to decrease attaining its limiting value nearer to disk surface with increasing values of $s$ . For higher rotation rate one can observe from Figure 4, that the radial velocity initially increases exceeding its asymptotic value for some small values of $s$ , gradually decreasing for higher values of $s$ . These observations are in agreement with those reported by Turkyilmazoglu.¹⁵ Moreover, a comparison of the values of shear stresses (radial and tangential) with those reported in¹⁵ (in his paper, in Tables 2−4 for $M\mathrm{<mo>=</mo>0}$ ) shows a good agreement, see Figure 5(A) & Figure (B).

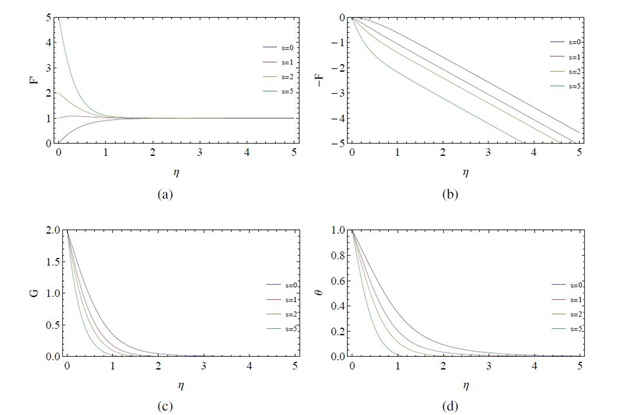
Figure 3 Variation of velocity and temperature profiles with stretching parameter s for $L\mathrm{<mo>=</mo>0,}\omega \mathrm{<mo>=</mo>2,}Pr\mathrm{<mo>=</mo>1}$  (A) Radial. (B) Axial. (C) Azimuthal. (D) temperature.

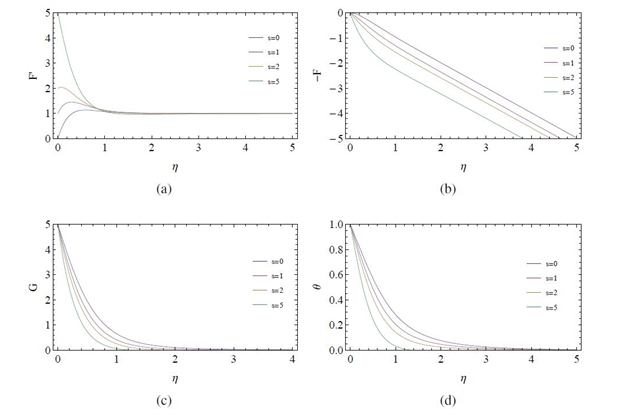
Figure 4 Variation of velocity and temperature profiles with stretching parameter s for $L\mathrm{<mo>=</mo>0,}\omega \mathrm{<mo>=</mo>2,}Pr\mathrm{<mo>=</mo>1}$ (A) Radial. (B) Axial. (C) Azimuthal. (D) Temperature.

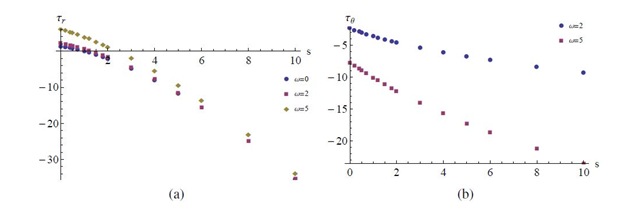
Figure 5 Variation of radial and tangential stresses with stretching for Newtonian case ($L\mathrm{<mo>=</mo>0}$ ), (A) Radial stress ${\tau }_r$ . (B) Tangential stress ${\tau }_{\theta }$ .

Effect of stretching parameter on the non-Newtonian flow profiles are shown in Figure 6 & Figure 7. Axial istributions of flow fields are plotted for $\omega \mathrm{<mo>=</mo>2}$  in Figure 6 and $\omega \mathrm{<mo>=</mo>5}$  in Figure 7, keeping $L\mathrm{<mo>=</mo>0.1,}Pr\mathrm{<mo>=</mo>1}$  fixed.

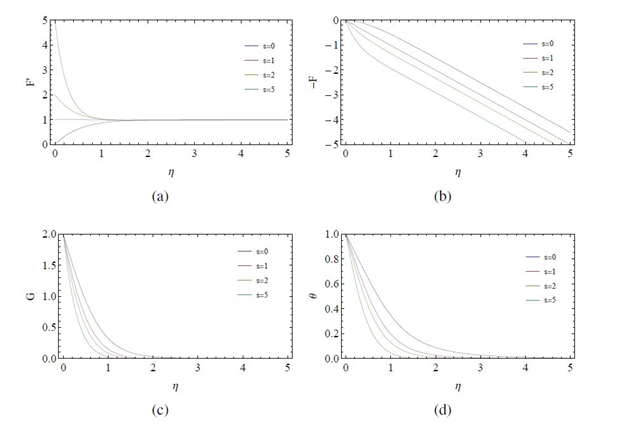
Figure 6 Variation of velocity and temperature profiles with stretching parameter s for $L\mathrm{<mo>=</mo>0.1,}\omega \mathrm{<mo>=</mo>2,}Pr\mathrm{<mo>=</mo>1}$  (A) Radial. (B) Axial. (C) Azimuthal. (D) Temperature.

 It is clear from Figure 6(A) & Figure (B), Figures 7(A) & Figure (B), that for this case, behavior similar to the Newtonian case can be observed, as with increasing stretching (rotation), centrifugal force pushes the fluid particles in the radial direction which is balanced by particles which are drawn to the disk due to surface stretching in the negative axial direction. Also, disk’s angular velocity and temperature distributions decrease as stretching increases.

The case of stagnation point flow due to a stationary disk, that is, when the disk does not rotate and there is no radial stretching ($\omega \mathrm{<mo>=</mo>0,}s\mathrm{<mo>=</mo>0}$ ), is presented in Figure 8. This case is analogous to the case of three dimensional axisymmetric stagnation flow over a flat plate. The Newtonian velocity and temperature fields displayed in Figure 8(A) and the effect of non-Newtonian parameter on the flow fields can be observed from Figures 8(B)−8(D). Since the disk is not rotating, the azimuthal component of velocity is zero for this case. The flow consists of an inward axial flow which upon striking the stationary disk is thrown radially outward inside the boundary layer and heat transfer is from the surface of the disk to the fluid, which decreases gradually from its starting value at the surface of the disk to its limiting value as it moves away from the disk. It can be seen that increasing $L$ , increases the magnitude of radial velocity whereas the axial velocity decreases. In Figure 8(D) enlarged view of the temperature profiles are shown and it is clear that magnitude of temperature distributions decreases with increasing values of $L$ .

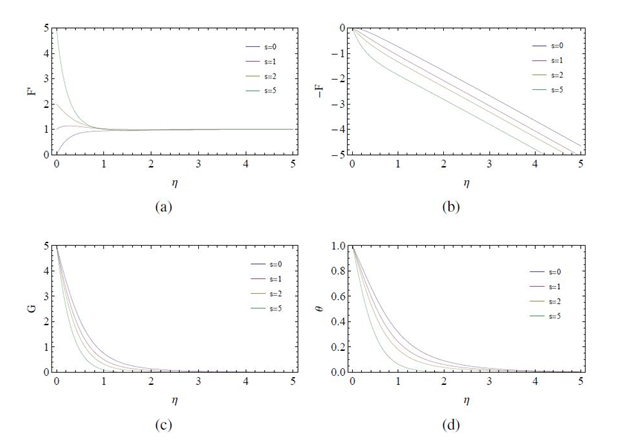
Figure 7 Variation of velocity and temperature profiles with stretching parameter s for $L\mathrm{<mo>=</mo>0.1,}\omega \mathrm{<mo>=</mo>5,}Pr\mathrm{<mo>=</mo>1}$  (A) radial. (B) Axial. (C) Azimuthal. (D) Temperature.

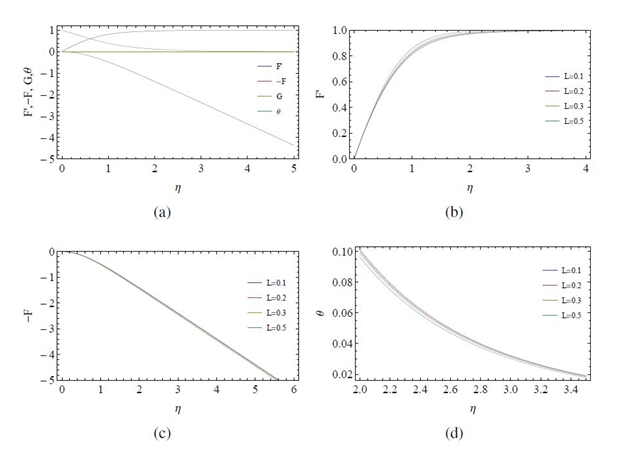
Figure 8 The case of stagnation point flow due to a stationary disk ($s\mathrm{<mo>=</mo>0,}\omega \mathrm{<mo>=</mo>0}$ ) (A) Newtonian velocity and temperature fields. (B) Radial. (C) Axial. (D) Temperature.

In Figure 9, we have presented the case of stagnation point flow towards a radially stretching disk ($\omega \mathrm{<mo>=</mo>0,}s\mathrm{<mo>=</mo>2}$ ). This scenario is similar to the axisymmetric stagnation flow towards a stretchable surface. Newtonian profiles are shown in Figure 9(A) and from Figures 9(B)−9(D) shows the effect of $L$  on the velocity and temperature fields. Again, azimuthal velocity is zero due to no rotation of the disk and due to the presence of surface stretching, axial fluid impinging on disk’s surface is cast away radially near the surface of the disk. Analogous to the earlier observations, temperature $\theta$  is maximum at the surface the disk and it deceases with $\eta$  attaining it’s limiting value at sufficiently large $\eta$ . Moreover, the increasing effect of $L$  is to increase the value of $\theta$  at all nonzero $\eta$ . The values of radial component of velocity are found to be increasing for increasing values of the non-Newtonian parameter $L$  and this decrease is balanced by an increase in the values of the axial component of velocity.

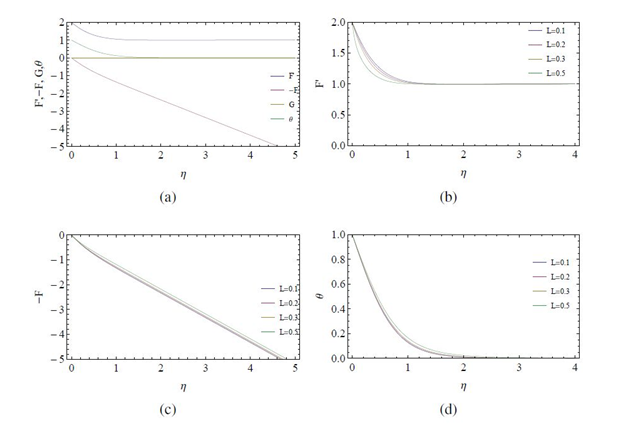
Figure 9  The case of stagnation point flow towards a radially stretching disk ($\omega \mathrm{<mo>=</mo>0,}s\mathrm{<mo>=</mo>2}$ ) (A) Newtonian velocity and temperature fields. (B) Radial. (C) Axial. (D) Temperature.

Next, the case of stagnation point flow towards a rotating disk without radial stretching ($\omega \mathrm{<mo>=</mo>2,}s\mathrm{<mo>=</mo>0}$ ) is presented in Figure 10. Centrifugal forces arising in the flow due to rotation, drives the fluid particles radially away from the disks surface which is compensated by an negative axial flow towards the disk (due to continuity). Angular velocity of the disk and temperature distributions are seen to be decreasing functions of $\eta$ . For this case, Newtonian flow profiles are displayed in Figure 10(A) and the effect of non-Newtonian parameter on the flow fields are displayed in Figures 10(B)−(E). With increasing values of the non-Newtonian parameter $L$  the radial and azimuthal velocities are decreasing whereas the axial velocity and temperature distribution are increasing with increasing $L$ , at all $\eta \ne 0$ .

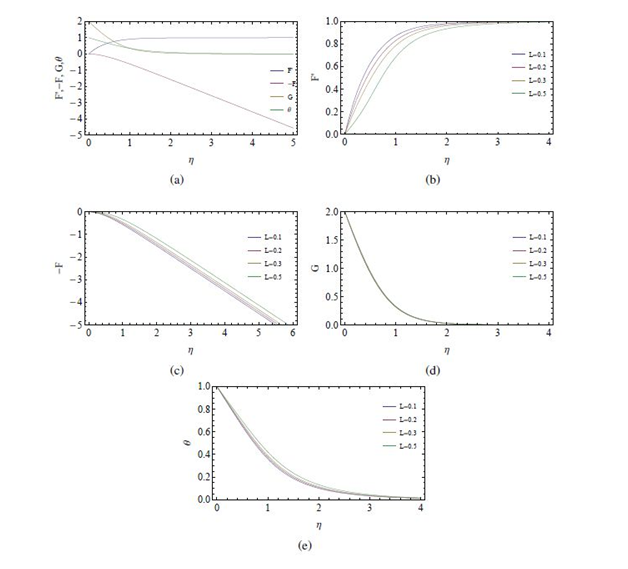
Figure 10 The case of stagnation point flow over a rotating disk ($\omega \mathrm{<mo>=</mo>2,}s\mathrm{<mo>=</mo>0}$ ) (A) Newtonian velocity and temperature fields. (B) Radial. (C) Axial. (D) Azimuthal. (E) Temperature.

When the disk rotates as well as stretches radially ($\omega \mathrm{<mo>=</mo>2,}s\mathrm{<mo>=</mo>2}$ ), for increasing values of the non-Newtonian parameter $L$ , radial and azimuthal components of velocity decreases while axial velocity increases, as can be observed from Figure 11(A)−(C). The temperature distribution is seen to increase and it takes larger distance from the disk to approach its asymptotic value, with increasing values of $L$ .

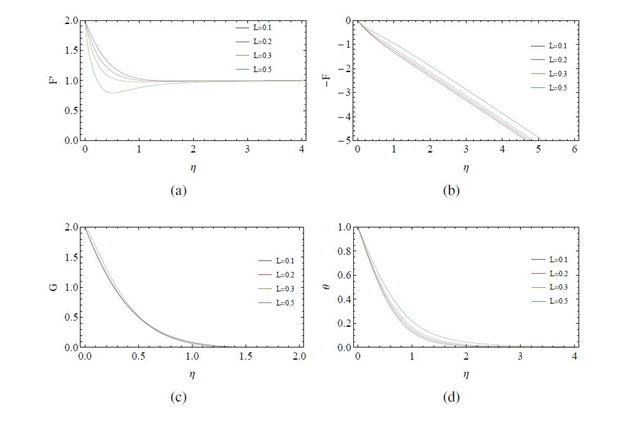
Figure 11 Variation of velocity and temperature profiles with the non-Newtonian parameter L for $\omega \mathrm{<mo>=</mo>2,}s\mathrm{<mo>=</mo>2}$  (A) Radial. (B) Axial. (C) Azimuthal. (D) Temperature.

Figure 12(A) & (B), present the effect of the non-Newtonian parameter on radial and tangential stress. Effect of $L$  on Nusselt number is plotted in Figure 12(C). When the disk is neither rotating nor stretching ($\omega \mathrm{<mo>=</mo>}s\mathrm{<mo>=</mo>0}$ ), radial stress and Nusselt number is found to be increasing for increasing values of $L$ . When $\omega \mathrm{<mo>=</mo>0,}s\mathrm{<mo>=</mo>2}$ , radial stress is increasing but Nusselt number is decreasing with $L$ . For the case, when the disk is rotating without any surface stretching ($\omega \mathrm{<mo>=</mo>}s\mathrm{<mo>=</mo>0}$ ), both the stresses and Nusselt number are decreasing function of $L$ . And when the disk rotates as well as stretches ($\omega \mathrm{<mo>=</mo>}s\mathrm{<mo>=</mo>2}$ ), the effect of increasing the non-Newtonian parameter is to decrease the radial stress and Nusselt number but to increase the tangential stress.

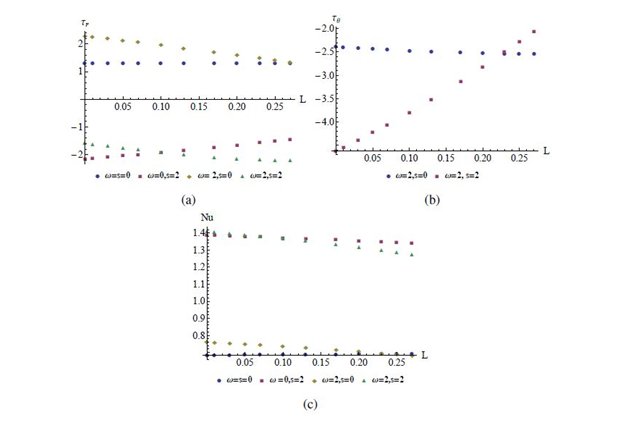
Figure 12 Variation of radial stress, tangential stress and Nusselt number with the non-Newtonian parameter L for different $\omega$  and s when $Pr\mathrm{<mo>=</mo>1}$  (A) Radial stress. (B) Tangential stress. (C) Nusslet number.

In this article, the stagnation point flow of a non-Newtonian Reiner-Rivlin fluid due to a radially stretching, rotating disk is investigated and the effect of different flow parameters such as stretching, rotation, non-Newtonian parameter on the flow fields are discussed in detail using an effective analytical method called Homotopy Analysis Method. The results are verified for the case of Newtonian fluid with the available literature and excellent agreements have been observed. In addition, a comparison of HAM results with those obtained using HPM validates the efficiency of HAM over HPM. Both radial and tangential stresses are found to be decreasing functions of the stretching parameter. Radial stress is seen to decrease from positive values to negative ones whereas the tangential stress starts from a negative value and becomes more and more negative with increasing values of stretching parameter. Moreover, it can be concluded that the present successful implementation of HAM to solve the system of nonlinear equations governing the problem under consideration yet again verifies the effectiveness of the method and thus can be applied to study many other problems of scientific and engineering interest.

None.

Author declares there is no conflict of interest in publishing the article.

1. Karl Hiemenz. Die grenzschicht an einem in den gleichformigen flussigkeitsstrom eingetauchten geraden kreiszlynder. Dingler Polytechnisches Journal. 2011;326:321–324.
2. Fritz Homann. Der einfluss grosser zähigkeit bei der strömung um den zylinder und um die kugel. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik. 1936;16(3):153–164.
3. L Howarth. CxlIV. The boundary layer in three dimensional flow–part II. The flow near a stagnation point. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 1951;42(335):1433–1440.
4. Th V Kármán. Über laminare und turbulente reibung. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik. 1921;1(4):233–252.
5. JT Stuart. On the effects of uniform suction on the steady flow due to a rotating disk. The Quarterly Journal of Mechanics and Applied Mathematics. 1954;7(4):446–457.
6. M Miklacic, CY Wang. The flow due to a rough rotating disk. Zeitschrift für angewandte Mathematik und Physik ZAMP. 2004;55(2):235–246.
7. Tiegang Fang, Ji Zhang. Flow between two stretchable disks-an exact solution of the navier-stokes equations. International Communications in Heat and Mass Transfer. 2008;35(8):892–895.
8. MS Alam, SM Chapal Hossain, MM Rahman. Transient thermophoretic particle deposition on forced convective heat and mass transfer flow due to a rotating disk. Ain Shams Engineering Journal. 2016;7(1):441–452.
9. DM Hannah. Forced flow against a rotating disc. UK: HM Stationery Office, National government publication; 1952. p. 17.
10. H Schlichting, E Truckenbrodt. Die strömung an einer angeblasenen rotierenden scheibe. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik. 1952;32(4-5):97–111.
11. CL Tien, J Tsuji. Heat transfer by laminar forced flow against a non-isothermal rotating disk. International Journal of Heat and Mass Transfer. 1964;7(2):247–252.
12. Min-Hsiun Lee, DR Jeng, KJ De Witt. Laminar boundary layer transfer over rotating bodies in forced flow. J Heat Transfer. 1978;100(3):496–502.
13. IV Shevchuk, N Saniei, XT Yan. Impingement heat transfer over a rotating disk: integral method. Journal of thermophysics and heat transfer. 2003;17(2):291–292.
14. Igor V Shevchuk. Convective heat and mass transfer in rotating disk systems. Volume 45, Germany: Springer Science & Business Media: 2009. p. 236.
15. Mustafa Turkyilmazoglu. Three dimensional MHD stagnation flow due to a stretchable rotating disk. International Journal of Heat and Mass Transfer. 2012;55(23-24):6959–6965.
16. S Shateyi, OD Makinde. Hydromagnetic stagnation-point flow towards a radially stretching convectively heated disk. Mathematical Problems in Engineering. 2013. p. 8.
17. Markus Reiner. A mathematical theory of dilatancy. American Journal of Mathematics. 1945;67(3):350–362.
18. AJM Spencer. Some results in the theory of non-newtonian transversely isotropic fluids. Journal of non-newtonian fluid mechanics. 2004;119(1):83–90.
19. Bruce Caswell. Non-newtonian flow at lowest order, the role of the reiner–rivlin stress. Journal of non-newtonian fluid mechanics. 2006;133(1):1–13.
20. Sh J Liao. The proposed homotopy analysis technique for the solution of nonlinear problems. PhD thesis, China; Shanghai Jiao Tong University: 1992.
21. Shijun Liao. Beyond perturbation: Introduction to the homotopy analysis method. USA: CRC press; 2003. p. 336.
22. Cheng Yang, Shijun Liao. On the explicit, purely analytic solution of von kármán swirling viscous flow. Communications in Nonlinear Science and Numerical Simulation. 2006;11(1):83–93.
23. MM Rashidi, S Bagheri, E Momoniat, et al. Entropy analysis of convective mhd flow of third grade non-newtonian fluid over a stretching sheet. Ain Shams Engineering Journal. 2017;8(1):77–85.
24. Abhijit Das. Analytical solution to the flow between two coaxial rotating disks using ham. Procedia Engineering. 2015;127:377–382.