The kinetics and mechanisms of complete spreading of polydimethylsiloxane (PDMS) droplets on a solid substrate were examined to discern the limits of the hydrodynamic regime and to identify the nature of the subsequent transport processes. Experiments were conducted on PDMS-1000 in comparison with glycerin on soda-lime glass. The kinetic data were analyzed within the context of a thermodynamic framework which accounts for the driving force of droplet spreading as the difference between Laplace pressure and the solid/liquid interfacial energy. As Laplace pressure within the droplet was depleted to a minimum the glycerin droplet ceased to spread and the PDMS droplet was caused to transform into few micrometers thin film spreading in a Fickian-type behavior. The diffusive transport of the liquid film over the solid substrate is probably driven by short range forces. Based on the evidence gathered in this study what is generally accepted as “complete” spreading falls into two distinct regimes: Hydrodynamic regime, and the diffusive regime; each is driven by a different mechanism. In analogy with other liquids, PDMS is suggested to exhibit partial wetting with small, but finite, equilibrial contact angle of about 8 degrees. The diffusive regime is likely a manifestation of the unusual molecular mobility of the PDMS molecules.

Keywords: PDMS, droplet, complete spreading, kinetics

The motion of the three-phase line created by a liquid droplet on a flat solid substrate has been extensively studied for more than a century, yet the constitutive relation governing this motion remains unclear. When a liquid droplet is placed in contact with a flat substrate, the system is driven towards equilibrium. The contact angle relaxes from its initial value at the moment of contact, towards its equilibrium angle, ${\theta }_{\infty }$ . The system is believed to be in equilibrium when its configuration satisfies minimal energy, described by the Young-Dupree equation, i.e.,
${\gamma }_{1}cos\theta ={\gamma }_2–{\gamma }_{12}$                     (1)
Where ${\gamma }_1$ is the surface tension of the liquid, ${\gamma }_2$ is the surface energy of the solid-vapor interface, and ${\gamma }_{12}$ is the energy of the liquid-solid interface. The concepts underlying this equation have been instrumental in advancing many interfacial technologies. However, despite the great deal of experimental measurements of surface tension of liquids and contact angles of various liquid/solid pairs, the liquid/solid interfacial energy and the surface energy of the solid remain inaccessible.

An ingenious approach was developed by Zisman¹ to estimate a critical energy of wetting (Wettability), a quantity that may be associated with the surface energy of the solid substrate,${\gamma }_2$ . According to Zisman,¹ contact angles of a homologous series of liquids having different surface tensions are extrapolated to$cos\theta =1$ . This condition, in view of Eq. 1, equates ${\gamma }_{12}$  associated with a specific solid and a hypothetical liquid with the difference${\gamma }_2–{\gamma }_1$ .

The rate at which a liquid droplet spreads from $\theta =180°$ to reach equilibrium at ${\theta }_{\infty }$  has been described at the macroscopic level by an energy balance between capillary driving force and hydrodynamic resistance.²⁻⁸ The models produce power law relationships between the contact radius and time or contact angle and time. The macroscopic parameters of these laws are the surface tension and the viscosity of the liquid. Contributions of the solid-vapor interface and the solid-liquid interface; which are fundamental quantities in the Young-Dupree equation are introduced implicitly as a correction factor of the form ${\gamma }_1(cos{\theta }_{\infty }–cos\theta )$ .³ Recent results have shown that these models describe the spreading of PDMS on glass substrate; yet depart significantly from the kinetics of a host of other liquids on soda-lime glass⁹ and other solids.¹⁰

Perhaps the preeminence of Hoffman’s⁴ work had driven the majority of subsequent experiments to consider PDMS/glass as the interface of choice. That PDMS droplets are believed to exhibit zero contact angles at equilibrium on most solids, its spreading has been labeled “complete”. All other liquids have accordingly been classified as “incomplete”. Ambiguous as it may be, the introduction “complete” spreading as a separate class raises a number of issues. In recent study¹¹ revealed that the initial viscous regime either lasts in its entirety or switches to an intermediate inertial regime where the spreading radius grows with time following the well-established inertial scaling.¹¹ First it obscures the eventual changeover from Laplace (hydrodynamic) regime to Fickian-like (diffusive) mobility as the film thickness becomes infinitesimally small. Indeed an investigation¹² concludes that the process through which the molecules pass from the main drop to the monolayer is not fully understood and attributes that to a “missing link”. That almost all liquids except PDMS, to the best of our knowledge, exhibit non-zero contact angles categorizes them all as “incomplete”, i.e., exception of the “complete” norm.

In an attempt to discern the ending of the hydrodynamic regime of “complete” droplet spreading the present study examines the mechanisms and kinetics of the process within a more rigorous thermodynamic framework. The study contrasts the behavior of two liquids; PDMS (complete) and glycerin (incomplete) to verify the similarity of the processes in both cases. It is hoped that the results will assist in the realization of a more scientific account of the phenomenon.

It is commonly theorized that capillary forces balanced by viscous resistance are the sole forces acting in the spreading process. Thus continuum based kinetic equations relate the rate of spreading to the surface tension and the viscosity; both are properties of the liquid. Nevertheless, a liquid droplet in equilibrium on a solid substrate is a system governed by the three energies defined by the Young-Dupree equation. As the contact line moves towards equilibrium, viscous dissipation processes control its rate. An investigation¹⁰ has shown that the solid substrate plays a significant role in equilibrium spreading as well as the rate at which it is achieved. It is therefore essential to re-examine the thermodynamic foundation of the process.

As the contact line moves, the system creates a contact interface of a specific energy of ${\gamma }_{12}$  and area of A. This happens at the expense of solid vapor interface. Viscous processes produce the necessary dissipation. The following scenario is proposed as a qualitative framework.
The droplet is a curved surface reservoir whose pressure is determined by the surface tension g1 and the radius of curvature$\rho$  (Figure 1) in accordance with Young-Laplace equation, i.e.,
$\Delta P=\frac{2{\gamma }_1}{\rho }$                                                (2)
The radius of curvature as seen in the figure is related to the contact radius Rc ¹³ as
$\rho =\frac{R_c}{\sin \theta }$                                                 (3)
It is imperative to note that as the contact area increases, the radius of curvature increases giving rise to a corresponding lessening Laplace pressure, which amounts to a continual decrease in the driving force. Consequently the spreading must cease to grow when the driving component can no longer overcome its resistance. The latter is obviously dictated by the specific nature of the liquid/solid pair.

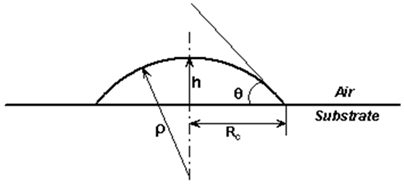
Figure 1 Schematic representation of the spreading droplet using spherical cap approximation: R_c is the radius of the droplet-substrate contact area, is the radius of curvature, and h is the height of the droplet with respect to the surface.

The formation of a contact interface is regarded to resist the flow driven by Laplace pressure, therefore “A12 g12” may be thought of as the resisting component of the driving force. Contributions of the solid/vapor interface may be assumed to act through${\gamma }_{12}$ .

Dissipative processes include those commonly attributed to the viscosity of the liquid m1 and the recently discovered interfacial viscosity, ${\mu }_{12}$ .¹⁰ Whereas the former takes place within the droplet, the latter is suggested to prevail within the advancing foot.

With the above framework, we proceed to analyze the spreading kinetics of the two liquids, PDMS and glycerin. The two liquids possess similar viscosities and different surface tensions. The two liquids are classified to exhibit “complete” and “incomplete” spreading, respectively.

The liquids were trimethyl-terminated polydimethylsiloxanes, PDMS and glycerin (Fluka Chemika Company, Buchs, Switzerland). PDMS has a surface tension of ${\gamma }_1=21.5mN/m$  and a viscosity of 1000 cp. Glycerin has a surface tension of ${\gamma }_1=67.6mN/m$  and a viscosity of 954 cP.

Soda-lime glass slides (26x26 mm) (Menzel-Glaser Company, Geschnitten, Germany) were cleaned by immersion in Chromic acid solution for 4 hours followed by a thorough rinsing with distilled water then further cleaned with acetone (99.5% purity, Panreac, Barcelona, Spain). The clean slides were subsequently dried in a vacuum oven at 70 °C for 30 minutes, at the end of which the temperature was switched off and the slides were allowed to cool under vacuum. Subsequently the slides were carefully transferred to a desiccators, where they were stored until the time of use. Each cleaned, dried glass slide was used only for a single measurement. Effectiveness of the cleaning and drying procedures on the cleanness of the glass surface was assured by examining sample slides before and after cleaning using a scanning electron microscope (JEOL jsm5600, Japan) at 5,000 magnifications. The quality of surface roughness and heterogeneity was inspected by measuring contact angle hysteresis of cleaned silica-lime glass surface. The contact angle hysteresis was determined by taking the difference between the advancing and the receding contact angles measurements. For water on silica-lime glass surfaces, the measured contact angle hysteresis was found within 6-9°.⁹ It should be pointed out that, although the glass surfaces used in this study are very smooth, they may still have a very small percentage of heterogeneity probably due to the exposure of glass slides to the laboratory ambient conditions. This might be the cause of the observed contact angle hysteresis.

The experimental setup was described elsewhere.⁹ A $1.5\mu l$  droplet was charged from a micro-syringe (SGE International Company, Australia). The tip of the syringe was positioned a few micrometers from the surface of the glass to eliminate impact effects upon the release of the droplet. The droplet volume used assured that gravity effects were negligible. Digital video camera (JVC TK-c1380, Japan) with 10x eyepiece magnification, placed underneath the glass slide, and interfaced with a PC equipped with a frame grabber and an image analysis system (analySIS soft Imaging System, GmbH ltd, Germany). Each data point presents an average value of ten measurements at least. The standard deviation calculated for each data point found to be less than 6%. All experiments were carried at ambient conditions, i.e., 25±1°C and 47%±3%RH.

Figure 2 & Figure 3 present the contact area as a function of time for identical droplets’ volumes of PDMS and glycerin on glass, respectively. Whereas the glycerin droplet reached equilibrium at a contact area of about 0.08cm² within slightly less than 200 seconds, the PDMS droplet continued to spread over the time frame allowed. The PDMS experiment was interrupted at 1600 seconds when the contact area reached 0.3cm² and was still advancing. Calculations of the contact angles based on spherical cap approximation were 25o for glycerin at equilibrium. The value of ${\theta }_{\infty }$  for glycerin was in agreement with that determined from contact angle measurements. As for PDMS, if the curve in Figure 2 was to be extrapolated, “complete” wetting require a very long time.

Figure 2 Typical data of PDMS-1000 droplet spreading over time.

Figure 3 Typical data of glycerin droplet spreading over time.

Whereas the entire history of the glycerin droplet and the early portion of the PDMS droplet may be reasonably approximated as a spherical cap, at a later stage the spread droplet is more realistically approximated as a pancake;⁷ where the droplet height of the pancake is half the spherical cap height. Figure 4 shows the applicability of both approximations for the droplets. As suggested, the PDMS droplet resembles a spherical cap in its early stage and bears better resemblance to a pancake at and beyond 1000 seconds. Here, attention is drawn to the implication that the film thickness at sufficiently long time would approach a few microns.

Estimates of Laplace pressure difference for both droplets are shown in Figure 5. The pressure difference decays rapidly with time to a finite plateau of 38N/m² at about 200 seconds for the glycerin droplet. Similarly, the pressure difference associated with the PMDS droplet decays to about 2N/m² at about 250 seconds, beyond which further decay appeared negligible. Recalling that the pressure difference, according to the thermodynamic framework described above, represents the active component of the driving force, it is not surprising to note the congruence of the time at which equilibrium was reached (Figure 3) and that at which the pressure difference reached its plateau. On basis of Young’s equation the spreading coefficient:
$S={({\gamma }_2–{\gamma }_1)}_{-}{\gamma }_{12}$                                    (4)

defines the magnitude of spontaneous spreading of a specific liquid-solid pair. “Complete” spreading is achieved when for S=0. Current literature speak of two limiting cases: “complete” wetting exhibited by silicone oil (S = 0) and none wetting exhibited by mercury on most solid substrates$(S\to \infty )$ . The wetting behavior of other liquid-solid pairs apparently falls within these two extreme cases and the magnitude of equilibrium wetting depends on the values of all three interfacial parameters of Eq. 4. Based on our experimental observations, both liquids glycerin and PDMS have finite value of spreading coefficient due to the finite value of Laplace pressure difference.

Adopting analogous reasoning, it is tempting to deduce that proper droplet spreading of PDMS would have ceased after a period of time not far off from the 250 seconds projected from Figure 5. Referring to Figure 4, the suggested end of PDMS droplet spreading as such would have occurred when the droplet height was in the range of a half millimeter. At this stage the contact angle was estimated to be 8 degrees using spherical cap approximation. Spreading beyond this stage must have assumed another mechanism, an issue that is being sought in the subsequent analysis.

Figure 4 Approximated droplet height is plotted against time for glycerin (solid line) and PDMS-1000 (dashed line) using spherical cap approximation for the first 100 seconds then using pancake approximation.

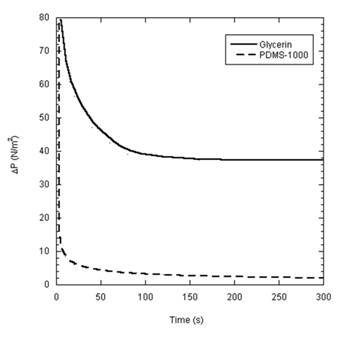
Figure 5 Pressure difference is plotted against time for glycerin (solid line) and PDMS-1000 (dashed line).

To further elucidate the dependence of the spreading kinetics on the pressure difference, the rates of change of both parameters are presented in Figure 6 as a function of the contact area for the glycerin droplet. The two rates, dP/dt and dA/dt, are mirror images of one another. As the rate of change in the pressure difference approaches zero, the rate of spreading also approaches zero. This match of the two rates is expectedly not unusual in the case of glycerin. Surprisingly, however, analysis of the PDMS data in the same fashion produces almost identical results (Figure 7). The rate of change in pressure approached zero at about 0.2cm² contact area. With no pressure in the droplet, this area must be the end of hydrodynamic spreading.

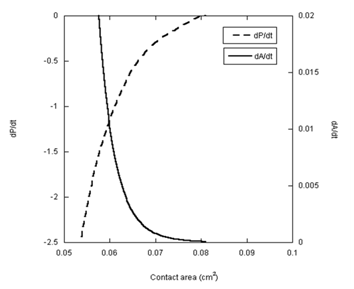
Figure 6 The rates of change the pressure difference (dP/dt) and the rate of spreading area (dA/dt) are plotted as a function of the contact area for the glycerin droplet.

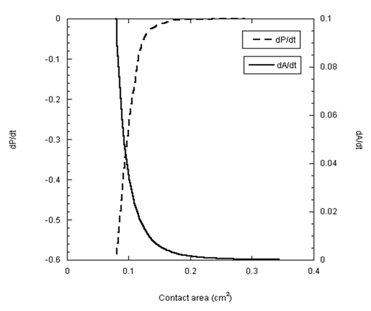
Figure 7 The rates of change the pressure difference (dP/dt) and the rate of spreading area (dA/dt) are plotted as a function of the contact area for PDMS-1000 droplet.

The findings presented above deeply questions the validity of “complete” spreading of PDMS. The evidence, so far, supports the notion that spreading is universally incomplete. To bring this argument to a satisfactory closure, an account for the mobility of PDMS beyond the spreading stage must be discerned.

Following the rapid decay of dA/dt (Figure 7) the rate of spreading appeared to decrease indefinitely. The trend of the data suggests that the transport of PDMS liquid ought to enter a Fickian-like regime. To verify this proposal the slow tail of the kinetic data are plotted in terms of a Fickian-type expression, i.e.,
$R_c=\sqrt{\frac{Dt}{\pi }}$                                               (5)
where the contact radius R_c of the film represents the length dimension and D is its diffusion coefficient.

As shown in Figure 8 the diffusion equation provides an excellent fit of the spreading data beyond 250 seconds. Attempts to incorporate earlier data (prior to 250 seconds) produced less satisfactory agreement with Eq. 5. The diffusion coefficient obtained from this analysis is 4.07x10^-10m²s^-1, a value which ascertains that the transport process in this stage was indeed of a Fickian character. The value of the diffusion coefficient obtained here falls within similar order of magnitude as that found for PDMS on silicon wafers using single-wavelength ellipsometry.¹⁴

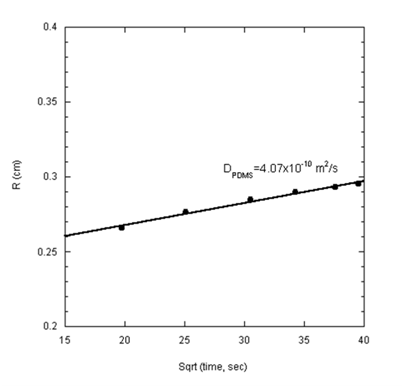
Figure 8 Contact radius versus the square root of time for PDMS-1000 spreading on glass substrate. The diffusion coefficient calculated is 4.07x10^-10 m²s^-1.

Noting that the spreading data of PDMS, beyond 250 seconds, are better described by Fickian kinetics and referring to Figure 4 & Figure 5, it becomes clear that a transition must have occurred when the droplet height reached 10’s micrometers and the Laplace pressure reached its plateau. It is generally upheld that diffusive transport in droplet spreading is an attribute of the first molecular layer of the liquid in contact with the solid substrate, i.e. the precursor film;^15,16 a phenomenon associated with Van der Waal interactions.^17,18

The above evidence indicates that the PDMS spreading ceased to move as a hydrodynamic system at about 250 seconds and gradually ensued diffusive transport.

The evidence presented above unambiguously supports the view that the spreading of PDMS-1000 droplet on soda-lime glass substrate took place through two distinct regimes. Like all other liquids, the droplet exhibited partial wetting assuming spherical cap geometry, driven by Laplace pressure for the first period of about 250 seconds. As Laplace pressure was depleted to its minimum, the droplet assumed an equilibrium contact angle of 8 degrees. At the end of the Laplace regime the film acquired a pancake-like structure whose thickness was in the range of few micrometers. This film was noted to spread by a diffusive mechanism, which lasted for a period of a few hours.

That PDMS uniquely undergoes a transition from Laplace flow to Fickian transport; seem to be associated with the well-known extraordinary molecular mobility of PDMS.

The present study analyzed the spreading kinetics of PDMS-1000 cp droplets on soda-lime glass, in comparison with glycerin. The so-called “complete” spreading of PDMS droplets could be resolved into two distinct regimes. The first was a flow regime, driven by Laplace energy and was believed to be resisted by the liquid/solid contact energy. It is therefore suggested that PDMS, like other liquids, experiences partial wetting with a finite contact angle of about 8 degrees. The second was a diffusive regime, driven by Fickian-type forces, which are thought to be associated with the extraordinary molecular mobility of PDMS.

None.

Authors declare there is no conflict of interest in publishing the article.

1. WA Zisman. J Paint Technology. 1972;44:41.
2. E Dussan, S Davis. On the motion of a fluid-fluid interface along a solid surface. J Fluid Mech. 1974;65(1):71−95.
3. VA Ogarev, TN Timonina, VV Arslanov, et al. Spreading of polydimethylsiloxane drops on solid horizontal surfaces. J Adhesion. 1974;6(4):337−355.
4. RL Hoffman. A study of the advancing interface. I. Interface shape in liquid-gas systems. J Colloid and Interface Science. 1975;50(2):228−241.
5. OV Voinov. Hydrodynamics of wetting. Fluid Dynamics. 1976;11(5);714−721.
6. LH Tanner. The spreading of silicone oil drops on horizontal surfaces. J Applied Physics. 1979;12(9):1473−1484.
7. PG de Gennes. Wetting: statics and dynamics. Review of Modern Physics. 1985;57(3);827−863.
8. A Seaver, J Berg. Spreading of a droplet on a solid surface. J Applied Polymer Science. 1994;52(3):431−435.
9. AM Alteraifi, D Sherif, A Moet. Interfacial effects in the spreading kinetics of liquid droplets on solid substrates. J Colloid and Interface Science. 2003;264(1):221−227.
10. AM Alteraifi, B Sasa. Spreading of liquid drops over solid substrates: 'like wets like'. Journal of Adhesion Science and Technology. 2006;20(12):1333−1343.
11. S Mitra, SK Mitra. Understanding the Early Regime of Drop Spreading. Langmuir. 2016;32(35):8843–8848.
12. MP Valignat, M Voue, G Oshanin, et al. Structure and dynamics of thin liquid films on solid substrates. Colloids and Surfaces A: Physicochemical and Engineering Aspects. 1999;154(1−2):25−31.
13. AM Alteraifi, A Hirbawi. Contact Ratio: A New Precise Measurement for Wettability. Canadian J of Chemical Engineering. 2006;84(1):33−38.
14. M Voue, MP Valignat, G Oshanin, et al. Dynamics of Spreading of Liquid Microdroplets on Substrates of Increasing Surface Energies. Langmuir. 1998;14(20):5951−5958.
15. JF Joanny, PG de Gennes. Upward creep of a wetting fluid: a scaling analysis. J Phys France. 1986;47:121–127.
16. F Heslot, AM Cazabat, P Levinson. Dynamics of wetting of tiny drops: Ellipsometric study of the late stages of spreading. Phys Rev Lett. 1989;62(11):1286.
17. J Lopez, CA Miller, EJ Ruckenstein. Spreading kinetics of liquid drops on solids. J Colloid Interface Sci. 1976;56(3):460–468.
18. E Perez, E Schaffer, U Steiner. Spreading Dynamics of Polydimethylsiloxane Drops: Crossover from Laplace to Van der Waals Spreading . J Colloid and Interface Sci. 2001;234(1):178−193.