
Review Article Volume 1 Issue 3
Simulation of the Propagation of Tsunamis in Coastal Regions by a Two-Dimensional Non-Hydrostatic Shallow Water Solver
Costanza Arico
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Department of Civil Engineering, University of Palermo, Italy
Correspondence: Costanza Arico, Department of Civil Engineering, Environmental, Aerospace, Materials, University of Palermo, Avenue of Sciences, 90128, Palermo, Italy
Received: November 14, 2017 | Published: November 27, 2017
Citation: Arico C (2017) Simulation of the Propagation of Tsunamis in Coastal Regions by a Two-Dimensional Non-Hydrostatic Shallow Water Solver. Fluid Mech Res Int 1(3): 00011. DOI: 10.15406/fmrij.2017.01.00011
Download PDF
Abstract
Due to the enormous damages and losses of human lives in the inundated regions, the simulation of the propagation of tsunamis in coastal areas has received an increasing interest of the researchers. We present a 2D depth-integrated, non-hydrostatic shallow waters solver to simulate the propagation of tsunamis, solitary waves and surges in coastal regions. We write the governing continuity and momentum equations in conservative form and discretize the domain with unstructured triangular Generalized Delaunay meshes. We apply a fractional-time-step procedure, where two problems (steps) are consecutively solved. In the first and in the second step, we hypothesize a hydrostatic and a non-hydrostatic distribution of the pressure, respectively. Several literature models, which solve the same set of equations, are based on a fractional-time-step procedure. In the hydrostatic step of these literature solvers, the flow field does not satisfy the depth-integrated continuity equation, since the momentum equations are solved independently of the continuity equation. In both steps of the proposed numerical scheme, the computed flow field satisfies the depth-integrated continuity equation discretized in each computational cell. This is obtained by solving together the governing equations, according to the different numerical procedures adopted in the steps of the algorithm. Wet/dry problems are implicitly embedded in the proposed numerical solver. We present several model applications where analytical or measured reference solutions are available. The computational effort required by the proposed procedure is investigated.
Keywords: Shallow waters; Non-hydrostatic pressure; Unstructured mesh; Wetting/drying; Tsunami propagation; Long waves; Voronoi cells; Runge-Kutta method; Galerkin scheme; Manning equation; Dirichlet condition; OpenFOAM
Abbrevations
BTMs: Boussinesq-Type Models; NLSWEs: Nonlinear Shallow Water Equations; FV: Finite Volumes; WD: Wetting/Drying; PDEs: Partial Differential Equations; DC: Diffusive Correction; MAST: Marching in Space and Time; CC: Convective Correction; GD: Generalized Delaunay; ODEs: Ordinary Differential Equations; CP: Convective Prediction
Introduction
During the last years, great effort has been addressed by several authors to simulate the propagation of solitary waves/tsunamis, tides or surges, due to the tremendous damages and losses of human lives in the inundated rural and residential areas. Tsunamis are sea waves usually generated by undersea landslides and earthquakes. They can be regarded as long/solitary waves with small amplitude and long wavelength, travelling with high speed over long distances. Approaching the coast, their amplitude increases, becoming potentially destructive. The propagation of tsunami in coastal regions can be studied by investigating the shoaling and breaking of solitary waves over inclined bottoms [1]. Chanson [2] asserted that the front of tsunamis over dry plains becomes a shock wave, and presented a similarity between the propagation of the tsunamis over dry coastal areas and the classical dam-break problems. Generally, 3D simulations of the processes described as above, e.g., by RANS models [3], or Smoothed Particle Hydrodynamics methods [4], or Volume of Fluids methods [5], require very high computational costs. For these reasons, a significant amount of literature based on depth-integrated equations has been published for simulations of long waves/tsunamis propagation. Generally, the two modeling approaches proposed in literature are the Boussinesq-Type Models (BTMs) and the Non-Hydrostatic Nonlinear Shallow Water Equations (NLSWEs) models.
The classical formulation of the BTMs [6] involves weak nonlinearity and dispersion. High-order BTMs have been proposed to overcome these difficulties, but suffer from complex numerical discretization, which leads to high computational efforts [7,8]. Generally, the BTMs also suffer from the inclusion, in the governing equations, of extra terms, based on empirical considerations, introduced for the simulation of wave breaking with the associated energy dissipation, and wetting/drying transition [8].
Hereafter, we call "hydrostatic NLSWEs" and "non-hydrostatic NLSWEs" (or "dynamic NLSWEs") respectively the NLSWEs with hydrostatic and non-hydrostatic (or dynamic) pressure distribution. Due to simplicity and accuracy, the hydrostatic NLSWEs, are largely applied for simulating wave processes in rivers, lakes, estuaries. The hydrostatic NLSWEs lack frequency dispersion and are not able in simulating some dispersive features of long waves/tsunamis propagation [8-13] as well as free-surface undulations at front/tail of bores and shock waves of tsunamis and dam-breaks [14,15]. Essentially two aspects allow reproducing the dispersive effects in the NLSWEs, 1) the decomposition of the pressure into its hydrostatic and dynamic components and 2) the inclusion of the vertical momentum equation in the governing equations [16]. Two fractional-step methodologies are usually applied to perform the decomposition of the pressure, the pressure projection and the pressure correction method, respectively [17].
One of the most demanding topics of the NLSWEs models is the simulation of the wave breaking [18]. As widely recognized, an accurate simulation of discontinuous flows (e.g., bores or jumps), is obtained if the numerical model solves the weak form of the hydrostatic NLSWEs written in conservative form [19-21]. Numerous shock-capturing procedures, in the framework of the Finite Volumes (FV), Finite Elements (FE) and Finite Differences (FD) schemes, have been proposed for the solution of the hydrostatic NLSWEs [22,23]. Only a few non-hydrostatic models are equipped with this shock-capturing feature [18,24,25].
In the NLSWEs applications involving fast transitions between wet and dry surfaces, e.g., coastal flooding and run-up of tsunamis, an accurate modeling of wetting/drying (WD) processes plays an important role. Several WD numerical techniques have been proposed [26-28], but generally these are affected by several drawbacks, e.g., the mass imbalance and the high computational costs due to additional relationships to include in the numerical procedure at the transition wet/dry surface [27].
In the present paper, we propose a non-hydrostatic NLSWEs solver to simulate the propagation of long waves, tsunamis and surges processes. We write the governing equations in conservative form and the total pressure is decomposed into its hydrostatic and dynamic components. A hydrostatic and a non-hydrostatic (or dynamic) problem (or step), consecutively solved, are embedded in a general fractional-time-step procedure. The domain is discretized with unstructured triangular Generalized Delaunay meshes [4]. Generally, the triangular meshes are suitable to fit irregular natural boundaries and arbitrary geometries. The hydrostatic step, where the dynamic pressure terms are neglected, is solved by a prediction-correction procedure, recently proposed in [30-33]. Unlike studies in [30-33], where a cell-centered formulation is applied, in the present solver we adopt a node-centered formulation.
We organize the paper as follows. We present the governing equations and the general formulation of the numerical solver in sections 2 and 3, respectively. The hydrostatic and dynamic steps are disentangled in sections 4 and 5, respectively, and the boundary conditions, in section 6. The properties of the proposed model (e.g. the proof of the local and global mass balance, the WD properties, the study of the phase speed, ... ) are outlined in section 7. Finally, in section 8, we present several model applications where reference analytical solutions or measured data are available. The proposed test cases highlight the skill of the model in simulating challenging features of the propagation of long, solitary waves and tsunami, as the wave breaking, run-up, and wetting/drying problems. In the same section we also investigate the computational burden.
The Governing Equations
We derive the governing equations from the continuity and Reynolds equations of an incompressible fluid (water),
(1),
(2),
where t is the time, u is the velocity vector (u, v, and w are its components along x, y and z directions, respectively), g is the gravitational acceleration vector,
, with g the norm of the gravitational acceleration (notation (*)T indicates the transposed of vector (*)),
is the density of the water, p is the pressure and
is the kinematic viscosity coefficient.
We assume a physical domain bounded along the vertical directions by the free surface H(x, y, t) and the bed surface (or bottom) zb(x, y, t), and h is the water depth (h = H - zb) (Figure 1). We operate under the hypothesis of fixed bed condition, i.e.,
, which implies
. The total derivatives of the bottom and free surfaces lead to the kinematic boundary conditions [34]
and
(3),
and the sub-indices b and s mark the values at the bottom and at the free surface, respectively. The (total) pressure p is split into its hydrostatic and dynamic components [16],
(4).

Figure 1: Definition sketch.
At z = H we set
, i.e., zero value of the atmospheric pressure.
If we integrate Eqs. (1)-(2) over the water depth h, from zb to H, we derive the depth-integrated NLSWEs [35]. If we merge Eqn (3) in the continuity equation, integrated along the water depth, it results
(5).
If we hypothesize that
changes linearly along z, from value 0 at z = H to value
at z = zb, dividing Eq. (2) by
, the depth-integrated momentum equations are
(6.a),
(6.b),
(6,c),
and the components of the depth-integrated velocity vector along x, y and z directionsare U, V and W, respectively, and the corresponding components of the specific flow rate vector (i.e. the flow rate per unitary width) are Uh, Vh and Wh,
and n is the Manning bed roughness coefficient. The Leibniz rule is applied to perform the integration along the depth of the terms proportional to qb [11,18]. We refer the reader to [36] for further details of the depth-integration of the governing equations. For brevity, we only explicit the terms in the x-momentum equation (6.a), and the terms in the other two momentum equations have similar meanings along the y and z directions, respectively. In x and y momentum equations (Eqs. (6.a)-(6.b)), we neglect the stress at the free surface (e.g., due to the action of the wind), and the depth-averaged turbulent/viscous stresses. Similarly to other studies [8,11,13,17,37,38], in Eq. (6.c), we neglect the vertical advection and dissipation terms compared with the dynamic pressure term, that is, we assume that the dynamic pressure is essentially due to the local time derivative of the vertical velocity of the water column.
The linear vertical variation of qb has been adopted by other authors [8,11,13,17,18,37,38] and it is consistent with the hypothesis of zero value of the atmospheric pressure. Following other authors, 8,11,13,17,18,37,38] we also hypothesize that the vertical component of the velocity changes linearly, from wb to ws, and its depth-integrated W value is
(7),
Both assumptions of the vertical distribution of qb and w require further investigation, but beyond the purpose of this paper. The unknown variables of the governing Partial Differential Equations (PDEs) (5)-(6) are h, Uh, Vh, Wh and qb.
General Features of the Numerical Algorithm
The fractional-time-step procedure
A fractional-time-step scheme, in the general framework of the pressure projection methods [17], is applied to solve the governing equations (5)-(6). The hydrostatic problem, in its turn, is solved applying a predictor-corrector scheme. If we neglect in Eqn. (6.a)-(6.b) the terms with the dynamic pressure, the hydrostatic NLSWEs become:
(8),
(9.a),
(9.b),
and the vertical momentum equation becomes trivial. The unknown variables of system (8)-(9) are h, Uh and Vh. In Appendix A we give more details of the predictor-corrector procedure applied for the solution of the hydrostatic problem (8)-(9). The functional characteristics of the prediction and correction steps of problem (8)-(9) are the ones of a convective and a diffusive process, respectively [31,32] (see also Appendix A). According to this, the prediction and correction systems are named "convective prediction" (CP0) and "diffusive correction" (DC) system, respectively. The original hyperbolic shallow waters problem is split into a convective plus a diffusive one.
We solve the hydrostatic CP0 problem using the A Marching in Space and Time (MAST) procedure [30,31,33], where the cells are ordered at the beginning of each time iteration, according to rules indicated as follows, and consecutively solved. Originally, MAST has been used for scalar potential flow fields (where the flow vector and the spatial gradient of the potential have opposite signs). To adopt this procedure in cases where a scalar potential of the flow field does not exist, as the present one (where the velocity vector is an unknown of the problem), a further convective correction step has been added [31,32]. The original hydrostatic CP0 step is split into a "convective prediction" (CP) and a "convective correction" (CC) step [31,32]. We use an auxiliary scalar function, the "approximated potential" for cells ordering (details in [31,32]).
In the hydrostatic DC step, a large linear system, whose dimension is equal to the number of the computational cells, is solved for the H unknowns, and the horizontal components of the flow rate are subsequently updated. In the dynamic problem of the general fractional-time-step scheme, we merge the terms of the momentum equations proportional to the non-hydrostatic pressure, as well as the boundary conditions at the free and bottom surfaces (Eqs. (3)), in the continuity equation (Eq. (1)), integrated over a computational cell. The resulting system is solved for the qb unknowns. Hence, the components of the flow rate are corrected, while the water level (depth) is not updated.
Others numerical schemes have been recently proposed for the solution of the non-hydrostatic NLSWEs, where a fractional-time-step procedure is applied [13,18,37,39]. In the hydrostatic step of these models, the flow field does not satisfy the depth-integrated continuity equation. This is why the momentum and the continuity equations are separately solved. Unlike these literature solvers, in both the hydrostatic and dynamic steps of the present scheme, the computed flow field satisfies the depth-integrated continuity equation discretized in each cell. As shown in sections 4 and 5, this is due 1) to the simultaneous solution of the continuity and momentum equations in the CP and CC steps, and 2) to the embedding of the momentum equations in the continuity equation in the hydrostatic DC and dynamic steps. As a result, the model preserves in all its steps the local and global mass balance, as shown in the following sections.
Computational mesh properties
To facilitate the reader, we briefly remind some basic concepts and nomenclatures of the unstructured triangular Generalized Delaunay (GD) meshes [29] adopted in the present study to discretize the domain.
is a 2D bounded domain and Th an unstructured triangulation of
. NTand N represent the total number of triangles and nodes (or vertices) of Th, respectively, and Te, e = 1, …, NT, is a generic triangle of Th, with area
is the edge vector connecting nodes i and ip, oriented from i to ip. Triangle Te shares side ri,ip with Tep,
is the distance with sign between the Tq circumcenter
(q = e, ep) and the midpoint of ri,ip, Pi,ip (Figure 2a) (see also Eqs. (19.b)-(19.b) in [29] and Eq. (B.1) in Appendix B), given by the cross product
(10),
where xi(ip), xi,ip and
are the vectors of the coordinates of i (ip), Pi,ip and
, respectively,
if the direction of ri,ip is counterclockwise in triangle Tq,
otherwise, and "x" is the symbol of the cross product. Eq. (B.2) in Appendix B represents the condition to be satisfied to guarantee the GD condition for side ri,ip.

Figure 2: a) Notations. b) The computational cell (dual finite volume, or Voronoi polygon). In bold black the boundary of the cell.
We construct a dual mesh over Th, where a dual finite volume ei, i =1, ..., N, is associated with node i. It is the Voronoi polygon, defined as in [40], shown in Figure 2b. We call the dual finite volumes, (computational) cells. A node-centered formulation is adopted, with the unknown variables stored in each node i. As motivated at the beginning of section 4.2 and in Appendix C, we concentrate the storage capacity in the nodes in the measure of 1/3 of the area of all the triangles sharing the node.
We will prove that the GD mesh property ensures that 1) the sign of the flux among contiguous cells only depends on the flow rate vector, in the CP and CC hydrostatic steps (in section 4.1), 2) the M-property of the matrix of the systems in the DC hydrostatic step and in the dynamic problem, respectively (in sections 4.2 and 5), and, 3) the sign of the flux among contiguous cells are consistent with the differences of the values of H and qb in the same cells, respectively, in the DC hydrostatic step and in the non-hydrostatic problem (in sections 4.2 and 5). See for example in [41] the definition of a M-matrix.
Let Suppi be the support of cell i, i.e., the set of the NT,i triangles sharing node i. Ai and Nli denote the area and the number of the sides of the boundary of the cell associated to node i, respectively. Ai is computed as
r = 1, ..., NT,i (11).
Hereafter we assume that cell i shares its lth side (l = 1, ..., Nli) with cell ip (Figure 2b). Length with sign dl,i of side l is given by (Figure 2a)
with
(12),
with
defined in Eq. (10) and Eq. (B.1) in Appendix B. According to the definition of
, side l is orthogonal to ri,ip. From Eqs. (10), (12) and (B.1) in Appendix B, dl,i could be either positive, either negative. In a GD mesh, dl,i is always positive (see Eq. (10) and Appendix B). The boundary of the cell i is defined as
, always positive in a GD mesh.
The Hydrostatic Problem
Eqs. (8)-(9) are integrated in space (see also Eqs. (A.3)-(A.5) in Appendix A), and, using the Green’s theorem, we get the integral formulation
i = 1, …, N (13),
s = x, y (14.a),
(14.b),
where sub index i marks the variables in cell i, Fl,i and
, further specified, are the flux and the x(y) component of the momentum flux across side l (l = 1, ..., Nli) of cell i and
is the source term. The Manning coefficient in cell i, ni is computed as the mean value of the friction coefficients in the triangles sharing node i. The spatial gradients of the water level are kept constant in the prediction step of the hydrostatic problem (see Eq (14,b)), as motivated in [31,32].
In accordance to the formulation in Eqs. (A.3)-(A.5) in Appendix A, the linearized differential formulation of the DC problem is
(15),
(16),
and the symbol (
) marks the mean-in-time value of the variable (*). The initial states of the CC and DC steps are the solutions of the CP and CC steps, respectively. In Eqs. (16) we assume negligible the difference between the sum of the convective terms and the mean-in-time values of the same quantities obtained after the (CP + CC) steps [31,32]. Symbols (*)k, (*)k+1/3, (*)k+2/3, (
mark the values of the variable (*) at the beginning of the time iteration, at the end of the convective prediction, convective correction and diffusive correction steps, respectively.
In the prediction steps, we assume, inside each computational cell, piecewise constant values of h, Uh, Vh. The correction system (15)-(16) is solved applying a technique similar to the linear (P1) conforming FE Galerkin scheme (see section 4.2). The procedure for the solution of the hydrostatic problem has been proposed in [32], where we adopted a cell-centered formulation with storage capacity concentrated in the mesh triangles. The node-centered formulation with respect to the Voronoi cells, presented in this paper, leads to a different spatial discretization of the governing equations. In the following sections 4.1 and 4.2, we only report the steps of the numerical formulation of the hydrostatic problem involved in the new spatial discretization. In test 3 (section 8.3) we compare the efficiency and accuracy of the two formulations using an analytical reference solution.
The prediction problem
All the computational cells, at the beginning of each time iteration, are ordered according to the value of the approximated potential
, known inside each cell, and computed according to the procedure proposed in [31,32]. This procedure, at the beginning of the time step, minimizes the differences [31,32]. From Eq. (12), we set the flux FLl,i through side l as
(17),
where
is the unit vector parallel to side ri,ip (i.e., orthogonal to side l) positive outwards from i, i.e., oriented from i to ip, qi is the specific horizontal flow rate vector in cell i, qi = ((Uh)i, (Vh)i)T. and symbol
marks the dot product. Eq. (17) becomes
(18).
If the GD property holds for side ri,ip, dl,i is positive (see Eq. (10) and Appendix B), and the sign of FLl,i only depends on the dot product
, and a leaving (incoming) flux from (in) cell i is positive (negative). This condition is not fulfilled if the GD property is not satisfied, since dl,i is negative. The fluxes and momentum fluxes between cells i and ip in Eqs. (13)-(14) are defined as
if (
and
)
otherwise (19),
if
,
otherwise (20),
where m is the side of cell ip shared with cell i. Eqs. (19)-(20) guarantee the continuity of the flux and the momentum flux at each internal cell side, so that
and
. For an external boundary side, the condition Fl,i = Fll,i holds for an outward oriented (positive) flux.
Thanks to the consecutive solution of the cells performed in the MAST procedure, the system of PDEs (13)-(14) for each cell i are written as a system of Ordinary Differential Equations (ODEs) (more details in [31-33]). After the cells ordering, in the CP step we proceed from the cell with the highest to the cell with the lowest value of
, and solve a ODEs system for each cell in the interval
(from time level tk to time level tk+1/3and
is the size of the time step). After that, in the CC step, we proceed from the cell with the lowest to the cell with the highest value of
, solving an ODEs system in each cell in the interval
(from time level tk+1/3 to time level tk+2/3).
A 5th order Runge-Kutta method with adaptive stepsize control [42] is applied for the solution of the ODEs system. The ODEs system for the CP step is
(21),
s = x, y (22),
with
defined in Eqs. (14,b),
if flux across side l is oriented outward i , 0 otherwise and
, if
(23.a),
, if
(23.b).
The right hand side (r.h.s.) of Eqs. (21)-(22) are the mean-in-time values of the incoming flux and x/y momentum fluxes, respectively, known after the solution of the linked ip cells with higher value of
, solved before i [31,32]. The gradients of H in the Rx(y) term are computed as proposed in 4.3.
Once the ODEs (21)-(22) are solved for cell i, the mean-in-time value of the total flux
leaving from i, is given by the local mass balance [32],
(24),
where
(i.e., the r.h.s. of Eq. (21)). Following [32], we compute the mean-in-time value of the flux
leaving from side l of i to the neighboring cell ip with
, by partitioning
on the base of the ratio between the flux
and the sum of all the leaving fluxes to the neighboring cells at the end of the time step,
(25.a),
and we estimate in a similar way the mean-in-time values of the leaving momentum flux
. Finally, we set:
(25.b),
for all the neighboring ip cells with
and we proceed to solve system (21)-(22) for the ip cells among the unsolved ones. A similar algorithm is applied to solve the convective correction step, whose ODEs system for the generic cell i is
(26),
s = x, y (27),
with
s = x, y if
(28,a),
and
if
(28,b).
The source terms is allocated in the convective prediction step [32]. The initial state in each cell of the convective correction step is the one computed in the same cell at the end of the convective prediction step. After the ODEs system (26)-(27) is solved in cell i, the mean-in-time value of the flux/momentum flux leaving from side l of i to the neighboring cell ip with
, from tk+1/3 to tk+2/3, is computed similarly to the previous CP step. Further comments concerning the MAST procedure can be found in [31,32].
The mean-in-time values
and
, required for the DC step (see Eqs. (16)), are obtained by numerical integration during the solution of each ODEs system during the convective prediction and correction steps [31,32].
The diffusive correction problem
After the prediction components of the water depths (levels) are computed with piecewise constant approximation (P0) inside each cell, a continuous piecewise linear (P1) shape is assigned to the water depths (levels) computed at the end of the (CP + CC) steps, obtained from the nodal values. If we move from the P0 to the P1 approximation, at a given time level, we do not alter the estimation of the global mass, if the polygons of the P0 approximation (Figure 2b) are the same as the ones of the P1 approximation. If we use, for the solution of the DC problem the conforming P1 Galerkin FE scheme, where the polygons are delimited by the centers of mass (see Appendix C), we introduce a small mass balance error. We avoid this error, using the same polygons for the P0 and P1 approximations. Other details in Appendix C.
We use a fully implicit time discretization of the DC problem (15)-(16) [32]. Under the hypothesis of fixed bed condition, we get the following differential equation for the generic cell i
(29),
s = x, y (30),
where
. From Eq. (30), the flow rate components at the end of the hydrostatic step are
s = x, y (31),
with coefficients
and
defined as
s = x, y (32).
We merge Eqs. (31) in Eq. (29) and, after space integration and application of the Green's theorem, we get the following balance law for cell i
(33),
where
is the water level gradient along the
direction and the other symbols are specified as above. Concerning the second term on the r.h.s. of Eq. (33), we have
(34),
while
is computed after the (CP + CC) steps. After discretization in time, Eq. (33) becomes
i = 1, ..., N (35),
where
is the corrective flux across side l of cell i
(36.a),
and the term
on the r.h.s. of Eq. (35) is
(36.b).
Due to the P1 spatial approximation,
only depends on the values at nodes i and ip (since
is parallel to ri,ip and orthogonal to side l, see sections 3.2 and 4.1), and
is written
(37).
Eqs. (35) constitute a linear system of order N in the Hi (i = 1, …, N) unknowns, whose matrix is sparse and symmetric. Generally the non-zero entries are about 5% or less of the total number of matrix coefficients. The diagonal and off-diagonal matrix coefficients are, respectively
i, ip = 1, ..., N (38),
where
if nodes i and ip are linked, otherwise it is equal to zero.
According to Eqs. (37)-(38), the off-diagonal coefficients are non-negative if the GD mesh property is not satisfied for side ri,ip and the M-matrix property is lost. In this case, dl,i is negative (see Eq. (10) and Appendix B) and the sign of
is not consistent with the difference
in Eq. (37). On the opposite, if side ri,ip satisfies the GD property, dl,i is positive, and the sign of the flux in Eq. (37) only depends on the difference of the water levels in cells i and ip. If the GD property is satisfied for all the sides of the mesh, the matrix of system (35) is a M-matrix, positive-definite and, according to [41], the system is well-conditioned.
The numerical scheme adopted for the solution of the DC problem has a structure similar to the P1 conforming FE Galerkin scheme, and we present and discuss analogies and differences between the two numerical formulations in Appendix C.
We solve system (35) by a preconditioned conjugate gradient method (with incomplete Cholesky preconditioning). Due to the symmetry of the matrix of system (35), we only save the non-zero entries of the lower triangular matrix, using a Symmetric Coordinate Storage algorithm [43 ].
After the solution of system (35) for the H unknowns, we compute the gradients of the water level
at the end of the DC step as shown in the next section. As specified in section 4.1, the values of the gradients of the water level are assumed constant during the solution of the two convective steps of the hydrostatic problem in the next time iteration [31,32]. Finally, the components of the flow rate
(s = x, y) are updated according to Eqs. (31)-(32).
According to Eq. (37) and the definition of the coefficient
in (Eq. (32)), the flux
leaving from cell i (ip) to ip (i) is equal to the flux entering cell ip (i) from cell i (ip). If
is leaving from i to ip or vice versa depends on the difference
(see Eq. (37).
Computation of the spatial gradients of the water level
We compute the gradient of H in cell i as follows. Call
the unit vector parallel to the flow vector in cell i. Let
be the vector computed as (ip is one of the cells linked with i),
(39).
We assume
(40),
where
is the dot product between the direction of side ri,ip and the unitary flow rate vector. If cell i lies on an impervious boundary, the flow rate vector is parallel to the boundary and
, computed as in Eq. (40), is projected along the boundary direction.
The expression in Eq. (40) can be regarded as an upwind formulation, where
depends on the differences between Hi and the values of H in the downstream (along the flow direction) ip cells. This is consistent with the procedure adopted in the (CP + CC) steps, where the unknown fluxes/momentum fluxes are the ones leaving from i to the downstream ip cells.
The Hydrostatic Problem
Eqs. (8)-(9) are integrated in space (see also Eqs. (A.3)-(A.5) in Appendix A), and, using the Green’s theorem, we get the integral formulation
i = 1, …, N (13),
s = x, y (14.a),
(14.b),
where sub index i marks the variables in cell i, Fl,i and
, further specified, are the flux and the x(y) component of the momentum flux across side l (l = 1, ..., Nli) of cell i and
is the source term. The Manning coefficient in cell i, ni is computed as the mean value of the friction coefficients in the triangles sharing node i. The spatial gradients of the water level are kept constant in the prediction step of the hydrostatic problem (see Eq (14,b)), as motivated in [31,32].
In accordance to the formulation in Eqs. (A.3)-(A.5) in Appendix A, the linearized differential formulation of the DC problem is
(15),
(16),
and the symbol (
) marks the mean-in-time value of the variable (*). The initial states of the CC and DC steps are the solutions of the CP and CC steps, respectively. In Eqs. (16) we assume negligible the difference between the sum of the convective terms and the mean-in-time values of the same quantities obtained after the (CP + CC) steps [31,32]. Symbols (*)k, (*)k+1/3, (*)k+2/3, (
mark the values of the variable (*) at the beginning of the time iteration, at the end of the convective prediction, convective correction and diffusive correction steps, respectively.
In the prediction steps, we assume, inside each computational cell, piecewise constant values of h, Uh, Vh. The correction system (15)-(16) is solved applying a technique similar to the linear (P1) conforming FE Galerkin scheme (see section 4.2). The procedure for the solution of the hydrostatic problem has been proposed in [32], where we adopted a cell-centered formulation with storage capacity concentrated in the mesh triangles. The node-centered formulation with respect to the Voronoi cells, presented in this paper, leads to a different spatial discretization of the governing equations. In the following sections 4.1 and 4.2, we only report the steps of the numerical formulation of the hydrostatic problem involved in the new spatial discretization. In test 3 (section 8.3) we compare the efficiency and accuracy of the two formulations using an analytical reference solution.
The prediction problem
All the computational cells, at the beginning of each time iteration, are ordered according to the value of the approximated potential
, known inside each cell, and computed according to the procedure proposed in [31,32]. This procedure, at the beginning of the time step, minimizes the differences [31,32]. From Eq. (12), we set the flux FLl,i through side l as
(17),
where
is the unit vector parallel to side ri,ip (i.e., orthogonal to side l) positive outwards from i, i.e., oriented from i to ip, qi is the specific horizontal flow rate vector in cell i, qi = ((Uh)i, (Vh)i)T. and symbol
marks the dot product. Eq. (17) becomes
(18).
If the GD property holds for side ri,ip, dl,i is positive (see Eq. (10) and Appendix B), and the sign of FLl,i only depends on the dot product
, and a leaving (incoming) flux from (in) cell i is positive (negative). This condition is not fulfilled if the GD property is not satisfied, since dl,i is negative. The fluxes and momentum fluxes between cells i and ip in Eqs. (13)-(14) are defined as
if (
and
)
otherwise (19),
if
,
otherwise (20),
where m is the side of cell ip shared with cell i. Eqs. (19)-(20) guarantee the continuity of the flux and the momentum flux at each internal cell side, so that
and
. For an external boundary side, the condition Fl,i = Fll,i holds for an outward oriented (positive) flux.
Thanks to the consecutive solution of the cells performed in the MAST procedure, the system of PDEs (13)-(14) for each cell i are written as a system of Ordinary Differential Equations (ODEs) (more details in [31-33]). After the cells ordering, in the CP step we proceed from the cell with the highest to the cell with the lowest value of
, and solve a ODEs system for each cell in the interval
(from time level tk to time level tk+1/3and
is the size of the time step). After that, in the CC step, we proceed from the cell with the lowest to the cell with the highest value of
, solving an ODEs system in each cell in the interval
(from time level tk+1/3 to time level tk+2/3).
A 5th order Runge-Kutta method with adaptive stepsize control [42] is applied for the solution of the ODEs system. The ODEs system for the CP step is
(21),
s = x, y (22),
with
defined in Eqs. (14,b),
if flux across side l is oriented outward i , 0 otherwise and
, if
(23.a),
, if
(23.b).
The right hand side (r.h.s.) of Eqs. (21)-(22) are the mean-in-time values of the incoming flux and x/y momentum fluxes, respectively, known after the solution of the linked ip cells with higher value of
, solved before i [31,32]. The gradients of H in the Rx(y) term are computed as proposed in 4.3.
Once the ODEs (21)-(22) are solved for cell i, the mean-in-time value of the total flux
leaving from i, is given by the local mass balance [32],
(24),
where
(i.e., the r.h.s. of Eq. (21)). Following [32], we compute the mean-in-time value of the flux
leaving from side l of i to the neighboring cell ip with
, by partitioning
on the base of the ratio between the flux
and the sum of all the leaving fluxes to the neighboring cells at the end of the time step,
(25.a),
and we estimate in a similar way the mean-in-time values of the leaving momentum flux
. Finally, we set:
(25.b),
for all the neighboring ip cells with
and we proceed to solve system (21)-(22) for the ip cells among the unsolved ones. A similar algorithm is applied to solve the convective correction step, whose ODEs system for the generic cell i is
(26),
s = x, y (27),
with
s = x, y if
(28,a),
and
if
(28,b).
The source terms is allocated in the convective prediction step [32]. The initial state in each cell of the convective correction step is the one computed in the same cell at the end of the convective prediction step. After the ODEs system (26)-(27) is solved in cell i, the mean-in-time value of the flux/momentum flux leaving from side l of i to the neighboring cell ip with
, from tk+1/3 to tk+2/3, is computed similarly to the previous CP step. Further comments concerning the MAST procedure can be found in [31,32].
The mean-in-time values
and
, required for the DC step (see Eqs. (16)), are obtained by numerical integration during the solution of each ODEs system during the convective prediction and correction steps [31,32].
The diffusive correction problem
After the prediction components of the water depths (levels) are computed with piecewise constant approximation (P0) inside each cell, a continuous piecewise linear (P1) shape is assigned to the water depths (levels) computed at the end of the (CP + CC) steps, obtained from the nodal values. If we move from the P0 to the P1 approximation, at a given time level, we do not alter the estimation of the global mass, if the polygons of the P0 approximation (Figure 2b) are the same as the ones of the P1 approximation. If we use, for the solution of the DC problem the conforming P1 Galerkin FE scheme, where the polygons are delimited by the centers of mass (see Appendix C), we introduce a small mass balance error. We avoid this error, using the same polygons for the P0 and P1 approximations. Other details in Appendix C.
We use a fully implicit time discretization of the DC problem (15)-(16) [32]. Under the hypothesis of fixed bed condition, we get the following differential equation for the generic cell i
(29),
s = x, y (30),
where
. From Eq. (30), the flow rate components at the end of the hydrostatic step are
s = x, y (31),
with coefficients
and
defined as
s = x, y (32).
We merge Eqs. (31) in Eq. (29) and, after space integration and application of the Green's theorem, we get the following balance law for cell i
(33),
where
is the water level gradient along the
direction and the other symbols are specified as above. Concerning the second term on the r.h.s. of Eq. (33), we have
(34),
while
is computed after the (CP + CC) steps. After discretization in time, Eq. (33) becomes
i = 1, ..., N (35),
where
is the corrective flux across side l of cell i
(36.a),
and the term
on the r.h.s. of Eq. (35) is
(36.b).
Due to the P1 spatial approximation,
only depends on the values at nodes i and ip (since
is parallel to ri,ip and orthogonal to side l, see sections 3.2 and 4.1), and
is written
(37).
Eqs. (35) constitute a linear system of order N in the Hi (i = 1, …, N) unknowns, whose matrix is sparse and symmetric. Generally the non-zero entries are about 5% or less of the total number of matrix coefficients. The diagonal and off-diagonal matrix coefficients are, respectively
i, ip = 1, ..., N (38),
where
if nodes i and ip are linked, otherwise it is equal to zero.
According to Eqs. (37)-(38), the off-diagonal coefficients are non-negative if the GD mesh property is not satisfied for side ri,ip and the M-matrix property is lost. In this case, dl,i is negative (see Eq. (10) and Appendix B) and the sign of
is not consistent with the difference
in Eq. (37). On the opposite, if side ri,ip satisfies the GD property, dl,i is positive, and the sign of the flux in Eq. (37) only depends on the difference of the water levels in cells i and ip. If the GD property is satisfied for all the sides of the mesh, the matrix of system (35) is a M-matrix, positive-definite and, according to [41], the system is well-conditioned.
The numerical scheme adopted for the solution of the DC problem has a structure similar to the P1 conforming FE Galerkin scheme, and we present and discuss analogies and differences between the two numerical formulations in Appendix C.
We solve system (35) by a preconditioned conjugate gradient method (with incomplete Cholesky preconditioning). Due to the symmetry of the matrix of system (35), we only save the non-zero entries of the lower triangular matrix, using a Symmetric Coordinate Storage algorithm [43 ].
After the solution of system (35) for the H unknowns, we compute the gradients of the water level
at the end of the DC step as shown in the next section. As specified in section 4.1, the values of the gradients of the water level are assumed constant during the solution of the two convective steps of the hydrostatic problem in the next time iteration [31,32]. Finally, the components of the flow rate
(s = x, y) are updated according to Eqs. (31)-(32).
According to Eq. (37) and the definition of the coefficient
in (Eq. (32)), the flux
leaving from cell i (ip) to ip (i) is equal to the flux entering cell ip (i) from cell i (ip). If
is leaving from i to ip or vice versa depends on the difference
(see Eq. (37).
Computation of the spatial gradients of the water level
We compute the gradient of H in cell i as follows. Call
the unit vector parallel to the flow vector in cell i. Let
be the vector computed as (ip is one of the cells linked with i),
(39).
We assume
(40),
where
is the dot product between the direction of side ri,ip and the unitary flow rate vector. If cell i lies on an impervious boundary, the flow rate vector is parallel to the boundary and
, computed as in Eq. (40), is projected along the boundary direction.
The expression in Eq. (40) can be regarded as an upwind formulation, where
depends on the differences between Hi and the values of H in the downstream (along the flow direction) ip cells. This is consistent with the procedure adopted in the (CP + CC) steps, where the unknown fluxes/momentum fluxes are the ones leaving from i to the downstream ip cells.
The Non-Hydrostatic Problem
The divergence-free continuity Eq. (1) is integrated to the control volume
corresponding to the computational cell i,
and, due to the divergence theorem, we obtain the following balance relation between the horizontal and the vertical fluxes,
(41.a),
where
is the vertical surface of
(
with
defined in section 3.2), Uh = (U, V)T and
is the unitary vector perpendicular to
, positive outward. Eq. (41.a) can be written as
(41.b).
Let
be the first term on the left hand side (l.h.s.) of Eq. (41.b), with
the flux across the l-th side of
, computed by Eq. (18) at the end of the hydrostatic DC step (with
, s = x, y).
According to Eq. (7), the z momentum equation (Eq. (6.c)) becomes
(42).
After discretization in time, we approximate Eq. (42) as
(43),
the bottom vertical velocity as (see the first of Eqs. (3))
(44),
and the vertical velocity at the free surface is computed by Eq. (43), as
(45).
The horizontal, dynamic components of the momentum equations are
s = x, y (46).
After discretization in time, Eqs. (46) become
(47).
Symbol (
)k+1 marks the values of the variables at the end of the non-hydrostatic step.
Substituting Eqs. (44)-(45) and Eqs. (47) in Eq. (41,b), using the previous symbols, we get the following equation in the qb unknown
i = 1, ..., N (48),
where
(49),
and
is the qb gradient along the
direction. We set
(50),
and it can be considered a (corrective) flux due to the difference of qb in cell i and in the neighboring ip one (its units are cubic meters per seconds, i.e., the ones of a volumetric flux).
As for the hydrostatic DC step, we adopt a linear P1 spatial approximation of the qb unknowns according to the nodal values, and the computational cell is the same as in the hydrostatic problem.
Similar to Eq. (37), we rewrite Eq. (50) as
(51).
As in the DC problem, if the GD property is satisfied for side ri,ip, dl,i is positive (see Eq. (10) and Appendix B), and the sign of
only depends on the difference of qb in the two cells i and ip, while the opposite occurs if the GD property is not satisfied.
Eqs. (48) form a linear system of order N in the qb,i (i = 1, …, N) unknowns. The diagonal and off-diagonal entries of the matrix are, respectively
i, ip = 1, ..., N (52),
where
and
are the spatial gradients of H and zb computed along the direction
. The gradient of zb in cell i are computed as the gradient of H (see section 4.3). The other symbols are specified as above. The source term of system (48) is
(53).
Once qb is computed in each cell i, the horizontal flow rate components are updated according to Eqs. (47) and the velocity of the free surface according to Eq. (45).
Similarly to the DC step (section 4.2), the matrix of system (48) is sparse, symmetric and, for a GD mesh, positive-definite, and system (48) is solved as system (35) (see section 4.2).
As for the corrective flux
in the hydrostatic DC step, according to Eq. (51) and the definition of the coefficient
in (Eq. (49)), the flux
leaving from cell i (ip) to ip (i) is equal to the flux entering cell ip (i) from cell i (ip). If
is leaving from i to ip or vice versa depends on the difference
(see Eq. (51)).
Boundary Conditions (B.C.)
As specified in section 3, at the free surface, the stress of the wind is neglected and the (atmospheric) pressure is set to zero. The friction at the bottom is approximated by the Manning equation, (see Eqs. (6.a)-(6.b)). We assign free slip condition at the impervious walls.
During the CP hydrostatic problem, we deal with the B.C. for those cells with incoming and leaving flux/momentum fluxes as in section 4.4 of [33] (for brevity we refer the reader to the mentioned paper). The external assigned incoming fluxes/momentum fluxes are considered in the CP step [31,33]. During the CC step, in the inlet/outlet cells, we set the incoming fluxes and momentum fluxes from the neighboring cells equal to the leaving ones. This means that, in the boundary cells, the solution of the convection prediction problem is not altered by the convection correction problem. The B.C. in the DC step is handled as in [33]. We set qb = 0 in the inlet and outlet cells and this represents a Dirichlet condition for the solution of system (48).
Model Properties
Preservation of the local and global mass balance
The hydrostatic and dynamic problems involved in the proposed procedure rely on the local mass balance. This is imposed, for each cell i, after the solution of the ODEs system of the governing equations in the CP and CC steps (see Eq. (24)). The systems solved in the hydrostatic DC and dynamic steps are derived by a local mass balance, obtained by embedding the momentum equations in the continuity equation (see Eqs. (33)-(34) for the DC step and Eqs. (41) and (48) for the dynamic problem). We show that the proposed solver also preserves the global mass balance in all its steps.
Summing all Eqs. (24) at the end of the CP problem, we get
(54),
and, due to Eq. (25,b), for each internal couple of linked cells i and ip, the r.h.s. of Eq. (54) is equal to the difference between the boundary incoming and leaving fluxes. i.e.,
(55,a),
with
and
the sum of the incoming (assigned) and leaving boundary fluxes. In a similar way, at the end of the CC step, due to the continuity of the mean-in-time flux between i and ip (similarly to Eq. (25.b)) and since we handle the assigned boundary incoming fluxes
in the CP step (see section 6), after simple manipulations, we can easily show that
(55.b),
where
is the sum of the leaving boundary flux computed at the end of the CC problem. In the hydrostatic DC problem, as specified at the end of section 4.2, the flux
leaving from cell i (ip) to ip (i) is equal to the flux entering cell ip (i) from cell i (ip). This implies that the sum of all these fluxes is zero and, after simple manipulations, it can be show that
(55.c),
with Fdir the sum of the boundary fluxes computed at the cells with imposed Dirichlet conditions.
If we add Eq. (55,c) to Eq. (55,b), we obtain
(55.d),
which can be assumed as a relationships representing the global mass balance at the end of the hydrostatic problem. Because for each couple of linked internal cells i and ip, the corrective dynamic flux
leaving from i (ip) to ip (i) (in Eq. (51)) is equal to the flux entering ip (i) from i (ip) (see also the consideration at the end of section 5), the sum of all these internal fluxes is zero. On the other hand, the corrective boundary flux of the cells at the boundaries is zero, since we set qb = 0 as boundary Dirichlet assigned value (see section 6). This means that the non-hydrostatic step does not affect the global mass balances.
Preservation of a general steady gtate (GSS) condition
We assume that the GSS condition is achieved if the two relationships in Eq. (56) hold in each cell:
and
s = x, y i = 1, ..., N (56).
The numerical procedure proposed for the solution of the (CP + CC) steps for a generic cell relies on (see sections 4 and 5): 1) the balance of the incoming and leaving fluxes with the time change of the storage term, for the continuity equation and, 2) the balance among the incoming and leaving momentum fluxes with the time change of the flow rates, with the resultant of the hydrostatic pressure distribution, along cell interfaces and bottom surfaces, and the resultant of the bottom friction term, for the momentum equations.
Given an initial condition in the domain, hi, and qs,i, i = 1, ..., N and s = x, y, the above considerations imply the two following conditions,
a) If the incoming fluxes in any cell i are equal to the leaving ones, then h does not change in time, i.e., from Eqs. (21) and (26),
with symbol r = p, c (57),
b) If the incoming and leaving momentum fluxes in any cell i are balanced by the resultant of the hydrostatic pressure distribution along the cell interfaces and bottom surfaces, as well as by the resultant of the bottom stress term, then the specific flow rates in cell i do not change in time, i.e., from Eqs. (22) and (27),
(58),
with
in the CP step,
in the CC step. Apex r in Eqs. (57)-(58) is equal to "p" (in the convective prediction step) or "c" (in the convective correction step) and in this second case the source term Ri is equal to zero (see section 4.1).
Moreover, due to the fixed bed assumption, if the water depths in all the i cells do not change in time, neither the water levels nor their spatial gradients will do. We will show that, if conditions a) and b) of the (CP + CC) steps hold, the hydrostatic DC step and the dynamic problem do not modify this steady state condition for each cell. If the flow rate components do not change in time during the (CP + CC) steps (condition b) holds), the second sum on the r.h.s. of Eq. (33) in the DC step is zero, and, after simple manipulations, the same equation can be written as:
(59),
with
and
. If h (H) in all the i cells does not change in time during the (CP + CC) steps (condition a) holds),
is zero, and the solution of Eq. (59) is identically
, i.e., zero water level correction. From Eq. (31) we get that the correction of the specific flow rate components after the DC step is zero. In brief, if conditions a) and b) hold, we get:
c)
for each cell i,
d)
, s = x, y for each cell i.
We prove that the correction due to the non-hydrostatic problem is zero as well. We focus our attention on the r.h.s. of Eq. (48). We find the two following conditions e) and f),
e) If conditions b) and d) hold, the sum of the horizontal fluxes is zero for any i cell, i.e.,
,
f) If conditions a) to d) hold,
(s = x, y).
From condition-(f) and Eqs. (3), we obtain that
. Integrating the divergence-free continuity equation (Eq. (1)) to a control volume corresponding to the generic computational cell (see section 5), From condition e) we get
.
According to these considerations, the r.h.s. of Eqs. (48) is zero and this leads to qb = 0. This implies that the dynamic correction of the flow rate components, with respect to the initial condition, is zero and it is consistent with the second condition in Eq. (54).
The "water at rest" condition [44] is a particular case of the general situation described as above, where the flow rate components qs,i (s = x, y) are zero for all the i cells. In this case, according to the argumentations as above, it easy to prove the C-property of the present model [44].
Handling of wetting/drying processes
In [32] the authors show 1) how negative water depths do not arise during the solution of the (CP + CC) steps and 2) how to handle small negative values of water depth calculated after the solution of the linear system of the DC step. If, after the solution of the hydrostatic step, we have, in cell i,
, we set qb = 0, as Dirichlet value in system (48).
Study of the frequency dispersion
We compare the phase speed of the proposed model with the one given by the linear wave theory. The phase speed from the linear wave theory is [34]:
(60.a)
where kw is the wave number (
is the wave length). The wave period Tw is equal to Lw/c1. We assume a standing regular wave with Lw = 20 m in a closed basin, 40 m long (= 2 Lw) and 1 m wide, with frictionless and horizontal bottom. The wave profile is:
(60,b),
where
is the distance between the still water level and the free surface and aw is the wave amplitude. We keep constant the value for aw, equal to 0.1 m and h ranges from 1 m to 20 m. This experiment is similar to the one performed in [11,16,18], where the authors assumed a channel length equal to Lw /2. We discretize the domain with equilateral triangles with side 0.1 m. The wave period is divided in 160 parts and the total simulation time is 30 Tw. We registered the computed
elevation at two gauges, placed along the centerline of the channel, far Lw /2 and 3/2 Lw from the upstream end, so that the distance between the two gauges is equal to the wave length. We compute the numerical phase speed cn = Lw/Tw,n, where Tw,n is the time measured between two consecutive wave peaks of the same gauge, the first in the exact
profile, the second in the computed
profile (Figure 3.a). In Figure 3.b we compare the numerical and the linear wave theory phase speeds versus kh, and we also plot the phase celerity analytically computed for the shallow waters limit (e.g., c = (gh)1/2. The numerical phase speed plotted in Figure 3.b is obtained as the mean value between the phases speed computed for the two gauges, which have very similar values. The numerical phase celerity begins to deviate from the linear theory at about kh = 2.74, i.e., for h/Lw = 0.436, corresponding to the "intermediate waters" [34]), similarly to the weakly dispersive BTMs [11,45]. Setting Tw,n as the time interval between two consecutive wave peaks computed at gauges G1 and G2, we obtained results very similar to the ones in Figure 3.b. A small increment of cn has been computed between kh = 4 - 5 (Figure 3.b). According to the numerical results, in this interval, the numerical solution progressively deviates from the linear theory, and a slight increment of the phase speed is balanced by a reduction of the computed wave peaks. For kh > 5, cn monotonically decreases.
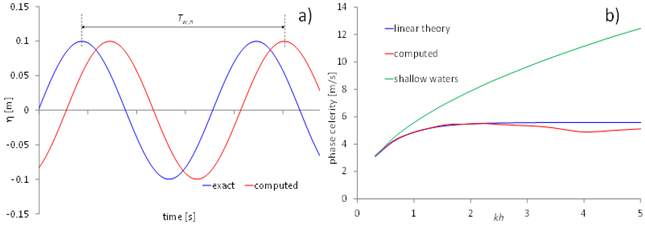
Figure 3: a) Computation of the numerical phase celerity. b) Phase speed vs. water depth.
Model Applications
Test 1: Propagation of a solitary wave in a frictionless and horizontal channel
We deal with a solitary wave, travelling in a horizontal and frictionless channel, 850 m long and 10 m wide. The initial water level h0 is 10 m, the amplitude wave aw is 2 m and the wave is initially centered at x = 200 m. The initial conditions are given by the analytical solution [11,13,37].
(61),
where
is the elevation of the free surface measured from h0, c is the wave celerity
, kw is the wave number
and the other symbols are specified as above. Left and right sides of the channel are open boundaries; the other two sides are impervious walls. The GD mesh used to discretize the channel has 160925 triangles and 84409 nodes. The mesh generator Netgen [46] has been used to create the meshes in all the applications presented in this paper. The size of the time step
is 0.025 s. The maximum value of the CFL number we computed is 1.925, where the CFL number for cell i is obtained as
(62).
In Figure 4 we show the initial condition for
, U and ws and the solutions computed after 10, 20 and 50 s. The computed absolute values of the peaks slightly decrease at the very beginning, since the initial condition is given by an analytical solution and other authors observed similar trends [8,18]. The computed peak values of
and U after 10 s are 1.926 m and 1.677 m/s, respectively. The maximum and minimum computed values of ws at the same time are 0.546 and -0.552 m/s, respectively. These values and shape of the computed profiles are almost saved at 50 s.
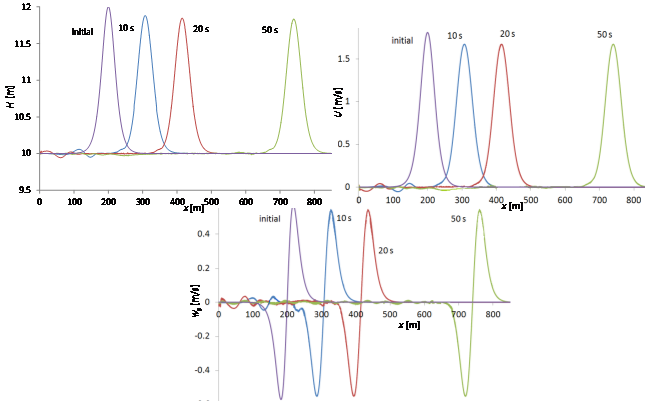
Figure 4: Test 1. H (top), U (middle) and ws (bottom). Initial solution and computed solutions after 10, 20 and 50 s.
Test 2: Moving shoreline inside a parabolic bowl. Investigation of the computational costs and convergence order
Sampson et al. [47] provided for this case the analytical solution for H, U and V (see Eqs. (39)-(40) in [48]) The domain is [8000]2 m2 with symmetric bottom with respect to the centre of the squared domain (see Eq. (38) in [48]). The GD mesh we use for spatial discretization has 272 elements and 149 nodes, and
is 40 s (we adopt the same mesh and time discretizations as in a previous paper [33], where we present a hydrostatic NLSEWs solver). The maximum CFL value obtained during the simulation is 2.82. We refine the computational mesh three times. Each refinement is performed by halving each sides of the previous coarser mesh (i.e., each triangle is divided in four equal ones). We limit the growth of the CFL number by halving the time step at each refinement. We compute the L2 norms of the relative errors of h, Uh and Vh with respect to the exact values (Table 1). The relative error for the mesh level l, errl and the rate of convergence rc, are computed as in Eqs. (70,a) and (70,b) in [33], respectively. The values of the rc are close to 2 (Table 1). The reason is that inside each triangle of the mesh, h (H), Uh and Vh change linearly, according to the three nodal values (2nd spatial approximation order). Refining the mesh, rc does not change significantly and this implies that the numerical model computes accurate results also if the domain in discretized using a coarse mesh instead of a very fine one.
Refinement
Level |
NT |
N |
L2,h |
rc,h |
L2,Uh |
rc,Uh |
L2,Vh |
rc,Vh |
0 |
272 |
159 |
3.71E-02 |
|
5.16E+00 |
|
3.31E+00 |
|
1 |
1088 |
589 |
1.10E-02 |
1.75E+00 |
1.60E+00 |
1.69E+00 |
1.00E+00 |
1.73E+00 |
2 |
4352 |
2265 |
2.90E-03 |
1.92E+00 |
4.60E-01 |
1.80E+00 |
2.70E-01 |
1.89E+00 |
3 |
17408 |
8881 |
7.46E-04 |
1.96E+00 |
1.20E-01 |
1.94E+00 |
7.00E-02 |
1.95E+00 |
Table 1: Test 2. L2 norms of relative errors and rate of convergence rc.
We use this test to investigate the computational costs (CPU times). Table 2 shows the specific mean values of the CPU times, CPUs, required for cells ordering and for the solution of the (CP+CC) steps, DC step and non-hydrostatic problem. CPUs are computed by dividing the total CPU time required for the solution of the different steps of the algorithm, by the number of the cells and the time iterations. We use a single processor Intel CORE i7-4770 at 3.40 GHz. The (CP+CC) steps are the most demanding ones, and the small decrement of the CPUs can be motivated as in section 5.8 in [33]. The DC step, the non-hydrostatic problem and the cells ordering step require CPUs approximately one magnitude order less than the one required for (CP+CC) steps.
We also measure the mean CPU times per iteration, obtained by dividing the total CPU times of the different steps of the algorithm, by the number of the time iterations. We compute the growth rate
of the mean CPU time as in Eq. (71) in [33]. Results are shown in Figure 5 and the growth exponents
are close to 1. The value of the (CP + CC) steps, slightly less than 1, can be due to the small decrement of the computational effort observed with increasing the cells number, discussed in [32]. In the same figure we also show the total CPU times, obtained by adding the mean CPU times of the four algorithm steps, and the value of its
is very close to 1.
Refinement Level |
NT |
Cells Ordering |
CP + CC |
DC |
Non-Hydrostatic |
0 |
272 |
2.81E-07 |
1.19E-05 |
7.64E-07 |
5.36E-07 |
1 |
1088 |
3.15E-07 |
1.21E-05 |
8.63E-07 |
6.15E-07 |
2 |
4352 |
3.33E-07 |
1.18E-05 |
8.44E-07 |
6.72E-07 |
3 |
17408 |
3.40E-07 |
1.17E-05 |
9.05E-07 |
6.76E-07 |
Table 2: CPUs times (seconds).
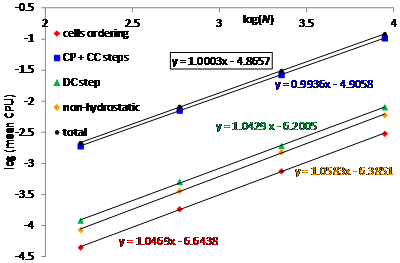
Figure 5: Mean CPU times and exponents
.
In Table D.1 (in Appendix D), we show the L2 norms of the relative errors of h, Uh and Vh, as well as the corresponding convergence orders, computed by the present solver without the non-hydrostatic solver. The norms are slightly greater than the ones obtained with the present non-hydrostatic solver, probably because of the lack of the correction of the flow field due to the components of the dynamic pressure. It is also important to compare the values in Table D.1 with the ones computed by the hydrostatic solver in [33] (Table 1 in [33].). In the solver of the referred paper, a cell-centered formulation is adopted, with a constant (1st order) spatial approximation order of the unknown variables h, Uh and Vh inside the computational cells (the triangles of the mesh). Changing from a node-centered to a cell-centered formulation, the number of the computational cells and unknowns increases. So we would expect a reduction of the errors in the solution of the cell-centered formulation. The reason of the smaller values of the errors of the present algorithm, compared to the ones in [33], could be due to the difference of the spatial approximation order of the unknown variables in the two adopted formulations.
Another benefit of the present solver with respect to the one in [33], is the abatement of the mean CPU times. In Table D.2 (in Appendix D), we list the CPUs of the solver in [33], a bit smaller than the ones in Table 1 of the present model. The reason could be the higher number of neighboring computational cells in the node-centered formulation, with respect to the three (or less, for the boundary triangles) in the cell-centered formulation. Due to the greater number of the computational cells, the total CPU times required by the cell-centered formulation (in Figure D.1, Appendix D), are greater than the ones of the present node-centered formulation (Figure 5).
Test 3: Propagation and breaking of a solitary wave over a sloping bottom
A solitary wave with ratio aw/h0 = 0.3, travels, breaks and runs up on a sloping plane beach. The measures provided in [49] constitute the reference solution for the one provided by the present model. The channel consists in a first horizontal stretch, followed by a beach with slope 1:19.85. The solitary wave in the numerical experiment is initially centered at half wavelength Lw from the beach toe [49],
(63),
For the numerical experiments, we use a 120 m long and 1.2 m wide channel, discretized with a GD mesh with 24234 triangles and 13282 nodes. The toe of the beach is 60 m far from the left channel end. We assign zero flux at the right side of the domain, and the boundary conditions at the other sides of the domain, as well as the initial conditions, are as in test 1. The size of the time step is 0.016 s and the maximum computed value of CFL is 1.17. In Figure 6 we compare the simulated and the measured free surface elevations. The length and time scales are normalized by the initial still water level h0 and (h0/g)1/2, respectively. When the wave propagates over the inclined beach, its front skews and, according to the experimental data, it breaks around t(g/h0)1/2 = 20. This is accurately reproduced by the proposed model. Several numerical models equipped with special treatment for wave breaking, not often perform very well and fail in reproducing wave breaking in time and/or amplitude [13]. After t(g/h0)1/2 = 20, the front of the wave moves towards the shoreline and the height of the wave dramatically reduces. The wave progressively runs up to the beach and reaches the maximum height around t(g/h0)1/2 = 45. The present model simulates very well the run-up process. During the draw-down, a hydraulic jump is formed approximately at t(g/h0)1/2 = 50. This is accurately simulated by the present model and, generally, good agreement is obtained till the end of the wave retreat process. During the draw-down at t(g/h0)1/2 = 55, several authors [8,13,50] compute numerical results that not perfectly match the experimental data. On the opposite, the proposed model matches very well the measures at t(g/h0)1/2 = 55. Dimakopoulos et al. [51] simulated the same test case using OpenFOAM© [3]. Their results are consistent with the experimental ones. Dimakopoulos et al. [51] discretize the domain with 180000 3D cells and their total simulation time is 10s. They use 12 CPU cores with 2.6 GHz, with a total CPU time of 2 hrs. For the simulations of the present model we use a single processor Intel Q 6600 with 2.4 GHz. The total simulation time is 25 s, requiring 425 s of computational time [49].

Figure 6: Test 3. Measured (circles) and simulated (blue solid line) surface profiles. Measures.
Test 4: Run-up of a solitary wave on a conical island
We deal with the run-up of a tsunami on a conical island [52]. The lab flume (30 m wide and 25 m long, in Figure 7) presents an island, i.e., a truncated circular cone, 0.625 m high, with diameters 7.2 m and 2.2 m at the toe and crest, respectively, and slope of the face 1:4. The surface of the physical model is made of smooth concrete and we assume zero Manning friction coefficient. Other details of the experiments can be found in [52].

Figure 7: Test 4. Definition sketch.
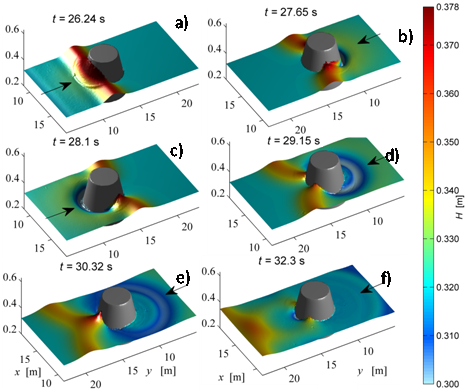
Figure 8: Test 4. Snapshot of the water surface for aw/h0 = 0.181 at different times. The black arrow indicates the direction of the incident wave.
The initial conditions are as in tests 1 and 3, and all the boundaries of the domain are open. The domain is discretized with a GD mesh with 143622 triangles and 72467 nodes. The initial water depth value h0 in our numerical run is 0.32 m and we studied three cases with relative wave heights aw/h0 = 0.045, 0.096 and 0.181, respectively. These experiments have been widely tested in the literature [8,13,17,39,45,53,54].
For brevity, we shown in Figure 8 some snapshots of the wave evolution only for aw/h0 = 0.181, where the dispersive waves are more pronounced, compared with the other two cases. In Figure 8a the wave reaches the maximum height of run-up over the front of the island. After that, the wave withdraws below the initial water level. The refracted waves partially propagate around the island towards the downstream side and two trapped waves are generated at both sides of the cone. These two waves interact at the back face of the island and generate a second run-up. Then, water waves withdraw from the back face of the island and pass through each other, moving around the cone. Figure 8e shows the first group of the dispersive waves wrapping around the island and colliding on the lee side. Figure 8f shows the second group of the dispersive waves after the collision on the back side. Similar observations have been provided in [8,54].
We compare the computed and measured water levels at gauges WG 6, 9, 16 and 22 in Figure 9. The data measured at WG 3 are used for time adjustment of the computed solutions [13]. Generally, the numerical results computed by the present solver match satisfactorily the measured time series. The run-down at the front face of the island, following the first run-up, is properly simulated. The differences between numerical and experimental data become more evident at later times, especially for aw/h0 = 0.181. Fuhrman & Madsen [53] assert that during the experiments, the front of the wave has been generated more accurately than the rear. This could motivate the above discrepancies after the initial run-up. The present model accurately describes the phase and the amplitude of the peak. The peak is slightly delayed at WG 22 for aw/h0 = 0.096 and 0.181 and at WG 9 and 16 in case aw/h0 = 0.181. The amplitude of the peak is reasonably predicted by the present model, which slightly overestimates the amplitude of the leading wave at WG 9 for aw/h0 = 0.096 and 0.181. The depression after peak at WG 9 is slightly underestimated for aw/h0 = 0.096 and overestimated for aw/h0 = 0.181. Other literature models [53,54], over predict the amplitude of the peak at WG 9, 16 and 22, expecially for aw/h0 = 0.18.
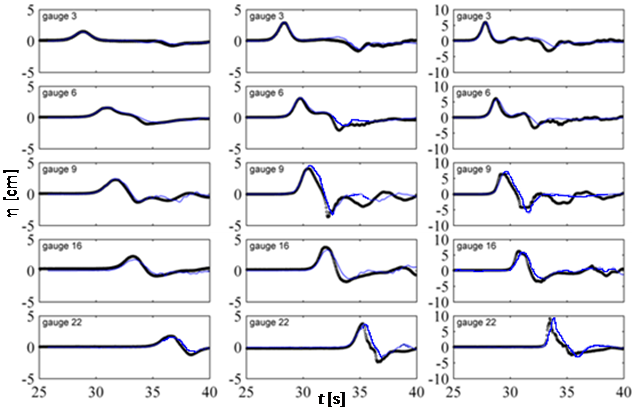
Figure 9: Test 4. Measured (circles) and simulated (blue solid line) time evolution of water level at the gauges. Measures from [8].
(Left panel),
(Middle panel),
(Right panel).
Dimakopoulos et al. [51] applied the open source code OpenFOAM© [3] to reproduce the same test. They simulated half domain, discretized with 6000000 3D cells for a total simulation time 17 sec [51]. Their results are consistent with the experimental ones and very similar to the one provided by the present model. Dimakopoulos et al. [51] used 12 CPU cores with 2.6 GHz, with a total CPU time 24 hrs. The total simulation time in our run is 20 s and, over one processor Intel Q 6600 with 2.4 GHz, the total CPU time is 1795 s.
Test 5: Tsunami in the Monai valley
This benchmark concerns a laboratory scale model of the real 1993 Hokkaido Nansei-Oki Tsunami even, around the Monai Valley. The experimental runs have been performed in the 1:400 scale lab flume of the Central Research Institute for Electric Power Industry (CRIEPI) [55]. Field observations of the real event refer to an initial leading depression wave, usually reproduced in the laboratory by an N-wave [9]. Figure 10, 10.a & 10.b show the bathymetry of the model and the incoming N-wave, respectively [56]. This is assumed as Dirichlet condition assigned at the offshore (western) boundary of the computational domain free slip condition is imposed at the two lateral sides (impervious walls). The GD mesh has 33004 triangles and 16730 nodes and
is 0.01 s. The Manning's coefficient n is 0.012 s/m1/3 [9]. The maximum value of the computed CFL number in our simulation is 4.93. Three gauges, located in front of the coast, behind the Muen Island (coordinates (4.521 m, 1.196 m), (4.521 m, 1.696 m) and (4.521 m, 2.196 m), respectively for gauges 1, 2 and 3), have been used for the time registration of the free surface elevation. In Figures 11, 11.a to 11.c shows some snapshots. A series of waves with short period are generated, during the leading depression, by the dispersion of the incoming N-wave over the coastal relief (Figure 11a). The incident wave shoals over the plane slope of the relief and refracts and diffracts around the Muen Island (Figure 11b). After reflection at the coast, some small-amplitude dispersive waves are generated (Figure 11c). At the same time, the waves reflected at the coast interact and generate some breaking waves (Figure 11c). In Figure 12 we compare the measured and the computed elevation of the free surface. The model matches very well the registrations. The initial draw-down, the arrival time and the amplitude of the leading wave are properly reproduced by the model, as well as the reflection at the coast. The discrepancy, approximately for the first 10 s, especially at gauge 1, are due to the initial condition inside the tank of the flume, where
was not uniformly equal to zero [57].

Figure 10: Test 5. a) Bathymetry of the lab model. b) The N-wave assigned at the western side [56].
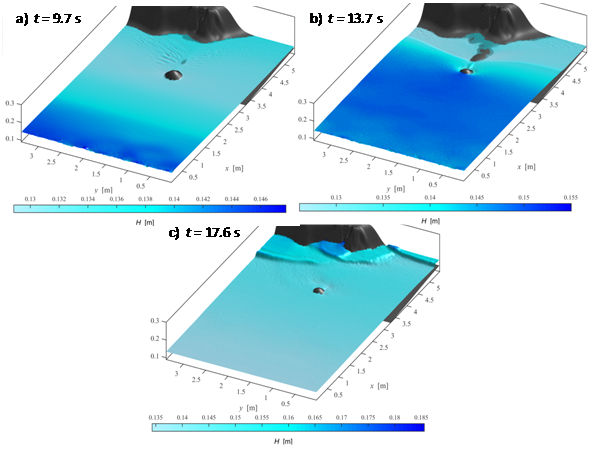
Figure 11: Test 5. Snapshots of the water levels at different simulation times.
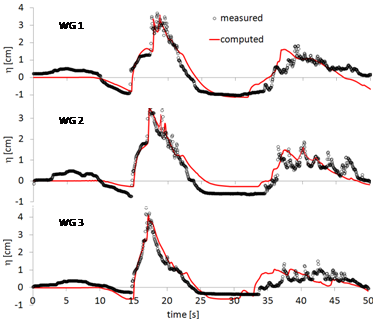
Figure 12: Test 5. Measured (circles) and simulated (red solid line) water levels at the gauges. Measures from [56].
Kesservani & Liang [58] simulated the same benchmark with different numerical solvers: a Discontinuous Galerkin (RKDG2) scheme, an adaptive-grid RKDG2 and a MUSCL2 scheme with 2nd spatial approximation order. They used different resolutions of the spatial discretizations with quadrilateral cells for the RKDG2 scheme [58]. The number of the elements ranged approximately from 7000 to 42000 for the simulation of the adaptive-grid RKDG2, and they used a uniform mesh with 95648 elements for the MUSCL2 scheme [58]. Kesservani & Liang [58] performed their simulations, reproducing a total duration of 25 s, using one processor Core Duo T9400 at 2.53 GHz. The total CPU times required by the models in [58] are listed in Table 4 of the same paper, and range from 0.25 hrs to 8.8 hrs for the RKDG2, 0.75 hrs for the MUSCL2 solver and 1.52 hrs for the adaptive-grid RKDG2. We used one processor Intel Q 6600 at 2.4 GHz and the total computational time was 0.425 hrs for a total simulation time of 200 s. The outputs of the present solver are similar to the results of the adaptive-grid RKDG2 and MUSCL2 schemes in Figure 14 [58], which required higher computational burden. The simulation with the RKDG2 with (98 x 61) elements in [58] obtained CPU times comparable to ours, but returned very bad solutions (Figures 14a-14c).
Conclusions
A non-hydrostatic NLSWEs model has been proposed for the simulations of long waves/tsunamis processes in shallow waters regions. It is our opinion that one of the principal merit of the present solver with respect to others literature schemes proposed for the solution of the same equations [13,19,39,49,] is that in both the hydrostatic and dynamic steps, the computed flow field satisfies the depth-integrated continuity equation discretized in each computational cell. As addressed in the previous sections, this has important implications in the local and global mass balance of the numerical solver. We provide several applications involving breaking/non-breaking waves and run-up, also over irregular topography. Generally, the computed results are in good agreement with the analytical solutions or lab data and with the results provided by other literature algorithms. Another important merit of the proposed model concerns the required computational effort. The CPU times are several magnitude order less than the ones of 3D models and, generally, much less that the ones of other 2D depth-integrated NLSWEs models. All the steps of the proposed algorithm can be parallelizable, as an important future advancement for this study, since it could reduce the computational burden. The parallelization of the hydrostatic CP and CC steps could be obtained by simultaneously solving the ODEs systems in all those cells next to already solved cells with higher and lower values of the approximated potential, respectively. The solution of the systems by the conjugate gradient method, in the hydrostatic DC and dynamic steps, is naturally parallelizable [59]. As a consequence of these considerations, the proposed solver could be embedded in a more general forecasting and prevention tool for the inundation generated by tsunamis or solitary waves.
Disclosure Statement
Some details of the proposed numerical procedure are provided in the file "supplementary material.docx" (Appendices A, B and C), as well as some of the figures and tables concerning the presented test cases (Appendix D).
Acknowledgment
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Conflict of Interest
The Author of the paper, Costanza Aricò, discloses any actual or potential conflict of interest including any financial, personal or other relationships with other people or organizations within three (3) years of beginning the submitted work.
References
- Goring DG (1979) Tsunamis-The propagation of long waves onto a shelf. Ph.D. Thesis, CalTech, California Institute of Technology, California, USA, pp 356.
- Chanson H (2006) Tsunami surges on dry coastal plains: application of a dam break wave equation. Coast Eng Journal 48(4): 355-370.
- (2013) OpenFOAM User Guide. The Architects of OpenFOAM, OpenFOAM Foundation.
- Dalrymple RA, Rogers BD (2006) Numerical modeling of water waves with the SPH method. Coastal Engineering 53(2-3): 141-147.
- Hirt CW, Nichols BD (1981) Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 39(1): 201-225.
- Peregrine DH (1967) Long waves on a beach. J Fluid Mech 27(4): 815-827.
- Brocchini M (2013) A reasoned overview on Boussinesq-type models: the interplay between physics, mathematics and numerics. Proc Math Phys Eng Sci 469(2160): 20130496.
- Yamazaki Y, Kowalik Z, Cheung KF (2008) Depth-integrated, non-hydrostatic model for wave breaking and run-up. Int J Num Meth Fluids 61(5): 473-497.
- Yamazaki Y, Cheung KF, Kowalik Z (2011) Depth‐integrated, non‐hydrostatic model with grid nesting for tsunami generation, propagation, and run‐up. Int J Num Meth Fluids 67(12): 2081-2107.
- Zelt JA (1991) The run-up of nonbreaking and breaking solitary waves. Coastal Eng 15(3): 205-246.
- Walters RA (2005) A semi-implicit finite element model for non-hydrostatic (dispersive) surface waves. Int J Num Meth Fluids 49(7): 721-737.
- Wei G, Kirby JT, Grilli ST, Subramanya R (1995) A fully nonlinear Boussinesq model for surface waves. Part 1: Highly nonlinear unsteady waves. J Fluid Mech 294: 71-92.
- Wei Z, Jia Y (2014) Simulation of nearshore wave processes by a depth-integrated non-hydrostatic finite element model. Coast Eng 83: 93-107.
- Kim DH, Lynett PL (2011) Dispersive and Non-hydrostatic Pressure Effects at the Front of Surge. ASCE ASCE J Hydraul Eng 137(7): 754-65.
- Soares-Frazao S, Zech Y (2002) Undular bores and secondary waves experiments and hybrid finite-volume modelling. J Hydraul Res 40(1): 33-43.
- Casulli V, Stelling GS (1998) Numerical simulation of 3D quasi-hydrostatic, free-surface flows. J Hydraul Eng 124(7): 678-686.
- Cui H, Pietrzak JD, Stelling GS (2012) Improved efficiency of a non-hydrostatic, unstructured grid, finite volume model. Ocean Modelling 54(55): 55-67.
- Stelling GS, Zijlema M (2003) An accurate and efficient finite-difference algorithm for non-hydrostatic free-surface flow with application to wave propagation. Int J Num Meth Fluids 43(1): 1-23.
- Witham GB (1974) Linear and nonlinear waves. John Wiley and Sons, UK.
- LeVeque RJ (1992) Numerical Methods for Conservation Laws. In: Birkhauser (Ed.), Lectures Notes in Mathematics (2nd edn), ETH, Zurich, Springer, Switzerland, pp. 220.
- Toro EF (2009) Riemann solvers and numerical methods for fluid dynamics: A practical introduction. (3rd edn), Springer, Dordrecht, UK, USA, pp. 724.
- Toro EF (2001) Shock-Capturing Methods for Free-Surface Shallow Flows. Wiley and Sons Ltd, UK, pp. 326.
- Toro EF, Garcia-Navarro P (2007) Godunov-type methods for free-surface shallow flows: A review J Hydr Res 45(6): 736-751.
- Fang KZ, Liu ZB, Zou ZL (2014) Modelling coastal water waves using a depth integrated, non-hydrostatic model with shock-capturing ability. J Hydraul Res 53(1): 119-113.
- Zijlema M, Stelling GS (2008) Efficient computation of surf zone waves using the nonlinear shallow water equations with non-hydrostatic pressure. Coastal Engineering 55(10): 780-790.
- Balzano A (1998) Evaluation of methods for numerical simulation of wetting and drying in shallow water flow models. Coastal Engineering 34(1-2): 83-107.
- Brocchini M, Svendsen IA, Prasad RS, Bellotti G (2002) A comparison of two different types of shoreline boundary conditions. Comput Meth Appl Mech Eng 191(39-40): 4475-4496.
- Gourgue O, Comblen R, Lambrechts J, Kärnä T, Legat V, et al. (2009) A flux limiting wetting-drying method for finite-element shallow-water models, with application to the Scheldt Estuary. Advances in Water Resources 32(12): 1726-1739.
- Aricò C, Sinagra M, Begnudelli L, Tucciarelli T (2011) MAST-2D diffusive model for flood prediction on domains with triangular Delaunay unstructured meshes. Advances in Water Resources 34(11): 1427-1449.
- Aricò C, Tucciarelli T (2007) MAST solution of advection problems in irrotational flow fields. Advances in Water Resources 30(3): 665-685.
- Aricò C, Tucciarelli T (2007) A Marching in space and time (MAST) solver of the shallow water equations. Part I: The 1D case. Advances in Water Resources 30(5): 1236-1252.
- Aricò C, Nasello C, Tucciarelli T (2007) A Marching in space and time (MAST) solver of the shallow water equations. Part II: The 2D case. Advances in Water Resources 30(5):1253-1271.
- Aricò C, Sinagra M, Tucciarelli T (2013) MAST solution of “anisotropic” flow problems: application to the shallow water equations. Advances in Water Resources 62(A): 13-36.
- Dean RG, Dalrymple RA (1991) Water Wave Mechanics for Engineers and Scientists. (2nd edn), Advanced Series on Ocean Engineering: World Scientific Publishing Co Pte Ltd, USA, pp. 353.
- Wu W (2007) Computational River Dynamics. Taylor & Francis Group, London, UK, pp. 494.
- Smit PB, Stelling GS, Roelvink D, J van Thiel de Vries, R McCall et al. (2010) X Beach: Non-hydrostatic model. Validation, verification and model description. Delft University of Technology and Deltares, Netherlands, p. 1-69.
- Wei Z, Jia Y (2013) A depth-integrated non-hydrostatic finite element model for wave propagation. Int J Num Meth Fluids 73(11): 976-1000.
- Lu X, Dong B, Mao B, Zhang X (2015) A two dimensional depth-integrated non-hydrostatic numerical model for near shore wave propagation. Ocean Modelling 96(2): 187-202.
- Zijlema M, Stelling GS, Smit P (2011) SWASH: an operational public domain code for simulating wave fields and rapidly varied flows in coastal waters. Coastal Engineering 58(10): 992-1012 .
- Putti M, Cordes C (1988) Finite element approximation of the diffusion operator on tetrahedral. SIAM J Sci Comput 19(4): 1154-1168.
- Li X, Huang W (2010) An anisotropic mesh adaptation method for the finite element solution of heterogeneous anisotropic diffusion problems. J Comp Phys 229(21): 8072-8094.
- Nag Library Manual (2005) The Numerical Algorithms Group Ltd, Oxford, UK.
- Saad Y (2000) Iterative methods for sparse linear systems. (2nd edn ) Society for Industrial and Applied Mathematics.
- Bermudez A, Vazquez ME (1994) Upwind methods for hyperbolic conservation laws with source terms, Comput. Fluids 23(8): 1049-1071.
- Lynett PJ, Wu TR, Liu PLF (2002) Modeling wave run up with depth-integrated equations. Coastal Engineering 46(2): 89-107.
- NETGEN.
- Sampson J, Easton A, Singh M (2003) Moving boundary shallow water flow in circular paraboloidal basins. Proc 6th Eng Math and Appl Conf, Sydney Australia, pp. 223-227.
- Hou J, Liang Q, Simons F, Hinkelmann R (2013) A 2D well-balanced shallow flow model for unstructured grids with novel slope source term treatment. Advances in Water Resources 52: 107-131.
- Synolakis CE (1987) The run up of solitary waves. J Fluid Mech 185: 523-545.
- Roeber V, Cheung KF, Kobayashi MH (2010) Shock-capturing Boussinesq-type model for nearshore wave processes. Coast Eng 57(4): 407-423.
- Dimakopoulos AS, Guercio A, Cuomo G (2014) Advanced numerical modeling of tsunami wave propagation, transformation and run-up. Proc. of the Institution of Civil Engineers Engineering and Computational Mechanics 167(3): 139-151.
- Briggs MJ, Synolakis CE, Harkins GS, Green DR (1995) Laboratory experiments of tsunami run up on a circular island. Pure and applied geophysics 144(3-4): 569-593.
- Fuhrman DR, Madsen PA (2008) Simulation of nonlinear wave run-up with a high order Boussinesq model. Coastal Engineering 55(2): 139-154.
- Kazolea M, Delis AI, Nikolos IK, Synolakis EC (2012) An unstructured finite volume numerical scheme for extended 2D Boussinesq-type equations. Coastal Engineering 69: 42-66.
- Matsuyama M, Tanaka H (2001) An experimental study of the highest run-up height in the 1993 Hokkaido Nansei-Oki earthquake tsunami. Proceedings of the International Tsunami Symposium, Australia, pp. 879-889.
- Tsunami Runup onto a Complex Three-dimensional Beach; Monai Valley. Noaa Center for Tsunami Research.
- Nikolos IK, Delis AI (2009) An unstructured node-centered finite volume scheme for shallow water flows with wet/dry fronts over complex topography. Comput Methods Appl Mech Engg 198(47-48): 3723-3750.
- Kesserwani G, Liang Q (2012) Dynamically adaptive grid based discontinuous Galerkin shallow water model. Advances in Water Resources 37: 23-39.
- Paglieri L, Ambrosi L, Formaggia L, Quarteroni A, Scheinine AL (1997) Parallel computation for shallow water flow: a domain decomposition approach. Parallel Computing 23(9): 1261-1277.

©2017 Arico. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.







