In the first part of this document, the degradation of the mechanical properties of the mass concrete of the Dez concrete arch dam under the long-term effects of its environment as well as its loading history has been investigated using an innovate inverse analysis method. For performing that inverse analysis, an objective function was defined and then it was attempted to minimize that. That function was defined as the sum of the squared differences between the displacements obtained from a developed enhanced FE model in the ABAQUS standard software by the authors in the current study for each assumed set of the degraded mechanical properties of the dam as input variables and those obtained from the inverse pendulum’s records of the dam. For the sake of the generality of the problem, in performing such FE analyses, it was assumed that the behavior of the concrete material of the Dez dam has transformed gradually from initial homogeneous and isotropic undamaged behavior to the heterogeneous and orthotropic deteriorated behavior under the long-term effects of the environment as well as load agencies. Hence, the vertical sections of the dam were divided into nine and six subsections along the thickness and height directions of the dam respectively. In each subsection, a transversely isotropic degraded elastic constitutive law was considered for characterizing the concrete long-term deterioration phenomenon. Obtained results revealed that the long-term deterioration of the mass concrete of the Dez dam is in fact a heterogeneous and anisotropic process because that the magnitude of the above mentioned defined objective function was obtained smaller than the corresponding value in the previous study of the authors which was performed based on the homogeneous and isotropic damage evolution assumptions. Core test results from the mass concrete of the dam reported by a consulting engineer company confirmed the concrete degradation predicted by the proposed model. After that, the behavior of this dam against an earthquake excitation was investigated considering the above mentioned degradation of its mechanical properties and the obtained results were compared with its corresponding behavior considering its initial un-damaged mechanical properties for the mass concrete. Comparisons revealed considerable growth in the enveloped tensile stresses which can change the initial assumed safety margin design factors of the dam and necessitates the re-evaluating of the dam stability.

Keywords: concrete, thermal inverse analysis, heterogeneous, transversely isotropic, long-term damage, arch dam, seismic response, finite element method

In the present study, as a promotion to the previous attempt of the authors and his co-workers, Labibzadeh et al.,¹ the degradation of mass concrete of the Dez dam was evaluated in more detail using a more sophisticated numerical degradation model. In that preceding work, it was demonstrated that the concrete of the Dez dam has been deteriorated and its mechanical properties have been changed after a long time (approximately 45years) from which the dam is under service. Furthermore, in that attempt, the degraded mechanical properties of the dam were identified using a novel thermo-elastic inverse numerical model developed in that previous research.¹ It should be noted that in that research, it was postulated that this degradation has a homogeneous and isotropic nature. Although the obtained results of some core tests conducted recently on this old dam by a consulting engineering group verified the predicted results obtained from the mentioned above numerical model and confirmed that degradation in general undoubtedly, they could not guarantee the homogeneity and isotropy of this deterioration with the same degree of certainty. Hence, in the first part of this research, the degradation of dam's concrete was considered as a heterogeneous and anisotropic process and it was decided to investigate the validity of this hypothesis using that numerical model which was developed in previous study.¹ For the sake of brevity, the description of that analytical model (thermo-elastic inverse model) has not discussed again here. But, it should be noted that, in that model, an error or residual function has been defined which plays the principal role in that mentioned above validity process. In other words, it is postulated in this study that if the computed value of the error function from the new proposed sophisticated model which will be described in the next section is obtained smaller than the corresponding value in the previous work, it can be concluded that the new numerical model has a more realistic feature and is more reliable. This assumption, in fact, is a foundation that this new research is going to be built on that. So, the degree of the reliability of the obtained results depends on the degree of the soundness of that assumption. The above mentioned error function in this study similar to the previous work, in fact, indicates the difference between the computed displacement vector of the nodal points of the dam obtained from the new presented enhanced thermo-elastic inverse model and those obtained from the inverse pendulums of the dam. Hence, the smaller the error values the more degree of the reliability of the implemented analytical model. It should be noted that the difference between the new model and the old model used in preceding study is that in the present model, the material constitutive behavior of concrete of the Dez dam is considered to be transversely isotropic in contrast to the old version which was considered as isotropic and also the degradation of the dam is defined to be heterogeneous in opposite to the forgone work which was postulated as a homogeneous phenomenon. At the end of the part one of the paper, the obtained results will confirm that the degradation of the concrete mechanical properties of the Dez dam has a heterogeneous and anisotropic feature. Second part of this study deals with the seismic assessment of this dam considering obtained degraded elastic strength against to the Tabas ground motion.

Part I: transversely isotropic elastic degraded dam

As it was mentioned in the previous research, the behavior of the dam and its abutments are still elastic based on the observations from the instruments located in the dam and supports besides to the available geological and geotechnical report of the dam at construction time.¹ From the heterogeneity point of view, it must be said that the environmental conditions at the upstream and downstream faces of the Dez dam are completely different. The upstream face of the dam is in permanent contact with the reservoir water which is completely saturated whereas the downstream of the dam is exposed to the ambient weather which is nearly dry. The wetness in Dez dam accelerates the degradation whereas dryness slows it down. The temperatures in these regions are also different. Temperature values at upstream are moderate and at downstream are excessive. Excessive temperatures accentuate the deterioration and moderate temperatures play it down for concrete. So the moisture content and temperature change significantly through the thickness of the dam at each altitude level. In addition, the variation of these two environmental parameters with respect to time is not the same for the upstream and downstream faces. Therefore, it is rational to expect that the concrete deterioration of the Dez dam cannot be a homogeneous process along the dam thickness. Furthermore, the moisture and temperature are also changing along the height direction of the dam. Hydrostatic pressure varies linearly from the top to the bottom of the dam with high magnitudes at the bottom. So, the moisture can penetrate and affect lower parts of the dam more effectively than the upper portions. On the other hand, because of the different sunshine expositions, the temperature would change along the height of the dam both in upstream and downstream faces. Hence, the concrete deterioration cannot be a homogeneous process along the dam height look likes the discussed thickness direction.

On the orientation of the anisotropy, it should be noted here that the biaxial stress resultant at the in-planes of the Dez dam (parallel planes to the dam upstream/downstream surfaces) remains approximately constant due to the main actions imposed on the dam: hydrostatic pressures and gravity loads. The existence of higher compressive stresses in arches than those verified in cantilevers at the dam upper portions and at the same time the actions of higher compressive stresses in cantilevers than those developed in arches at lower altitudes of the dam may interpret well the above mentioned hypothesis. Apart from these natural boundary conditions, the essential boundary conditions of the Dez dam also strengthen the idea of the transversely isotropic nature of the elastic degradation tensor of the Dez concrete dam. The elongations of the dam in arch and cantilever directions are nearly the same but are much greater than the dam elongation in the thickness direction. So, it is rational to expect that the degradation mechanism has different effects on the in-planes and out-of-planes (planes regarded as being perpendicular to in-planes) of the dam (Figure 1).

Figure 1 Transversely isotropic elastic degraded nature of Dez concrete.

It should be emphasized here that, the authors of this paper like Fedele et al.,² believes that the degradation of concrete due to the environmental effects only could be merely considered as an isotropic damage process in average behavior of the dam. However, due to past extreme loadings from Fedele² and his collaborators' point of view and from the opinion of the authors of this article due to permanent main ordinary loadings as well as past extreme loadings, this damage process can be transformed into an anisotropic process. Past extreme loadings such as earthquakes or unusual reservoir water reductions can produce diffused cracks within the concrete and on the other hand, the permanent main actions e.g. hydrostatic and gravity loads can provide a dominant state of stresses in the concrete, each of them makes the evolution of the long-term deterioration of the dam to take anisotropic features.

After extensive examination of the literatures, the authors^3,4 concluded that probably the only two diagnostic studies conducted on concrete dams considered the degradation of concrete as an anisotropic process. Oliveira & his collaborators³ performed a modal analysis on the Cabril arch dam located in Portugal using an inverse analysis method for dam material parameter identification. However, they have only modeled a small damaged zone (cracked zone) of the dam with an orthotropic transversely isotropic elastic constitutive law and considered the rest of the dam as isotropic material. Moreover, they have assumed that two of the fifth independent elastic modulus e.g. the elastic modulus and Poisson's ratio of the plane of isotropy are known values and only three remained unknown material parameters were identified in their research. On the other hand, Garbowski et al.,⁴ performed an inverse analysis on a roller compacted concrete dam using the so called DIC technique (Digital Image Correlation) for analyzing the obtained images from a portion of the surface of the dam which experienced some displacements under the pressure imposed on it with a flat-jack through a T-shaped slots. They have identified the elastic and shear modulus of the concrete in the presence of orthotropy. They reported that the advantage of their method was that no data from extensometers were needed. Although Garbowski⁴ and his colleagues have performed a worthwhile attempt for diagnosing the material parameters of the dam, but the authors of this paper believe that their approach may suffer from two main drawbacks. Firstly, the accuracy of obtaining results is strongly dependent on the accuracy of the field operations and related mathematical theories. Secondly, the results are obtained from a local portion and under an artificial procedure (virtual loadings and virtual resulted displacements), so they cannot be extended easily to the global mass concrete of the dam. Apart from these two mentioned deficiencies, they have considered the dam as a homogeneous medium and taken the Poisson's ratio components of transversely isotropic elastic tensors as known parameters.⁵ So, they have only identified three remained other parameters like the work of Oliveira et al.⁴

This issue motivated the authors of this article to investigate in more detail the long-term aggression of concrete of the Dez dam in the presence of anisotropy using the innovative thermal inverse analysis.¹ Considering Figure 1, the constitutive law for the long-term deterioration of Dez concrete can be stated as a relation (1):

$\left[\begin{array}{c}{\epsilon }_x\\ {\epsilon }_y\\ {\epsilon }_z\\ {\gamma }_{xy}\\ {\gamma }_{yz}\\ {\gamma }_{zx}\end{array}\right]=\left[\begin{array}{cccccc}\frac{1}{E_H}& -\frac{{\nu }_{HV}}{E_H}& -\frac{{\nu }_{HV}}{E_H}& 0& 0& 0\\ -\frac{{\nu }_{HV}}{E_H}& \frac{1}{E_V}& -\frac{{\nu }_V}{E_V}& 0& 0& 0\\ -\frac{{\nu }_{HV}}{E_H}& -\frac{{\nu }_V}{E_V}& \frac{1}{E_V}& 0& 0& 0\\ 0& 0& 0& \frac{1}{G_H}& 0& 0\\ 0& 0& 0& 0& \frac{2\left(1+{\nu }_V\right)}{E_V}& 0\\ 0& 0& 0& 0& 0& \frac{1}{G_H}\end{array}\right]\left[\begin{array}{c}{\sigma }_x\\ {\sigma }_y\\ {\sigma }_z\\ {\tau }_{xy}\\ {\tau }_{yz}\\ {\tau }_{zx}\end{array}\right]or\left\{\epsilon \right\}=\left[C\right]\left\{\sigma \right\}$ (1)

In the above relation, $E_H$  denotes the Young's modulus along the x-axis (axis of elastic symmetry) and $E_V$ indicates the corresponding elastic parameter in the plane of isotropy e.g. Y-Z plane herein. ${\nu }_{HV}$ is Poisson's ratio, characterizing the transverse strain reduction in plane of isotropy (Y-Z) due to tensile stress in a direction normal to it (X). ${\nu }_V$ represents also Poissin's ratio but in the plane of isotropy. $G_H$ stands for the shear modulus for planes normal to plane of isotropy.

According to equation (1), in this study, five independent constants of the compliance matrix; C; were considered in a general form to be the unknowns and extensive trials have been made to identify them through a thermal inverse analysis algorithm described in detail in Labibzadeh.¹

The dam was sub-divided into nine individually homogeneous zones in the thickness direction and into six similar sections along the height of the dam. To each of these sub-regions, the above mentioned five unknowns consist of two Young's modulus, two Poisson's ratios and one shear modulus were attributed as representative of the long-term concrete damage to be estimated. This subdivision was performed taking into account the Dez dam geometrical characterizations and construction practice stages as well as optimization of the time consumes for each analysis to be completed. Figures 2 & 3 shows a part of the dam with the scheme used for sub-dividing. The Word 'Block' in this figure marks the vertical cantilevers of the dam separated with the contraction joints. These contraction joints were contributed in the F.E. thermal inverse analyses.

Figure 2 Dez dam sub-divisions.

Figure 3 Dez dam sub-divisions from downstream view.

The unknowns mentioned before were determined through performing F.E. thermal inverse analyses and subsequent to each of these analyses performing parameter identification. To this end, for each assumed set of five unknown parameters, a Finite Element (F.E.) analysis has been performed taking into account the thermal loads induced in the dam due to ambient temperature gradients as well as hydrostatic and gravity loads. The details of F.E. model were completely described in the previous accompanied paper.¹ A schematic F.E. model of the dam has been depicted in Figure 4 and the true F.E. model has been shown in Figure 5.

Figure 4 Dez dam schematic F.E. model.

Figure 5 F.E. Model of the Dez dam and its support.

For dam and its geologic support modeling; 27241 and 4327 elements; correspondingly 2503 and 3471 nodal points were used respectively, leading to considering of 17992 degrees of freedom for the problem in hand. The temperature gradient for each nodal point in F.E. model was obtained using the records of the thermometers located within the dam body. Based on these data records, the gradient was defined as the difference between the recorded temperatures of a node in two different days of a specific year; in this study 2007s; (Figure 6). These days were selected in such a way that provides a relatively noticeable temperature difference in the nodes with no significant difference in the reservoir water level of the dam.

Figure 6 Recorded water level, upstream and downstream temperatures-2007s

By performing each F.E. analysis, relative displacements of the nodal points of the dam were computed and recorded in a vector named as $u_c$ (computed displacement vector). This vector is a function of those mentioned unknown parameters $\left\{p\right\}$ ; $u_c(p)$ ; based on the theory of elasticity rewritten in F.E. framework briefly here (Eqs. 2 to 4) where $\left\{p\right\}$  in turn includes two Young's modulus, two Poisson's ratios and one shear modulus, according to Eq. (1).

$K_s{u}_c=F_s$ (2)

$K_s={\displaystyle \underset{\Omega }{\int }{B}^{T}DBdV}$ (3)

$D=f\left(E_H;E_V;{\nu }_V;{\nu }_{HV};G_H\right)$ (4)

$K_t={\displaystyle \sum _{i=1}^n{K}_s;}{F}_t={\displaystyle \sum _{i=1}^n{F}_s}$ (5)

In relations 2 to 4, $K_s$ is the stiffness matrix; $F_s$ denotes the corresponding nodal force vector contains the effects of gravity, hydrostatic and thermal actions; B is the strain-displacement matrix; D indicates the transversely isotropic elastic fourth tensor $\left(\left[D\right]={\left[C\right]}^{-1}\right)$ and $\Omega$ is the volume of each sub-divisions of the dam. Eq. (5) states that the total stiffness and force vector are obtained through assembling procedure in F.E. method. After that, the vector $u_c$ was subtracted from a vector collecting their experimental data counterparts $u_s$ (recorded displacements in each node with pendulums) to obtain a residual vector $R(p)$ :

$R(p)=u_s-u_c(p)$ (6)

It should be noted here that the recorded displacements are limited to specific regions of the dam where the inverse pendulums are located. For the other regions, rational interpolation and extrapolation schemes have been followed to obtain the required unavailable data. Then, a traditional discrepancy function J was formulated as a quadratic form of obtained residuals as follows:

$\mathrm{J}\left(p\right)=R{\left(p\right)}^{T}IR\left(p\right)$ (7)

Where I denotes the identity matrix. The solution is defined as a set of the variables $\left\{p\right\}$ which minimizes the function J.

Long-term deterioration: heterogeneously and orthotropically

After performing sensitivity analyses on the material parameters, it was revealed that the function J did not alter through the variation of the thermal expansion coefficient so this parameter was considered as a constant and equal to the value which obtained before from the previous study of the authors; thermal expansion coefficient $=\alpha =6*{10}^{-6}1/˚C$ .¹ However, it was also pointed out that the magnitude of error function J changes noticeably when the Poisson's ratios change. This is in contrast to the results of Oliveira et al.³ and Garbowski et al.⁴ In the following, the obtained results of this study have been outlined in Table 1-3. For the sake of brevity, all the results are not presented here.

In the above tables, the word 'zone' points to the subdivisions numbered in Figure 2; J₁, J₂ and J₃ are defined based on the Eq. 7 as below:

$\begin{array}{l}{J}_1={\left(u_c{}_{285}(p)-{\overline{u}}_{s285}\right)}^{T}I(u_c{}_{285}(p)-{\overline{u}}_{s285})\\ J_2={\left(u_c{}_{315}(p)-{\overline{u}}_{s315}\right)}^{T}I(u_c{}_{315}(p)-{\overline{u}}_{s315})\\ J_3={\left(u_c{}_{331}(p)-{\overline{u}}_{s331}\right)}^{T}I(u_c{}_{331}(p)-{\overline{u}}_{s331})\end{array}$ (8)

$u_c{}_{285}$ denotes for example the computed relative displacement at the elevation 285 of the dam and ${\overline{u}}_{s285}$ refers to the recorded corresponding value with pendulums. The relation between the function J and J₁, J₂, J₃ is defined as below:

$J=J_1+J_2+J_3$ (9)

In Table 1, E_H and E_V stand for the out-of-plane and in-plane elastic modulus respectively. As it is seen in that table, for each of this modulus, three different columns have been assigned. Each column indicates a zone of the dam (Figure 2); zone 1 denotes upstream, zone 5 marks central and finally zone 9 refers to downstream parts of the dam. $u_c{}_{331},u_c{}_{315}and{u}_c{}_{285}$ indicate the relative displacement component in upstream-downstream direction of the dam, which have been computed by the proposed FE numerical model at the elevations 331, 315 and 285 of the dam in which there exist corresponding recorded values by the inverse pendulums of the dam i.e. ${\overline{u}}_{s331},{\overline{u}}_{s315}and{\overline{u}}_{s285}$ . As it has been explained in the previous study, the relative displacements are in fact the difference between displacements of a particular point of the dam in two different days of the year 2007 which these days as are specified in Figure 6 are selected in such a way that the level of the reservoir is the same for these days but there is the maximum difference between the temperatures recorded by thermometers for them.¹ J₁, J₂, J₃ and error function J in Table 1 are those parameters that defined in eqs. (8) and (9). The same parameters have been used in Tables 2 & 3. In table 2, ${\nu }_{H}and{\nu }_{HV}$ refer to the Poisson’s ratios at out-of-plane and in-plane respectively (Figure 1). The last independent material parameter as defined by eq. (1) is the G_H which denotes the out-of-plane shear modulus of the dam and used in Table 3. It is worth mentioning that the above tables have been shown in this paper in an order agrees with the order that inverse parameter identifications were performed in this attempt. Hence, the optimum or minimum of error function J can be found in the last table (Table 3). This value (5.085E-07) is ten times smaller than the corresponding value obtained before by the authors,¹ e.g. 1.37 E-06 based on the assumption of homogeneity and isotropy. Therefore, the question was asked in the beginning of this article now can be replied; the long-term deterioration process of concrete of the Dez dam is both heterogeneous and anisotropic. Figures 7-9 show the variations of the identified material parameters in a typical vertical section of the Dez dam.⁶

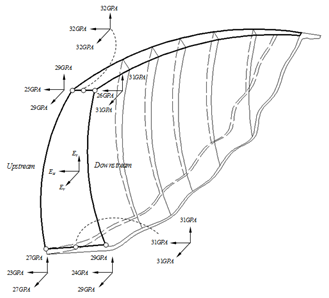
Figure 7 Variation of the out-of-plane E_H and in-plane E_v elastic modulus (GPA) in a typical vertical section of the Dez dam.

Figure 8 Variation of the out-of-plane ${\nu }_{HV}$  and in-plane ${\nu }_V$ Poisson's ratios in a typical vertical section of the Dez dam.

Figure 9 Variation of the out-of-plane $G_H$  and in-plane $G_V$ shear modulus (GPA) in a typical vertical section of the Dez dam.

Figures 7-9 represented the spatial variation of the elastic stiffness moduli obtained for the year 2007s. Another interesting issue for the designer engineers can be that how do these elastic moduli change over time. This question is responded in Figures 10 & 11. In these figures, the performances of deterioration of out and in plane elastic stiffness modulus with respect to time are depicted. These figures, demonstrate that the rate of deterioration in the elastic stiffness of the dam in the upstream-downstream direction is more than the corresponding rate in the vertical direction. Also, these pictures indicate that this rate has been accelerated in the second twenty years of the time interval considered for analysis.

Figure 10 Time variation of out-of-plane elastic stiffness modulus.

Figure 11 Time variation of in-plane elastic stiffness modulus.

Based on the obtained results, the central part of the dam has not altered yet by any degradation due to aging. By moving from this central part to the downstream and upstream faces of the dam, it was observed that the elastic modulus decreased significantly. This reduction is more noticeable for the out-of-plane elastic modulus e.g. elastic modulus along the upstream-downstream direction in comparison to the in-plane elastic modulus (plane of isotropy) of the dam. With respect to the Poisson's ratio on the other hand, it was revealed that the long-term damage of this parameter is not a heterogeneous and anisotropic process like to what observed for the elastic modulus and is a homogeneous and orthotropic damage. The out-of-plane Poisson's ratio was obtained greater than in-plane correspondent value. A similar observation of Poisson’s ratio was obtained for the shear modulus. The out-of-plane shear modulus was obtained smaller than the in-plane corresponding value. These results confirm that the small thickness of the Dez dam and the actions of the main loads establish a state of stress which makes the long-term degradation of the Dez dam to be anisotropic. At the same time, the change in hydrostatic pressure and gravity loads along the height of the dam as well as the existence of a difference between the environmental conditions at upstream and downstream faces of the dam are responsible for heterogeneity in that mentioned damage evolution.

Part II: seismic response of the strength degraded dam

As it was demonstrated in the first part of this study, the elastic strength of the Dez dam has been reduced during its service life. In this part, in order to evaluate the seismic behavior of the dam in its current condition, dam was simulated against to an earthquake excitation. Figure 12 shows the accelorogram of the Tabas ground motion which was selected in this study as the support shaker.

Figure 12 Tabas earthquake excitation.

The element types used for FE simulation⁷ of the dam-reservoir-foundation system have been outlined in Table 4. The length of the reservoir was considered as three times of the height of the dam in the above mentioned FE simulation. Hence, the seismic waves travels to the far end of the reservior are completely damped. This FE model has been illustrated in Figure 13. For considering the dynamic effects on the elastic behavior of the dam during the earthquake analysis, the degraded Young and shear moduli obtained from the part I of the paper, highlighted in Tables 1 & 3, were increased 15%.

Figure 13 Dam-reservoir-foundation model of the Dez dam.

For assistance of the readers in better investigating of the change in the seismic resistance of the Dez dam, the envelope of the non-concurrent maximum principal stresses on the upstream and downstream faces of the dam were compared in Figure 14 & 15 with the corresponding result obtained by Hariri & Mirzabozorg.⁸ These researchers did not consider any degradation for the mass concrete of the dam during its service life. As it can be seen from this picture, current study shows significant reduction in the compressive stress regions (blue colored areas) of the dam due to ageing effects. These results were obtained for the reservoir water levels equal to 188 and 56 m. These levels were marked in Figure 16 across the height of the dam. As it can be seen from this figure, those levels of water correspond to the maximum and minimum water levels produce the largest and smallest hydro-dynamic pressures on the upstream face of the dam respectively.

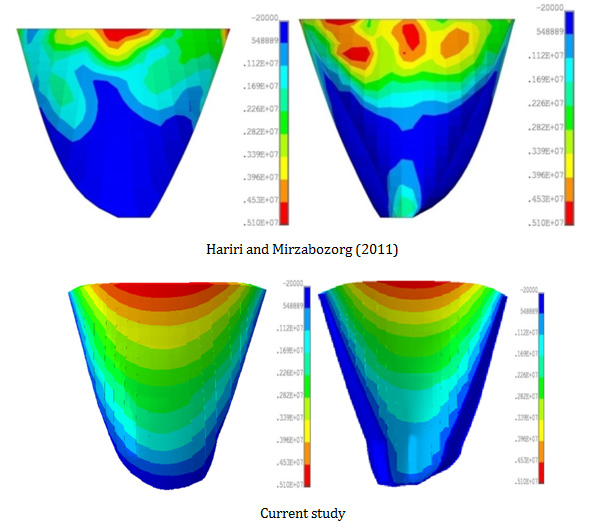
Figure 14 Non-concurrent envelope of the maximum prinicipal stresses of the Dez dam-level of reservoir water is 188 m.

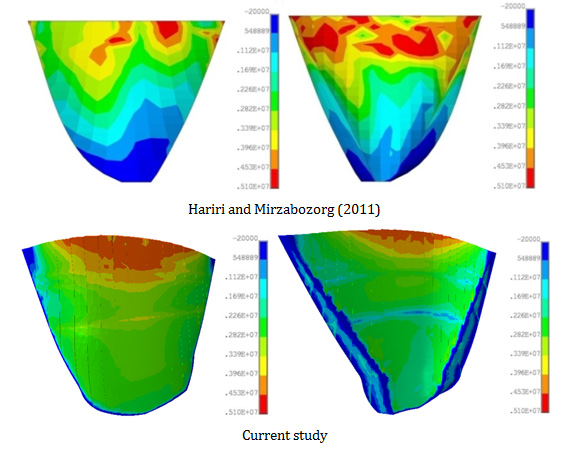
Figure 15 Non-concurrent envelope of the maximum principal stresses of the Dez dam-level of reservoir water is 56 m.

Figure 16 Reservoir water levels considered in seismic analyses.

Figure 17 compares three time history records of displacement obtained for the crest of the Dez dam. The blue colored curve indicates the result obtained by Hariri & Mirzabozorg⁸ and the red and green colored lines correspond to the current study results obtained with two assumptions, without degradation and with degradation. According to this diagram, it can be deduced that the largest displacement amplitude has been obtained for the dam considering the strength degradation determined in the part I of this article (red colored curve in Figure 17).

Figure 17 Displacement time histories of the Dez dam crest.

In this paper, subsequent to the previous attempt done by the authors on the Dezdam¹ and based on that, an effective thermo-elastic inverse analysis⁹ has been implemented for in-detail elastic properties identification of this dam after a long time being passed from its operation life. In this new work, the property of age-related degradation of the dam was investigated from the heterogeneity as well as anisotropy point of views. By reviewing the obtained results it was revealed that the ongoing deterioration of the concrete material of the Dez dam is a heterogeneous and orthotropic process. Heterogeneity is due to the difference in the environmental conditions circumvented the dam as well as the change of hydrostatic and gravity loads along the height of the dam and anisotropy because of the shape of the dam and state of stresses resulted from the permanent external loading exposed on the dam. Furthermore, the effects of this degradation were investigated in the seismic response of the dam. Obtained results in this stage demonstrated that the deterioration of the mass concrete of the dam leads to the enlargement of the tensile stresses in the dam which indicates the reduction in the seismic resistance and safety margin design factors of the Dez dam.^10‒16

Authors are so grateful to Yaqub Arab, the head and his assistants Ebrahim Barati Choobi and Kambiz Amiri in Dam Stability Control Center of Water & Power Authority of Khouzestan Province of Iran.

Author declares that there is no conflicts of interest.