Liquid phase epitaxy apparatus and features of Hg1-xCdxTe layers

doi:10.15406/eetoaj.2018.02.00036

eISSN: 2641-936X

Electrical & Electronic Technology Open Access Journal

Research Article Volume 2 Issue 5

Liquid phase epitaxy apparatus and features of Hg_1-xCd_xTe layers

Sh O Eminov

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Institute of Physics of NAS Azerbaijan, Azerbaijan

Correspondence: Sh O Eminov, Institute of Physics of NAS Azerbaijan, Azerbaijan

Received: July 21, 2017 | Published: November 28, 2018

Citation: Eminov SO. Liquid phase epitaxy apparatus and features of Hg_1-x Cd_x Te layers. Electric Electron Tech Open Acc J. 2018;2(5):322-325. DOI: 10.15406/eetoaj.2018.02.00036

Download PDF

Abstract

The empirical expressions for liquids isotherms of Te –rich angle of Hg-Cd-Te phase diagram were used for evaluation of influence of the preliminary synthesis of the ${(H g_{1 - z} C d_{z})}_{1 - y} T e_{y}$ melt-source on the reproducibility of both the liquidus temperature of the melt and ${(H g_{1 - z} C d_{z})}_{1 - y} T e_{y}$ epitaxial layer composition. A new expression for the liquidus line has been formulated. ${(H g_{1 - z} C d_{z})}_{1 - y} T e_{y}$ layers with x~0.2-0.22 have been grown in a novel Liquid phase epitaxy apparatus that preserves the surface from residual melt drops. The effects of thermal annealing on electrical properties and crystallinity of epitaxial layers are considered.

Keywords: liquid phase epitaxy, lpe, hgcdte, liquidus isotherms, lpe growth apparatus

Introduction

The II-VI compounds of wide gap semiconductor CdTe (E_g =1.6eV) and semimetallic compound HgTe (having negative energy gap E_g-0.3 eV) form a continuous series of pseudobinary solid solutions of Hg_1-xCd_xTe with cubic zincblende structure. The gap in these alloys varies nearly linearly with x between the two end –point values $0 \leq x \leq 1$ . For that reason the alloys can be tailored to cover a broad range of energy gaps: with high bandgaps (of interest for solar cells operating at wavelength in the vicinity of 1µm) and low bandgaps (of interest for detectors and lasers operating in vicinity of 10µm and beyond). The basic properties of Hg_1-xCd_xTe such as high electron mobility, relatively low dielectric constant, long minoriry carrier lifetimes and high electrooptic coefficients are very suitable for the development of complex devices. Hg_1-xCd_xTe is a preferred material to fabricate new generation infrared focal plane arrays because of its high quantum efficiency, tunable absorption wavelength, and wide operating temperature range.^1-5 The lattice mismatch between Hg_1-xCd_xTe and CdTe is only 0.3% and Hg_1-xCd_xTe layers can be precisely lattice matched to Cd_0.04 Zn_0.96Te. For this reason high quality 5-20µm thick active epitaxial layers of HgCdTe on lattice matched Cd_0.04 Zn_0.96Te.⁶ substrates are most widely utilized for fabricating IR detectors.

An important industrial growth technique for obtaining device-quality Hg_1-xCd_xTe material is the liquid phase epitaxy (LPE) method. Briefly, the LPE is a part of the production process of semiconductors: inside a heated furnace a substrate CdZnTe is dipped into the melting pot which is filled with compound of the molten materials cadmium, mercury, and tellurium. By reducing the temperature of the heaters inside the furnace a thin single crystalline film begins to grow onto the surface of the substrate to form the epitaxial layer. The temperature data outside the pot is available from measurements and as simulation data and acts as boundary condition for the inside temperature. The main approaches for LPE growth of Hg_1-x Cd_xTe, layers are equilibrium cooled and step-cooled techniques where the substrate is put in contact with a supersaturated or saturated solution. In equilibrium cooling the saturated melt-solution is in contact with the substrate at the liquids temperature ( $Θ_{L}$ ) and the temperature is lowered slowly, the solution becomes supersaturated; meanwhile a slow epitaxial growth on the substrate is initiated. The second is the step-cooling process, in which the saturated solution is cooled down a few degrees (5–20K) to obtain a supersaturated solution. The substrate is then brought in contact with the solution, which is kept at this cooled temperature. Growth occurs first due to the supersaturation, and will slow down and stop finally. For both techniques, if the substrate is dipped in sequence into several different melt sources, multiple layer structures can be grown. LPE can successfully and inexpensively grow homo- and heterostructures. As the growth is carried out under thermal equilibrium, an epilayer with a very low native defect density can be obtained. The substrate is withdrawn from the melt after desired thickness of epitaxial layer grown.

Evaluation of Hg-Cd-Te phase diagram

Epitaxial growth of epitaxial layers of HgCdTe from liquid solutions can be accomplished from Hg-rich , Te-rich and pseudobinary HgTe-CdTe solitions. The selection and knowledge of a correct phase diagram is prerequisite issue for estimation of melt composition. There are two versions of solid-liquid phase diagrams representing Hg-Cd-Te ternary system available in the literature. These are Harman's experimental³ and Brebick's theoretical one based on his associated solution model.⁴ The liquidus lines in both the diagrams match well while there is a significant difference in the solidus curves. Acritical comparison of the two revealed that the Harman's diagram was established under nonequilibrium and high Hg overpressure condition which has resulted in solidus estimation biased towards HgTe rich compositions. With the determined ${(H g_{1 - z} C d_{z})}_{1 - y} T e_{y}$ solution composition (y,z), it is possible to calculate both the liquidus temperature $Θ_{L} ({}^{\circ}C)$ and Xusing the Te-rich angle of phase diagram data given by Harman³shown in Figure 1.

Figure 1 Te-rich angle of Hg-Cd-Te phase diagram given by Harman.³

In the following expressions for these parameters can be found :

$Θ ({}^{\circ}C) = 1102 + 250 z + 420 z y - 785 y$ (1)

$x = z / (0.22 + 0.78 z)$ (2)

Here, $z = C_{H g}^{l} {(C_{C d}^{l} + C_{H g}^{l})}^{- 1}$ , $C_{H g}^{l} = (1 - z) (1 - y)$ , and $y = C_{T e}^{l}$ .

Rewriting relations (1) yields

$Θ = 1352 - 365 C_{T e}^{l} + 420 C_{H g}^{l} - 670 C_{H g}^{l} / (1 - C_{T e}^{l})$ (3)

$x = (1 - C_{H g}^{l} - C_{H g}^{l}) / (1 - 0.78 C_{H g}^{l} - C_{T e}^{l})$ (4)

The difference between experimental results and those calculated from expression (1) using values of available in the literature reaches the markedly high figure of 5–8ºC. The reason for this is mainly related to the difference between the actual LPE growth conditions used in an each referred work and the conditions under which the data for the phase diagram was obtained. With the purpose of reducing this difference, we considered Harman’s phase diagram data and revealed that with $y < 0.65$ they contain dots that, in practice, are not used for LPE growth and significantly complicate the $Θ = Θ (y, z)$ dependence. We have excluded these dots with $y < 0.65$ from consideration and obtained a new relation for solutions with $y \geq 0.65$ by use numerical methods:

$Θ = 1144 - 845.4 y + 672.6 z$ (5)

Rewriting the above relation yields

$Θ = 1144 - 845.4 C_{T e}^{l} + 672.6 C_{H g}^{l} {(1 - C_{T e}^{l})}^{- 1}$ (6)

Calculated and experimental $Θ (C^{\circ})$ values are plotted in Figure 2. The calculated values are found to be in good agreement with the experimental data. We applied relations (3) and (4) to evaluate the impact of Hg pressure at the stage of solution preparation at 700–710ºC inside of sealed ampoule on the run-to-run reproducibility of both $Θ$ and xvalues. The following approach was used to evaluate these magnitudes. The mass $Δ m_{H g}$ of the excess Hg that would be added into a closed system with free space $V (c m^{3})$ to compensate the evaporation from the solution at temperature T(K) can be evaluated by applying the Clapeyron equation, $Δ m_{H g} = 12.2 (P_{H g} V / T) 200.61$ (mg), where $P_{H g}$ is the equilibrium partial pressure (in atm) of Hg over the solution. The $\log P_{H g} (x, T)$ curves for the specified x value points in a three-phase equilibrium Hg-Cd-Te system are available in⁵ At T~700–720ºC the curves are so sharp that a precise estimation of pressure at these temperatures is impossible. The only possible conclusion that can be made is that $P_{H g}$ lies between 10 and 20atm. The corresponding values of $Δ m_{H g}$ for unit volume are 25 and 50 $m g \cdot c m^{- 3}$ . The typical weight ratio of $m_{H g}$ of Hg, $m_{C d}$ of Cd, and $m_{T e}$ of Te in the solution was 6.65:0.215:18.585 (g). The free space in the synthesis silica ampoule was 6cm³. In order to evaluate the optimal concentration of Hg in the growth solution, we have considered its weight to be equal to 6.50g as an initial quantity. In order to equilibrate this Hg quantity with its partial vapor pressure at 10atm, 150 mg of Hg should be added into the ampoule, whereas 300 mg of Hg should be added in order to attain equilibration at 20 atm. Thus, the total Hg quantity in the first and second cases would be 6.65 and 6.80g, respectively. The arithmetic mean of these quantities (6.50g and 6.80g) is 6.65g. Obviously, the quantity 6.65g may be considered as being dynamically balanced with the Hg vapor at 15atm, which is the arithmetic mean of the extreme pressures of 10 and 20 atm. This quantity will be equilibrated with Hg vapor at 20 atm by adding 150 mg of Hg into the solution. Correspondingly, the removal of 150 mg of Hg from the solution will lead to equilibration at 10 atm. For that reason, we set the basic quantity of Hg to be 6.65 g for calculations. Obviously, changing the Hg content in the solution without changing the Te or Cd content will lead to a change in the consistence ratio. This in turn, will result in changes of $Θ$ and x.

Figure 2 Simulated Θ(ºC) values (solid line) and experimental values (dots).

The results of the calculation of both $Θ = Θ (C_{H g}^{l})$ and $x = x (C_{H g}^{l})$ dependences are plotted in Figure 3. It is clear from figure that for Θ run-to-run reproducibility is $Θ \pm 1.85 ° C$ , while that for $x$ is $x \pm 0.0037$ . The calculated values are found to be in good agreement with experimental data.^1,2

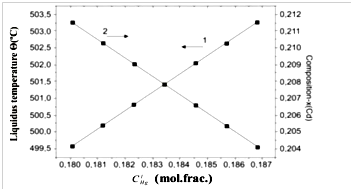
Figure 3 Run-to-run reproducibility of liquidus temperature (1) and epitaxial layer composition (2).

Novel growth apparatus and preparation of LPE layers

The LPE layers of $H g_{1 - x} C d_{x} T e$ (x=0.20–0.22) were grown inside a homemade tipping growth apparatus at 501–470ºC using Te-rich solution ${(H g_{1 - z} C d_{z})}_{1 - y} T e_{y}$ with $z = 0.0545$ and $y = 0.806$ (_L~501ºC) with the ratio of compositions of elemental sources of 6N-purity Hg, Cd, and Te in the liquid phase, $C_{H g}^{l} : C_{C d}^{l} : C_{T e}^{l}$ , of 0.183:0.0106:0.806 (mol frac.) The solutions were synthesized by rocking at 705–710ºC in a sealed silica ampoule, followed by water quenching. The Cd_0,96Zn_0,04Te wafers with (111)B oriented surface were used as substrates. The LPE apparatus providing the residual-melt-drop-free surface is schematically shown in Figure 4. It comprises a quartz ampoule (1), reservoir (2) of solution melt (3), holder (4) for the substrate (5), substrate recess (6), slot (7), opening (8), and pinhole (9) in the holder, quartz wafer (10) with scribe capillary marks (11) on its surface, pin (12) for fixing the quartz wafer, pin (13) for fixing the substrate onto the holder, cap (14) for dipping the substrate, and ampoule plug (15).

Figure 4 LPE growth apparatus.

At the primary stage of the growth process, the previously synthesized ingot of Te-rich ${(H g_{1 - z} C d_{z})}_{1 - y} T e_{y}$ solution was placed into the reservoir, the substrate fixed in the recess (6), the quartz wafer fixed into the slot (7) and joined with the bottom of the substrate. Then the pre-assembled parts of the apparatus were placed into the quartz ampoule and evacuated and sealed. The ampoule with its contents was vertically fixed into the furnace and the liquid solution was produced in the reservoir by heating. When the growth condition was established (at 501ºC), the ampoule was tilted to 180ºC to allow the liquid solution to flow from the reservoir into the vessel and completely immerse the substrate inside. It was kept in this position until the growth of the epilayer was completed (at about 475ºC). At that period, the excess solution was removed from the contact with the substrate by tipping the ampoule back to its original position. The solution flowed from the vessel to the reservoir owing the action of the liquid’s weight, but the surface tension impeded this flow. When the weight of the last droplets of liquid became less than the surface tension force, the droplets trapped at the bottom of the substrate. Since the quartz material is readily wetted by (Hg_1-z Cdz)_1-yTe_y melt, roughness of the surface of the quartz wafer prevented droplet trapping and induced the pulling off of droplets from the bottom of the epilayer.

Characterisation of materials

Surface inspection, x-ray diffraction (XRD), optical transmission are routinely performed to get access to the crystalline and compositional characteristics of the epitaxial structures.The electrical properties of the layer were measured by Van-der Pauw technique using a Bio-Rad system at 77K. The XRD measurement have been made by using Siemens X-RAY Diffraction unit model D-500, kV40, CuKα, A=20mA.

Results and discusson

Figure 4a shows some typical morphological features of as grown epilayers. The epilayer morphology shows terracing patterns and micropits/voids. The later are originated from Te inclusions usually existing in CdZnTe substrates. The typical diameters of Te inclusions are 1-2µm, although sizes up to 100µm are observed in high-pressure and vertical-Bridgman grown CdZnTe wafers.⁶ The microphotograph of cleaved 15µm thick HgCdTe epilayer with planar substrate–epilayer interface is shown on Figure 4b.

Figure 4a & 4b Some typical morphological features (a) and cleaved edge views of typical epitaxial layer (b).

As-grown layers were p-type at 77K owing to the presence of Hg vacancies with a carrier concentration in the range from cm^–3 to cm^–3 and mobility of 240–270cm²V^-1s^-1 due to large stoichiometric deviation towards Te-rich side in this material at around the growth temperatures of 501-475ºC. The desired n-type carrier concentration can be achieved by reducing the Hg-vacancy concentration to this level. There are two ways of achieving this. The excess vacancies can be filed within-diffusion of Hg by heating the o layers under Hg-saturation ambient at around 350ºC or they could be out diffused to the surface under Te-saturation ambient at around 250ºC during 100 hours. We have followed by the first one of those ways and annealing was carried out inside sealed silica ampoule at 280°C for 10 hours. The layers typically became n-type upon a such treatment with a carrier concentration of $(1.0 - 5) \times 10^{14}$ cm^–3 and mobility in the range from 1.0 to $5 \times 10^{4}$ cm² V^-1s^-1.

The XRD spectrum of as-grown and annealed epilayers are shown in Figure 5a & Figure 5b, respectively. Some special diffraction peaks appeared in both XRD spectra at 23.7ºC, 38.5ºC and 46ºC, which gave crystalline HgCdTe a (111), (220) and (311) preferential orientation. As per ASTM standard⁷ those peaks corresponds to the interplanar spacing of 3.74Ǻ, 2.35Ǻ and 1.97Ǻ. This means that the HgCdTe films have a face-centered cubic (fcc) structure, which has the lowest energy on the (111) plane. Apart from those peaks, there are two additional peaks appeared at 22ºC and 28ºC as well. The first one corresponds to the interplanar spacing of 4.15Ǻ little-studied Hg_xTe_z compound phase existing in the epitaxial layer (as per “ICDD PDF-2 Release 2003 of the Powder Diffraction File). The second one, corresponding to the interplanar spacing of 3.18Ǻ wasn’t recognized, however this was annealed out. The intensity of the X-ray diffraction maximum is increased by a factor of 3 after annealing. Meanwhile, it needs to be noted that, despite the position of the peak at 23.7ºC relating to the main cubic phase (111) remained as is after annealing , the diffraction peaks at 38.5ºC and 46ºC relating to the minor phases of (220) and (311) shifted to a higher diffraction angles. A such shift is usually observed when comparing of XRD spectra of of Hg_0.8Cd_0.2Te and Hg_0.7Cd_0.3Te volume single crystals. While increasing of x from 0.2 to 0.3 the interplanar spacing decrease from 6.46Å to 6,40Å respectively. The decrease in 2θ of these peaks may be related to changes in lattice parameters of epitaxial layer. This is because of partial evaporation of Hg from epilayers that lead to decreasing of Hg and increasing of Cdx during annealing and redistribution of their composition.

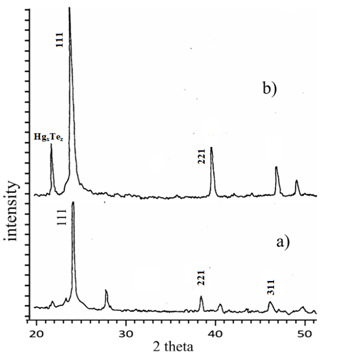
Figure 5 X-ray diffraction patterns of as grown/untreated layer (a) and annealed epitaxial layer (b).

Conclusion

A new empirical expression $Θ = 1144 - 845.4 y + 672.6 z$ for the liquids line of Te-rich corner of Hg-Cd-Te phase diagram is derived which can be used to predict the more exact liquids temperature. A new homemade LPE growth apparatus, preserves the surface of as grown epilayes on residual melt drops is described. It was evaluated that due to inaccuracy in the determination of mercury pressure in a synthesis ampoule the run-to-run reproducibility of θ is $Θ \pm 1.85 ° C$ , while that for x is $x \pm 0.0037$ . The influence of thermal annealing on of XRD spectra is considered.