Biclique cryptanalysis is a generic attack on block cipher to recovering the secret key faster than brute force. In this paperwe use asymmetric independent biclique attack on full round PRESENT. The datacomplexities of our attacks are less than before, which for a fullround attack on PRESENT-80 and PRESENT-128 are 217 plain text-ciphertext pairs The computational complexity is slightly improved

Keywords: PRESENT, Lightweight block cipher, asymmetric independent biclique, key recovery

Biclique cryptanalysis, introduced first in 2011¹ for hash cryptanalysis. After that, Bogdanove in² used this technique and introduced the first biclique attack on full round AES. We can see lots of cryptanalysis results on the other block cipher, such as IDEA, Piccolo, LBlock, SQUARE, KLINE, ARIA, TWINE and HIGHT where proposed.^3–10

Biclique attack is a kind of meet in the middle (MITM) attack that is improved for cryptanalysis block cipher to find the unknown secret key.In a biclique attack; first, all possible secret keys are partitioned into a set of groups of keys. For each group of keys, a bipartite graph is constructed. After that, a partial matching is used to filter the wrong key and get the candidate key for the correct keys .Finally, the valid pair (p,c) is used to get the correct key.

PRESENT has a simple structure and belong to a family of light weight 64-bit block cipher proposed in 2007.¹¹ It supports two key sizes of 80 and 128 bits and denoted by PRESENT-80 and PRESENT-128. A number of biclique attacks on full round PRESENT have been published in.^12–14 In this paper, we use an asymmetric independent biclique attack on full round PRESENT to reduce the data complexity. The data complexity for a full round attack on PRESENT-80 and PRESENT-128 are 2¹⁷ plaintext-ciphertext pairs. By minimizing the number of active sboxes, the computational complexity is slightly improved. A summary of previous works and our result is given in Table 1.

Description of PRESENT

PRESENT is a 64-bit lightweight cipher that consists of 31 rounds with 80 or 128 bits secret key. After the final round, the state is added to XORed with round key to generate the ciphertext. Both versions of PRESENT, have the same structure as shown in Figure 1. But the key schedule is slightly different. See¹¹for detail description of round function. The key schedule expands a secret key 80 or 128 bits to 32 round keys$R{K}^r,$ $r=0,\mathrm{...},31$ with 64 bits each. In PRESENT-80, the 80 bits secret key$K = \left(k_{79},\mathrm{...}, k_0\right)$ , is stored in 80 bits register$SK=(s{k}_{79},\mathrm{...},s{k}_0)$ with $s{k}_i=k_i$ . After that, SK is updated as follow:

$\left(s{k}_{79},\mathrm{...},s{k}_0\right)$=$\left(s{k}_{18}, \mathrm{...}, s{k}_0, s{k}_{79},\mathrm{...},s{k}_{19}\right)$

$\left(s{k}_{79},s{k}_{78},s{k}_{77},s{k}_{76}\right)= sbox\left(s{k}_{79},s{k}_{78},s{k}_{77},s{k}_{76}\right)$

$\left(s{k}_{19},s{k}_{18},s{k}_{17},s{k}_{16},s{k}_{15}\right)= \left(s{k}_{19},s{k}_{18},s{k}_{17},s{k}_{16},s{k}_{15}\right)\oplus \left(r+1\right)$

The 64 leftmost bits of SK selected as 64 bits round keys$R{K}^r,$ for PRESENT-80. The above procedure is repeated until all round keys are constructed. The key schedule of PRESENT-128 is similar and is as follow

$\left(s{k}_{127},\mathrm{...},s{k}_0\right)= \left(s{k}_{66},\mathrm{...},s{k}_0,s{k}_{127},\mathrm{...},s{k}_{67}\right)$

$\left(s{k}_{123},s{k}_{122},s{k}_{121},s{k}_{120}\right) = sbox \left(s{k}_{123},s{k}_{122},s{k}_{121},s{k}_{120}\right)$ >

$\left(s{k}_{127},s{k}_{126},s{k}_{125},s{k}_{124}\right)= sbox \left(s{k}_{127}, s{k}_{126},s{k}_{125},s{k}_{124}\right)$

$\left(s{k}_{66},s{k}_{65},s{k}_{64},s{k}_{63},s{k}_{62}\right)= \left(s{k}_{66},s{k}_{65},s{k}_{64},s{k}_{63},s{k}_{62}\right)\oplus \left(r+1\right)$

The above procedure is repeated, and 64 bits round keys $R{K}^r,$ for PRESENT-128 are constructed as 64 leftmost bits of SK.

Biclique cryptanalysis

In this section, we give a brief overview on biclique cryptanalysis. See² for complete detail of this. In a biclique attack, the biclique can be constructed in plaintext or ciphertext side. Here, we construct a biclique in ciphertext side so the attack is a chosen ciphertext attack, and we need the decryption oracle (for the biclique in plaintext side, the attack is a chosen plaintext attack, and we need the encryption oracle).^15–18

(d₁, d2) -dimensional asymmetric biclique: let f be subciher of cipher E that maps an intermediate state S to the ciphertext $C,f_k\left(S\right) =C$ . The$3-tuple \left[\left\{c_i\right\},\left\{s_j\right\},\left\{K\left[i,j\right]\right\}\right]$ is called $a\left(d1,d2\right)$ -dimensional asymmetric biclique if for all $i=0,1,\mathrm{...},2^{d1}-1$ and $j=0,1,\mathrm{...},2^{d2}-1 ,s_j=f^{-1}{}_{K\left[i,j\right] }\left(c_i\right)$ . The structure (d₁, d2) -dimensional asymmetric biclique is shown in Figure 2.

The four main steps of the biclique attack are:

Key partitioning: An adversary chooses a partition of the key space into groups of key of cardinality 2^(d1+d2) each. A key in a group is indexed as an element of 2^d1×2^d2 matrixes $K\left[i,j\right].$

Constructing a biclique: Independent biclique is an efficient tool for making a biclique. The procedure of constructing the biclique is as follow:

1. Choose a random ciphertext c₀ and compute $s_0$ as $s_0=f^{-1}{}_{k\left[0,0\right]} \left(c_0\right)$
2. Compute $s_i$ as $s_i=f^{-1}{}_{k\left[i,0\right]}\left(c_0\right)$ for $i=1,\mathrm{...},2^{d2}-1.$
3. Compute $c_j$ as $c_j=f_{k\left[0,j\right]}\left(s_0\right)$ for $j=1,\mathrm{...},2^{d1}-1$ .

Partial matching: Partial matching is an efficient way that all keys in a group are tested. By using this method the computational complexity is reduced significantly. Since the biclique is constructed in the ciphertext side, partial matching is performed at the plaintext side. The remaining parts of cipher E are split into the subcipher $g_1$ and$g_2$ ,$E=g_{1}0g_{2}0f$ . We choose the matching variable after subcipher before$g_1$ subcipher $g_2$ The value of matching variable $v$ is calculated in both directions to find the correct key. First, we called on the decryption oracle to obtain plaintext$p_j,j=0,1,\mathrm{...},2^{d1}-1$ . In forward direction, $p_j$ is partially encrypted under key $p_j$ to get$v\left(0,j\right)$ ,$j=0,1,\mathrm{...},2^{d1}-1$ and stored $2^{d1}$ values. After that, in backward direction, is partially decrypted under key$k\left[i,0\right]$ to get,$v\left(0,j\right)$$i=0,1,\mathrm{...},2^{d2}-1$ and store $2^{d2}$ values. For checking the matching,$$v\left(i,j\right)=v\left(i,j\right)$$, we recomputed only those parts that differ from the stored values. Note that by using partial matching, we can reduce the computational complexity significantly.

Rechecking the candidate keys: Since some candidate keys remain in each group of keys, to filter the wrong keys, the valid pair $\left(p,c\right)$ is used to get the correct key. The structure of (d₁, d₂) -dimensional asymmetric biclique cryptanalysis is shown in Figure 3.

Independent asymmetric biclique attack on full round PRESENT-80

In this section, we first construct a $\left(1,3\right)$ -dimension asymmetric biclique on the ciphertext side for round 29-31 of PRESENT-80. The partial secret key used in RK²⁸, RK²⁹, RK³⁰ and RK³¹ are as fallow

$R{K}^{28}:\left(k_{51,\mathrm{...},}{k}_0,k_{79},\mathrm{...},k_{68}\right)$ .

$R{K}^{29}:\left(k_{70,}{k}_{69},\mathrm{...},k_7\right)$ .

$R{K}^{30}:\left(k_9,\mathrm{...},k_0,k_{79},\mathrm{...},k_{26}\right)$

$R{K}^{31}:\left(k_{28},\mathrm{...},k_0,k_{79},\mathrm{...},k_{45}\right)$

The attack consist of four steps:

Key partitioning: The 80 bits key space is partitioned into 2⁷⁶ groups of $2^4$ keys each. The base keys $K\left[0,0\right]$ take all 80 bits of the secret key with 4 bits fixed to zero and the remaining 76 bits take all possible values. In our attack, the differences ${\Delta }_i^k$ are chosen by varying k₅₂ in forward direction, and the key differences ${\nabla }_j^k$ are chosen by varying $\left(k_{36},k_{35},k_{34}\right)$ in backward direction

Constructing a biclique: We use these steps to construct a biclique for each group of keys in the ciphertext side. Let f be subcipher for round 29-31 of PRESENT-80.

Step1. Fix $c_0=0$ and compute $s_0=f^{-1}{}_{k\left[0,0\right]}\left(c_0\right)$

Step2. Decrypt$c_0$ under different keys $K\left[i,0\right]$ to get corresponding states,$s_i$$i=1,2,3$ .The active sboxes are visualized by the blue trail in backward direction in Figure 4. These sboxes should be calculated 2³ times, while the other ones are computed only once; already done in step1.

Step3. Encrypt s₀ under key $K\left[0,1\right]$ to get the corresponding state c₁. The active sboxes are visualized by the red trail in forward direction in Figure 5. These sboxes should be calculated 2 times, while the other ones have already been computed.

Matching: We use partial matching by applying matching with precomputation and recomputation over the remaining round of the cipher to filter the wrong key. Let $g_1$ and $g_2$ be subciphers for rounds 1-15 and rounds 16-28 respectively. We take matching variable v in the bits $v_{63},\mathrm{...},v_{60}$ of the state $v\left(v_{63},\mathrm{...},v_0\right)$ after round 15. Then we detect the right key by computing v in both directions. The correct key is the one that meets in both directions.

Complexity

The cost of a biclique is dominated by the number of sboxes to be calculated, so we count the number of sbox operations in the round transformation and key schedule. Each round of PRESENT-80 together with one round of key schedule takes 17 sbox computations, so the complexity of single encryption equals calculation of $31\times 17=527$ sboxes.

Biclique complexity: For each 2⁷⁶ groups of keys, the following computations should be calculated.

Forward direction complexity: In forward direction, 5 sboxes should be calculated 2 times. The active sboxes are visualized by the red trail in forward direction in Figure 4.

Backward direction complexity: In backward direction, 17 sboxes should be calculated2³=8 times. The active sboxes are visualized by the blue trail in backward direction in Figure 4.The remaining 26 sboxes are calculated once. In total, $5\times 2+17\times 18+26=162$ sboxes should be calculated to construct a biclique.

Matching complexity: For each2⁷⁶ groups of keys the following computations should be calculated.

Forward direction complexity: In forward direction, $2+5+12\times 16+4=203$ sboxes in round transformation and 2 sboxes in key schedule should be calculated 2³ times, and 25 sboxes are calculated only once. The active sboxes are visualized by the blue trail in forward direction in Figure 5. Note that 12 sboxes in round 15 need not to be computated. This procedure is repeated 2 times for all$p_i$ 's, so in forward direction,$2\times \left(2^3\times 205+25\right)=330$ ssboxes should be calculated.

Backward direction complexity: In backward direction, 42 sboxes are calculated once, $1+5+8\times 16+4+1=139$ and sboxes in round transformation and one sbox in key schedule should be calculated 2 times. The active sboxes are visualized by the red trail in backward direction in Figure 5. This procedure is repeated 2³ for all s_j's, so in backward direction,$2^3\times \left(2\times 140+42\right)=2576$ sboxes should be calculated.

Rechecking the candidate keys complexity: Since in each group, 2⁴ keys should be checked and the probability of matching is 2^-4, so $2^4\times 2^{-4}=1$ remaining key candidate should be tested to get the correct key.

In total, the computational complexity of our attack is given by:$2^{76}\left(\frac{162+3330+2756}{527}+1\right)=2^{79.64}$

Data complexity: We need at most 2¹⁷ chosen ciphertexts for performing a biclique attack.

Independent asymmetric biclique attack on full round PRESENT-128: In this section, we describe our attack on PRESENT-128. Since a biclique attack on full round PRESENT-128 is similar to PRESENT-80, we only state our results.

The partial keys used in RK²⁷, RK²⁸, RK²⁹, RK³⁰ and RK³¹ are as fallow:

RK²⁷:$\left(k_{16},\mathrm{...},k_0,k_{127},\mathrm{...},k_{81}\right)$

RK²⁸: $\left(k_{83},\mathrm{...},k_{20}\right)$

RK²⁹ $\left(k_{22},\mathrm{...},k_0,k_{127},\mathrm{...},k_{87}\right)$

RK³⁰:$\left(k_{89},\mathrm{...},k_{26}\right)$

RK³¹:$\left(k_{28},\mathrm{...},k_0,k_{127},\mathrm{...}{k}_{93}\right)$

We construct (1, 3)-dimensional asymmetric biclique on the ciphertext side for round 27-31. The key differences

${\Delta }_i^k$ are chosen by varying k₁₉ in forward direction and the key differences ${\nabla }_j^k$ are chosen by varying $\left(k_{92},k_{91},k_{90}\right)$ in backward direction. The biclique construction is illustrated in Figure 6. Here, f, g₁ and g₂ are subciphers for rounds 28-31, rounds 1-14 and rounds 15-27 respectively. As we see, the${\Delta }_i^k$ affects only 17 bits of ciphertext, and since we use the same value for c₀ in each biclique, the data complexity does not exceed 2¹⁷. We take matching variable v; the least significant 4 bits of the output value after round 14 as shown in Figure 7.

Complexity

Each round of PRESENT-128 together with one round of key schedule takes 18 sbox computations, so the complexity of single encryption equals calculation of $31\times 18=558$ sboxes. The complexity of our attack is given by:

Biclique complexity: In forward direction, 5 sboxes in round transformation and one sbox in key schedule should be calculated 2 times. The active sboxes are visualized by the red trail in forward direction in Figure 6. In backward direction, 15 sboxes should be calculated 2³=8 times. The active sboxes are visualized by the blue trail in backward direction in Figure 6. The remaining 44 sboxes are calculated once. In total $6\times 2+15\times 8+44=176$ sboxes should be calculated to construct a biclique.

Matching complexity: In forward direction,$2+4+11\times 16+4=186$ sboxes in round transformation and one sbox in key schedule should be calculated $2^3$ times and 26 sboxes are calculated once only. The active sboxes are visualized by the blue trail in forward direction in Figure 7. This procedure is repeated 2 times for all$p_{i}i$ 's, so in forward direction$2\times \left(2^3\times 187+26\right)=3044$ , sboxes should be calculated. In backward direction, 43 sboxes are calculated once and $1+4+8\times 16+4+1=138$ sboxes in round transformation should be calculated 2 times. The active sboxes are visualized by the red trail in backward direction in Figure 7. This procedure is repeated 2³ times for all$s_j$ 's, so in backward direction, $2^3\times \left(2\times 138+43\right)=2552$ sboxes should be calculated.

Rechecking the candidate keys complexity: Since in each group, 2⁴ keys should be checked and the probability of matching is 2^-4, so $2^4\times 2^{-4}=1$ remaining key candidate should be tested to reach the correct key.

In total, the computational complexity of our attack is given by:$2^{124}\times \left(\frac{176+3044+2552}{558}+1\right)=2^{127.50}$

Data complexity: We need at most 2¹⁷ chosen ciphertexts for performing a biclique attack.

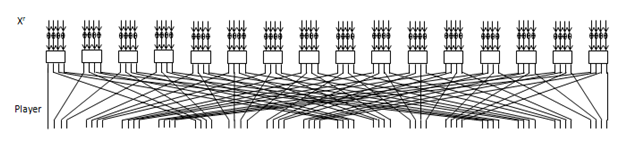
Figure 1 round function of Present.

Figure2 $\left(d_1,d_2\right)$
MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 qadaqadaWdaeaapeGaamiza8aadaWgaaWcbaWdbiaaigdaa8aabeaa k8qacaGGSaGaamiza8aadaWgaaWcbaWdbiaaikdaa8aabeaaaOWdbi aawIcacaGLPaaaaaa@3CA0@ dimensional asymmetric biclique in the ciphertext side.

Figure 3 Representation of  $\left(d1,d2\right)$ -dimensional asymmetric biclique cryptanalysis.

Figure 4 3-round (1,3)-asymmetric biclique for Present-80.

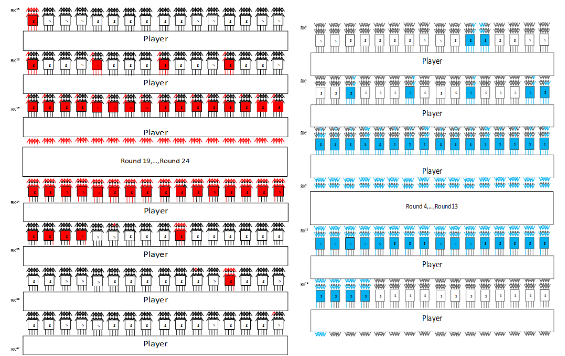
Figure 5 Recompilation in forward and backward direction for Present-80.

Figure 6 4-round (1,3)-asymmetric biclique for Present-128.

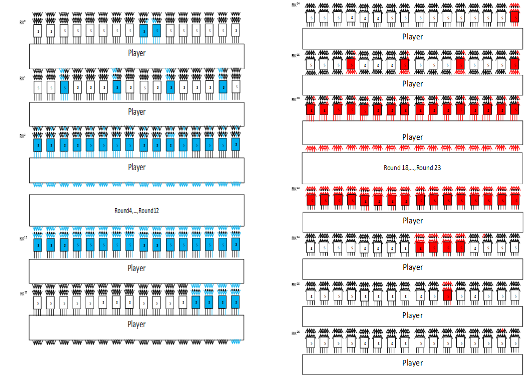
Figure 7 Recompilation in forward and backward direction for Present-128.

In this paper, we present a Biclique cryptanalysis of full round PRESENT with redduced data complexity. . In this paperwe use asymmetric independent biclique attack on full round PRESENT. We construct a asymmetric biclique in ciphertext side for round 29-31 of PRESENT-80 and round 27-31 of PRESENT-128.

The datacomplexities of our attacks are less than before, which for a fullround attack on PRESENT-80 and PRESENT-128 are 2¹⁷ plain text-ciphertext pairs. The computational complexity is slightly improved

None.

The author declares there are no conflicts of interests.

1. Dmitry Khovratovich, Christian Rechberger, Alexandra Savelieva. Bicliques for Preimages: Attacks on Skein-512 and the SHA-2 Family. 2012;1:244–263.
2. Andrey Bogdanov, Dmitry Khovratovich, Christian Rechberger. Biclique Cryptanalysis of the Full AES. Advances in Cryptology – asiacrypt.2011;1:344–371.
3. Dmitry Khovratovich, Gaëtan Leurent, Christian Rechberger. Narrow-Bicliques: Cryptanalysis of Full IDEA. Advances in Cryptology – eurocrypt. 2012;392–410.
4. Yanfeng Wang, Wenling Wu, Xiaoli Yu. Biclique Cryptanalysis of Reduced-Round Piccolo Block Cipher. In Mark Dermot Ryan, Ben Smyth, Guilin Wang, editors. Information Security Practice and Experience. 2012;337–352.
5. Yanfeng Wang, Wenling Wu, Xiaoli Yu, et al. Security on L Block against Biclique Cryptanalysis. Information Security Applications. 2012;1–14.
6. Hamid Mala. Biclique Cryptanalysis of the Block Cipher square. 2014;8(3):207–212.
7. Zahra Ahmadian, Mahmoud Salmasizadeh, Mohammad Reza Aref. Biclique Cryptanalysis of the Full-RoundKLEIN Block Cipher. Iet Information Security.2015;9(5):294–301.
8. Shaozhen Chen, Tianmin Xu. Biclique Attack of the Full ARIA-256. 2012.
9. Mustafa Coban, Ferhat Karakoc, Özkan Boztacs. Biclique Cryptanalysis of TWINE. Cryptology and Network Security. 2012;1:43–55.
10. Deukjo Hong, Bonwook Koo, Daesung Kwon. Biclique Attack on the Full HIGHT. Howon Kim, editor. Information Security and Cryptology – ICISC. 2011;365–374.
11. Andrey Bogdanov, Lars R Knudsen, Gregor Leander, et al. PRESENT: An Ultra-Lightweight Block Cipher. In: Pascal Paillier, Ingrid Verbauwhede, editors. IACR, India; 2007.
12. Kitae Jeong, Hyung Chul Kang, Changhoon Lee, et al. Biclique cryptanalysis of lightweight block ciphers PRESENT, piccolo and led. 2012.
13. Farzaneh Abed, Christian Foler, Eik List, et al. BicliqueCryptanalysis of PRESENTand LED Lightweight Ciphers. 2012.
14. Changhoon Lee. Biclique cryptanalysis of PRESENT-80 and PRESENT-128.J Supercomput. 2014;(70):95–103.
15. Bar On A, Dinur I, Dunkelman O, et al. Improved Analysis of Zorro-Like Ciphers. 2014.
16. Blondeau C, Bogdanov A, Wang M. On the (In) Equivalence of Impossible Differential and Zero-Correlation Distinguishers for Feistel- and Skipjack-Type Ciphers. In: Boureanu I, Owesarski P, Vaudenay S, editors. Applied Cryptography and Network Security. 2014;271–288.
17. Bogdanov A, Geng H, Wang M, et al. Zero-Correlation Linear Cryptanalysis with FFT and Improved Attacks on ISO Standards Camellia and CLEFIA. In: Lange T, Lauter K, Lisonek P, editors. Selected Areas in Cryptography – SAC. 2013;306–323.
18. Donghoon Chang, Mohona Ghosh, Somitra Kumar Sanadhya. Biclique Cryptanalysis of full round AES-128 based hashing modes. In: Dongdai Lin, Moti Yung, Xiaofeng Wang, editors. Inscrypt. 2015;2:3–21.