Data

A retrospective analysis of 1559 subjects was conducted in patients who were evaluated for laser refractive surgery at the Ophthalmology Clinic of the University of South Carolina School of Medicine. Wavefront aberrometry (ZyWave, Technolas Perfect Vision) was performed on subjects aged 18 and above as part of the preoperative evaluation process. To improve overall data quality, six eyes were excluded from the analysis, due to severe dry eye disease or grossly abnormal topography identified by Orbs can II, for a total of 1553 observations.^20,21 Data were extracted to an excel file and then imported to statistical package for the analysis. Data were collected on race, age, refractive error, pupil size and the positive and negative values of each Zernike coefficient representing third, fourth and fifth order HOA. Among these 1553 participants, 44 had missing values in Zernike polynomials. The size of the sample used in the analysis was 1509. The study was approved by Institutional Review Board and in adherence with the Declaration of Helsinki guidelines regarding ethical principles for medical research involving human subjects.

Statistical methods

We utilized four analytical methods each with different goals. First, descriptive statistics (mean and standard deviations (SD) on age, refractive error and Zernike polynomials were calculated to describe the characteristics of our data and compare the subsample (n=1509) with the complete sample (n=1553) to check for consistency. Second, simple linear regression analyses were conducted to estimate the association between each Zernike polynomial and the covariates age and refractive error. Third, we employed methods of Qin and Self,¹⁶ who proposed a model-based clustering method called clustering of regression models (CLM), to group Zernike polynomials that share a similar relationship to the covariates, age and refractive error. Zernike polynomials vary from subject to subject and its variation is partially due to subjects’ pupil sizes. To adjust for this, we performed linear regression analysis on Zernike polynomials with pupil size as the independent variable. The residuals from this regression analysis were pupil-size-adjusted Zernike polynomials and were used in the remaining analyses. We designate, “PSA”, or pupil sized adjusted, throughout the manuscript to remind the reader that pupil size was included in the analyses. This approach represents a commonly used statistical method for adjusting the effect of a variable (i.e., pupil size in our application).²²

Let y be the values of a PSA Zernike polynomial, e.g., horizontal coma. We model the association of y with age and refractive error using a linear regression, which is the essential modeling underlying the CLM method.

$y_k\approx age\times {\beta }_{1k}+refractive error\times {\beta }_{2k}$ (1)

For a PSA Zernike polynomial Y in cluster k, the effect of age on this polynomial is ${\beta }_{2k}$ and the effect of refractive error is ${\beta }_{2k}$ . They describes, on average, how this Zernike polynomial changes with age and how it changes with refractive errors. Equation (1) can also be used to predict or estimate Zernike polynomials of a subject by plugging in the subject’s age and refractive error into (1).

To estimate the coefficients, the expectation-maximization (EM) algorithm was used to infer the cluster assignment of each PSA Zernike polynomial. The number of clusters is determined based on the Bayesian information criterion (BIC) and bootstrapped maximum volume (BMV) aiming to achieve the best and most stable clusters.¹⁸ The number of clusters is expected to have a large BIC value and a small BMV. Bootstrapping method is used to validate the number of clusters.

Fourth, in addition to CLM, we explored the possibility of using quantile regressions as the basis of clustering to improve the quality of clustering. Quantile regressions are suitable to describe heterogeneous associations, in which case linear regressions may produce biased inferences.

There were no statistically significant differences in characteristics between the subsample (n=1509) used in the analyses and the complete sample (n=1553) with respect to age, gender and refractive error (Table 1).

Descriptive statistics for Zernike polynomials are shown in Figure 1 including the mean values and standard deviations of fifteen Zernike polynomials, denoted by Znmf. The first subscript n in the notation denotes the order of aberration, m is the magnitude of the angular frequency and f gives the direction of the angular frequency with 1 being positive and 0 being negative. As indicated by the horizontal zero line, most Zernike polynomials are centered at zero, except for Z₃₁₀ (horizontal coma), Z₃₃₀ (oblique trefoil) and Z₄₀₀ (spherical). The mean of oblique trefoil aberrations is negative and the mean of spherical aberrations is positive, which is consistent with the literature.^9,11,23,24 Furthermore, except for Z₄₀₀, the variations in coma and trefoil aberrations are much higher than in the aberrations at higher levels.

Figure 1 Mean values and standard deviations of 15 higher order Zernike polynomials.

We applied simple linear regressions to each Zernike polynomial to examine its association with age and refractive error, respectively. Through these univariate analyses, some interesting patterns were noteworthy. For instance, both Z₃₁₁ (vertical coma) and Z₃₁₀ (horizontal coma) decreased with increasing age (Figure 2), but their associations with refractive error were opposite. Specifically, Z₃₁₁ increased with refractive error, whereas Z₃₁₀ decreased with increasing refractive error. Without further analysis, it’s unclear whether the coma aberrations (Z₃₁₁ and Z₃₁₀) shared a similar association with age after we adjusted for refractive error and pupil size. Furthermore, as shown in (Figure 2), positive and negative Zernike polynomials are consistent in terms of their association with age and refractive error. Thus in our subsequent analyses, we keep the positive and negative sign of each Zernike polynomial.

Figure 2 Significant relationships between Zernike polynomials (Z₃₁₁ and Z₃₁₀), age and refractive error through simple linear regressions. P-values are included in the parentheses. The significance level is set at 0.05.

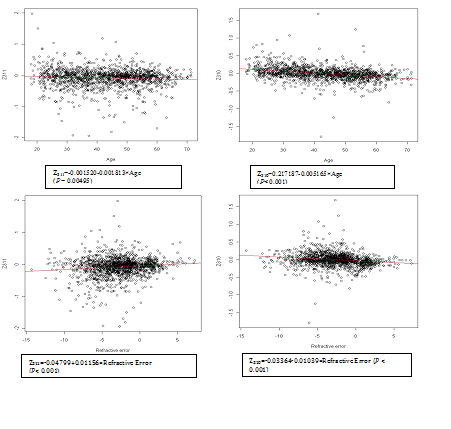
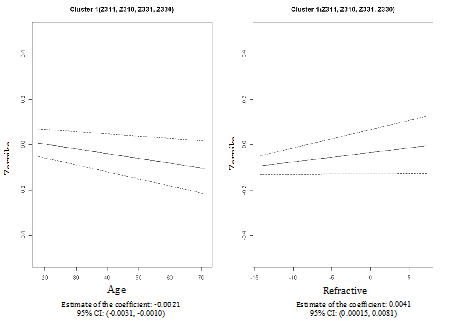
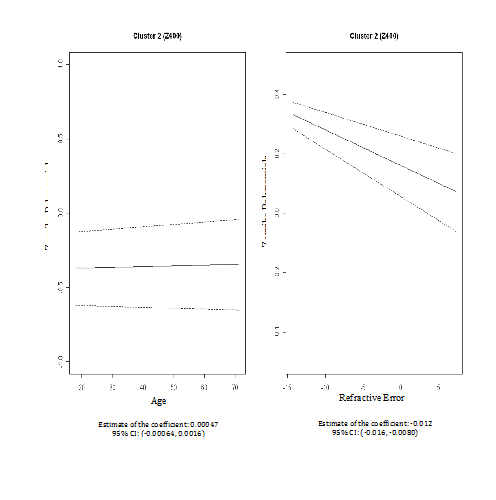
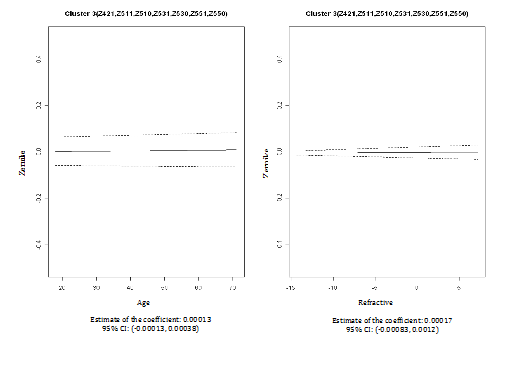
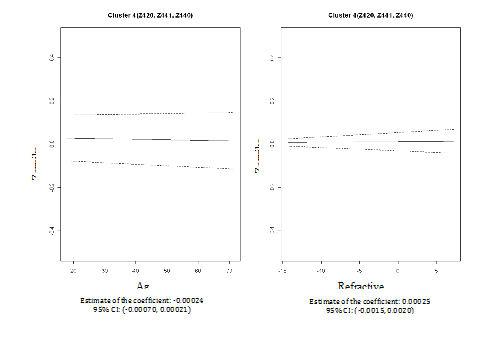
We then performed cluster analyses using the CLM method to examine the pattern similarity between the fifteen PSA Zernike polynomials based on their associations with age and refractive error. Based on the BIC/BMV method, four clusters were identified; and the number of cluster 4 is later confirmed by bootstrapped samples. In the first cluster (Z₃₁₁, Z₃₁₀, Z₃₃₁ and Z₃₃₀), the PSA Zernike polynomials increase with refractive error but decreased with age after adjusting for each other and both patterns were statistically significant (column 2 in Table 2 & Figure 3). The second cluster only includedZ₄₀₀. In this cluster, statistic relationships opposite to that in cluster one were observed; PSA Zernike polynomials were negatively associated (statistically significant) with refractive error, but tend to be positively associated with age (column 3 in Table 2 & Figure 4). In the remaining two clusters, although the patterns were not statistically significant, the PSA Zernike polynomials (secondary astigmatism and secondary coma) in the 3rd cluster tended to increase with both refractive error and age and in cluster 4, it suggested that PSA Zernike polynomials decrease with age but increase with refractive error (columns 4 & 5 in Table 2, Figures 5 & 6). These features in general were consistent with the findings from a preliminary study.²⁵

Figure 3 The trend plots of estimated association of PSA Zernike polynomials with age and refractive errors for cluster 1. The solid line is for the fitted regression line adjusted for the existence of the other variable (age or refractive error) and the dashed lines are the empirical 95% confidence bands.

Figure 4 The trend plots of estimated association of PSA Zernike polynomials with age and refractive errors for cluster 2. The solid line is for the fitted regression line adjusted for the existence of the other variable (age or refractive error) and the dashed lines are the empirical 95% confidence bands.

Figure 5 The trend plots of estimated association of PSA Zernike polynomials with age and refractive errors for cluster 3. The solid line is for the fitted regression line adjusted for the existence of the other variable (age or refractive error) and the dashed lines are the empirical 95% confidence bands.

Figure 6 The trend plots of estimated association of PSA Zernike polynomials with age and refractive errors for cluster 4. The solid line is for the fitted regression line adjusted for the existence of the other variable (age or refractive error) and the dashed lines are the empirical 95% confidence bands.

In this article, linear regressions were applied in the cluster analysis. However, some interesting patterns observed in our data are noteworthy. We used the association of Z₃₁₁ with refractive error as an example to illustrate our observation (Figure 7). We fitted the data with regression lines using two different methods. The solid black line was the linear regression line drawn by regression toward the mean, which is the basis of the clustering method used in our work. The other dashed lines were from quantile regressions. As shown in the Figure 7, the linear regression line (solid black line) roughly overlapped with the median regression line (dashed black line). However, it was clear to see that the associations of Z₃₁₁ with refractive error were different at different quantiles i.e., different for different populations, which required further investigation.

Figure 7 Plot of Z₃₁₁ with fitted regression lines using regression toward the mean and quantile regressions. The black line is from regression toward the mean, and other lines are from quantile regressions. The quintiles are indicated in the figure legend.

In this study, fifteen pupil-size-adjusted (PSA) Zernike polynomials were grouped into four clusters via the method of clustering through regression. PSA Zernike polynomials within each cluster shared the same patterns with respect to age and refractive error. Significant associations of Zernike polynomials with age and refractive were only observed in the clusters formed by the third order (coma Z₃₁₁, Z₃₁₀ and trefoil Z₃₃₁ and Z₃₃₀) and fourth order polynomials (spherical aberration Z₄₀₀).The study population included in this study was normative without evidence of ocular diseases.

Understanding the complexity of the individual Zernike polynomials by disentangling them in clusters using the analytical methods applied herein may help to clarify the associations of HOA with age and refractive error and more broadly, may lead to a deeper understanding of the effect of ocular conditions and diseases that affect the visual pathway. Compared to other HOA studies, the advantage of this work is 1) the relatively large sample in which cluster analysis is used to describe HOA in a normative population, 2) a systematic analysis on the associations of HOA with age and refractive error that provides more detail than an assessment using the summary statistic, RMS and 3) the ability to identify cluster patterns to estimate and predict Zernike polynomials for an individual patient representative of a normative database and to utilize clustering analysis to better describe ocular pathological conditions that affect HOA. This may lead to greater relevance of aberrometry in the early diagnosis and improved quantification of pathological conditions, such as keratoconus, dry eye disease, or cataract.

Other pattern analyses have been applied to understand Zernike polynomials for different populations such as neural network decision trees and classification decision trees.² These decision trees classify subjects into different groups based on their Zernike polynomials with each group representing a specific disease status, e.g., keratoconus. However, age, refractive error and pupil size are confounded and not adjusted in the process of tree constructions, which can possibly result in misleading conclusions. Our proposed clustering methods, on the other hand, estimate the effects of age and refractive error with pupil size adjusted while identifying the patterns. Future work may be to introduce the clustering process into the neural network decision trees or classification trees to more effectively and meaningfully group subjects according to disease-specific HOA.