Yield stability has always been considered as an important topic in plant breeding but will be more concern by the continued variation in climatic condition. The phenotype of an individual is a mixture of both genotype (G) and environment (E). As a consequence of G × E interaction, crop varieties may not show uniform performance across different environments. The term genotype refers to the genetic makeup of an organism while environment refers to biophysical factors that have an effect on the growth and development of a genotype.1 The G × E study is especially important in countries with various agro-ecologies. Significant G × E interaction is a consequence of variations in the extent of differences among genotypes in diverse environments (called as a qualitative or rank changes) or variations in the comparative ranking of the genotypes (called as a quantitative or absolute differences between genotypes)2–4
Stability definition
All performance stability, phenotypic stability, and adaptation terms are usually used in total various meanings and different senses and explanations are introduced over the years.5,6 In a static mean of stability defined by Becker and Leon,6 a stable genotype is the one possessing a constant performance irrespective of any changes in environmental conditions. According to Peterson et al.,7 the optimal genotype stability definition and response for quality parameters varies relatively from that conventionally used to characterize yield stability. For breeders, stability of quality properties is important from the points of changing genotypes ranks’ throughout environments and influences selection efficiency. For end-users, such as millers and bakers, stability in quality properties of genotypes is more important, irrespective of genotypes rank changes. However, as pointed out by Grausgruber et al.,8 the quality of a genotype often behaves similar to other quantitative characters to desirable and undesirable environmental conditions. As a result, a genotype is regarded stable if it has a low contribution to the G × E interaction.
Basic concepts
In the final stage of plant breeding, the new varieties are grown under different seasons of the year, environments, climatic and soil conditions.6,9 Environments and seasons, in the role of different conditions, are specified to be a single factor for environmental conditions. The most commonly used designs in these experiments are randomized complete blocks and incomplete block designs. For the latter, owing to the large number of genotypes, lattice designs are usually used. In all experiments, plant breeders usually focus on modeling the genotype means estimated in the jth environment. Therefore, one may consider the linear model:
(1)
where:
is the observed mean of the
genotype at the
environment, for
, and
is the overall mean of the
genotype;
is the effect of the
genotype,
represents the effect of the
environment,
is the effect of interaction between
genotype and
environment,
is the mean error related to the observed
The
interaction (term
in equation 1) can be explained as the differential yield response of a genotype to environments. As a direct consequence of
interaction, the approximate performances of two genotypes vary with the environment stimuli. As a result, one of the most significant goals of the phenotype stability analysis is to distinguish the genotypes whose phenotypic performance remains constant while the environmental conditions change. In the presence of
interaction, these analyses make sense.10 Radiation, water, and nutrients availability are among the factors which strongly influence crop growth and yield11 therefore, the components of phenotypic variance may often rank as follows:12–20
In contrast to the above ranking, in a study by Puttha et al.,21 the genotype contributed to a large proportion of variation in inulin content and fresh tuber yield, whilst  and environment had a smaller contribution to discrepancies. The difference in contrast is feasibly largely because of materials used and environments’ conditions. In other studies, it was observed that the G × sowing seasons (SS) interaction was less important than the
year interaction.22 These results show that the evaluation of genotypes based on several environments and years is more important than the evaluation for the two seasons.
and environment had a smaller contribution to discrepancies. The difference in contrast is feasibly largely because of materials used and environments’ conditions. In other studies, it was observed that the G × sowing seasons (SS) interaction was less important than the
year interaction.22 These results show that the evaluation of genotypes based on several environments and years is more important than the evaluation for the two seasons.
Illustration of effect
To show the environmental effect, the 2 genotypes called A and B, are tested in two environments (E1 and E2) in Figure 1. Figure 1a indicates the presence of an interaction effect in which genotype A is superior to genotype B in E1 but has the lowest mean in E2. Figure 1 b shows the absence of interaction.
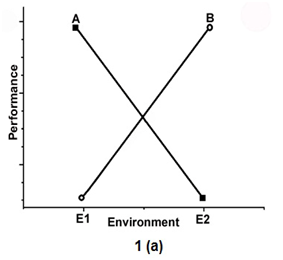
Figure 1a Indicates the presence of an interaction effect in which genotype A is superior to genotype B in E1 but has the lowest mean in E2.
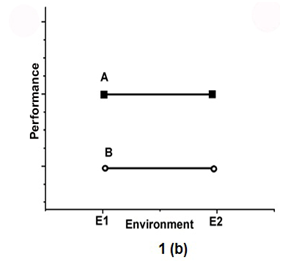
Figure 1b Shows the absence of interaction.
Methods for estimating phenotypic stability
The economic significance of stability for the cultivation of a genotype was first identified by Roemer [1917, cited in 8] who used the variance across environments as a parameter for yield stability. This stability parameter follows a biological/static sense implicating that a stable genotype is recognized as the one having small variance across the tested environments.6 Therefore, to estimate the static phenotype stability of the
genotype, the following equation can be used:
=
(2)
where
is the performance of the
genotype in the
environment,
is the mean performance of the
genotype and
is the number of environments.
If the sample estimate is not significantly different from zero, a genotype is then recognized to be stable which means that environmental changes will not influence the genotype performance. However, this type is rarely a favored feature of crop landraces, inasmuch as genotypes with high phenotypic stability obtained through the environmental change have low yield. As a result, this method does not desired by plant breeders to evaluate the phenotypic stability of the genotype performance, or other related random variables. Although, it is helpful to evaluate the phenotypic stability of the traits that should retain their levels such as stress characters like winter hardiness, qualitative traits, or disease resistance.23 In contrast, if a genotype response to environmental changes has no deviation from the general response of all genotypes in the trial, it is called as dynamic or agronomic stability. The dynamic concept of stability is useful for quantitative traits such as yield.23
Using the dynamic concept of stability, Wricke’s25,25 model is the simplest method to evaluate the stability. Wricke25,25 suggested the ecovalence (W2i) concept as the ratio of the interaction sum of squares contributed by each genotype to the
interaction sum of squares. In other words, the ecovalence of the
genotype is its interaction with the environments, squared and summed across environments, and expressed as
(3)
Where
is the mean performance of the
genotype in the
environment and
and
are the genotype and environment mean deviations, respectively, and
is the overall mean. For this reason, genotypes with a low
value have smaller deviations from the mean across environments and are therefore more stable. Based on Becker and Leon,6 a genotype with
is considered stable.
Shukla26 proposed the variance component of each genotype across environments as another relevant measure of phenotypic stability. It measures stability rather than performance. According to Shukla26 stability variance
sum of squares is partitioned into components, one corresponding to each genotype and estimated as
(4)
Where G is number of genotypes, E is number of environments,
is the mean yield of the
genotype in the
environment,
is the mean of the
genotypein all environments,
is the mean of all genotypes in
environments and
is the overall mean.
If the stability variance of a genotype was equal to the environmental variance
, then genotype is identified as stable. A slightly large value of
will therefore illustrate more instability of the
genotype. Significant
value’s also shows that a genotype’s performance throughout the environments was unstable. Genotypes with a non significant or negative
would be regarded stable throughout the environments.26 Since σ2i is the difference between two sums of squares, negative
may sometimes occur which can be considered as equal to zero in such conditions.26 It is also important to note that
cannot be computed from unbalanced data.27
The level of correlation among different stability parameters represents whether one or more parameters should be used for cultivar performance prediction, and also gives breeder the right to choose the best stability parameter(s) to fit the sense of stability.28 Shukla26 stability variance is a linear combination of deviation mean squares, in other words the Wricke24,25 ecovalance. Significant positive correlation between
and
was found in different studies (Table 1) which indicates that
and
are equivalent in ranking genotypes for stability [29-33]. As a result, it is adequate and acceptable to use one of the two statistics solely.34 However, in a study by Kang et al.,35 Shukla26 method was preferred to Wricke24,25 for estimating the yield stability of sugar cane cultivars. Contrary to the results of previous studies (Table 1), Akcura et al.36 reported a significant negative association (-0.88, P < 0.05) between
and
.
The main type of stability analysis called joint regression analysis or joint linear regression (JLR) was termed by Freeman.37 It helps to estimate whether the genotypes have characteristic in a linear responses to environmental changes. The interaction sum of squares is partitioned into two parts: one describes the heterogeneity of linear regression coefficient
whereas the second represents a deviation
:
(5)
and therefore
(6)
Where
is the environmental index,
is the regression coefficient that measures the response of the genotype of varying environments,
stands for the deviation from regression of the
genotype at the
environment, and the remaining stands as specified in equation 1. The joint regression analysis approach was first introduced by Yates and Cochran38 and was later modified by Finlay and Wilkinson39 and Eberhart & Russell40 which is a widely used method nowadays.
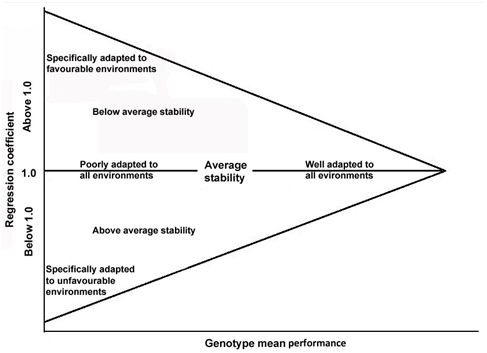
Figure 2 Genotype regression coefficients plotted against genotype performance, adapted from Finlay and Wilkinson.
39
Correlation Type |
Crop Species |
References |
Correlation between
and
|
|
|
Positive correlation |
Common bean, Phaseolus vulgaris L. |
43 |
Negative correlation |
|
Correlation between
and |
|
43 |
Positive correlation |
Common bean, Phaseolus vulgaris L. |
Negative correlation |
|
Correlation between
and |
|
|
Positive correlation |
Chickpea, Cicer arietinum L.
Durum wheat, Triticum durum Desf.
Tea, Camellia sinensis |
83
84
42 |
Correlation between
andCV |
|
|
Positive correlation |
Durum wheat, Triticum durum Desf.
Durum wheat, Triticum durum Desf.
Lentil, Lens culinaris Medik
Pea, Pisum sativum L. |
85
84
71
56 |
Negative correlation |
|
|
Correlation between
and
|
|
|
Positive correlation |
Chickpea, Cicer arietinum L.
Common bean, Phaseolus vulgaris L. |
83
43 |
Negative correlation |
|
|
Correlation between
and
|
|
|
Positive correlation |
|
|
Negative correlation |
Common bean, Phaseolus vulgaris L.
Lentil, Lens culinaris Medik |
43
71 |
Correlation betweenand |
|
|
Positive correlation |
Barley, Hordeum vulgare L.
Chenopodium spp.
Chickpea, Cicer arietinum L.
Common bean, Phaseolus vulgaris L.
Cowpea, Vigna unguiculata [L.] Walp
Durum wheat, Triticum durum Desf.
Lentil, Lens culinaris Medik
Maize, Zea mays L.
Pea, Pisum sativum L.
Pea, Pisum sativum L.
Rapeseed, Brassica napus L. |
91
92
83
43
93
84
71
55
94
56
95 |
Negative correlation |
Durum wheat, Triticum durum Desf. |
36 |
Correlation betweenand |
|
|
Positive correlation |
Durum wheat, Triticum durum Desf.
Sorghum, Sorghum bicolor (L.) Moench |
36
96 |
Negative correlation |
|
|
Correlation between
and |
|
|
Positive correlation |
Soybean, Glycine max (L.) Merr. |
97 |
Negative correlation |
|
|
Correlation betweenand |
|
|
Positive correlation |
Chickpea, Cicer arietinum L.
Common bean, Phaseolus vulgaris L.
Durum wheat, Triticum durum Desf.
Durum wheat, Triticum durum Desf.
Lentil, Lens culinaris Medik
Maize, Zea mays L.
Pea, Pisum sativum L.
Pea, Pisum sativum L.
Popcorn, Zea mays L.
Rubber tree, Hevea brasiliensis
Sorghum, Sorghum bicolor (L.) Moench
Soybean, Glycine max (L.) Merr.
Winter Rapeseed, Brassica napus L. |
83
43
84
85
71
55
57
56
48
86*
96
41
45 |
Negative correlation |
Durum wheat, Triticum durum Desf. |
36 |
Correlation betweenand |
|
|
Positive correlation |
Common bean, Phaseolus vulgaris L.
Durum wheat, Triticum durum Desf.
Lentil, Lens culinaris Medik
Maize, Zea mays L.
Pea, Pisum sativum L.
Pea, Pisum sativum L.
Tea, Camellia sinensis |
43
36
71
55
94
56
42 |
Negative correlation |
|
|
Correlation betweenand |
|
|
Positive correlation |
Chickpea, Cicer arietinum L.
Lentil, Lens culinaris Medik
Sorghum, Sorghum bicolor (L.) Moench |
83
71
96 |
Negative correlation |
Winter Rapeseed, Brassica napus L. |
45 |
Correlation betweenand
|
|
|
Positive correlation |
Lentil, Lens culinaris Medik |
71 |
Negative correlation |
|
|
Correlation betweenand
|
|
|
Positive correlation |
Durum wheat, Triticum durum Desf.
Sorghum, Sorghum bicolor (L.) Moench |
36
96 |
Negative correlation |
Chickpea, Cicer arietinum L.
Common bean, Phaseolus vulgaris L.
Lentil, Lens culinaris Medik |
83
43
71 |
Correlation between
and CV |
|
|
Positive correlation |
Pea, Pisum sativum L. |
56 |
Negative correlation |
|
|
Correlation between
and |
|
|
Positive correlation |
Durum wheat |
67 |
Negative correlation |
|
|
Correlation between and |
|
|
Positive correlation |
Lentil, Lens culinaris Medik |
71 |
Negative correlation |
|
|
Correlation between and |
|
|
Positive correlation |
|
|
Negative correlation |
Chickpea, Cicer arietinum L.
Durum wheat, Triticum durum Desf.
Popcorn, Zea mays L.
Rye
Maize, Zea mays L.
Timothy, Phleum pratense L. |
83
85
48
69
98
70 |
Correlation betweenand
|
|
|
Positive correlation |
Sorghum, Sorghum bicolor (L.) Moench |
96 |
Negative correlation |
Chickpea, Cicer arietinum L.
Common bean, Phaseolus vulgaris L.
Durum wheat, Triticum durum Desf. |
83
43
36 |
Correlation between
and
|
|
|
Positive correlation |
Durum wheat, Triticum durum Desf. |
36 |
Negative correlation |
Common bean, Phaseolus vulgaris L. |
43 |
Correlation between
and |
|
|
Positive correlation |
Sorghum, Sorghum bicolor (L.) Moench |
96 |
Negative correlation |
|
|
Correlation between
and |
|
|
Positive correlation |
Lentil, Lens culinaris Medik |
71 |
Negative correlation |
|
|
Correlation between andCV |
|
|
Positive correlation |
Durum wheat, Triticum durum Desf.
Durum wheat, Triticum durum Desf.
Durum wheat, Triticum durum Desf.
Maize, Zea mays L.
Soybean, Glycine max (L.) Merr.
Sugar beet |
36
84
85
55
41
99 |
Negative correlation |
|
|
Correlation between and
|
|
|
Positive correlation |
|
|
Negative correlation |
Durum wheat, Triticum durum Desf. |
85 |
Correlation between
and |
|
|
Positive correlation |
Rubber tree, Hevea brasiliensis |
86* |
Negative correlation |
|
|
Correlation between and |
|
|
Positive correlation |
Rubber tree, Hevea brasiliensis |
86* |
Negative correlation |
Durum wheat, Triticum durum Desf. |
85 |
Correlation between andCV |
|
|
Positive correlation |
Maize, Zea mays L. |
55 |
Negative correlation |
|
|
Table 1 Relationship among different stability parameters.
*Vigor characteristic,
: environmental variance,: ecovalence,
: Shukla’s stability variance, CV: coefficient of variability,
: coefficient of determination, : regression coefficient,
: superiority measure,: deviation from regression mean squares,
: Perkins and Jinks’s stability parameter.66
The regression coefficient was introduced by Finlay and Wilkinson39 as the regression of the mean of
genotype in
environment on the mean performance of all genotypes in that environment and is expressed as
(7)
where
is the performance of the
genotype in the
environment,
Is the mean performance of the
genotype, and
is the mean performance of the
environment,
is the overall mean and E is the number of environments. The regression coefficient
mainly indicates the adaptation of a genotype to several environments and also describes the linear response between environments. However, it does not reflect stability, crop performance, or stability extension.40,41
As it could be seen in Figure 2, a genotype which has a regression line above that for overall mean performance is regarded to have high performance stability and is able to adapt to all environments. As the productivity of the environment improves, the performance of such genotype would increase. A genotype is considered to have adaptation to a specific environment if its regression line crosses that for overall mean performance. A genotype is regarded to have low performance adaptability across environments if its regression line placed below that for the overall mean performance.39 The slope of regression line showed a positive association with yield potential in different studies16,32,42–46 which means that high yielding genotypes have larger values for bi which are particularly adapted to environments with favourable growing condition. Therefore, such genotypes, when cultivated in poor environments would show less than optimal performance but when cultivated in optimal environments, they could achieve maximum performance.
Altay47 suggested that Finlay and Wilkinson39 method is a preferable method for the assessment of specific or wide adaptation of genotypes compared with Wricke24,25 ecovalence.
Eberhart and Russell40 suggested using the mean of squared deviations from regression
as a measure for stability and a stable genotype is the one has a small deviation from regression mean squares (equation 8).
(8)
where all components have their usual meanings.
According to Eberhart and Russell40 model, genotypes are grouped based on their variance of the regression deviation (either equal or not to zero). A genotype with variance in regression deviation equal to zero is highly predictable, whilst a genotype with regression deviation more than zero has less predictable response [48]. Although, regression model is displayed to be the most useful approach for geneticists37,48–51 but authors have found a number of statistical and biological restrictions and criticisms.
One of the drawbacks of this analysis is that the mean of all genotypes in each environment is considered as a measure of the environmental index and is used as an independent variable in the regression. According to the regression analysis assumptions, no independence can be among the variables, particularly when the number of genotypes is less than 15.6,52 In addition, the variation in regression coefficient result is most often so small which makes it difficult to rank the genotypes for stability and adaptability. Regression analysis should be used with caution when only a few low or high performance sites are included in the analysis;51,52 since the genotype fit may be determined greatly by its performance in a few extreme environments, it leads to the generation of misleading results.
A strong positive relationship between
and
was found in studies on durum wheat, lentil, maize, and pea (Table 1) and also between
and
for durum wheat, lentil, maize, pea, popcorn, sorghum, and soybean cultivars (Table 1). Jowett53 concluded that the Eberhart and Russell40 method, which uses an arithmetic scale, was more explicit than the Finlay and Wilkinson procedure, which uses a logarithmic scale. Stability parameters such as
,
, and
were found to be useful in assessing the phenotypic stability of field genotypes.3454–57 Marjanovic-Jeromela et al.45 found a negative correlation between
and
which indicates that either of these two methods could be used independently from each other without influencing accuracy of estimation.
Joint regression and QTL mapping
Two possible genetic mechanisms including the allelic sensitivity and gene regulation models are proposed for supporting stability.58,59 In the first model and in direct response to the environment, the constitutive gene regulates itself through the activation of different alleles in various environments.
Regardless of how stability is expressed or measured, one of the most important questions for a stability parameter is whether it is genetic.60 Two possible genetic mechanisms are proposed for underpinning stability;58,59 the allelic sensitivity model, which suggests that the constitutive gene is regulated itself in direct response to the environment through the activation of different alleles in various environments. The gene regulation model implies that one or more regulatory loci are under the direct influence of the environment and the constitutive gene is switched on or off by the regulatory gene. Collocation of QTLs (a segment of DNA that influences a quantitative trait) illustrating
interactions and QTLs for stability parameters would support the allelic sensitivity model,59,61 whilst QTLs for stability parameters detected in regions other than those for the trait would imply a regulatory model.62,63 Joint regression analysis is widely used in quantitative genetics to analyze QTL × environment interaction.59,64 Previous studies found that the deviation from regression is not under genetic control,59,65 which is in contrary to the findings of Kraakman et al.61
Perkins and Jink66 introduced a statistical analysis to measure non linear sensitivity to the environmental variations by considering the interaction component of each genotype as a linear function of the additive environmental component. In this model, the deviation from the regression line of each environment is considered as a fixed effect and a genotype with
and
is regarded as stable. The
-values38–40 have a mean of unity, while the
-values6,26 have a mean of zero.
In a study by Annicchiarico and Mariani,67 9 wheat lines were grown at six Italian locations for three seasons. Positive correlation between
-values and
indicated lines adaptability with generally low yield stability.
Lin and Binns68 proposed the superiority measure
of the
genotype as the performance difference comparison among a set of genotypes compared with a reference genotype with the maximum performance within each environment:
(9)
Where
is the average performance of the
genotype in the
environment,
is the genotype with maximum performance among all genotypes in the
environment, and
is the number of environments.
Small
value’s indicates less distance between the
genotype and the genotype with maximum performance and the better the genotype.69,70 This explanation of superiority is compared to the breeder’s purpose, because a superior genotype should be placed among the most productive genotypes across environments.
Although, Lin and Binns68 method is seldom used in different studies but it does not have restrictions of the regression model. In this method, the stability statistics are on the basis of both the average genotype effects and
interaction effects, and each genotype is compared only with the one maximum performance at each environment.52 It also seems to be extremely a measure of genotype performance rather than stability.
displayed the largest deviation from all the other procedures, including negative and significant rank correlation coefficients with
compared to the other procedures (Table 1). Positive correlations between yield values and
were found.46,71
Francis and Kannenberg72 proposed coefficient of variation (CV) as a stability measure as follows:
(10)
where evi is the sum of squares of interaction effects and the remaining stands as specified in equation 3. Although CV is a simple method and repeatedly used by breeders and other workers but it has its own limitation’s. While comparing genotypes across high and low yielding environments if the mean and standard deviation do not vary in a parallel way as performance increases, a bias would happen, whereby high means result in low CV and low means in high CVs.73
In different studies, Francis and Kannenberg72 method was found most useful and informative compared with other stability parameters.3474,75 A positive correlation was also found between
and CV.41 Pinthus76 introduced coefficient of determination
method to estimate stability of genotypes (equation 11). He suggested
as an alternative to the deviation mean squares, since
is strongly related to .77
Coefficient of determination:
(11)
In comparison with CV, is a more robust index and is shown to be a better platform compared with
since its value ranges between zero and one.78 Higher values are desired because illustrate favourable responses to environmental variations. In general, if the CV is below 15% and is above 70%, the experiment is valid. Mekbib43 found a significant positive correlation between and yield values.
Multivariate approaches for stability analysis
There are different multivariates models for stability analysis among which the two most commonly used approaches are:
- The additive main effects and multiplicative interaction (AMMI) method which gives information on main and interaction effects in addition to a biplot. It is specifically efficient for illustrating adaptive responses79,80 and is recently suggested as a replacement to the joint regression analysis for most of the breeding programmes.81 However, it needs greater number of genotypes, small number of replications, and also several years for evaluation in comparison with other models. Furthermore, the complexity of the result’s interpretation compared with Eberhart and Russell40 models should be highlighted. In addition, AMMI is incapable to found close relationship between high performance and stability.82 In a study by Purchase,31 joint regression, Wricke24,25 and AMMI methods were found to be more useful in assessing the stability of durum wheat genotypes. Highly significant rank correlation was found among
,
, and AMMI stability values in chickpea,83 durum wheat,84,85 pea,56,57 and rubber tree.86 Also positive correlations were found between AMMI and other stability parameters such as 56 and .86
- The biplot technique named ‘GGE biplot’ was developed by Yan et al.87 to represent genotype main effects and interaction graphically. Although biplot analysis is not sensitive to the number of genotypes but it is the best predictor of genotype stability for a small number of genotypes.88 In a study by Alwala et al.,17 evaluating 24 maize hybrids at 24 environments across 7 Midwestern states in 2007, biplot analysis was found better than Eberhart and Russell joint regression analysis in identifying stable and high yielding genotypes.
Although AMMI and GGE are equivalent in achieving predictive accuracy, the AMMI method is considered superior to GGE for evaluating yield trial data,89 because it shows genotype main effects, environment main effects and interaction effects, whilst the GGE biplot only displays G and effects.90-99


![]() and environment had a smaller contribution to discrepancies. The difference in contrast is feasibly largely because of materials used and environments’ conditions. In other studies, it was observed that the G × sowing seasons (SS) interaction was less important than the
year interaction.22 These results show that the evaluation of genotypes based on several environments and years is more important than the evaluation for the two seasons.
and environment had a smaller contribution to discrepancies. The difference in contrast is feasibly largely because of materials used and environments’ conditions. In other studies, it was observed that the G × sowing seasons (SS) interaction was less important than the
year interaction.22 These results show that the evaluation of genotypes based on several environments and years is more important than the evaluation for the two seasons. 

