Statistical modeling of the number of deaths of children in Bangladesh

doi:10.15406/bbij.2014.01.00014

eISSN: 2378-315X

Biometrics & Biostatistics International Journal

Research Article Volume 1 Issue 3

Statistical modeling of the number of deaths of children in Bangladesh

Moshed Alam,^1,2 Manzur Rahman Farazi,^1,2 Joseph Stiglitz,² Munni Begum²

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

¹Department of Statistics, Jahangirnagar University, Bangladesh
²Department of Mathematical Sciences, Ball State University, Indiana, USA

Correspondence: Munni Begum, Department of Mathematical Sciences, Ball State University, Indiana, USA, Tel 1-765-285-8673

Received: November 12, 2014 | Published: December 11, 2014

Citation: Alam M, Farazi MR, Stiglitz J, et al. Statistical modeling of the number of deaths of children in Bangladesh. Biom Biostat Int J. 2014;1(3):64‒73 DOI: 10.15406/bbij.2014.01.00014

Download PDF

Abstract

Efforts to reduce the number of children’s death in developing countries through health care programs focus more to the prevention and control of diseases than to determining the underlying risk factors/predictors and addressing these through proper interventions. This study aims to identify socioeconomic and demographic predictors of the number of children’s death to women aged 12-49 from the Bangladesh Health and Demographic Survey (BDHS) administered in 2011. The number of children’s death in a family is a non-negative count response variable. The average number of children’s death is found to be 28 per 100 women with a variance of 44per 100 women. Thus Poisson regression model is not a proper choice to predict the mean response from the BDHS data due to the presence of over-dispersion. In order to address over-dispersion, we fit a Negative Binomial Regression (NBR), a Zero-Inflated Negative Binomial Regression (ZINBR) and a Hurdle Regression (HR) model. Among these models, ZINBR fits the data best. We identify respondent’s age, respondent’s age at 1^st birth, gap between 1^st birth and marriage, number of family members, region, religion, respondent’s education, husband’s education, incidence of twins, source of water, and wealth index as significant predictors for the number of children’s death in a family from the best fitted model. Identification of the risk factors of the number of children’s death is an important public health issue and should be carried out correctly for the much needed intervention.

Keywords: number of child deaths, predictors, NBR, ZINBR, HR

Abbreviations

BDHS, bangladesh health and demographic survey; NBR, negative binomial regression; ZINBR, zero-inflated negative binomial regression; HR, hurdle regression

Introduction

Reduction of child mortality is one of the prime objectives of the south eastern Asian nation Bangladesh. Bangladesh has made impressive progress in health and human development since its emergence as an independent nation in 1971.¹^,² Although the country achieved significant improvement in public health and in controlling the morbidities and mortalities from preventable diseases, child mortality is still a major public health issue. Every year between 8 and 11 million children die worldwide before reaching their fifth birthday.³ The underlying cause for 60% of the deaths of children under the age five in Bangladesh is malnutrition.³^,⁴ The primary objective of the current study is to identify socioeconomic and demographic risk factors/predictors of the number of children"s death for women aged 12-49 from the Bangladesh Health and Demographic Survey (BDHS) administered in 2011. It is useful for the policymakers to have a set of risk factors of the number of children"s death in order to develop guidelines and address these risk factors with proper intervention. Framing proper guidelines and policies to reduce child mortality will insure the sustainability of achieving the Millennium Development Goal (MDG)⁴ relating child mortality.

In terms of demographic and socioeconomic determinants, maternal age and education are found to be strongly correlated with child morality.¹^,⁵^–¹¹ Although the relationship between parental education and the number of children"s death is complex, a number of studies have illustrated that children of less educated parents tend to have a higher mortality rate than children of well-educated ones.⁶^,⁹^,¹⁰^–¹³ Parental education, more importantly maternal education, is identified as a strong predictor of child morality.⁵^,⁹^–¹¹ Other determinants of child mortality may include rural-urban residency,¹^,³^,¹¹^,¹³^,¹⁴ number of children in a household,¹^,³^,¹⁴ water source¹^,¹² and toilet facility.¹^,⁵^,¹¹^,¹⁴ Most of these studies related to children"s mortality and children"s survival used proportional hazards models and multivariable logistic regression.⁸ For instance, Bhuiya et al.⁸ applied a proportional hazard models to study strong relationships with childhood mortality in Bangladesh. Majumder et al. ⁹ used multivariate analysis to identify socioeconomic and environmental determinants of children survival in Bangladesh. Chowdhury et al.¹¹ used multivariate proportional hazards models to find covariates that associated with neonatal and post-neonatal mortality in Bangladesh. Some studies addressed the number of malnourished children.²^–⁵ As no literature is available to the best of our knowledge regarding total number of children"s death among the women of age group 12-49 years in Bangladesh, we attempt to explore the nature of the number of children"s deaths and to identify associated risk factors/ covariates in this study.

A number of regression models for the count response, namely, standard Poisson Regression model, Negative Binomial Regression (NBR) model and Generalized Poisson Regression (GPR) model had been addressed in the literature.³ Applications of these models are based on the assumptions that the mean and variance of the response variable are equal under the standard Poisson model. The GPR model allows flexibility in dealing with over-dispersion or under-dispersion.³ More specifically, an NBR model is suggestive for dealing with over-dispersion.¹⁵

The main objective of the study is to develop a predictive model for the number of child deaths in families in Bangladesh. In this study we applied Negative Binomial Regression (NBR), Zero-Inflated Negative Binomial Regression (ZINBR) and Hurdle Regression (HR) to the count response, number of children"s death, to identify statistically significant predictors/risk factors.

Methods

Study participants

Women aged 12-49 from the Bangladesh Health and Demographic Survey (BDHS) administered in 2011by the National Institute of Population Research and Training (NIPORT), ICF International (USA), and Mitra and Associates. BDHS 2011 is the sixth national demographic and health survey in Bangladesh. The findings of this study can be used for evaluating the Health, Population and Nutrition Sector Development Program (HPNSDP). Sixteen trained interviewing teams administered 17,842 successful interviews of ever-married women aged 12-49. Information was collected from ever-married women of the selected households. The detailed methodology of the survey design, data collection, and data management has been described elsewhere.¹ For this study, we ignore all the missing values and exclude the subjects with missing entries assuming that observations are missing completely at random. Due to some missing observations, finally, we carry out our analysis on data collected from 15,044 married women aged 12-49 years in Bangladesh. The box plot (Figure 1) for the response shows that there is an unusual observation. However, this response value has been kept in the analysis considering its plausibility.

Data management

The response variable, the number of children"s death of ever-married women surveyed, has been derived by adding up total number of son"s death and total number of daughter"s death of a mother. The predictors were assessed by questions regarding age of the respondent (categorized in age groups in years: 13-19, 20-24, 25-29, 30-34, 35-39, 40-44 and 45-49), husband age group in years (13-19, 20-24, 25-29, 30-34, 35-39, 40-44, 45-49, 50+), respondent age at 1^st birth in years (13-19, 20-24, 25-29, 30-39 and 40-49), gap between marriage and 1^st birth in months (0-24, 25-60, 60+), number of family members (<4, 5-7,8-10, 10+), region(seven divisions: Barisal, Chittagong, Dhaka, Khulna, Rajshahi, Rangpur, and Sylhet), place of residence (rural, urban), religion (Islam, others; where "others" includes Hinduism, Buddhism, Christian and unknown religions), respondent"s education (no education, primary school: 1-5 years education, secondary: 6-10 years education, higher: 11+ years education), husband"s education (no education, primary school: 1-5 years education, secondary: 6-10 years education, higher: 11+ years education), does respondent currently work (yes, no), currently residing (living with husband, living elsewhere), incidence of twins (yes, no), has electricity (yes, no), water source (piped, tube-well, and other), toilet facility (standard or not), wealth index was calculated in quintiles (1= poorest and 5 = wealthiest) based on household asset data and access to media (yes or no).

Model justification

Poisson regression model is a natural choice for count response variables. However, in the presence of over-dispersion, Poisson regression model does not perform well in best fitting the data and for prediction. In this study, we test over-dispersion,¹⁵^,¹⁶ where the null hypothesis is that there is no over-dispersion in the data. Hence, the Poisson regression model is the null model against any other alternative model with over-dispersion. Following the notations of Deans and Lawless,¹⁵^,¹⁶ we let Y_i be the response from their subject with covariates X_i.. Then Y_i is distributed as Poisson with mean µi = µ_i(X_i; β), where β is ap-dimensional vector of unknown coefficients. We denote the possible extra-Poisson variation byv

i, in the presence which the standard Poisson model becomes a random or mixed effects Poisson model. Thus, for given X_i and v_i, Y_i~ Poisson (v_i,µ_i), where v_i"s are continuous positive valued random variables that are independent and identically distributed with some finite mean E(v_i) and variance Var(v_i) =τ. If we let E(v_i)= 1, then as Collings and Margolin,¹⁷ Var(Y_i|X_i) = µ

i+ τ µ_i²and the null hypothesis for testing over-dispersion becomes, H₀: τ = 0. Failure to reject the null hypothesis leads to the Poisson regression model. In this study we perform, Dean"s P_B¹⁵ test for over-dispersion using a R packaged DCluster¹⁸^,¹⁹ that generates the test statistic P_B = 13.5292 with p-value <0.000. Rejection of H₀ leads to the application of Negative Binomial type models. Since the variance is greater than the mean and there is about 79% zero counts for the response variable, we apply Zero-Inflated Negative Binomial Regression (ZINBR) and Hurdle Regression (HR) models along with the Negative Binomial Regression (NBR) model to analyze the data.

Data analysis

Simple summary statistics (frequency and percentages) are calculated for the selected socioeconomic and demographic risk factors. Sample mean and sample variance of the response variable are calculated to have an idea of its distribution pattern. Bivariate analysis (based on Pearson Chi-square test) has been performed to examine the association between response variable and each of the selected predictors. To validate the Chi-square test, we categorize the response variable as 0 deaths, 1-2 deaths, and ≥3 deaths. Otherwise the sell frequencies become <5 or zero violating the asymptotic Chi-square assumption. All the significant predictors are then included in the NBR, ZINBR and HR models. For HR model we exclude the predictor age at 1^st birth since inclusion of the variable in the model makes the Hat matrix (X(X/X)^-1>X/) singular. NBR model is better suited to the count response; number of deaths of children to women aged 12-49, due to the presence of over-dispersion. In the case of excessive number of zeros ZINBR and HR perform well in terms modeling number of children"s death. We applied these three models for estimating regression parameters (β) including p-values based on Wald statistics. Finally, we calculated incidence rate ratio (IRR) for all groups of categorical variables. The statistical software package R (Studio) is used for extracting information from BDHS 2011, recoding and model fitting including parameter estimation of the models. We compared the results from NBR, ZINBR and HR models and goodness of fit statistic Akike Information Criteria (AIC).

Figure 1 Box plot for the number of child deaths in a family.

Results and discussion

Sample characteristics

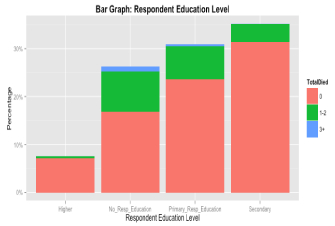
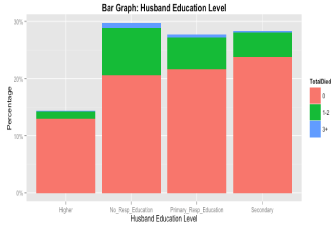
The average age of the surveyed women was 31.44 years while the average age of the husband was 40.97 years. The average age of the women at their first experience of childbirth was 17.89 years. On average a woman gave 2.85 births in their lifetime and the average family size is 5.6.Women gave birth to their first child approximately 3 years after their marriage. About 21% of the women experienced child death and 1.3% women experienced three or more child deaths. 17.47% of women are from the lowest wealth index category and 23.37% are from the highest wealth category. About twenty-six percent of the women had no education. Few of them (7.5%) had 11+ year of education. On the other hand, 29% of the husbands were illiterate but 14% had at least11+ year of education. The majority of the women were Muslims (88.71%). About 66% of the respondents were from urban area. In case of family water sources, 80.52% of families depend on tube-well. About 57% of the families use standard toilets. The percentage of women reported that they had no access to any kind of media is 35%.Box plot (Figure 1) for the number of deaths in a family depicts only one unusual observation. It reveals that one mother experienced 15 child deaths. Figure 2 shows that the distribution of number of children"s death in a family is highly positively skewed. Incidence of more than three child death is almost negligible. Scatter plot in (Figure 3) shows that number of child deaths increases as the respondent"s age increases. The distribution of the number of children"s death with respect to mother"s education (Figure 4) postulates the high incidence of child death for the mothers having no education. Figure 5 also indicates that families with no education of the household head experience more child death. Proportion of deaths for male children and female children are 0.53 and 0.47 respectively. However, the difference of the proportion is not statistically significant (p-value=0. 54).

Figure 2 Histogram for the number of child deaths in a family.

Figure 3 Scatter plot for the number of child deaths in a family vs. respondent age.

Figure 4 Distribution of the number of child deaths in a family with respect to respondent"s (mother"s) education level.

Simple association: Response versus predictor

The associations between the response variable and each of risk factors considered have been examined with Pearson Chi-square at 5% significance level (Table 1) with the following hypothesis H0_i: There is no association between the number of children"s death and their risk factor. Table 2 shows that all the risk factors except respondent"s current work status are significantly associated with the number of deaths of children.

Figure 5 Distribution of the number of child deaths in a family with respect to respondent"s husband education level.

Model fitting

We compare the fitted models with respect to AIC. Although NBR and ZINBR produce very close results, we see ZINBR model acquires the lowest AIC (17,690) among the three fitted models (Table 3). Accordingly, we assert that ZINBR is the best predictive model for the number of deaths of children of women aged 12-49 in Bangladesh and present results from this model. According to the results of ZINBR model (Table 4), one or more of the categories of the predictors (respondent"s age, respondent"s age at 1^st birth, gap between 1^st birth and marriage, number of family members, region, religion, respondent"s education, husband"s education, incidence of twins, source of water, wealth index)are statistically significantly associated with the number of children"s death in a family. The NBR model also suggests almost similar findings [results not shown].On the other hand, HR model[results not shown] shows gap between 1^st birth and marriage, number of household members, region, religion, incidence of twins, and toilet type are significantly related with the response variable. The ZINBR model (Table 4) shows that as the age of mothers increase, they experience higher rate of incidence of child death during their childbearing ages. Mothers having first birth between 20 to 24year"s experiences 35.90% lower child death incidence than the mothers having first birth between 13 to19 years.

	Frequency	Cumulative Frequency	Percentage	Cumulative Percentage
Total Children Died
<2	11880	11880	78.97	78.97
03-May	2923	14803	19.43	98.4
6+	241	15044	1.6	100
Age of Respondent
13-19	1018	1018	6.77	6.77
20-24	2899	3917	19.27	26.04
25-29	3122	7039	20.75	46.79
30-34	2505	9544	16.65	63.44
35-39	2104	11648	13.99	77.43
40-44	1907	13555	12.68	90.1
45-49	1489	15044	9.9	100
Husband Age
15-19	16	16	0.11	0.11
20-24	477	493	3.17	3.28
25-29	1710	2203	11.37	14.64
30-34	2314	4517	15.38	30.03
35-39	2543	7060	16.9	46.93
40-44	2256	9316	15	61.93
45-49	2073	11389	13.78	75.7
50+	3655	15044	24.3	100
Age at 1^st Birth
13-19	11343	11343	75.4	75.4
20-24	3024	14367	20.1	95.5
25-29	556	14923	3.7	99.2
30-39	119	15042	0.79	99.99
40-49	2	15044	0.01	100
	Frequency	Cumulative Frequency	Percentage	Cumulative Percentage
Gap Between Marriage and 1st Birth
<24 Months	8360	8360	55.57	55.57
25-60 Months	5238	13598	34.82	90.39
60+ Months	1446	15044	9.61	100
Household Members
< 4	5729	5729	38.08	38.08
05-Jul	751	6480	4.99	43.07
08-Oct	6732	13212	44.75	87.82
8+	1832	15044	12.18	100
Region
Barisal	1768	1768	11.75	11.75
Chittagong	2440	4208	16.22	27.97
Dhaka	2533	6741	16.84	44.81
Khulna	2225	8966	14.79	59.6
Rajshahi	2236	11202	14.86	74.46
Rangpur	2122	13324	14.11	88.57
Sylhet	1720	15044	11.43	100
Residence
Rural	5153	5153	34.25	34.25
Urban	9891	15044	65.75	100
Religion
Islam	13345	13345	88.71	88.71
Other	1699	15044	11.29	100
Respondent's Education
No Education	1138	1138	7.56	7.56
Primary	3960	5098	26.32	33.89
Secondary	4656	9754	30.95	64.84
Higher	5290	15044	35.16	100

	Frequency	Cumulative Frequency	Percentage	Cumulative Percentage
Husband Education
No Education	2157	2157	14.34	14.34
Primary	4474	6631	29.74	44.08
Secondary	4159	10790	27.65	71.72
Higher	4254	15044	28.28	100
Is Respondent Currently working?
No	13264	13264	88.17	88.17
Yes	1780	15044	11.83	100
Husband’s Working Status
Businessman	3645	3645	24.23	24.23
Labor Intensive	10292	13937	68.41	92.64
Service/Professional	1107	15044	7.36	100
Respondent Currently Residing with
Living Elsewhere	1646	1646	10.94	10.94
Living with Husband	13398	15044	89.06	100
Have any Twin
No	14686	14686	97.62	97.62
Yes	358	15044	2.38	100
Electricity
No	6097	6097	40.53	40.53
Yes	8947	15044	59.47	100
Water Source
Others	1323	1323	8.79	8.79
Piped Water	1607	2930	10.68	19.48
Tube-well Water	12114	15044	80.52	100
Type of Toilet
Not Standard	6488	6488	43.13	43.13
Standard	8556	15044	56.87	100
	Frequency	Cumulative Frequency	Percentage	Cumulative Percentage
Wealth Index
Lowest	2628	2628	17.47	17.47
Second	2826	5454	18.78	36.25
Third	2918	8372	19.4	55.65
Fourth	3156	11528	20.98	76.63
Highest	3516	15044	23.37	100
Media Access
Access	9837	9837	65.39	65.39
No Access	5207	15044	34.61	100

Table 1 Prevalence of the number of child deaths with predictors, BDHS, 2011

Among the divisions, all but Dhaka is significantly associated with the number of children"s death (Barisal division is a reference category). The incidence rate ratio of children"s death in Sylhet is 1.303 times higher than that of Barisal. Conversely, mothers living in Khulna experience 0.328 times lower death incidence than the mothers living in Barisal. Mothers having no education experience 2.06 times higher incidence of death than that of mothers having more than 11 years education. The results (Table 4) also show that the women having twin births are subject to 3.53 time"s higher child death incidence. The mothers who have availability of tube-well and piped water possess lower rate of child death incidence than those of who do not have the facility. Deriving a predictive model for the number of children"s death of women is in general a hard task. Numerous factors must be taken into account. It is not always feasible to consider these issues in modeling the number of children"s death. Thus the results should be interpreted with caution.

Conclusion

Our study suggests that ZINBR is the right model to identify the risk factors of the number of children"s death in families in Bangladesh. Respondent"s age, respondent"s age at 1^st birth, gap between 1^st birth and marriage, number of family members, region, religion, respondent"s education, husband"s education, incidence of twins, source of water, wealth index are statistically significantly associated with the number of children"s death in a family. The number of children"s death affects about 28% of all ever-married women aged 12–49 years in Bangladesh, and it indicates a poor health system. A number of strategies are reported in studies for the reduction of child mortality.⁵^,⁶ From this study, we identify some of the well-established demographic and socioeconomic risk factors for the number of children"s death to women aged 12-49 in Bangladesh. Among these the most important one, in our opinion, is the education of a mother. Increase in the number of years of education for women delays the age at marriage, age at first birth and perhaps gap between successive births, all of which are identified as significant predictors for the number of children"s death in the current study. Education of a mother is also strongly correlated with nutrition status of the family. Intervention for improving the nutrition status is important since malnutrition is one of the major causes of child mortality in Bangladesh.³

	Chi Square	df	p-value
Respondent Age	1524.181	12	0.00000
Husband Age	1282.327	14	0.00000
Respondent Age at 1st Birth	111.307	8	0.00000
Gap between Marriage and 1st Birth	14.24685	4	0.00655
Number of Members in the Family	19.21245	6	0.00382
Region	65.18007	12	0.00000
Residence	67.39046	2	0.00000
Religion	18.33311	2	0.00010
Respondent Education	1117.853	6	0.00000
Husband Education	526.0294	6	0.00000
Is Respondent Currently Working	1.158246	2	0.56039
Husband Occupation	66.90243	4	0.00000
With Whom Respondent Currently Living	43.05137	2	0.00000
Any Incidence of Twins in the Family	564.2712	2	0.00000
Having Electricity	121.0506	2	0.00000
Source of Water	78.77498	4	0.00000
Type of Toilet	68.68566	2	0.00000
Wealth Index	283.5333	8	0.00000
Access to Media	314.0064	2	0.00000

Table 2 The association between number of child deaths and predictors, BDHS, 2011

	AIC	Log-Likelihood
NBR	17756.00	-8825.992
ZINBR	17690.00	-8826
Hurdle	20118.00	-10040.00

Table 3 Model Comparison

	Coeff	SE	Wald		P-Val	RR
(Intercept)	-3.040	1.028	-2.957		0.003	0.048
Respondent Age (Year)
20-24	0.375	0.145	2.584		0.010	1.455
25-29	0.743	0.154	4.835		0.000	2.103
30-34	1.264	0.161	7.844		0.000	3.539
35-39	1.470	0.166	8.857		0.000	4.349
40-44	1.845	0.169	10.951		0.000	6.330
45-49	2.152	0.171	12.598		0.000	8.599
Husband Age (Year)
20-24	0.052	1.027	0.050		0.960	1.053
25-29	-0.052	1.021	-0.050		0.960	0.950
30-34	0.076	1.022	0.075		0.940	1.079
35-39	0.058	1.023	0.057		0.954	1.060
40-44	-0.041	1.024	-0.040		0.968	0.960
45-49	0.060	1.024	0.059		0.953	1.062
50+	0.174	1.025	0.170		0.865	1.190
Respondent Age at 1st Birth (Year)
20-24	-0.444	0.053	-8.421		0.000	0.641
25-29	-0.633	0.116	-5.458		0.000	0.531
30-39	-1.155	0.283	-4.080		0.000	0.315
40-49	-10.946	201.965	-0.054		0.957	0.000
The time interval between marriage and 1st month(Birth)
25-60	-0.149	0.037	-3.986		0.000	0.862
60+	-0.035	0.063	-0.547		0.584	0.966
Number of Members in the Family
5-7	-0.095	0.038	-2.506		0.012	0.910
8-10	-0.266	0.059	-4.484		0.000	0.766
10+	-0.126	0.089	-1.411		0.158	0.881
	Coeff	SE	Wald		P-Val	RR
Region (Division)
Chittagong	0.066	0.064	1.035	0.301		1.069
Dhaka	-0.061	0.065	-0.940	0.347		0.941
Khulna	-0.397	0.068	-5.821	0.000		0.672
Rajshahi	-0.232	0.066	-3.488	0.000		0.793
Rangpur	-0.194	0.066	-2.920	0.003		0.824
Sylhet	0.264	0.067	3.921	0.000		1.303
Residence
Urban	-0.016	0.044	-0.359	0.719		0.984
Religion
Others	-0.226	0.060	-3.798	0.000		0.798
Respondent educational status
No Education	0.723	0.146	4.952	0.000		2.060
Primary	0.596	0.143	4.176	0.000		1.814
Secondary	0.228	0.137	1.661	0.097		1.256
Husband Educational Status
No Education	0.452	0.098	4.607	0.000		1.572
Primary	0.383	0.096	4.003	0.000		1.466
Secondary	0.251	0.091	2.745	0.006		1.285
Is Respondent Currently Working
Yes	0.006	0.054	0.119	0.906		1.006
Husband Occupational Status
Labor	-0.075	0.042	-1.779	0.075	0.928
Professional	0.046	0.097	0.475	0.634	1.047
Respondent Currently Living with
Husband	0.116	0.065	1.788	0.074	1.123
Incidence of Twin
Yes	1.263	0.064	19.604	0	3.536
Having Electricity
Yes	-0.083	0.049	-1.703	0.089	0.921
Source of Water
Piped water	-0.192	0.101	-1.907	0.056	0.825
Tube-well	-0.096	0.071	-1.356	0.175	0.908
Toilet Type
Standard	-0.067	0.039	-1.721	0.085	0.935
Wealth Index
Poorest	0.008	0.051	0.156	0.876	1.008
3rd Group	-0.074	0.055	-1.342	0.18	0.929
4th Group	-0.13	0.064	-2.039	0.041	0.878
Wealthiest	-0.323	0.081	-3.971	0	0.724
Access to Media
No	0.057	0.041	1.406	0.16	1.059

Table 4 Results of multivariate Zero-Inflated Negative Binomial (ZINBR) and Negative Binomial regression (NBR) and Hurdle Model (HR) to study the total number of deaths of children in Bangladesh

Increasing parental educational facilities can improve child nutrition and child mortality as well. Facilities to safe drinking water and safe sanitation contribute much to reduce malnutrition. However, due to unavailability of malnutrition data on children this study could not address how malnutrition would contribute to the number of children"s death. The findings of this study on the socio-demographic risk factors /determinants of the number of children"s death to women aged 12-49 will provide the policymakers proper insight and guidance toward implementation of the needed intervention to reduce child mortality in Bangladesh and in other countries around the world. Reducing child mortality through intervening its significant determinants will insure the sustainability of the MDG 4 achievement program in Bangladesh. As mentioned earlier, child death depends on a diverse number of factors including socio-demographic and physiological factors in a complex pattern. The current study explores the role of socio-demographic factors in predicting the number of children"s death in women aged 12-49 in Bangladesh. More extensive studies focusing on the interplay between socio-demographic factors and other relevant factors on the child death should be carried out in order to fully understand the risk factors of child mortality.