Advances in
eISSN: 2572-8490


Research Article Volume 4 Issue 2
Department of Physics, Qassim University, Saudi Arabia
Correspondence: Musa Saad HE, Department of Physics, College of Science, Qassim University, Buraidah 51452, Saudi Arabia, Tel +966509353808, Fax +966163800911
Received: November 09, 2017 | Published: March 15, 2018
Citation: Musa SHE. Half-metallic double perovskites Sr2CrWO6 and Sr2FeReO6 materials for spintronics applications. Adv Tissue Eng Regen Med Open Access. 2018;4(2):28–33. DOI: 10.15406/atroa.2018.04.00073
Double perovskite-like materials which include magnetic transition elements have relevance due to the technological perspectives in the spintronics engineering. In this study, we report the studies of the electronic and magnetic properties of Sr2CrWO6 and Sr2FeReO6 as spintronics materials at room temperature by using the linear muffin- tin orbitals (LMTO) method through the atomic-sphere approximation (ASA) within the local spin density approximation (LSDA). The interchange-correlation potential was included through the (LSDA+U) method. The band structure results at room-temperature predict half-metallic ferrimagnetic ground state for Sr2CrWO6 and Sr2FeReO6 with total magnetic moment of 1.8780μB and 3.1841μB per formula unit, respectively, agreement with the previous theoretical and experimental results.
Keywords: spintronics, double perovskites, half-metallic, LMTO-ASA, LSDA+U method
Spintronics, analogous to the electronics science and engineering, is a complex term means spin-transport electronics, also named magneto-electronics. Spintronics is an emerging technology in solid-state devices,1‒3 exploits both the intrinsic spin of the electron and its associated magnetic moment, in addition to its fundamental electronic charge, i.e. Spin (S=±½)+Charge (e-)=Spintronics. Spintronics came into view from the observations: (i) spin-polarized electron injection from a ferromagnetic (FM) metal to a normal metal,4 (ii) giant magnetoresistance (GMR) phenomenon in Fe/Cr super-lattice and in Fe–Cr–Fe trialed,5,6 and (iii) magnetic tunnel junctions (MTJ).7,8 Materials with high spin-polarization (P), preferably 100%, are promising as materials for spintronics devices and thus have been searched enthusiastically. The ratio of spin-polarization (P) can be defined by means of the spin-up and spin-down density of states (D↑, D↓) around the Fermi level (EF), as:
(1)
This is extremely interesting as a promising candidate of a spin injector in spintronics. The material with perfect spin-polarization is characterized as a half-metal (HM); HM materials are good candidates because they can have high spin polarization, P=±1 (P=100%), at high temperature.
The thin insulator sandwiched between two FM contacts (FM/I/FM) generates tunnel current due to quantum effect by using small voltage; insulating layer provides quantum mechanical tunnelling of electrons from one ferromagnetic layer to another.8 Consequently, the electrical resistance will be low when the magnetizations of two FM layers are parallel (FM↑/I/FM↑) or (FM↓/I/FM↓). On the other hand, resistance (R) rises for antiparallel magnetization of the FM layers, (FM↑/I/FM↓) or (FM↓/I/FM↑). This phenomenon is known as tunnelling magneto resistance (TMR) effect.7 The low-field GMR in granular materials is dominated by the inter-grain spin-dependent TMR through insulating grain boundaries, reflecting the spin-polarization of the ferromagnetic grains.7 Of course, TMR is favorited by the alignment of the magnetization of the neighboring grains under application of the magnetic field. Based on the resistivity of the material, the magneto resistance (MR) can be defined as7
(2)
Where, and are the resistivity with (H>0) and without (H=0) applied magnetic field, respectively. Therefore, the MR phenomenon is being the field-dependent resistance (R) as a function of the applied magnetic field. However, TMR is a pure interface effect and does not require spin transportation in insulator layer. The corresponding TMR in an FM1/I/FM2 magnetic tunnel junction (MTJ) can be described by the relative fraction:
(3)
Where, the resistances R are labeled by the relative orientations of the magnetization in FM1 and FM2, and it is possible to change the relative orientations between ↑↑ and ↓↓, even at small-applied magnetic fields. Using Julliere model which assumes constant tunneling matrix elements and those electrons without spin flip-flop,7,8 Equations. (1) and (3) yield:
(4)
Double perovskites have the chemical formula A2BB'O6 crystallize in the rock-salt (NaCl) structure with alternate perovskite units ABO3 and AB'O3 along three crystallographical axes.9 The corner of each perovskite unit cell are in turn occupied by different transition-metal atoms B and B' with oxygen atoms located in between forming alternate BO6 and B'O6 octahedra.9,10 The large alkaline-earth metal atoms A2+ occupied the body-centered site with 12-fold oxygen coordination in each unit cell.11 In the ionic model of alkaline-earth metal based double perovskites, the pair of transition-metal ions are in the 8+ valence state, (BB')8+. The interaction between two magnetic ions B and B' in double perovskites A2BB'O6 controls by the long-range super exchange (–B–O–B'–) instead of double-exchange (–B–O–B–) in perovskite ABO3.12,13
Materials with high spin-polarization of the charge carriers, the current, have attracted a great deal of attention owing to their technological applications in spintronics,14 magnetotransport devices as well as their rich and challenging physical properties.9‒14 In particular, an ideal material with 100% spin-polarization is called a half-metal.15 Such materials can be found in several materials classes; in classic inorganic oxides, such as magnetite (Fe3O4)16 and chromium dioxide (CrO2),17 in manganite perovskites as in (LaMnO3)18 and in Heusler alloy compounds as in (Co2Cr1-xFexAl),19,20 as well as in the group of double perovskites.9,12,13 Double perovskites are of special attention, since within this group half-metals with above room-temperature (RT) are found, such as in (Ca2FeMoO6), (Sr2FeMoO6), (Ba2FeMoO6),21,22 and in (Sr2CrMoO6).21,22 The ordered double perovskites, such as (Sr2FeMoO6), (Sr2FeReO6), (Sr2CrWO6), etc., are among the very few materials that allow electrons of one spin direction to move through them as though they were passing through a normal metal, while blocking electrons of the opposite spin. Materials that behave this way at RT are even more exotic, so their conduction bands have a fully spin-polarization.9 (Sr2FeReO6), (Sr2CrWO6) double perovskites, in particular, have attracted more attention due to their fairly high transition temperature from a paramagnetic (PM) to ferromagnetic (FI) state, which makes them and their related compounds candidates for future spintronics applications.
The first-principles linear muffin-tin orbital (LMTO) method with atomic-sphere approximation (ASA) has been employed to perform self-consistent band structure calculations within the local spin density approximation (LSDA). In LMTO-ASA, which is similar to the multiple-scattering Korringa-Kohn-Rostoker (KKR) method,24 the potential is approximated by a muffin tin potential, i.e., it is spherically symmetric around the atomic sites and constant in the interstitial volume. Moreover, ASA takes the one-electron potential and charge density to be spherically symmetric inside space-filling Wigner-Seitz (WS) spheres whose overlap is neglected, the interstitial volume, now integrating to zero.24 The von Barth–Hedin parameterization for exchange-correlation potential is used in the calculations.9,25 The Hartree potential is expanded in term of spherical harmonic up to 6, therefore, Sr (5s 4p 4d), Cr/Fe (4s 4p 3d), Mo (5s 5p 4d), W (6s 6p 5d) and O (2s 2p) LMTOs were input as valance states, while Sr (4s), Cr/Fe (3p), Mo (4s 4p), W (5p 4f) fixed as semicore states in the unit cells. It has been established that the structures are close enough, that no empty sphere (ES) is needed to introduce in the unit cells.17 The numbers of divisions along reciprocal lattice vector which will set up the mesh for integrating valence state are selected as 6×6×6. Special k points of 120 in the irreducible Brillouin zone (IBZ) was used in band structure and density of states calculations. A single kappa LMTOs basis set expanded in spherical harmonic up to the angular momentum lmax=6, was used for the valence-band charge densities and potential inside the non-overlapping muffin-tin spheres.24 The interchange-correlation potential was included through the LSDA+U method, where the on-site Coulomb energy (U) has been in used. The correlation parameters, Coulomb energy (U) and Hund's rule exchange (J), were utilized for strongly correlated 3d and weakly 5d electrons in the calculations. The Hubbard parameters (U=4 eV, J=0.98 eV) are used for Cr/Fe (3d) states,9,25 even as ( U=1 eV, J=0.96 eV) are used for W/Re (5d) states.1,17 The resolving of spin up and down in total and partial densities of states for Sr2CrWO6 and Sr2FeReO6 were calculated and obtained from the LSDA+U calculations.
Crystal structures
In the present study we report systematic studies on the Cr/Fe (3d) and W/Re (5d) orbitals contributions to the electronic and magnetic structures of two close relative members of strontium double perovskites, Sr2CrWO6 and Sr2FeReO6. Where, W and Re are neighboring 5d transition-metal elements in periodic table with the ordinary electronic configurations of [Xe] 6s24f145dn, where n=4 for W (Z=74) or n=5 for Re (Z=75), [Xe] denotes the configurations of the noble gas Xenon core. For chromium and iron Cr/Fe, Cr has an odd electron configuration of [Ar] 4s13d5 owing to the lower energy of the high spin configuration, not [Ar] 4s23d4 as it might expect, where a half-filled d sublevel is more energetically favorable than a half-filled s sublevel, so one of the 4s electrons is promoted to a 3d orbital. On the other hand, iron (Fe) has ordinary electron configuration of [Ar] 4s23d5. Cr and Fe exhibit a wide range of possible oxidation states, where the +3 state is most stable energetically.25‒27 Accordingly, the valence configurations of transition-metal ions in Sr2CrWO6 are; Cr3+ (3d3) and W5+(5d1) in high spin state with valence spin magnetic moments of S=3/2 and S=1/2 according to the Hund's rule, respectively. Consequently, the theoretical total magnetic moment is 2 μB per formula unit cell for the ferrimagnetic ground state. In other compound, Sr2FeReO6, where the ion Fe3+ (3d5) is in high spin state of S=5/2, ion Re5+(5d2) is highly ionized with valence spin magnetic moment of S=1. As a result, the total magnetic moment for the ferrimagnetic ground state is 3 μB per Sr2FeReO6.
For cubic Sr2CrWO6 and Sr2FeReO6 perovskites with space group Fm-3m (No. 225), we used the experimental lattice constants of a=7.890Å from28 and a=7.832Å from,9 respectively, closed to the theoretical values calculated using SPuDS27 7.8587Å and 7.8858Å, correspondingly, see Table 1. The magnetic structure in double perovskites can be assign to the AFM superexchange interactions between two very different transition magnetic ions, 9,25 such as Cr/Fe (3d) and W/Re (5d) in this study, via intermediated O2-(2p) ions (Cr/Fe –O– W/Re). In addition to, the naturally small magnetic moment at W/Re (5d), is believed to be not intrinsic, but is induced by the strong magnetic ions Cr/Fe(3d) (Table 2).
Structural parameter |
Sr2CrWO6 |
Sr2FeReO6 |
|
Space group |
Fm-3m (No. 225) |
Fm-3m (No. 225) |
|
Lattice constants a = b = c (Å) |
7.8587 |
7.8858 |
|
Unit cell volume V (Å3/u.c.) |
485.189 |
490.394 |
|
Tolerance factor t |
1.001 |
0.9974 |
|
Oxygen coordinate O (u,0,0) |
0.252 |
0.2556 |
|
Bond length
|
Sr– O(Å) |
2.7782 |
2.7884 |
Cr/ Fe–O(Å) |
1.9805 |
2.0155 |
|
W/ Re–O(Å) |
1.9485 |
1.9275 |
|
Table 1 Crystal structure parameters of double perovskites Sr2CrWO6 and Sr2FeReO6
Atom |
Multiplicity |
Wyckoff |
x |
y |
z |
Sr |
8 |
c |
¼ |
¼ |
¼ |
Cr/Fe |
4 |
a |
0 |
0 |
0 |
W/Re |
4 |
b |
½ |
½ |
½ |
O |
24 |
e |
u |
0 |
0 |
Table 2 Atoms, multiplicities, Wyckoffs and positions (x,y,z) for the cubic (Fm-3m; No. 225) double perovskites Sr2CrWO6 and Sr2FeReO6
Electronic and magnetic structures
Figure 1 illustrates the total densities of states (TDOSs) of Sr2CrWO6 and Sr2FeReO6 from band structure LSDA+U calculations. In spin-up TDOSs, there are energy gap of about 1.33 eV in Sr2CrWO6 and 2.18 eV in Sr2FeReO6 between the occupied Cr/Fe (3d) and unoccupied W/Re (5d) partial bands. Since the energy gap in the spin-up produces from the antiferromagnetic coupling between Cr/Fe (3d) and W/Re (5d) states, as shown in Figure 2, this situation emerge as peaks of 3d and 5d bands polarized antiferromagnetically demonstrate the Cr/Fe (3d) ↑ and W/Re (5d)↓ form. Therefore, the spin-up electrons are insulating while the spin-down electrons are metallic, resulting in full (100%) spin-polarized of the conduction electrons at EF. For that reason, Sr2CrWO6 and Sr2FeReO6 materials allow electrons of spin-down direction to move through them as though they were passing through a normal metal, while blocking electrons of the spin-up. The obtained results of Sr2CrWO6 and Sr2FeReO6 are agreement with previous LSDA+U calculations.9,25,29 As seen in Figure 2, the conduction bands in spin-down orientation is attributed mainly to the contributions of W (5d) and Re (5d) ions with tiny contributions of Cr (3d) and Fe (3d), correspondingly. Compare TDOSs with PDOSs, the level distributions in of Sr2CrWO6 and Sr2FeReO6 are overall very similar, except a peak between 1 eV and 3 eV, above EF, is higher in Sr2FeReO6 than in Sr2CrWO6. This dissimilarity, as seen in Figure 2, due to the extra electron in Re (5d2) than in W (5d1).
In order to understand in some more detail the origin of the electronic and magnetic characters of Sr2CrWO6 and Sr2FeReO6, we critically examine the partial electronic density of states (PDOS) of these systems. The basic critical ingredients in the TDOS are the d states of the Cr/Fe and W/Re atoms, which in turn are split into t2g and eg states by the octahedral crystal field (OCF) produced by the oxygen octahedra. The t2g states having lower energy and place for three electrons per spin channel, whereas the eg states are higher in energy and have place for two electrons per spin channel. Furthermore, due to the exchange splitting, t2g bands degenerate into double orbitals (dxz and dyz) and one singlet orbital (dxy), while eg bands degenerate into two singlet orbitals (dx2 –y2 and dz2), as seen in Figure 3, which show the partial densities of states of t2g, eg and 2p orbitals in Sr2CrWO6 and Sr2FeReO6.
From the PDOS in Figure 3A, the three-fold degenerate Cr t2g states of the spin-up channel are filled Cr3+ (3d3:t2g3↑); consequently the dxy↑, dxz↑ and dyz↑ orbitals are at the energy range, about -7 eV~-1.5 eV in the valance bands. Therefore, the EF ends up in the CF gap of ∆o≈1.5 eV between Cr t2g and eg states. A similar situation is observed in the half-metallic close-relative Sr2FeReO6.29,30 Due to the antiferromagnetic coupling in Cr (3d) –W (5d), it is the spin-down channel in W (5d) which is the occupied one, and it contains one electron in t2g states W5+ (5d1:t2g1↓). This means that the W (5d) t2g spin-down states are only filled to about one-two, resulting in high density of states of dxy and dyz at the EF in spin-down channel. In addition to, due to hybridization between states in Sr2CrWO6, Cr t2g↓ states achieved small occupation, while W (5d) states in the spin-up channel are essentially empty; hybridization with Cr t2g↑ states results nevertheless in a finite, small occupation above EF.
On the other hand, from the PDOS in Figure 3B, the Fe t2g and eg states are full-filled in the spin-up orientation; Fe3+ (3d5: t2g3↑ eg2↑) in the high spin state; the electronic configuration can be set of orbitals as (dxy↑)1, (dxz↑ and dyz↑)2, (dx2–y2)1 and (dz2)1 extend from -8.0 eV to -2.0 eV in the valance bands. The exchange splitting is about 7.5 eV, larger than the CF splitting, ∆o ≈ 2.25 eV, resulting in the high-spin of Fe (3d) states. At the same time, spin-down channel in Re (5d) which is the occupied one, and it contains two electron in t2g states Re5+(5d2: t2g2↓). Therefore, the Re t2g spin-down states are only filled to about two-three, emerged as a high spin-down DOS of dxy and dyz at EF. Inversely, neither Fe t2g ↓ nor Re (5d) ↑ states have contribution to the bands around EF, while the O(2p) bands are at a much lower energy from -9 to -2 eV.
Finally, the magnetic structure in Sr2CrWO6 and Sr2FeReO6 double perovskites can be assign to the antiferromagnetic superexchange interactions between Cr/Fe(3d) and W/Re(5d) via intermediated oxygen atoms in the 180o long-chain Cr (3d-t2g↑)–O(2pπ)–W(5d-t2g↓) and Fe (3d-t2g↑)–O (2pπ) – Re (5d-t2g↓), correspondingly. The calculated spin magnetic moments from LSDA+U for Sr2CrWO6 are; 2.9188μB / Cr, -1.0435μB / W with a total magnetic moment of 1.8780μB, which is 94% agreement to the later LSDA+U result, 2.01μB.27,29 For Sr2FeReO6, 4.5778μB for Fe, -1.3438μB for Re, and the total magnetic moment found to be 3.1841μB, also agreement to the LSDA+U result, 3.06μB.9 The bands scheme for both compounds are illustrated in Figure 4, the results can be to resume by means the simple model describes the effect of filling t2g and eg orbitals in 3d and 5d bands for spin-up and -down configurations.
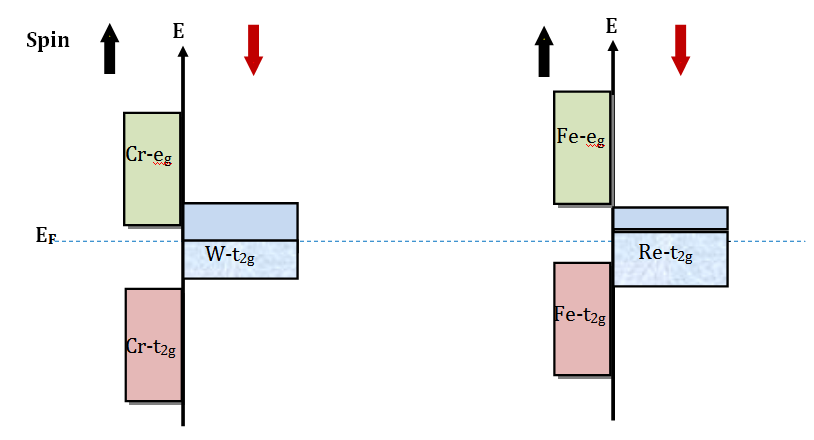
Figure 4 Representation of the electronic density of spin-up and spin-down states in 100% electronic spin-polarization half-metallic in Sr2CrWO6 and Sr2FeReO6. The quantity of filling signifies the effect of t2g and eg orbitals in 3d and 5d bands per unit volume and per unit energy; E. EF is the Fermi energy.
We have comparatively studied the electronic and magnetic characterizations of double perovskites Sr2CrWO6 and Sr2FeReO6 by using the linear muffin- tin orbitals through the atomic-sphere approximation method within the local spin density approximation, including the interchange-correlation potential through the LSDA+U method. The band structure results demonstrated half-metallic ferrimagnetic ground state for Sr2CrWO6 and Sr2FeReO6 with total magnetic moment of 1.8780μB and 3.1841μB per formula unit, respectively, in exact agreement with the theoretical and experimental results. The obtained HM-FiM feature in double perovskites Sr2CrWO6 and Sr2FeReO6 makes these materials suitable for many applications. It established that they have a high degree of electronic spin polarization which means that they will have potential spin transport electronics (spintronics), where spin currents are utilized as well as charge currents.
None.
The authors declare no conflict of interest.

©2018 Musa. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.