We present a three-dimensional (3D) lattice model based on the differential adhesion hypothesis (DAH) to study self-assembly and fusion of multicellular aggregates, which forms the foundation for the scaffold-less biofabrication of tissues and organs, known as “bio-printing”. In this new technology, live multicellular aggregates are used as bio-ink to make tissue or organ constructs via the layer-by-layer deposition technique in biocompatible hydrogels; the printed bio-constructs embedded in the hydrogels are then placed in bioreactors to undergo the fusion process to form the desired functional tissue or organ products. Our in-silico approach is an agent-based method, which uses the kinetic Monte Carlo (KMC) algorithm to evolve the cellular system on a 3D lattice. In this model, the cells and the hydrogel media, in which cells are embedded, are coarse-grained to material’s points on the lattice, where the cell-cell and cell-medium interaction are quantified by adhesion and cohesion energies. In a multicellular aggregate system with a fixed number of cells and fixed amount of hydrogel media, the effect of cell differentiation, proliferation, and death are tactically neglected in the current model, which can be readily included in the model, and the interaction s primarily dictated by the interfacial energy between cell and cell as well as between cells and medium particles on the lattice, respectively. The KMC method is applicable to transient simulations of fusion of multicellular aggregates at the time and length scale appropriate to biofabrication. Numerical experiments are presented to demonstrate fusion and cell sorting during tissue and organ maturation processes.

Keywords: Biofabrication; Bioprinting; Multicellular aggregates; Cellular aggregate fusion; Kinetic monte carlo; Differential adhesion hypothesis

Recently a novel biomimetic fabrication technology, called “bioprinting” has emerged in tissue engineering. This technology is operationally defined as computer-aided, layer-by-layer deposition of biologically relevant material with the purpose of engineering functional 3D tissues and organs.^1-11 Challenges in this technology lie in both innovation in engineering and new discovery and understanding in biological science, chemistry and physics. Issues in biology and chemistry are related to identifying cell sources and optimizing hydrogels for cell delivery, growth and differentiation; issues in engineering are focused on innovation in designing biofabrication processes for printing of functional tissues and preparation, transport or delivery of the multicellular aggregates; issues in modeling lie in developing faithful mathematical and physical models and in- silico predicative tools to understand and simulate mechanisms underlying the biofabrication process and thereby to facilitate biological and engineering design.

In the bioprinting technology, prefabricated multicellular aggregates are used as fundamental building blocks to construct the 3D tissue or organ. The aggregates (the bio-ink) are first prepared in the form of tissue spheroids or other stable geometrical forms that consist of cells blended with biocompatible hydrogels. They are then directly deposited by computer-aided design tools into desired 3D tissue or organ constructs via the layer-by-layer deposition technique. The printed bioconstruct immersed in a hydrogel matrix is then placed in bioreactors for further maturation, during which the aggregates undergo a fusion process to form the desired functional tissue or organ products by following the natural rule of histogenesis and organogenesis.

Mathematical modeling of self-assembly of cells and cellular aggregate fusion process can help one to understand the origin of intercellular forces due to cellular responses in cells as well as tissue fusion and quantitatively characterize the mechanochemical process during tissue morphogenesis, accurately predict and optimize post printing structure formation, and intelligently develop approaches in drug design and tissue engineering. Developing models and computational tools to simulate the processes is a challenging and very promising new area where only a few studies have been done by far.

The popular theoretical and computational models of multicellular systems that describe cellular self-assembly processes and tissue fusion in specific problems can be divided roughly into two classes:

1. Continuum models described by densities of cells and regulatory proteins;
2. Individual cell-based (or agent-based discrete) models in which each cell is treated as a separate agent interacting with neighboring cells or particles.

In continuum models, cellular aggregates are represented in densities (or concentrations) of identical cells whose properties, such as cellular proliferation or death, movement speed and direction, are characterized by the averages for the whole cell assembly. These models are by definition deterministic and can include several cell phenotypes for different cellular aggregates. The continuum models can be used to model dynamics of tissues with reasonably large size. They can provide a global view of cell self-assembly and cellular aggregate fusion, and show the potential to match some image-based experimental data. Their simplicity sometimes can allow analytical investigation to capture key underlying mechanisms. Examples of continuum models can be found in.^12-21

However, when we consider structures or behavior which occur at the scale of single cells, continuum approaches are not accurate enough to give even qualitatively correct results. In this situation, we need to use the individual cell-based models that preserve the identity and behavior of single cells. Moreover, these models can integrate measurements from different in vitro experiments, reconstruct certain aspects of in vivo environments and allow for a systematic analysis of the influence of individual cells as well as combined factors on overall tissue dynamics. Examples of these models can be found in.^22-39 In the agent based approach, we design fundamental rules for neighboring agents (cells in the context of aggregates) to interact with neighboring cells or particles. These probabilistic rules coupled with the fluctuation dynamics can lead to the desired collective or mesoscopic dynamics.

A 3D Lattice Model Based on DAH and Time Evolution via Kinetic Monte Carlo Methods

In,^40,41 we developed a 3D multicellular lattice model which describes the mechanical interactions between cells as well as between cells and media based on the differential adhesion hypothesis (DAH).⁴² DAH implies that early morphogenesis is a self-assembly process, whereby mobile and interacting cells spontaneously give rise to the morphological structure. This hypothesis states that

1. Cell adhesion in multicellular systems depends on energy differences between different types of cells and
2. An aggregate of cells are motile enough to reach the configuration which minimizes the interfacial energy of the system.

In light of DAH, embryonic tissues mimic the behavior of highly viscous, incompressible liquids in the time scale of tissue formation.DAH has guided in vitro studies of cell self-assembly and cellular aggregate fusion.^40,41

Here we model the multicellular system on a 3D cubic lattice and treat cells as point particles on the lattice sites. We associate each site $\overrightarrow{r}=\left(x,y,z\right)$ of the lattice with an integer index ${\sigma }_{\overrightarrow{r}}$ (also called a spin), which accounts for the occupancy of the site by a cell ${\sigma }_{\overrightarrow{r}}\ne 0$ or a similar-sized volume element of hydrogel medium ${\sigma }_{\overrightarrow{r}}=0$ . The total pair interaction energy of the system is given by $E={\displaystyle {\sum }_{\langle \overrightarrow{r},\overrightarrow{r}\text{'}\rangle }J\left({\sigma }_{\overrightarrow{r}},{\sigma }_{\overrightarrow{r}\text{'}}\right)}$ , where $\overrightarrow{r}$ and $\overrightarrow{r}\text{'}$ label lattice neighboring sites and the sum runs over first, second, and third nearest neighbors. The term $J\left({\sigma }_{\overrightarrow{r}},{\sigma }_{\overrightarrow{r}\text{'}}\right)=-E_{ij}$ is the contact interaction energy between two particles of type $i$ and type $j$ , and $E_{ij}$ can take positive quantities $E_{mm}$ , $E_{cc}$ , $E_{cm}$ , which account for the interaction strengths between medium-medium, cell-cell, and cell-medium pairs, respectively.⁴³ The conformational evolution of the multicellular system is energetically driven to the configuration which minimizes the free energy of the system.

We apply the kinetic Monte Carlo (KMC) method⁴⁴ to the 3D lattice model to evolve the multicellular system. The dynamics of cells depends on the transition rates of swapping cells with adjacent cells of different type and/or with medium particles. The swap is taken with its rate defined by the Arrhenius relation $r=W_0\exp \left(-\Delta E/E_T\right)$ where $W_0=1/{\tau }_0$ corresponds to the cell swapping frequency with ${\tau }_0$ the characteristic or relaxation time unit, E is the effective energy, and $E_T$ is the characteristic energy scale of biological fluctuations.⁴⁰ The change of energy due to the swap, $\Delta E$ , is assumed to depend only on the local environment of the swapping cells/particles. One advantage of the KMC method is that it can provide the transition rates which are associated with possible configurational changes of the multicellular system, and then the corresponding time evolution of the system can be expressed in terms of these rates.

In,⁴⁰ we calibrated the model parameters in the KMC code by simulating fusion of two spheroidal cushion tissue (CT) cell aggregates and compared with the existing experiments and some published Monte Carlo results⁴⁵ (Figure 1). The KMC simulations were then used to quantitatively predict the time evolution of post printing tissue structures in several geometries relevant to animal organs or organ parts, such as rings (Figure 2), sheets (Figure 3), and tubes in the mammalian lung, or small capillaries of the vasculature.^3,31,40

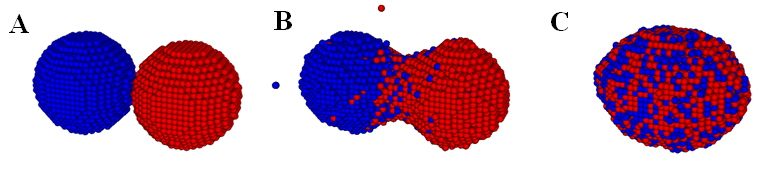
Figure 1 Time evolution of two fusing cellular spheroidal aggregates in a KMC simulation. The cells in the two identical aggregates are colored differently to emphasize their mixing during fusion. Initially, each aggregate contains 4140 cells. (Readers are referred to⁴⁵ for the corresponding experimental result).

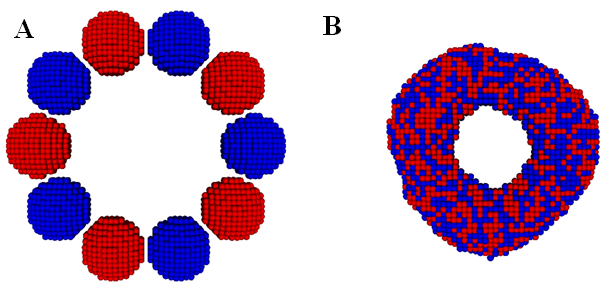
Figure 2 The initial (A) and final (B) state of a ring construct formation from fusion of ten spheroidal cellular aggregates in a KMC simulation. Note that all the cells are of the same type and the neighboring aggregates are colored differently to visualize their mixing. Initially, each aggregate contains 994 cells. (Readers are referred to³ for the corresponding experimental result).

Figure 3 The initial (A) and final (B) state of a tissue sheet formation via fusion of a single layer of deposited cellular spheroids in a KMC simulation. Note that all the cells are of the same type and the neighboring aggregates are colored differently to visualize their mixing. Initially, each aggregate contains 925 cells. (Readers are referred to³¹ for the corresponding experimental result).

We also used the KMC method to study the process of cell sorting within cellular aggregate fusion formed by multiple types of cells with different adhesivities. This study is directly related to biofabrication of a vascularized thyroid gland construct with two large-diameter vessels fabricated from vascular tissue spheroids made up of mixed smooth muscle cells (SMCs) and endothelial cells (ECs) (Figure 4).⁴⁶ The biological analogues of the structures with different types of cells are thick blood vessels, with ECs lining their interior wall and SMCs providing the contractile properties of the vessel, as well as extracellular matrix. To compare with the bioprinting experiment result, we have conducted an extensive model parameter search to produce most reasonable results. This makes the computational prediction extremely valuable.

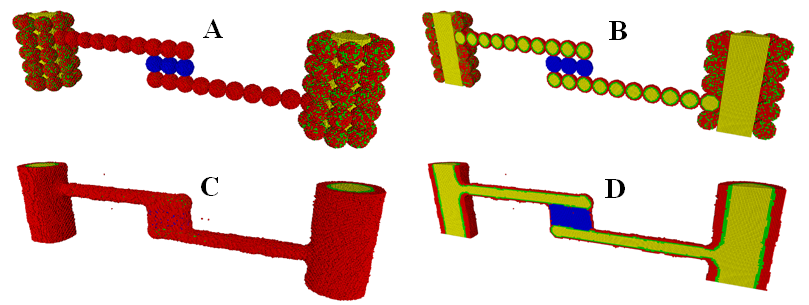
Figure 4 The initial (A,B) and final (C,D) state of the formation of a vascularized thyroid gland construct with two large-diameter vessels fabricated from vascular tissue spheroids in a KMC simulation. (A,C): The outer view. (B,D): The cross-sectional view. Smooth muscle cells (SMCs)are in red, endothelial cells (ECs)are in green lining the interior wall, internal hydrogel medium/lumen regions are in yellowand thyroid spheroids (TSs) are in blue. (Readers are referred to⁴⁶ for the corresponding experimental result).

Our research discussed here is a part of the South Carolina Project for Organ Biofabrication,⁴⁷ in which scientific progress includes computational modeling of vascular trees, fabricating and experimental testing of natural and engineered constructs, a working 3D bioprinter has been made. As the modeling and simulation core of the research thrusts, we focus on the development of the necessary predicative tools, including mathematical models and simulation tools, to support testing of the vascular constructs and prefabrication engineering design. Our research goals are to develop a simulation tool to predict the structure formation results during biofabrication and to help bioengineering researchers in their design and experiments. Our KMC simulation tool is thus developed against this backdrop and tested against available experiments and benchmarking simulations, for which some preliminary simulation results are given in.^40,41,46

We have used the kinetic Monte Carlo (KMC) method with a three-dimensional (3D) lattice model developed in⁴⁰ to study cell self-assembly and cellular aggregate fusion. Our work is motivated by the growing need to understand morphological changes and biomechanical properties of the engineered tissue constructs during their fabrication processes, which will have direct applications in tissue engineering and regenerative medicine, in particular, the emergent field of 3D bioprinting. Our simulations agree qualitatively with the experimental findings. These simulations not only explore the feasibility of bioprinting 3D constructs using multicellular spheroids, but also demonstrate the potential to aid engineering design in all steps of the biofabrication process using an in silico tool.

The research of YS is partially supported by the National Science Foundation (NSF) under grant number DMS-1318866 andDMS-1620212. The research of QW is partially supported by NSF under grant number DMS-1200487, DMS-1517347,NSFC grant #91630207 and # 11571032, and NSAF-U1530401. The authors thank Drs Christopher J Drake, Roger R Markwald, Vladimir Mironov, and Michael J Yost for their sharing of the experimental findings, vision, encouragement and guidance for this study.

The author declares no conflict of interest.