Advances in
eISSN: 2572-8490


Research Article Volume 1 Issue 1
1Department of Pathology and Laboratory Medicine, Rutgers University, The State University of New Jersey, USA
2Graduate Program in Biomedical Engineering, Rutgers University, USA
Correspondence: Frederick H Silver, Department of Pathology and Laboratory Medicine, Robert Wood Johnson Medical School, Rutgers, The State University of New Jersey, 675 Hoes Lane, Piscataway, NJ 08854, USA
Received: September 08, 2016 | Published: October 24, 2016
Citation: Silver FH, Shah R. Measurement of mechanical properties of natural and engineered implants. Adv Tissue Eng Regen Med Open Access. 2016;1(1):20-25. DOI: 10.15406/atroa.2016.01.00004
Numerous tests have been used to elucidate the mechanical properties of tissues and implants including tensile, compressive, shear, hydrostatic compression and three-point bending in one or more axial directions. The development of a non-destructive test that could be applied to tissues and materials in vivo would promote the analysis of tissue pathology as well as the design of implant materials.
In this paper, we review the methods that have been used to evaluate the mechanical properties of tissues and the invasiveness of these methods. There are several fairly new methods that have been evaluated in the literature such as magnetic resonance elastography (MRE), ultrasound elastography (UE), optical coherence tomography (OCT), ocular response analysis (ORA), optical coherence elastography (OCE) and OCT with vibrational analysis that are quite promising. Classical methods such as constant rate-of-strain deformation as well as incremental stress-strain analysis are useful but prove to be too destructive to tissue and therefore have limited value for measuring tissue properties in vivo.
While these newer techniques are very useful, they must be modified to consider viscoelastic effects of polymer behavior and compressibility that may occur during deformation in order to provide accurate information about implants and tissues. Non-linear behavior, strain-rate dependence and volumetric effects that occur during mechanical loading of tissues and implants are very important considerations in the measurement of mechanical properties of tissues and implants. Mechanical testing results obtained using these new methods must be compared and be consistent with “gold standard” results obtained from constant rate-of strain experiments.
Keywords: mechanical testing, modulus, extracellular matrix, tissues, implants, magnetic resonance elastography, optical coherence elastography, ocular response analyzer, ultrasound elastography
MRE, magnetic resonance elastography; UE, ultrasound elastography; OCT, optical coherence tomography; OCE, optical coherence elastography; ORA, ocular response analysis
Tissues transduce internal and external mechanical signals into changes in tissue metabolism that result in changes in structure and function through a process termed mechanochemical transduction.1,2 Mechanical loading plays a central role in vertebrate development, evolution, tissue maturation and development of tissue fibrosis during wound healing.1,2 Abnormal mechanochemical transduction processes may also lead to tissue fibrosis in diseases such as osteoarthritis.3 and cancer.4 Therefore, it is necessary to evaluate the mechanical properties of implants to begin to understand how their properties affect mechanochemical transduction of the surrounding tissues and the interaction with tissue engineered implants. Mechanical mismatch between host tissue and implants lead to intimal hyperplasia in vascular applications and the formation of tough capsules composed of extracellular matrix in areas such as the breast.2
Beyond the need to characterize mammalian tissues by mechanical means, it is important to be able to characterize implants that are used as replacements or to augment tissues.5 While the bulk of polymers used in medicine include, polyglycolic acid, polylactic acid, polydimethylsiloxane, polytetrafluoroethylene, polyethylene, polyacrylates, polyurethanes and natural polymers such as collagen, hyaluronan, alginates and silk,5 their properties vary extensively depending on how they are compounded and processed. Clearly the strength and stiffness of synthetic sutures, wound dressing materials, bandages, vascular grafts, and artificial valves are important parameters that need to be understood to prevent premature mechanical failure of medical devices.
The mechanical properties of implants and tissues has been the subject of extensive research and books.5–7 These properties support the proper physiological function in many applications including Cardiology, Dermatology, Neurology, Ophthalmology, Orthopedics, Urology and many other disciplines in medicine. For example, energy storage, transmission and dissipation by tendons in the musculoskeletal system, by the pericardium that surrounds the heart, and the duramater, that covers the brain, are important in preventing stress fractures, cardiac dilatation, and brain injuries, respectively.1,8 For this reason, improved methods are needed to study the mechanical properties of tissues and implants. Yamada.6 published a pioneering textbook describing the strength of tissues that has been an important reference in this field. Most of the early measurements were made using uniaxial deformation at a constant rate-of-strain. Later studies suggested that tissues were viscoelastic and therefore their properties were dependent on the rate of deformation. The viscoelasticity of tissues and polymers has made analysis of the mechanical properties of these materials more complicated7 but the application of incremental stress-strain experiments has resulted in the ability to correct mechanical measurements for time-dependence and viscoelasticity8 (Figures 1) (Figures 2). Correction for the time-dependence is accomplished by breaking the stress into an elastic component and a viscous component8 (Figures 3). The elastic component for ECM has been shown to be strain-rate independent while the viscous contribution varies based on the strain-rate of testing.2 Therefore, meaningful measurements of the mechanical properties of tissues containing collagen can be accomplished by measurement of the elastic modulus.1 All other measurements are subject to strain-rate dependence; the “apparent” modulus increases with increased strain rates9 leading to modulus values that are variable and not material constants.
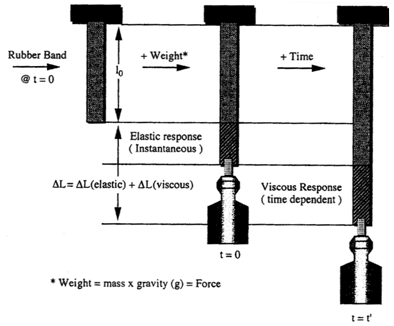
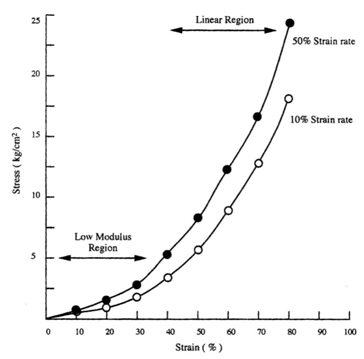
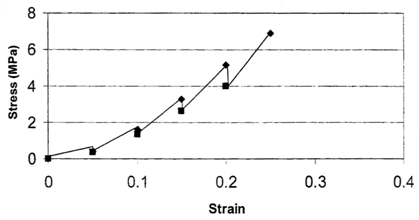
Most mechanical tests require use of stresses and strains that cause permanent damage to tissues and implants. While ultrasonic10,11 and elastographic measurements12,13 do not destroy tissue, these measurements require use of models for tissue behavior that assume linear Hookean behavior (stress and strain are linearly related) and incompressibility (Poisson’s ratio of 0.5), two assumptions that lead to incorrect determinations of mechanical parameters7 Therefore, there is a need to develop methods that can be used to measure the elastic modulus of tissues and implants that is non-destructive and can be corrected for viscoelastic behavior. The purpose of this review is to examine:
Theory of mechanical properties of materials
For the simplest loading condition in a single direction of an ideal material, the stress (force per unit area) and the strain (natural log of the change in length divided by the original length) are linearly related through a constant termed the modulus or stiffness (E) as indicated in (Equation 1).
Stress=ExStrain [1]
This assumes the material is homogeneous (behaves identically in all three geometric directions), that the stress and strain are linearly related (linear Hookean behavior) and that the material properties are not dependent on the time of observation. However, tissues and implants do not follow these assumptions: their behavior is non-linear, they are non-homogenous, and the behavior depends on the time of observation (Figures 1 through 4). Therefore, the use of (Equation 1) to analyze the behavior of tissues and implants is severely limited since measurement of a modulus that is dependent on the time of observation and extent of loading severely challenges the accuracy of the results. In addition, the use of (Equation 1) or a similar equation that assumes that the material deforms without a change in volume (Poisson’s ratio of 0.5) also presents an accuracy challenge since it has been observed that Poisson’s ratio differs greatly from 0.5 for tissues. The reported values of Poisson’s ratio vary from 0.125 for nucleus pulposus14 to 1.87 for the surface zone of human femoral cartilage.15 Therefore, any methods that make the assumptions of:
Correction of the measurements for the elastic component of the observed stress or force8 and correction for the change in volume that occurs during deformation is necessary to get accurate results. Keeping this in mind, below we will consider the methods used to determine the mechanical properties of tissues and implants.
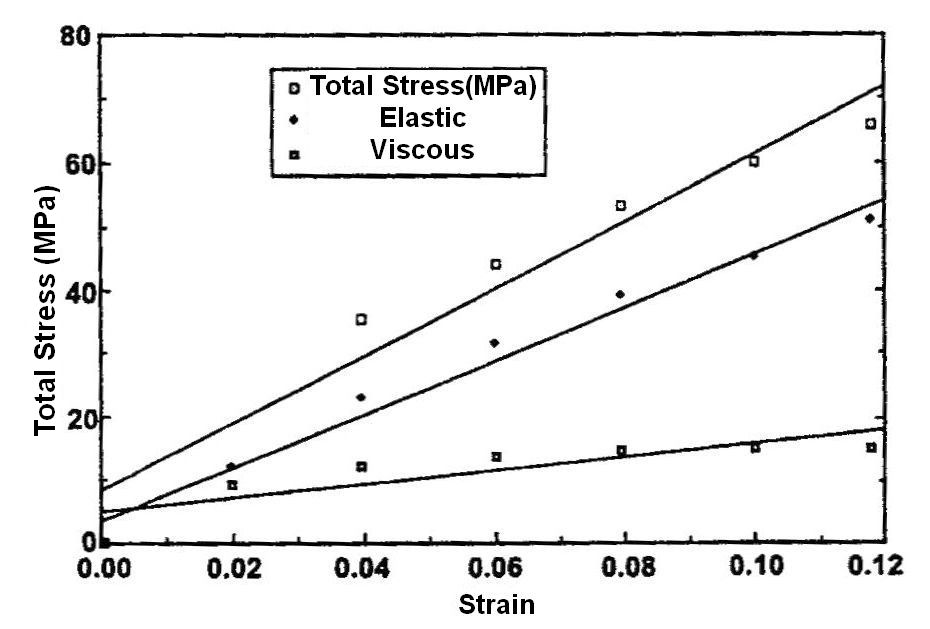
Methods for mechanical testing of tissues and implants
Constant rate-of-strain experiments: Traditionally, tissues and implants have been tested using constant strain-rate experiments where a sample is deformed at a constant rate until failure occurs either in tension or compression (Figure 2) (Table 1). The modulus (E) is obtained from the slope of the stress-strain curve and does not require assuming a value of Poisson’s ratio. The test requires mounting the sample ends in grips and is usually conducted until the sample fails in tension (Figure 2). As pointed out in Figure 2 the slope (E) depends on the rate of deformation. As the sample is stretched at a higher rate of strain, the modulus appears to increase because the sample does not have time to relax during deformation. This test can be done in one or more loading directions and can be repeated many times during fatigue tests in tension and compression. The limitations to this test are:
Method |
Selected reference |
Limitation of results |
|
Contact manipulation |
Sugimura et al.16 |
Can be invasive |
|
Constant-rate-of strain |
Yamada.6 |
Destructive testing |
|
Incremental stress-strain |
Dunn & Silver.8 |
Destructive testing |
|
Magnetic resonance elastography |
Low et al.17 |
Assumes hookean behavior & incompressibility |
|
Ocular response analyzer |
Ruberti et al.18 |
Measures deflection of tissue |
|
Oil microdroplet formation |
Campas et al.19 |
Determines local forces |
|
Optical coherence elastography |
Kennedy et al.12 |
Assumes hookean behavior &, incompressibility |
|
Wang & Larin.20 |
|||
Uniaxial tensile loading |
Yamada.6 |
Destructive testing |
|
Ultrasound elastography |
Zaleska et al.22 |
Assumes hookean behavior & incompressibility |
|
Vibrational analysis and OCT |
Li et al.23 |
Does not measure E directly |
|
|
Shah et al.25 |
Destructive testing |
|
Table 1 Selected methods used to measure the mechanical properties of tissues
Incremental stress-strain tests: This test is conducted in tension or compression in a very similar manner to constant rate-of–strain methods except the sample is loaded in strain increments as shown in (Figure 3) (Figure 4)2,8 (Table 1). After each strain increment the sample is allowed to relax under tension or compression until it reaches its final dimensions. At that time another strain increment is added and the process is repeated. The data is plotted both as a total stress-strain curve and an elastic stress-strain curve (stress after relaxation has occurred) similar to that done in constant rate-of-strain experiments. The elastic modulus is obtained from the slope of the stress-strain curve after relaxation has occurred. It turns out for several collagenous tissues the elastic modulus is strain–rate independent2 and the elastic component contributes between 50 and 70% to the total stress depending on the degree of orientation of collagen fibers8 The value of this method is that it gives an elastic modulus value that is a material property (not strain-rate dependent) but the test also requires destruction of the tissue. It should be noted that relaxation of the material to equilibrium at each step may require up to 24 hrs and is a time consuming process.
Contact manipulation methods: Sugimura et al.16 review methods for measuring forces and stresses in situ in living tissues by applying physical forces. The methods require a pushing, pulling, applying light energy, ablation of tissue using lasers, applying liquid droplets and measuring quantities such as the birefringence of anisoptropic tissues to evaluate the tissue reaction to applied forces. This approach gives values of local mechanical influences on tissues based on the reaction to applied forces. The results may be difficult to interpret in terms of standard mechanical parameters, such as the modulus, since the measurements are made under local non-equilibrium conditions. The method also requires destruction of the tissue in some cases.
Magnetic resonance elastography (MRE): Low et al.17 review the use of magnetic resonance to calculate values of the modulus of tissues. In this method, mechanical excitation is produced by pneumatic, electromechanical, or piezoelectric stimulators positioned next to the body. The tissue is loaded by one of these means and then the MRI signal is collected. The phase shift in the MRI signal is used to calculate a value of the modulus; however, the workers assume that Poisson’s ratio is 0.5 and that the tissue density is 1.0g/cc. These assumptions create calculation errors since Poisson’s ratio has been shown to vary from 0.5 for tissues. The value of this technique is that it can be used non-invasively in real time; however, use of this technique requires correction for Poisson’s ratio and strain-rate effects to be entirely accurate.
Ocular response analyzer (ORA): The Ocular response Analyzer is a clinical device that uses a high speed air puff to deform the cornea. Changes in shape of the anterior surface are tracked using an infrared beam reflected from the surface and aligned with the geometry of a detector.18 In this technique corneal deformation is tracked after the air puff is applied to the corneal surface. Differences in the pressures between the inward and outward flattening of the cornea are reported as the corneal hysteresis. Changes in the corneal hysteresis are correlated with disease states anecdotally. The non-invasiveness of this technique is a positive attribute of this method. However, the inability to relate the results to standard mechanical testing parameters limits the utility of this method.
Oil microdroplet deformation: Campas et al.19 describe a method for determining cell-generated mechanical forces within living cells by introducing an oil droplet coated with biologically compatible molecules between cells. These workers use fluorocarbon oils immiscible in vegetable oils and stabilize the droplets using a biocompatible surfactant. The internal tension in the droplet is adjusted to allow measurement of the stresses applied by different types of cells. The geometry of the droplet is related to the local cellular forces through Laplace’s Law. Equations are developed that relate the droplet shape in 3D and the anisotropic stresses responsible for inducing the deformation. Oil droplet shape changes are introduced into these mathematical models to calculate intercellular forces and estimate the mechanical interactions that occur in living systems. The authors confirmed with this technique that stresses generated by mammary epithelial cells are myosin II-dependent and more than 2-fold larger than those generated by tooth mesenchymal cells.
This is an interesting approach to measure local forces that can be combined with other more macroscopic methods to collect mechanical data on both local and macroscopic properties of cells and tissues. A consideration of the mathematics of the approach used in interpreting the results is that it gets complicated when one is working in three dimensions with non-uniform cell morphologies.
Optical coherence elastography (OCE): Kennedy et al.12,13 & Wang et al.20 have recently reviewed the use of optical coherence elastography for the analysis of tissue mechanical properties. This technique uses light that is reflected off a surface and compared to the non-reflected light to create an image and to measure displacement after the tissue undergoes a small displacement. Mathematical modeling is used to calculate the tissue modulus assuming the tissue is a linear elastic solid and that Poisson’s ratio is 0.5. This technique is non-invasive and can be used to evaluate tissue in situ. However, the values of moduli obtained from the models used appear lower than those calculated from destructive testing, suggesting that the strains introduced are not large enough to deform the structural components of the tissue.
Ultrasound elastography (UE): Drakonaki et al.21 point out that ultrasound elastography is referred to by a number of terms including strain elastography, compression elastography, sonoelastography, and real-time elastography. Using these techniques a low frequency compression is applied to the tissue, frequently via the hand held transducer. The applied compression induces a strain and the modulus is estimated from the change in the echo before and after the force is applied. Zaleska-Dorobisz et al.22 & Low et al.17 review the use of ultrasound to calculate the modulus values of tissues for different clinical applications. This technique assumes that the tissue is a linearly elastic solid that has a Poisson’s ratio of 0.5 and does not measure the modulus directly. Clinically, this technique has been used to identify pathologic changes in a number of diseases. However, the data obtained from UE will depend on the frequency of sound used in the measurements and the assumptions made in converting the displacement to elastic modulus.
Ultrasound devices equipped with a sonoelastography option enable more accurate imaging and evaluation of the nature of lesions situated at small depths beneath the tissue surface in breast, thyroid, testicles, prostate and some groups of lymph nodes.22
Vibrational analysis and ocular coherence tomography (OCT): Li et al.23 report creation of a surface wave in the cornea and evaluation of the mechanical properties using surface wave velocity measurements. They use pulsed laser excitation to create a surface wave and estimate the modulus from an equation that relates the surface wave velocity to the modulus. Song et al.24 use ultrasound to create a shear wave and used OCE to measure the properties of tissue. The above studies assumed a value for Poisson’s ratio and a density to calculate the mechanical properties. The assumption of a value of 0.49 for Poisson’s ratio leads to calculation errorsas discussed above. These methods are non-invasive and if modified to correct for viscoelasticity and incompressibility would give improved results.
Shah et al.25 used vibrational analysis in concert with OCT to measure the natural frequency of decellularized dermis (Figure 5) and silicone rubber. They applied an acoustic vibration to the samples under tension and showed that the natural frequency squared obtained from the change in frequency of the reflected light was directly related with the tensile modulus obtained in an incremental stress-strain experiment, Moduli data from vibrational analysis compared very well to moduli obtained from incremental stress-strain curves (Table 2). Their method did not rely on the assumption of a value of Poisson’s ratio; this technique would be of value clinically if the measurements could be made non-invasively in situ.
Material |
Cycle |
Tensile testing modulus |
Vibrational analysis modulus |
Dermis |
1 |
5.04 MPa |
5.79 MPa |
|
2 |
4.90 MPa |
5.79 MPa |
Table 2 Moduli for decellularized dermis loading cycle. Results derived from the loading portion of the tensile stress-strain measurements and vibrational analysis for the first and second loading cycle at 12% strain. Note the similarity between modulus values measured using incremental stress-strain curves and vibrational analysis Shah et al.25

Non-destructive and non-invasive characterization of tissues and implants has been an important goal for researchers for decades. Unfortunately, the use of ultrasound and elastography provide only estimates of the exact values of mechanical parameters such as the modulus.10–13 OCE has been recently applied to studying tissue properties in health and disease; however, the values reported for tissue moduli are in the kPa range12 as opposed to the MPa range that is expected for biological polymers.2,9,26 These methods would be very useful if the techniques would use models that give similar results to those obtained from in vitro constant rate-of strain measurements after strain-rate and volume effects are considered.
Several diseases such as Osteogenesis Imperfecta11 and tumor differentiation27 are characterized by changes in the mechanical properties such as modulus and hardness. However, it is important to be able to accurately calculate the value of the modulus since the modulus depends on the exact composition of the macromolecular components, their orientation and the degree of cross linking of the components.5 The use of vibrational analysis and OCT if accomplished non-invasively might give values of the mechanical properties that are comparable to results of constant rate-of-strain measurements made in vitro.
In this paper, we review the methods that have been used to evaluate the mechanical properties of tissues. There are several new methods such as MRE, UE, OCE, ORA, and OCT combined with vibrational analysis; techniques that are quite promising. However, for these techniques to provide accurate information about implants and tissues they must consider non-linear behavior, strain-rate dependence and volumetric effects that occur during mechanical loading. It is well known that fluid flow during cartilage and bone deformation is an important mechanism for energy dissipation as well as a stimulator of tissue mechano transduction.28,29 Fluid flow from tissues under load is an important contributor to non-linear viscoelastic behavior. To ignore these effects limits the relevance of any technique used to determine the mechanical properties and may limit the accuracy of these techniques.
While the reported literature values of moduli for a single tissue may vary,20 it is important to consider that the reported values are meaningless unless the rate-of-strain is reported and other sample parameters are known. For instance, it is well known the mechanical properties of skin depend on sex, age, rate-of-strain, sample orientation, sample location, exposure to sun-light or damaging chemicals as well as disease states such as diabetes.2,9 Therefore, all these parameters must be controlled in order to evaluate tissue and implant mechanics non-invasively. While this is an enormous task, the goal of using mechanical measurements to evaluate tissue and implant property changes and disease progression makes this an important issue.
None.
The author declares no conflict of interest.

©2016 Silver, et al. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.