Aim: A relationships between sap flow and stem diameter change with weather parameters included in ET0 calculation have been reported by numerous authors. Thus, we can assume that there is a statistical interdependency between a series of chronologically recorded of physiological indicators and a simultaneously time spaced ET0 data. To demonstrate our assumption and for quantification of the interrelationship between the series, we used time series of sap flow and diameter change of grapevines together with an ET0 series of the vineyard location to perform an event coincidence analysis.

Methods and results: Two sets of six grapevine each, one irrigated and the other rainfed, were fitted with dendrometer and sap flow needles and their fluxes of sap (SF) and their maximum daily shrinkage (MDS) of the trunk were recorded during 5years from 1 June to 30 September. During the same period, an automatic weather station collected weather data to calculate the reference evapotranspiration (ET0). Stomatal conductance (gs) was measured at solar noon twice a month. Averages of SF, MDS and gs were significantly different between irrigated and rainfed grapevines. The correlations between SF, MDS and ET0 were significant and both high and low ET0 events triggered directly corresponding SF and MDS events but not both simultaneously as shown by a statistical procedure named event coincidence analysis.

Conclusions: SF and MDS are related to different physiological processes and have a differentiated response to the main weather parameters that drive the ET0. SF or MDS as single descriptor does not reflect the grapevine response to changing environmental conditions but their combination can provide more detailed information about its water needs. Significance and impact of the study: This study highlights the advantages and limitations of SF and MDS as descriptor of the grapevine water needs and their relationship with atmospheric environment.

Keywords: event coincidence analysis, stomatal conductance, sap flow, maximum daily shrinkage, reference evapotranspiration, vitis vinifera

ECA, event coincidence analysis; ET₀, reference evapotranspiration; Gs, stomatal conductance; K, observed number of events; K_e, expected number of events; MDS, Maximum Daily Shrinkage; Q₁, first quartile; Q₄, forth quartile; SF, sap flow

The use of plant-based water status indicators is today very common because the plant itself is the best indicator of its water status, the data acquisition at a high resolution across larger temporal scale and its analysis is now more affordable, and plant water status controls many physiological processes and crop productivity, thus this information has great practical interest for crop management, in particular the water management. Grapes are widely cultivated worldwide but they are concentrated in Mediterranean type climates where water is scarce and face increased competition with other stakeholders.

For these reasons but also because water influence vegetative growth and reproductive growth, yield and berry composition through their effects on berry size and on photosynthetic activity, vineyard water management has received great attention.^1,2 Vineyards managers try to maximize the water use efficiency at the cost of some reduction in crop yield that is not detrimental for the wine makers as the highest crop loads are linked to low grape quality, in fact, limitations to grape yield are a common practice for a market standard wine production and premium wines.³ To determine the influence of environmental and cultural conditions on vine water use and the grapevine water status, and to manage water in the vineyard, one must use both a physiological indicator that integrates environmental conditions and tools to evaluate water use.⁴

A common and widely use indicator of plant water status is stomatal conductance (gs) that can be a precise indicator in grapevines³ but gs readings cannot be automated and a very limited number of observations can be made at a given time and location. However, several authors have found a relationship between gs and other water status indicators, such as sap flow and changes on diameter of plant organs, and also to evapotranspiration.^5–7 For grapevines and fruit trees, indicators derived from measurements of sap flow rate and diameter changes in conductive organs, normally the trunk, are considered good predictors of plant water status.⁸ These indicators can be continuously and automatically recorded with high resolution^9,10 and are reported to be closely related to climatic variables such as solar radiation,¹¹ temperature,¹² vapor pressure deficit¹³ and evaporative demand of the atmosphere.² The evaporative demand of the atmosphere at a specific location is evaluated by the reference evapotranspiration (ET₀) that integrates several weather parameters¹⁴ that affect sap flow and diameter changes. Given the relationships between sap flow and diameter change with weather parameters included in ET₀ calculation that have been reported by numerous authors, we can assume that there is a statistical interdependency between a series physiological indicators chronologically recorded and a simultaneously time spaced ET₀ data. To demonstrate our assumption and for quantification of the interrelationship between the series, we used time series of sap flow and diameter change of grapevines together with an ET₀ series of the vineyard location to perform an event coincidence analysis (ECA).¹⁵ This study is expected to highlight the advantages and limitations of SF and MDS as descriptor of the grapevine water needs and their relationship with atmospheric environment.

Field description

The experimental field was set up in 2011 in a vineyard at the campus of University in Vila Real, Portugal (41.285431N, -7.738142W). The 15 years old vineyard of Vitis vinifera L. (cv. Touriga Nacional) trained as vertically positioned shoots, it was commercially managed, it had a total area of 0.8 ha, it was planted in a gently sloping land (<2%) and it was spaced 2m between rows and 1m between adjacent plants. When the canopy was fully formed, the shoots were pruned to maintain the rows at maximum height and depth of 1.80m and 0.7m, respectively. The soil is a Cambisol dystric [16] with a regular depth of 0.8m. The weeds below the row were removed by shallow tillage when necessary and those between rows were mowed regularly.

Data collection

Two sets of six adjacent plants each, disease free and about the same size, were chose 12 meters apart. One set was rainfed and the other was irrigated weekly from June to September with 40% of the ET₀ calculated for the previous week. The trunk of two vines on each set was fitted with a dendrometer (Ecomatik DD-L, ECOMATIK Muenchner Str. 22 D-85221 Dachau/Munich, Germany) 10cm above the grafting point and with a sap flow needles (Thermal Dissipation Probe, Dynamax Inc. Fallstone Houston, USA) about 20cm above the dendrometer and insulated from rapid temperature changes as recommended by the equipment maker. Every year, the sap flow needles were removed (also the dendrometer) and placed in an adjacent plant to reduce serious head injuries on the trunk tissues.

An in situ meteorological station (Skye Instrument, Llandrindod Wells, Powys LD1 6DF, UK) collected weather data. Sap flow needles, dendrometer and the meteorological station were linked to a data logger (DL2 - Data Logger, Delta-T Devices Ltd, 130 Low Road Burwell, Cambridge, CB25 0EJ, UK) that took readings every five minutes and recorded the average over 30 minutes intervals. The data was collected every year from 2011 to 2015 starting 1 June (DOY 121) to 30 September (DOY 273) that comprises the flowering stage (usually during the second week of June) and the period about two weeks before commercial harvest.

Reference evapotranspiration was calculated at daily intervals (mm day^-1) as follows¹⁴

$E{T}_0=\frac{0.408△\left(R_n-G\right)+\gamma \left(\frac{900}{T+273}\right)u_2\left(e_s-e_a\right)}{△+\gamma \left(1+0.34u_2\right)}$ (1)

where R_n is the net radiation at the surface (MJ m⁻²day⁻¹), G is the soil heat flux (MJ m⁻²day⁻¹), T is the mean air temperature at 2 meters height (⁰C), u₂ is the wind speed at 2m height (m s⁻¹), e_s is the saturation vapor pressure (kPa), e_a is the actual vapor pressure (kPa), e_s−e_a is the saturation vapor pressure deficit (kPa), D is the slope vapor pressure curve (kPa⁰C⁻¹), and g is the psychometric constant (kPa⁰C⁻¹). Individual daily vine transpiration (L day^-1) was calculated from the procedure described by Davis¹⁷ and Dynamax.¹⁸ Dendrometer raw data was used to derive the descriptors depicted in (Table 1).

During the first year, one grapevine apart from the others under observation was fitted with a dendrometer and irrigated weekly from May to September to 90% of ET₀ calculated for the previous week and we considered this vine at non-limiting soil-water conditions. Higher amount of irrigation would waterlog the soil for too long time periods. The dendrometer raw data was used to obtain the reference values for each of the descriptors mentioned in (Table 1). The quality of the descriptor was defined by its sensitivity that assesses the usefulness of the water-stress indicator¹⁹

$Sensitivity= \frac{Signal Intensity}{CV}$ (2)

Where CV is the coefficient of variation and

$Signal Intensity= \frac{Actual value of the predictor}{Reference value of the predictor}$ (3)

The sensitivity of MDS (3.66) was higher than of any other indicator, thus, its time series was the only one to describe the trunk diameter variation of the grapevines. The time series for MDS and sap flow (SF) were obtained by averaging the data from two plants on each set. The series (MDS, SF, ET₀) had a total of 765 observations each and a standard correlations test (two tailed Pearson) was performed to quantify the direction and significance of the linear association between the variables. The low and the high values of ET₀ are of particular importance as they might drive larger differences on both MDS and SF in relation to their averages. Each series was subdivided in their quartiles and ECA was performed only on the sub-series corresponding to the first (Q₁) and forth (Q₄) quartiles, like a procedure used by Siegmund.²⁰ The notation

For each series is as follows:

1. First quartile SF irrigated plants            Q₁SF_i
2. Forth quartile SF irrigated plants             Q₄SF_i
3. First quartile SF rainfed plants             Q₁SF_r
4. Forth quartile SF rainfed plants             Q₄SF_r
5. First quartile MDS irrigated plants             Q₁MDS_i
6. Forth quartile MDS irrigated plants             Q₄MDS_i
7. First quartile MDS rainfed plants             Q₁MDSr
8. Forth quartile MDS rainfed plants             Q₄MDS_r
9. First quartile ET₀                  Q₁ET₀
10. Forth quartile ET₀                       Q₄ET₀

Every first and third week of each month from June to September on clear sky days, one adult leaf on the middle of a shoot per plant on each set was chose to determine stomatal conductance (gs) (AP4 parameter, Delta-T Devices Ltd, 130 Low Road Burwell, Cambridge, CB25 0EJ, UK) at solar noon. A total of 240 gs readings were recorded per set during the duration of the experiment. Pearson correlation was also calculated between gs and SF, MDS. Given the disparity on the number of observations among these variables, a single value for gs was obtained averaging the six readings on each set on a given date that was paired with the corresponding SF and MDS values for the same date.

Event coincidence analysis (ECA)

A detailed explanation of this procedure can be found in Donges¹⁵ & Siegmund²⁰ that is concerned with quantifying the statistical interrelationships between pairs of event series where the event time series A and B are defined as two ordered sets t_1A,…., t_NA and t_1B,… t_NB with numbers of events N_A»1 and N_B»1, respectively, covering a time interval T. The assumption to be tested and quantified is that events B precede events A because there is a cause-effect relationship between them (Figure 1).

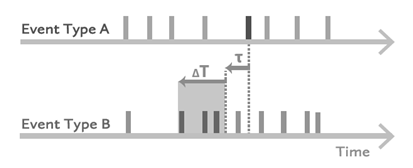
Figure 1 Schematic illustration of event coincidence analysis for quantifying statistical interrelationships between two event time series A and B for the case of precursor coincidences.¹⁵

An instantaneous coincidence occurs if two events at t_iA, t_jB with t_jB< t_iA are closer in time than a coincidence interval DT (t_iA - t_jB ≤ DT). A lagged coincidence is an instantaneous coincidence between the time shifted event at t_iA-t, where t ≥0 is a time lag parameter, and the event at t_jB< t_iA-t ((t_iA-t)- t_jB ≤ DT). Assuming that both A and B type events are generated by Poisson processes with event rates l_A = N_A/T and l_B = N_B/T, respectively, both types are distributed randomly, independently and uniformly over the continuous time interval of length T. The probability for a lagged precursor coincidence between an A-event and a preceding B-event is given by

$p= \frac{△T}{T-\tau }$ (4)

$1- {\left(1-p\right)}^{N_B}$ (5)

The probability of K precursor coincidences are observed for a given realization of two Poisson processes is

$P\left(K;N_A,1-{\left(1-p\right)}^{N_B}\right)=\left(\begin{array}{c}{N}_A\\ K\end{array}\right){\left(1-{\left(\frac{△T}{T-\tau }\right)}^{N_B}\right)}^K{\left(\left(1-{\left(\frac{△T}{T-\tau }\right)}^{N_B}\right)\right)}^{N_A-K}$ (6)

If the events type A are spaced much wider than the coincidence interval, i.e.

$△T\ll \frac{T}{N_A}$ (7)

The expected value for K is then

$K=N_A\left(1-{\left(1-p\right)}^{N_B}\right)$ (8)

And the standard deviation is

$\sigma \left(K\right)=\sqrt{N_A\left(1-{\left(1-p\right)}^{N_B}\right){\left(1-p\right)}^{N_B}}$ (9)

Then the expected value of the precursor coincidence rate is

$r_p=\frac{K}{N_A}$ (10)

And the standard deviation

$\sigma \left(r_p\right)=\frac{\sigma \left(K\right)}{N_A}$ (11)

The probability of obtaining a number of coincidences K larger or equal to the empirically observed number K_e is given by

$P\left(K\ge K_e\right)={\displaystyle \sum }_{K=K_e}^{N_A}P\left(K;N_A,1-{\left(1-p\right)}^{N_B}\right)$ (12)

To conform to equation,⁷ DT was set up at value 1, consequently t=0, testing that both SF and MDS events (Type A) were triggered by the closest ET₀ events (Type B). To transform the SF, MDS and ET₀ time series into event time series, we applied the first and the fourth quartile threshold creating series for values of those variables that were either smaller or larger than the thresholds and recorded as 1 (true) or 0 (false).

The predictors of the water status of grapevines (gs, SF, MDS) could clearly tell apart the ones that were irrigated from those that were rainfed. The overall average of stomatal conductance showed a highly significance (P<0.01) difference between the values read for the irrigated set (gs=2.64 cm s^-1) and the rainfed set (gs=1.89 cm s^-1). The trunk MDS and SF averages showed highly significant differences between both sets of plants, respectively, 57.6 mm and 4.2 L day^-1 plant^-1 for the irrigated and 61.8 mm and 2.7 L day^-1 plant^-1 for the rainfed. The overall average for crop load at harvest of irrigated plants was 2863 g per plant and the rainfed was 2054 g per plant. Reference evapotranspiration average was 1.62 mm day^-1 and no significant (P>0.05) correlation was found between gs and ET₀. However, on (Table 2) can be seen that the correlations between ET₀ and both MDS and SF were significant for both water regimens. The correlation between gs and both SF and MDS, both water regimens, were not significative as shown in (Table 4). ECA analysis was performed only between variables that were significatively correlated. The results of ECA are shown in (Tables 5 & 6) and they did not distinguished between rainfed (_r) and irrigated (_i) plants. The closest ET₀ event to SF or MDS always triggered an empirically observed number (K) for SF or MDS that was significatively higher than the expected coincidence (K_e) if the process was purely random. Lower values (Q₁) of ET₀ triggered lower values of both SF and MDS and, conversely, higher values (Q₄) of ET₀ triggered higher values of both SF and MDS (Table 5). The ECA showed that ET₀ events could not trigger simultaneously either higher or lower values for SF and MDS as K was always much lower than K_e (Table 6).

Several authors have considered gs, SF and MDS as good predictors of the plant water status.^9,7,21 The results show these predictors could distinguish between irrigated and rainfed plants and they are in agreement with a large body of bibliographic references. The discrepancies appear when the relationships among these predictors and between them and environmental factors are established. Environmental conditions affect the physiological activity of plants altering their transpiration through stomatal control which must influence the sap flow rate²² that should decrease under high atmospheric demand because augmented stomatal resistance reduces transpiration.⁵ A close relationship between SF and gs was found by Hernandez-Santana²¹ if multiple readings of gs from several leaves were taken during the day. The results of this work failed to establish a significant correlation between gs and SF and the reason must reside on the measurement particularities of each variable.

SF integrates multiple readings taken and recorded automatically during 24 hour periods while gs represents a specific value on a given time, thus, SF integrates constant changes of influential factors and gs represents the prevailing conditions of a given moment. There is no proved method of automatically measuring gs and to take multiple readings along the day is too taxing on resources. The relationship between MDS and gs, found by different authors, is sometimes contradictory. A significant, linear and direct relationship between MDS and gs was found in apple trees (28) and in olive trees ²³ but they were inversely related in cherry trees.²⁴ It appears unquestionable that the stem diameter variation can be related to plant growth, water-use and status but any possible correlation with gs is likely to be indirect.³ The lack of correlation between MDS and gs in this work is, again, on the specifics of their measurement process.

A large degree of agreement between daily reference evapotranspiration and SF has been found^25,26 and in olive trees the relationship was significant for both well-watered and water shorted plants.²⁷ A significant correlation was also found between MDS and ET₀ in apple trees²⁸ and in peach trees.²⁹ However, there is no full agreement on which weather meteor integrated in ET₀ calculation is the main underlying factor driving SF and MDS. Photosynthetically active radiation (PAR) and vapor pressure deficit (VPD) were the main drivers of SF in conifers¹³ and in a desert shrub,²⁶ while solar radiation and air temperature were found to be main driving forces in olive trees.³⁰ In vineyards,³¹ daily SF rate increased linearly with solar radiation and it showed an exponential increase with VPD or, for well-watered grapevines, SF increased linearly with VDP³² and in olive trees³³ SF was largely controlled by VDP. Regarding MDS of peach trees, the best predictor found was either VPD²⁹ or it was the minimum and maximum temperatures.¹⁴ In table grapes, at early stages of fruiting, mean temperature was the environmental variable that best correlated with MDS while in later stages was reference evapotranspiration and mean daily VPD.² In lemon trees, SF was more closely correlated with changes in reference evapotranspiration while MDS behavior was best correlated with mean daily air temperature.⁹

Other factors besides weather conditions, such as soil water availability, species, tree age, phenological period and crop load, affect SF and MDS and a single or a couple of weather variables do not correlate well with SF or MDS in all circumstances. The results show a significative correlation of MDS and SF with ET₀ but it was independent of the phonological period (Table 3) or the irrigation regimen (Table 2). Given that the crop load was larger in irrigated plants than in rainfed, we can assume that the correlation was also independent from the crop load and Intrigliolo and Castel³⁴ also found that the crop load did not affect the variation in trunk diameter. The soil water content affected the dimension of MDS because in rainfed plants it averaged 61.8mm while in irrigated plants it was 57.6mm; the difference must be due to a larger availability of soil water that irrigated plants can draw and it prevents a strong shrinkage of inner tissues and also helps the full recovery of the tissues hydration when transpiration is low. The roots of plant with more limited water supply might not be able to meet the transpiration needs and the internal water storage pool is depleted resulting in a larger shrinkage of the plant organs.³⁵

SF reflects the flow of water from the soil to the plant and to the atmosphere thru the stomata. This flow is largely controlled by stomatal conductance⁷ that the results show to be systematically higher in irrigated vines, thus they can experience higher values of SF as it was found by Hernandez-Santana.²¹ The correlation (Tables 2 & 3) show a direct relationship between MDS and SF and (Table 5) shows that both higher and lower values of ET₀ are also directly related to values of MDS and SF. The observation by De Swaef³⁶ that transpiration-driven sap flow rates are typically inversely related to stem diameter changes, except under conditions of low transpiration, does not hold in this case. More likely, increases in the evaporative demand induced more negative stem water potentials and SF increased, which determined an increase in MDS if soil water is not strongly depleted.⁹

All three types of stomata (sunken, same level and raised above epidermis) are present on the leaf lower face of Touriga Nacional grapevines, but same level and raised are dominant (about 54 and 47%, respectively) and they are, in comparison with other red varieties, longer (24 to 30 mm) and wider (17 to 18 mm) that might contribute to the enhanced plasticity of stomatal conductance under higher temperatures.³⁷ Touriga Nacional has high capacity for heat dissipation, it withstands high light intensities, it is well adjusted to warm conditions³⁸ and it can behave as isohydric.³⁹ Measured MDS and SF maintained a direct relationship between them and with ET₀ under the environmental conditions of the experimental field where the soil water content, even for rainfed plants, might never reached a lower threshold.

An ET₀ event, either low or high value, does not trigger, simultaneously, a corresponding SF and MDS event (Table 6). It means that SF and MDS respond differently to weather conditions. Similar values of ET₀ can be reached with different combinations of its main driving factors: solar radiation, vapor pressure deficit and temperature. ECA does not explain the underlying mechanisms between ET₀ and SF and MDS, rather establishes a stochastic relationship of casualty, but given the conclusions draw by other authors mentioned above, we might assume that the trigger ET₀ event was due predominately by one of its main driving factors that affects preferentially either SF or MDS. We must keep in mind that SF and MDS are related to different physiological processes.¹⁹ The variation of trunk diameter is, predominantly, the result of dynamics in water transport between tissues and depends mainly on the water stored in the phloem and in the outer xylem, while SF depends essentially on the level of hydration of the whole sapwood.⁴⁰

SF is a transpiration driven phenomenon and as transpiration progresses the hydraulic resistance throughout the plant increases causing the xylem water potential to decrease, influencing the water potential gradient between xylem and storage tissues, which has a direct effect on the radial water flow between these tissues.^10,41 This higher gradient decreases the radial conductance to water transport between the xylem and the storage tissue enhances the time lag between transpiration and diameter variation dynamics.⁴⁰ The relationship between ET₀ and the plant indicators might not follow the same pattern being linear with MDS and curvilinear with SF,⁵ resulting also in a time lag between MDS and SF. SF and MDS are good predictors of the plant water status⁹ but the results show that a single indicator, either SF or MDS, does not reflect the grapevine response to changing environmental conditions but their combination can provide more detailed information about its water needs. The same observation was made by Fernández⁸ regarding the water needs of mature olive orchards.

The predictors of the water status of grapevines (gs, SF, MDS) could clearly tell apart the ones that were irrigated from the ones that were rainfed. However, reference evapotranspiration had no significant correlation with gs but it was significant between ET₀ and both MDS and SF for both water regimens. The results of ECA did not distinguished between rainfed and irrigated plants. The closest ET₀ event to SF or MDS always triggered an empirically observed number for SF or MDS that was significatively higher than the expected coincidence if the process was purely random. Lower values of ET₀ triggered lower values of both SF and MDS and, conversely, higher values of ET₀ triggered higher values of both SF and MDS. The ECA showed that ET₀ events could not trigger simultaneously either higher or lower values for SF and MDS. A single indicator, either SF or MDS, does not reflect the grapevine response to changing environmental conditions but their combination can provide more detailed information about its water needs.

Our appreciation to Baltazar de Carvalho and to Rui Costa for their help with field work.The financial support was provided by UTAD.

We declare that there are no conflicts of interest of any kind.

1. González–Flor G, Serrano L, Gorchs G, et al. Assessment of grape yield and composition using reflectance–based indices in rainfed vineyards. Agron J. 2014;106(4):1309–1316.  
2. Conesa MR, Torres R, Domingo R, et al. Maximum daily trunk shrinkage and stem water potential reference equations for irrigation scheduling in table grapes. Agr Water Manage. 2016;172:51–61.
3. Cifre J, Bota J, Escalona JM, et al. Physiological tools for irrigation scheduling in grapevine (Vitis vinifera L.) An open gate to improve water–use efficiency? Agr Ecosys Environ. 2005;106(2–3):159–170.
4. Lebon E, Dumas V, Pieri P, et al. Modeling the seasonal dynamics of the soil water balance of vineyards. Funct Plant Biol. 2003;30(6):699–710.
5. Buckley TN. The control of stomata by water balance. New Phytol. 2005;168(2):275–292.
6. Dzikiti S, Steppe K, Lemeur R, et al. Whole–tree level water balance and its implications on stomatal oscillations in orange trees [Citrus sinensis (L.) Osbeck] under natural climatic conditions. J Exp Bot. 2007;58(7):1893–1901.
7. Fuentes S, De Bei R, Collins MJ, et.al. Night–time responses to water supply in grapevines (Vitis vinifera L.) under deficit irrigation and partial root–zone drying. Agr Water Manage. 2014;138:1–9.
8. Fernández JE, Moreno F, Martín–Palomo MJ, et al. Combining sap flow and trunk diameter measurements to assess water needs in mature olive orchards. Environ Exp Bot. 2011;72(2):330–338.
9. Ortuño MF, García–Orellana Y, Conejero W, et al. Relationships between climatic variables and sap flow, stem water potential and maximum daily trunk shrinkage in lemon trees. Plant Soil. 2006;279(1–2):229–242.
10. Zweifel R, Drew DM, Schweingruber F, et al. Xylem as the main origin of stem radius changes in Eucalyptus. Funct Plant Biol. 2014;41(5):520–535.
11. Duchesne L, Houle D. Modelling day–to–day stem diameter variation and annual growth of balsam fir (Abies balsamea (L.) Mill.) from daily climate. Forest Ecol Manag. 2011;262(5):863–872.
12. Mirás–Avalos JM, Pérez–Sarmiento F, Alcobendas R, et al. Reference values of maximum daily trunk shrinkage for irrigation scheduling in mid–late maturing peach trees. Agr Water Manage. 2016;171:31–39.
13. Macinnis–Ng C, Wyse S, Veale A, et al. Sap flow of the southern conifer, Agathis australis during wet and dry summers. Trees. 2016;30(1):19–33.
14. Allen RG, Pereira L, Raes D, et al. Crop evapotranspiration. Guidelines for computing crop water requirements. FAO Irrigation and Drainage paper No 56. Rome, Italy; 1998. p. 15–27.
15. Donges JF, Schleussner CF, Siegmund JF, et al. Event coincidence analysis for quantifying statistical interrelationships between event time series. Eur Phys J Special Topics. 2016;225(3):471–487.
16. COBA. Carta de Solos e Carta de Utilização Actual do Solo do Nordeste de Portugal. Vila Real, Portugal: Universidade de Trás os Montes e Alto Douro; 1987. p. 1–205.
17. Davis TW, Kuo CM, Liang X, et al. Sap Flow sensors: construction, quality control and comparison. Sensors. 2012;12(1):954–971.
18. Dynamax. Instructions for Calculating Sapflow; 2016.
19. Fernández JE, Cuevas MV. Irrigation scheduling from stem diameter variations: A review. Agr Forest Meteorol. 2010;150(2):135–151.
20. Siegmund JF, Tanja SGM, Ingo H, et al. Meteorological drivers of extremes in daily stem radius variations of beech, oak, and pine in northeastern germany: an event coincidence analysis. Frontiers in Plant Science. 2016.  
21. Hernandez–Santana V, Fernández JE, Rodriguez–Dominguez CM, et al. The dynamics of radial sap flux density reflects changes in stomatal conductance in response to soil and air water deficit. Agr Forest Meteorol. 2016;218–219:92–101.
22. Gartner K, Nadezhdina N, Englisch M, et al. Sap flow of birch and Norway spruce during the European heat and drought in summer 2003. For Ecol Manage. 2009;258(5):590–599.
23. Alcaras LMA, Rousseaux MC, Searles PS. Responses of several soil and plant indicators to post–harvest regulated deficit irrigation in olive trees and their potential for irrigation scheduling. Agr Water Manage. 2016;171:10–20.
24. Abdelfatah A, Aranda X, Savé R, et al. Evaluation of the response of maximum daily shrinkage in young cherry trees submitted to water stress cycles in a greenhouse. Agr Water Manage. 2013;118:150–158.
25. Tognetti R, d’Andria R, Morelli G, et al. Irrigation effects on daily and seasonal variations of trunk sap flow and leaf water relations in olive trees. Plant Soil. 2004;263(1):249–264.
26. Xu SQ, Ji XB, Jin BW. Dynamics of sap flow density in stems of typical desert shrub Calligonummongolicum and its responses to environmental variables. Ying Yong Sheng Tai Xue Bao. 2016;27(2):345–353.
27. Masmoudi CC, Masmoudi M, Jihène Abid–Karray J, et al. Sap flow measurements in young olive trees (Oleaeuropaea L.) cv. Chétoui under Tunisian conditions. Sci Hortic Amsterdam. 2011;129(4):520–527.
28. Liu C, Kang S, Li F, et al. Relationship between environmental factor and maximum daily stem shrinkage in apple tree in arid region of northwest China. Sci Hortic Amsterdam. 2011;130(1):118–125.
29. Conejero W, Ortuño MF, Mellisho CD, et al. Influence of crop load on maximum daily trunk shrinkage reference equations for irrigation scheduling of early maturing peach trees. Agr Water Manage. 2010;97(2):333–338.
30. Amani B, Olfa B, Raoul L, et al. Comparison between sap flow measurements and two prediction climate formulas to estimate transpiration in olive orchards (Oleaeuropea L. CV. Chemali). European Sci J. 2013;9(21):161–167.
31. Zhang Y, Kang S, Eric J, et al. Evapotranspiration components determined by sap flow and microlysimetry techniques of a vineyard in northwest China:Dynamics and influential factors. Agr Water Manage. 2011;98(8):1207–1214.
32. Patakasa A, Noitsakis B, Chouzouri A. Optimization of irrigation water use in grapevines using the relationship between transpiration and plant water status. Agr Ecosys Environ. 2005;106(2–3):253–259.
33. Moreno F, Fernández JE, Clothier BE, et al. Transpiration and root water uptake by olive trees. Plant Soil. 1996;184(1):85–96.
34. Intrigliolo DS, Castel JS. Evaluation of grapevine water status from trunk diameter variations. Irrig Sci. 2007;26(1):49–59.
35. Baert A, Villez K, Steppe K. Automatic drought stress detection in grapevines without using conventional threshold values. Plant Soil. 2013;369(1–2):439–452.
36. De Swaef T, Hanssens J, Cornelis A, et al. Non–destructive estimation of root pressure using sap flow, stem diameter measurements and mechanistic modelling. Ann Bot. 2013;111(2):271–282.
37. Monteiro A, Teixeira T, Lopes CM. Comparative leaf micromorphoanatomy of Vitisvinífera SSP. vinifere (Vitaceae) red cultivars. Ciencia Tec Vitiv. 2013;28(1):19–28.
38. Carvalho LC, Coito JL, Gonçalves EF, et al. Differential physiological response of the grapevine varieties Touriga Nacional and Trincadeira to combined heat, drought and light stresses. Plant Biol. 2016;18(S1):101–111.
39. Rodrigues P, Pedroso V, Gouveia JP, et al. Influence of soil water content and atmospheric conditions on leaf water potential in cv. ‘‘Touriga Nacional’’ deep–rooted vineyards. Irrig Sci. 2012;30(5):407–417.
40. De Swaef T, De Schepper V, Vandegehuchte MW, et al. Stem diameter variations as a versatile research tool in ecophysiology. Tree Physiol. 2015;35(10):1047–1061.
41. Steppe K, Lemeur R. An experimental system for analysis of the dynamic sap–flow characteristics in young trees: results of a beech tree. Funct Plant Biol. 2004;31(1):83–92.