The paper unveils zero velocity curves of a dust grain particle around eleven equilibrium points under effects of radiation, perturbations and variable Kruger 60. The study is carried out using the model formulations of the restricted three-body problem in which the primaries are assumed to be radiation sources and vary their masses with time coupled with small perturbations in the Coriolis and centrifugal forces due to circular motion. The equations of motion of the non-autonomous system and those of the autonomized equations with constant coefficients have been stated and the equilibrium points explored.  Numerical illustrations have been provided to support the study for a particular case when the dust grain moves under the influence of the central binary Kruger 60. It is seen that there exist a pair of triangular points, five collinear equilibrium points, and four out-of-plane equilibrium points, which are defined by the radiation pressure of the Kruger 60, centrifugal perturbation and the arbitrary constant $K$  which defines the sum of the masses of Kruger 60. Finally, the zero velocity curves of the dust grain around the equilibrium points are explored and the effects of the parameters divulged. In the case of the collinear equilibrium points, as $K$  increases the region where motion is allowed decreases, while in the case of the triangular points, the dust grain is permitted to move around the primaries and the triangular points and is also allowed access to the exterior realm as $K$  increases. In the case of the out-of-plane equilibrium points, as $K$  increases the region where motion is allowed decreases while the presence of the perturbing forces due to radiation and centrifugal perturbation also reduces the region where motion of the dust grain particle is allowed. It is seen that the Coriolis perturbation do not affect the locations and zero velocity curves around all the equilibrium points.

Keywords: Kruger 60, radiation pressure, perturbations, variable masses, zero velocity curves

The restricted three-body problem (R3BP) illustrates the motion of an infinitesimal mass moving under the gravitational effects of two finite masses, called primaries, which move in circular orbits around their center of mass on account of their mutual attraction and the infinitesimal mass not influencing the motion of the primaries. The R3BP is still a stimulating and active research field that has been receiving considerable attention of scientists and astronomers because of its applications in dynamics of the solar and stellar systems, lunar theory, and artificial satellites.

Numerous examples of the restricted problem are available in space dynamics. One of them is the classical three-body problem viz; the Sun-Earth-Moon combination and describing the motion of the moon. The motion of a Trojan asteroid attracted by the Sun and Jupiter is another example. One of the foremost in space science is the creation of artificial bodies, which are required to move in the neighborhood of two natural celestial bodies, which is also similar to the restricted problem.

Some investigations of the R3BP have considered the case where the masses of the bodies are constant under different classifications.¹⁻⁷ Other studies have taken into account mass variations in the model of the R3BP.⁸⁻¹¹ The classical R3BP did not incorporate into its model the case when one or both the primaries are a source of radiation. This formulation according to Radzievskii¹² is called the photogravitational problem, which he applied to the Sun-Planet-Particle and Galaxy Kernel-Sun-Particle systems. Radiation pressure act as an orbital perturbations and affects the orbits and trajectories of small bodies, all space crafts and all natural bodies (comets, asteroids, dust grains, gas molecules). It can cause dust grains to either leave the Solar system or spiral into the Sun. Because of the many importance of radiation pressure, several researchers have included radiation pressure force of either one or both primaries in the study of the R3BP. They include among others, AbdulRaheem and Singh (2006),⁴ Singh and Leke (2010, 2014),^6,13 and Singh & Haruna.⁵

In the formulation of the classical R3BP, the third body of infinitesimal mass is considered to move, only under the mutual gravitational force of the primaries, but in practice, Coriolis and centrifugal forces are effective and small perturbations affect these forces. Examples include: small deviation of disc stars on circular orbits and motion of a close artificial satellite of the Earth perturbed by the atmospheric friction and the shape of the Earth. Hence, it is reasonable and permissible to include these forces in the study of the R3BP. Several interesting studies when Coriolis and centrifugal forces are slightly perturbed have been carried out by Bhatnagar & Hallan,³ AbdulRaheem & Singh,⁴ Singh & Leke¹⁴ and Singh & Haruna.⁵

Zero velocity surfaces are important because they form the boundary of regions from which the dust grain is dynamically excluded. Luk’yanov¹⁵ examined zero velocity surfaces in the restricted three-body problem with variable masses and since then, not much further studies have been carried out. Motivated by this, our interest is to explore zero velocity curves of a dust grain particle around the equilibrium points when the dust grain particle moves in the gravitational field of the binary Kruger 60 whose masses vary and are emitters of radiation pressure under small perturbations in the Coriolis and centrifugal forces.

The overview of the paper is as follows: The dynamical framework is given in Sect. 2 and the equilibrium points are given in Sect 3. The results and discussion are given in section 4. Here, numerical estimations of the locations of the triangular, collinear and out-of-plane points equilibrium points and the zero velocity curves around them, are explored. Section 5 concludes the paper.

Dynamical equations

Following the methodology deployed in the paper Singh et al.,¹³ the equations of motion of R3BP with variable masses when both primaries are luminous bodies under effect of small perturbation in the Coriolis and centrifugal forces, have the form

$\ddot{x}-2\phi \omega \dot{y}={\omega }^{2}x\psi +\dot{\omega }\phi y-\frac{{\mu }_1{q}_1(x-x_1)}{r_1^3}-\frac{{\mu }_2{q}_2(x-x_2)}{r_2^3}$   

$\ddot{y}+2\phi \omega \dot{x}={\omega }^{2}y\psi -\dot{\omega }\phi x-\frac{{\mu }_1{q}_{1}y}{r_1^3}-\frac{{\mu }_2{q}_{2}y}{r_2^3}$   (1)

$\ddot{z}=\frac{{\mu }_1{q}_{1}z}{r_1^3}-\frac{{\mu }_2{q}_{2}z}{r_2^3}$   

where $q_1{q}_2$  are the radiation factors of the bigger and smaller primaries respectively and are such that $q_i=1-\frac{F{p}_i}{F{g}_i}$ , $\varphi$  and $\psi$  are the perturbation in the Coriolis and centrifugal forces respectively, the unperturbed value is unity.

The equations of motion (1) are non-autonomous differential equations. Thus, following Singh et. Al.,¹³ the autonomized equations with constant coefficients:

$\xi "-2\phi \eta \text{'}=\frac{\partial \Omega }{\partial \xi },$ $\eta "+2\phi \xi \text{'}=\frac{\partial \Omega }{\partial \eta },$ $\zeta "=\frac{\partial \Omega }{\partial \zeta }$   (2)

where  $\Omega =\frac{\left(\psi +K-1\right)\left({\xi }^2+{\eta }^2\right)}{2}+\frac{\left(K-1\right){\zeta }^2}{2}+\frac{q_{1}K(1-\upsilon )}{{\rho }_1}+\frac{q_{1}K\upsilon }{{\rho }_2}$

${\rho }_1=\sqrt{{\left(\xi +\upsilon \right)}^2+}{\eta }^2+{\zeta }^2,$ ${\rho }_2=\sqrt{{\left(\xi +\upsilon -1\right)}^2+}{\eta }^2+{\zeta }^2$   

where $\upsilon =\frac{m_2}{m_1+m_2}$ is the mass parameter and $K$ is a constant of a particular integral of the GMP which defines the sum of the masses of the primaries.

Equations (2) admits the Jacobi integral

$2\Omega (\xi ,\eta ,\zeta )-(\xi {\text{'}}^2,\eta {\text{'}}^2,\zeta {\text{'}}^2)=C$   (3)

where C is the Jacobi constant.

Locations of equilibrium points

The solutions of the autonomized system are sought by finding the particular solutions or the libration or equilibrium points. These are found by equating the right hand side of the equations of system (2) to zero. That is

${\omega }_0^2\left(\psi +K-1\right)\xi -q_1\frac{K(1-\upsilon )}{{\rho }_{{}_1}^3}\left(\xi +\upsilon \right)-q_2\frac{K\upsilon }{{\rho }_{{}_2}^3}\left(\xi +\upsilon -1\right)=0$   

$\left[{\omega }_0^2\left(\psi +K-1\right)-q_1\frac{K(1-\upsilon )}{{\rho }_{{}_1}^3}-q_2\frac{K\upsilon }{{\rho }_{{}_2}^3}=0\right],\eta =0,$   (4)

$\left[\left(K-1\right){\omega }_0^2-q_1\frac{K(1-\upsilon )}{{\rho }_{{}_1}^3}-q_2\frac{K\upsilon }{{\rho }_{{}_2}^3}\right]\zeta =0$   

Triangular points

The triangular points are the solutions of the first two equations of system (4). Solving them using perturbation method, we get

$\xi =\frac{1}{2}-\upsilon +\frac{K^{\frac{2}{3}}}{{\left(\psi +K-1\right)}^{\frac{2}{3}}}\left[\frac{1}{3}\left(1-q_2\right)-\frac{1}{3}\left(1-q_1\right)\right]$   (5)

$\eta =\pm \frac{\sqrt{4K^{\frac{2}{3}}-{\left(\psi +K-1\right)}^{\frac{2}{3}}}}{2{\left(\psi +K-1\right)}^{\frac{1}{3}}}{\left\{1-\frac{2K^{\frac{2}{3}}}{4K^{\frac{2}{3}}-{\left(\psi +K-1\right)}^{\frac{2}{3}}}\left[\frac{1}{3}\left(1-q_1\right)-\frac{1}{3}\left(1-q_2\right)\right]\right\}}^{\frac{1}{2}}$   

These points are denoted by $L_4$ and $L_3$  respectively, and differs from that in Singh et. Al.,¹³ only due to the radiation pressure of the second primary. Hence, the triangular points of Singh et. Al.,,¹³Singh & Leke,¹⁴ Luk’yanov⁹ and Bekov⁸ can all be recovered from equations (5).

Locations of collinear points

The collinear points are the solutions of the first equation of (4). Solving, we get the following three polynomials of degree five, each of which corresponds to the collinear points:

$\psi {\epsilon }_1^5+(2-\upsilon )\psi {\epsilon }_1^4+(1+2\upsilon )\psi {\epsilon }_1^3-(q_2\upsilon -\upsilon \psi +q_1-q_1\upsilon ){\epsilon }_1^2-2q_1(1-\upsilon ){\epsilon }_1-q_1(1-\upsilon )=0$   

$\psi {\epsilon }_2^5+(3-\upsilon )\psi {\epsilon }_2^4+(3+2\upsilon )\psi {\epsilon }_2^3-(\psi -\upsilon \psi +q_2\upsilon -q_1+q_1\upsilon ){\epsilon }_2^2-2q_2\upsilon {\epsilon }_2-q_2\upsilon =0$   (6)

$\psi {\epsilon }_3^5+(3+\upsilon )\psi {\epsilon }_3^4+(3-2\upsilon )\psi {\epsilon }_3^3-(\psi -\upsilon \psi -q_2\upsilon -q_1+q_1\upsilon ){\epsilon }_3^2-2q_2\upsilon {\epsilon }_3-q_2\upsilon =0$   

Equations (6) are equations of degree five in $\epsilon {}_i(i=1,2,3)$ , and positions of the collinear point $L_i(i=1,2,3)$  are respectively

${\xi }^1=-\upsilon -\epsilon {}_1$ , ${\xi }^2=1-\upsilon -\epsilon {}_2$ , ${\xi }^3=1-\upsilon +\xi {}_3$ ,  (7)

Location of out-of-plane points

 The out of plane EPs are located outside the plane of motion and are found by solving the first and third equation of (4), using the Newton-Raphson method, to get

$\xi =\frac{1}{2}\upsilon (1-\upsilon )(K-1)\frac{3{(K-1)}^{\frac{2}{3}}(1-2\upsilon )-2K^{\frac{2}{3}}\left(1-q_1\right)+2K^{\frac{2}{3}}\left(1-q_2\right)}{3\upsilon (1-\upsilon ){(K-1)}^{\frac{5}{3}}+\psi K^{\frac{2}{3}}\left[1-\frac{2}{3}\upsilon \left(1-q_1\right)-\frac{2}{3}(1-\upsilon )\left(1-q_2\right)\right]}$   

$\zeta \pm \sqrt{{\left\{\frac{K\upsilon }{-\psi \xi +\upsilon (K-1)}\right\}}^{\frac{2}{3}}\left[1-\frac{2}{3}\left(1-q_2\right)\right]-{\left(\xi +\upsilon -1\right)}^2}$   (8)

and

$\xi =\frac{1}{2}\upsilon (1-\upsilon )(K-1)\left[\frac{3{(K-1)}^{\frac{2}{3}}(1-2\upsilon )-2K^{\frac{2}{3}}\left(1-q_1\right)+2K^{\frac{2}{3}}\left(1-q_2\right)}{3\upsilon (1-\upsilon ){(K-1)}^{\frac{5}{3}}+\psi K^{\frac{2}{3}}\left[1-\frac{2}{3}\upsilon \left(1-q_1\right)-\frac{2}{3}(1-\upsilon )\left(1-q_2\right)\right]}\right]$   

$\zeta \pm \sqrt{{\left\{\frac{K\left(1-\upsilon \right)}{\psi \xi +\left(1-\upsilon \right)(K-1)}\right\}}^{\frac{2}{3}}\left[1-\frac{2}{3}\left(1-q_1\right)\right]-{\left(\xi +\upsilon \right)}^2}$   (9)

where $-\psi \xi +\upsilon (K-1)>0$ , $\psi \xi +(K-1)\left(1-\upsilon \right)>0$ , $(K-1)>0$ ; and $\left(1-q_i\right)<<1(i=1,2)$ . The coordinate (8) is denoted by $L_{6,7}$ , while the coordinate (9) is denoted by $L_{8,9}$ . Other previous works, such as Singh & Leke,¹⁰ Luk’yanov⁹ and Bekov⁸ can be confirmed from our results. When $K=1$ , the points do not exist, instead an infinite line of EPs denoted by $L_{\pm \infty }$ exist on the $\zeta -$ plane and referred to as infinitely remote solutions.

Next, we focus on the numerical applications of the study, by first numerically evaluating the positions of the equilibrium points for the binary system Kruger 60. We adopt the numerical data used in Singh & Simon.¹⁶ For the mass parameters, we take $\upsilon =0.3937$ for Kruger 60 while for the radiation pressure of the primaries we take $q_1=0.99992$ , $q_2=0.99996$ . Further, following Singh & Leke,¹⁴ we take $\psi =1.002$ and $\phi =1.003$ . All numerical and graphical explorations have been carried out using the software Mathematica.¹⁷

Triangular equilibrium points

First, we compute numerically the locations of the triangular points given in equations (5) in Table 1. It is observed that the radiation pressure of both binaries causes a slight deviation. The graphs of the triangular points for the binaries Kruger 60 are given in Figure 1a-e.

We have numerically explored the locations of the triangular equilibrium points in Table 1 when the dust grain particle moves under the gravitational influence of a binary Kruger 60. The Table 1 gives the positions of the dust grain particle when motion takes place in the $\xi \eta -$ plane and these points have been analytically obtained in equations (5). The 2^nd and 3^rd column are the positions of the triangular points when there is no perturbing force present (classical case) while the last two columns are the locations of the triangular points under the combined effects of radiation of both primaries, centrifugal perturbation and the mass variation constant, kappa. It is seen that, in the absence of the centrifugal force, the parameter kappa does not appear in the locations given in equations (5). From the Table 1, it is seen that when $0<K\le 0.00001$ , the triangular points do not exists but exists when $0.001\le K<\infty$ . Also for $500\le K<\infty$  the points are same for values of kappa in this interval.

The graphs of the triangular points for different values of the parameter kappa when the test particle moves under the photogravitational effects of the binary Kruger 60 have been presented in Figure 1a-e.

Figure 1a-e give the locations of the triangular equilibrium points under combined effects of radiation, perturbation and mass variations. The graphs have been obtained from the numerical values given in Table 1 and have been plotted for different values of the parameter kappa. Figure 1a gives the locations of triangular EP for Kruger 60 when $K=0.001$ while Figure 1b is the case when $K=0.01$ . The combined plot of both Figure 1a and 1b is given in Figure 1c to show the shift in the positions of the triangular points. Figure 1d is the plot of the triangular points when kappa is approaching infinity. Finally, the combined plots of Figure 1a, 1b and 1d have been given in Figure 1e. Clearly, it is seen that has kappa increases the locations of the triangular points drifts away from the primaries.

Figure 1 Locations of Triangular EP for Kruger 60 when (a)K=0.001 (b) K=0.01 (c)K=0.01 Combined plot of a and b (d) K→∞ (e) combined plot of a, b and d.

Next, we give the zero velocity surfaces of the triangular equilibrium points $L_{4,5}$  in Figure 2 to Figure 4.

Zero velocity curves

The Jacobi integral is given in equation (3). For a given value of C, we can obtain the zero-velocity curves around the equilibrium points of the circular R3BP with variable masses on the in-plane and out-of-plane equilibrium points using equation (3). Zero velocity surfaces are important because they form the boundary of regions from which the dust grain is dynamically excluded. The regions from which motion of the dust grain particle is forbidden grow in area as the energy constant increases, and vice versa. For a given value of C, we can obtain the zero-velocity surfaces of the circular R3BP on the $\xi \eta -$  plane and $\xi \zeta -$  plane as shown in Figures 2 to Figures 4, Figure 7 to 9 and Figure 11 to Figure 12, respectively. These Figures illustrate for different value of the energy constant how the region from which the dust grain particle is dynamically excluded-which we shall term forbidden region and evolves as the value of the energy constant under radiation pressure of both primaries, centrifugal perturbation and mass variation constant kappa, are varied. Any point not in the forbidden region is in the so called permissible or allowed region.

Now, we plot the zero velocity curves of a dust grain particle around triangular equilibrium points given in Table 1, in Figures 2 to 4 for different values of the parameter $K$  in the presence or absence of the perturbing forces due to radiation and small perturbations in the Coriolis and centrifugal forces.

Figure 2-4 describes the ZVC of the dust grain around triangular points. The blue region depicts regions where motion of the dust grain is prohibited, while the red region are regions where motion is permitted. From Figure 2, it is seen that the energy constant is so small and yet motion of the dust grain is not allowed anywhere inside the plane of motion around the triangular points. In Figure 3, it is observed that the dust grain is permitted to move around the primaries and around the triangular points, but is restricted from moving to the exterior realm. In Figure 4, the dust grain is permitted to move around the primaries and the triangular points, and free to travel to the exterior realm.

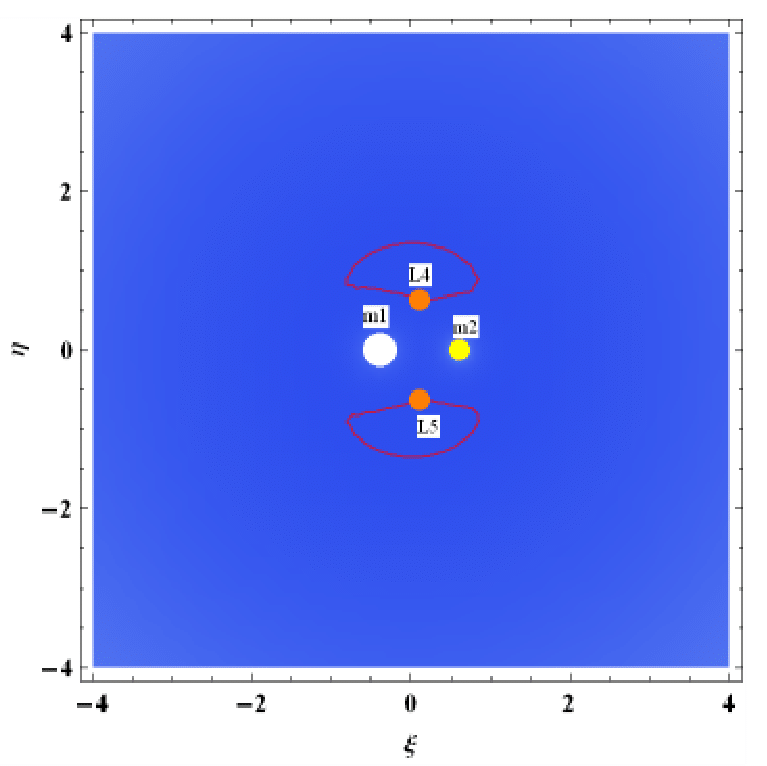
Figure 2 Zero Velocity Curves of Triangular Point L_4,5 for Kruger 60 when C=0.00744687, q₁=10.99992, q₂=0.99996, ψ=1.002 and K=0.001.

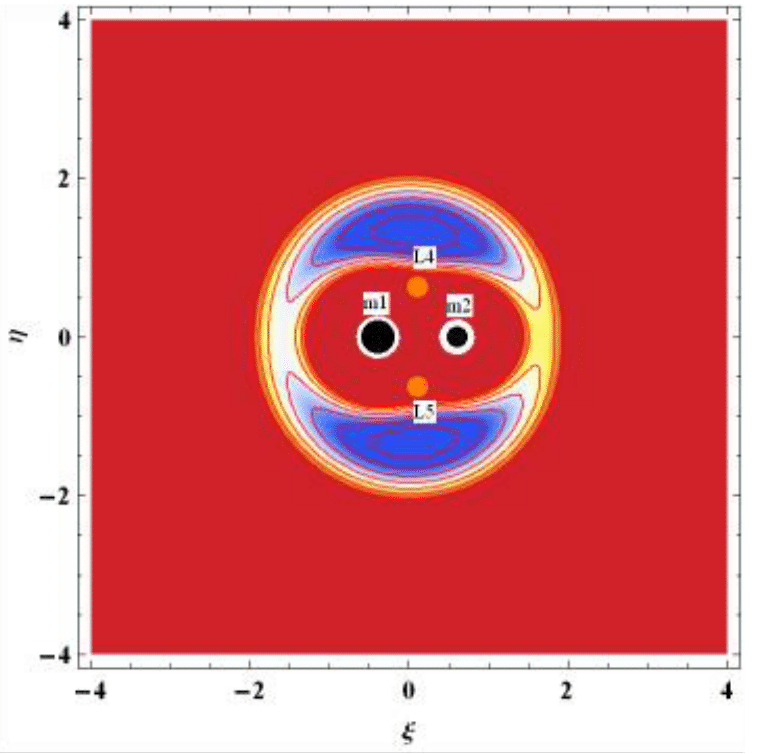
Figure 3 Zero Velocity Curves of Triangular Point L_4,5 for Kruger 60 when C=4.09464, q₁=q₂=ψ=K=1.

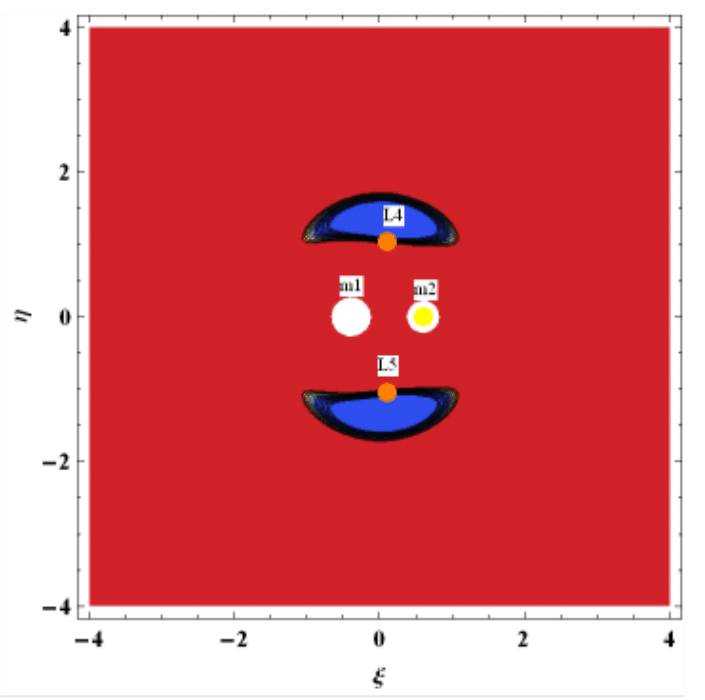
Figure 4 Zero Velocity Curves of Triangular Point L_4,5 for Kruger 60 when C=40.9493, q₁=0.99992, q₁=0.99996, ψ=1.002 and K=10.

Collinear equilibrium points

Next, we compute in Table 2 the coordinates of the collinear equilibrium points $L_1$ , $L_2$  and $L_3$ , respectively. These are the roots of the equations (6), respectively, for Kruger 60 when $\psi =1.002$  and $0<K<\infty$ . We numerically explore the roots ${\epsilon }_i(i=1,2,3)$  of the three polynomials (6) for $q_1=0.99992$ ,  $q_2=0.99996$ , $\psi =1.002$  and substitute each in the respective equation in equations (7).

We compute these points and it is seen that when one or both primaries are radiation emitters, there are five points with two additional collinear points $L_{31}$ ,and $L_{32}$ . The collinear points $L_1$ and $L_{31}$ lie to the left of the bigger primary while $L_2$ and $L_{32}$ lie between the primaries and the points $L_3$ lie to the right of the smaller primary, as shown in Figures 5 and 6.

Figure 5a is the location of the dust grain particle on the line joining the primaries when there are no perturbing forces due to the radiation of the primaries and small perturbation in the centrifugal forces. It is observed that there are only three points with the first collinear points lying to the left of the bigger primary while the second point is positioned between the primaries and the third point lies on the right of the smaller primaries. Figure 5 b give the locations of the collinear equilibrium points for Kruger 60 when both primaries are a radiating sources and under combined effects of perturbation and mass variation.  The point $L_1$  (Red) lies to the left of the bigger primary. The point $L_2$  (Green) is located between the primaries while the points $L_{31}$  (Yellow) lies to the left of the bigger primary and $L_{32}$  (Black) lies between the primaries and the point $L_3$ (Blue)is located on the right of the smaller primary. In this case additional two collinear points $L_{31}$ and $L_{32}$  exists when one or both primaries are radiation emitters or when centrifugal perturbation is present. The variations in the location of the collinear point $L_2$ when the classical case evolves into the combined effects of radiation, perturbation and mass variation has been shown in Figure 6. The blue spot designates the collinear point in the absence of any perturbing force due to radiation, perturbation or mass variation while the red spots signifies the effects of the combined perturbing forces on location of collinear equilibrium points $L_2$ . These result is different from those of Szebehely,² Bekov,⁸ Luk’yanov^9,15 and Singh & Leke.¹⁰

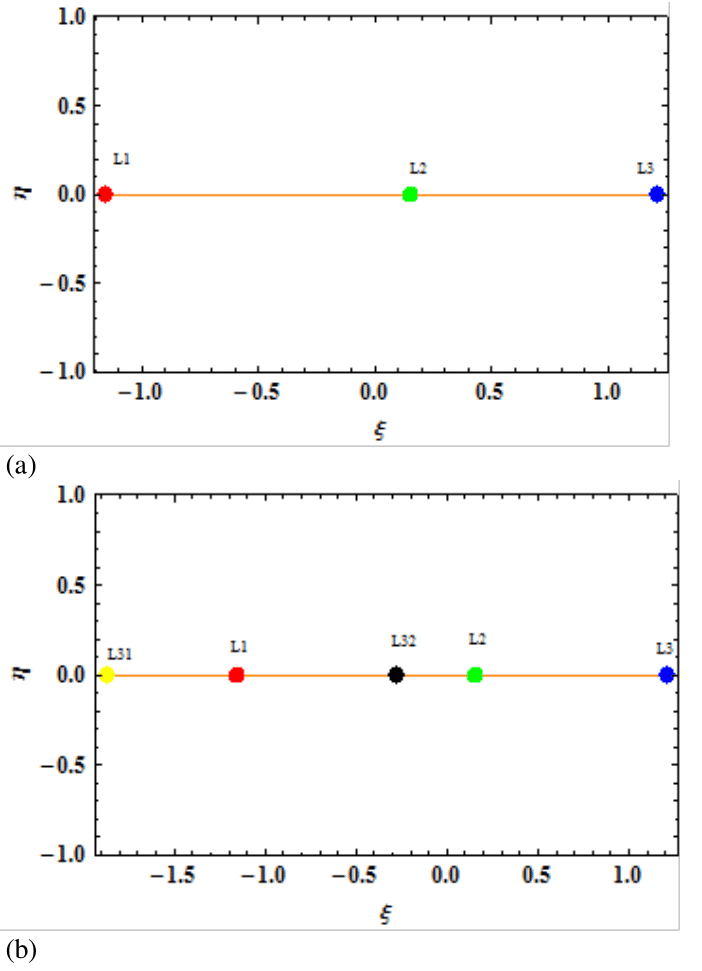
Figure 5 Collinear equilibrium points L₁ (Red), L₂ (Green), and L₃ (Blue) of the R3BP when υ=0.3937 and (a) Classical case (b) combined effects.

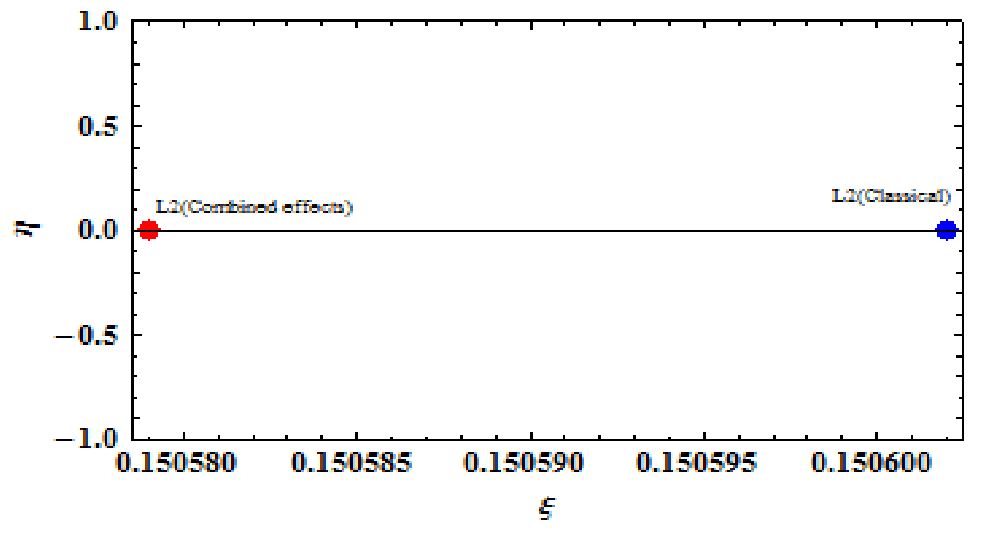
Figure 6 Effects of the combined perturbing forces on location of collinear equilibrium points L₂.

Zero velocity curves

We shall discuss the zero velocity curves around the collinear points $L_1$ ,$L_2$ ,$L_3$ , and the two additional points $L_{31}$ and $L_{32}$ . We shall unveil where motion of the infinitesimal mass is dynamically forbidden or permissible. In Figures 7 to Figure 9.

Figure 7 to Figure 9 show the zero velocity curves of collinear points. Figure 7 gives the ZVC for the classical R3BP when the binary is not a radiating one and small perturbation with mass variation neglected. Here, the region where motion of the test particle is allowed is much more than the case given in Figure 8. Also, the dust grain is permitted to move around the equilibrium points but is restricted from travelling to the exterior region of motion. In both Figure 8&9, motion of the infinitesimal is not permitted around $L_{31}$ and the exterior realm.

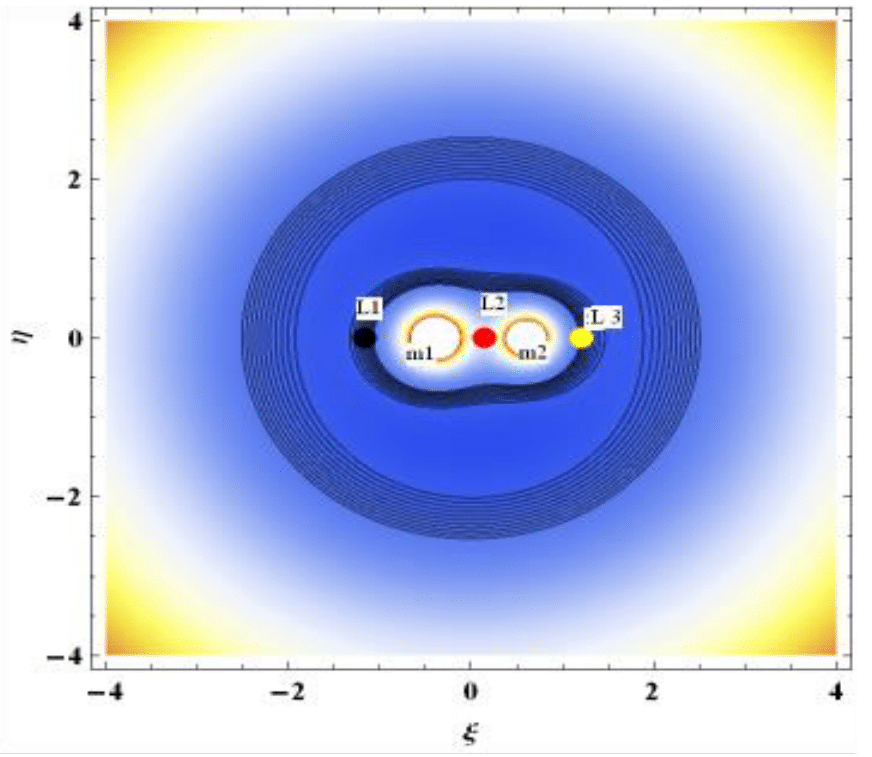
Figure 7 Zero velocity curves of collinear pointsL_1,2,3 for Kruger 60 when K=1, C=5.9835 and both primaries are non-radiating.

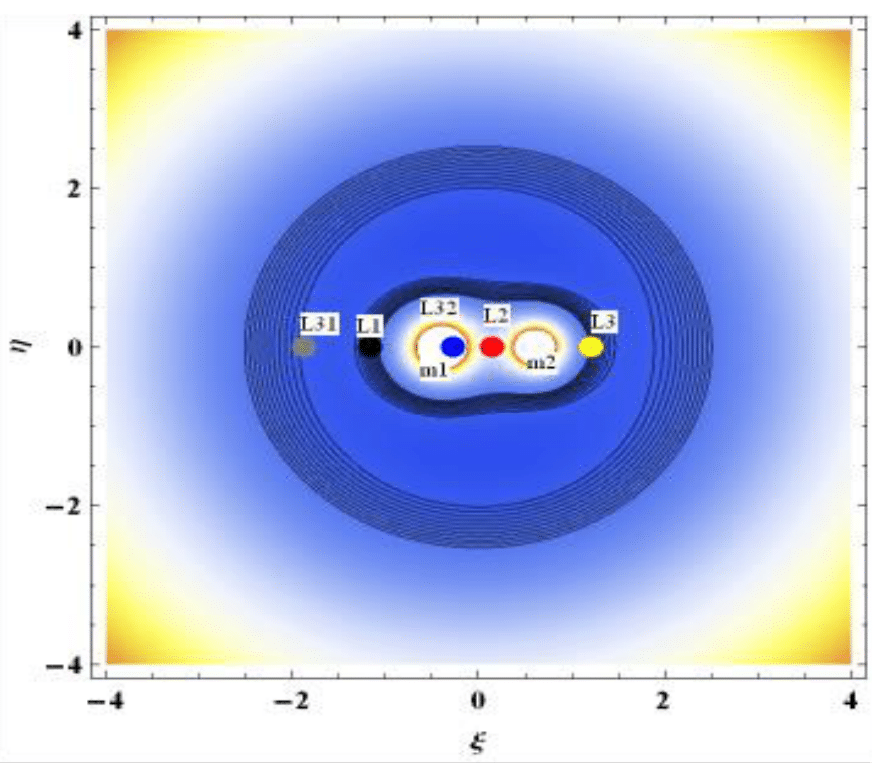
Figure 8 Zero velocity curves of collinear points for Kruger 60 when K=1, C=5.99157, ψ=1.002 and both primaries are non-radiating.

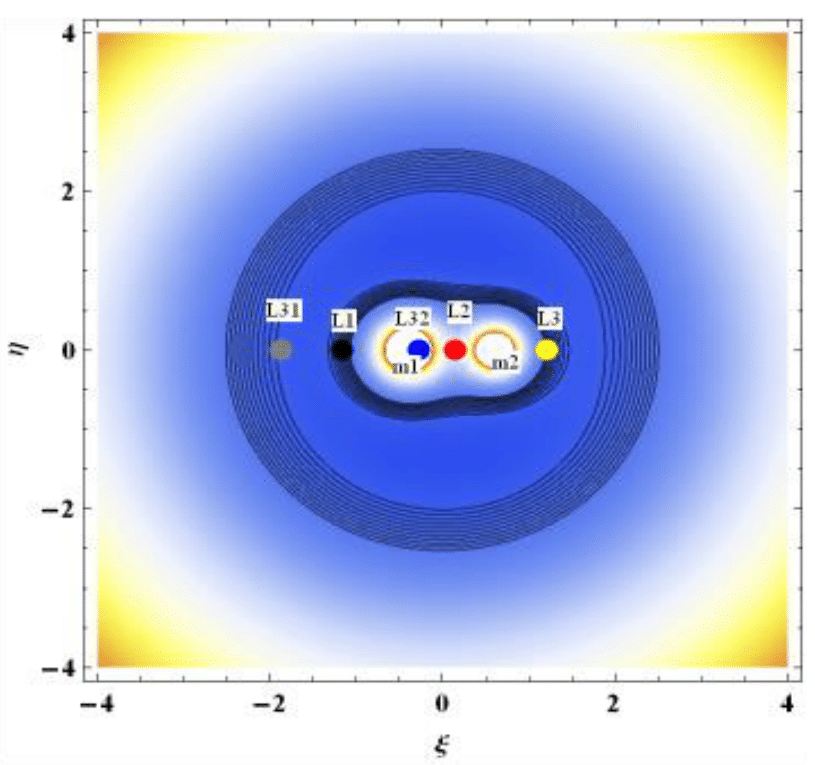
Figure 9 Zero velocity curves of collinear points for Kruger 60 when k=1, C=5.99149, ψ=1.002 and q₁=0.99992, q₂=0.99996.

Out-of-plane equilibrium points

Equations (8) and (9) give the coordinates of two pair of out-of-plane equilibrium points $L_{6,7}$ and $L_{8,9}$ . These points exists only for $K>1$  provided $\upsilon (K-1)>\psi \xi$  and $(K-1)(1-\upsilon )+\psi \xi >0$ , respectively and depends on the mass parameter, radiation pressure of the primaries, the centrifugal perturbation and the mass variations constant (kappa). The coordinate (8) is denoted by $L_{6,7}$ , while the coordinate (9) is denoted by $L_{8,9}$ . In Table 3 , we compute numerically,  the coordinates of the out-of-plane equilibrium points $L_{6,7}$ and $L_{8,9}$  when $1-K<\infty$  for the binary Kruger 60 when  the perturbing forces due to radiation of the primaries and the centrifugal perturbation are absent (The classical case) and when they are present (Combined effects, which we have denoted by C and CE, respectively. 

It is seen from Table 3, that the positions deviate from the case when no perturbing force is present. In particular, it is seen that the points $L_{6,7}$ are located nearer the origin of the masses than the points described by $L_{8,9}$ . As the parameter kappa increases and approaches infinity, the points $L_{6,7}$  and $L_{8,9}$  coincide under the combined effects of radiation and perturbation.  The out-of-plane points $L_{6,7}$  and $L_{8,9}$  of the dust grain particle in the vicinity of the binary Kruger 60, are given in Figures 10.

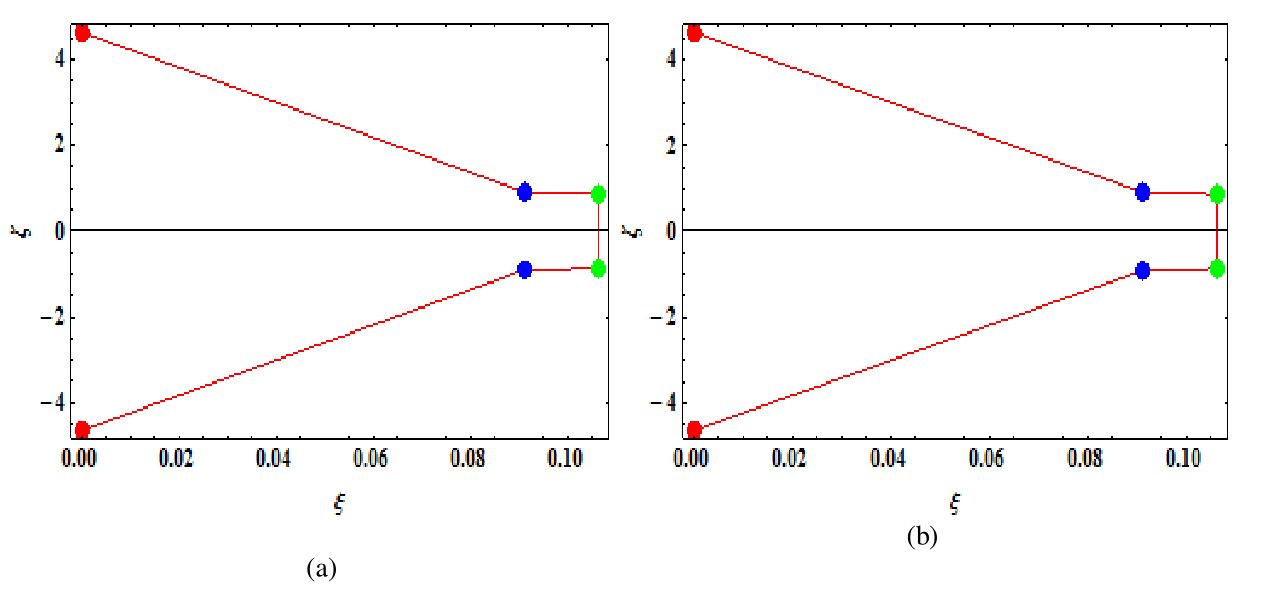
Figure 10 Out-of-plane Equilibrium Points around Kruger 60 under combined effects of radiation and perturbation for K=1.01 (Red), K=10 (Blue) and K→∞ (Green) for (a) L_6,7 and (b) L_8,9 .

Zero velocity curves   

Figure 11 gives the ZVC of the dust grain particle around the out-of-plane equilibrium points under combined effects of radiation and perturbation in the centrifugal force for different value of the parameter $K=1.01$ when the binary is Kruger 60. From Figure 11a, it is seen that the region where motion of the dust grain particle is permissible is large. However, motion around the out-of-plane points is not possible since the points lie in the regions where motion is forbidden, but can travel to the exterior region. Figure 11b is the case when the parameter $K$  increases to 10 and it is seen that the energy constant increases and the region where motion of the dust grain particle is allowed decreases. In this case, the dust grain is permitted to move around the primaries and the out-of-plane points, and also can travel to the exterior region. Figure 11c and 11d are the ZVC when $K$  is 1000 and when it is approaching infinity, respectively. The energy constant $C$ increases tremendously and the region when motion is allowed are around the primaries and the out-of-plane equilibrium points but cannot move to the exterior realm.

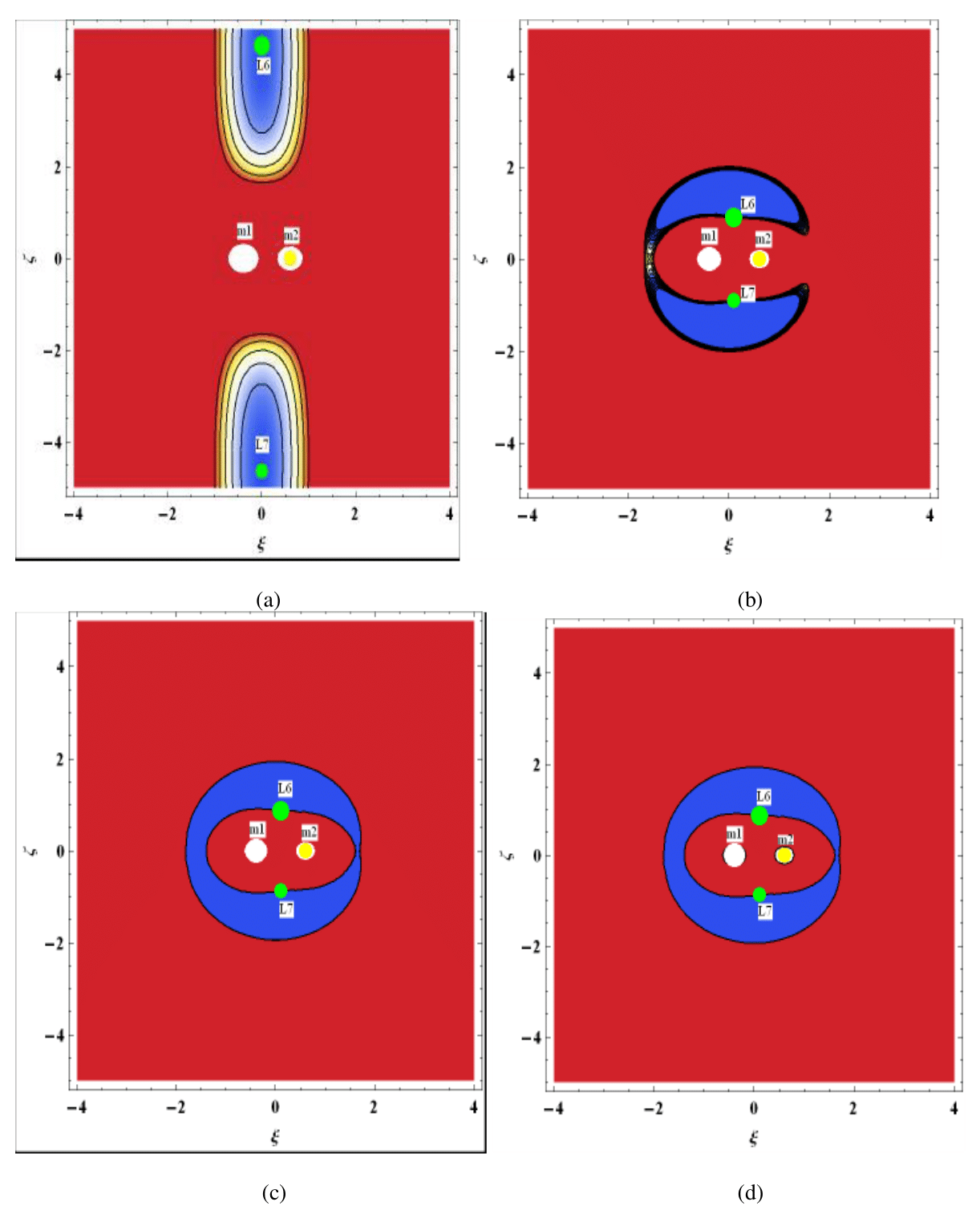
Figure 11 Zero Velocity Curves of Out-of-plane Points for Kruger 60, for $q_1=0.99992$ , $q_2=0.99996$ ,$\psi =1.002$ when (a)$\kappa =1.01$ and $C=0.400763$ (b) $K=10$ and $C=44.922$ (c) $K=1000$ and $C=4762.49$ (d) $K\to \infty$ and $C\to \infty$ .

Figure 12a-d are the zero velocity curves of the dust grain particle around the out-of-plane equilibrium points when the radiation and centrifugal perturbation are absent. In this case, the energy constant  decreases a bit from that in Figure 11a-d (when combined effects of the perturbing forces are present). Hence, the region where motion of the dust grain particle is dynamically permissible increases in the absence of the perturbing forces. Also, the out-of-plane points are no travel zone for the dust grain particle, in Figure 11a and Figure 12a, while motion around the out-of-plane equilibrium points is possible when $K=10$  (Figure 11b and Figure12b) in the presence of absence of the perturbing forces due to radiation and the centrifugal perturbation. Therefore, we can conclude that increase in the parameter $K$  reduces the region where motion of the dust grain is allowed while the effects of the forces of radiation and centrifugal perturbation produce a decrease in the region where motion of the dust grain particle is allowed. Our results are similar to those of Luk’yanov¹⁵ and Szebehely¹ when both primaries are non-radiating bodies and motion on circular orbits are not perturbed by small perturbations in the Coriolis and centrifugal forces.

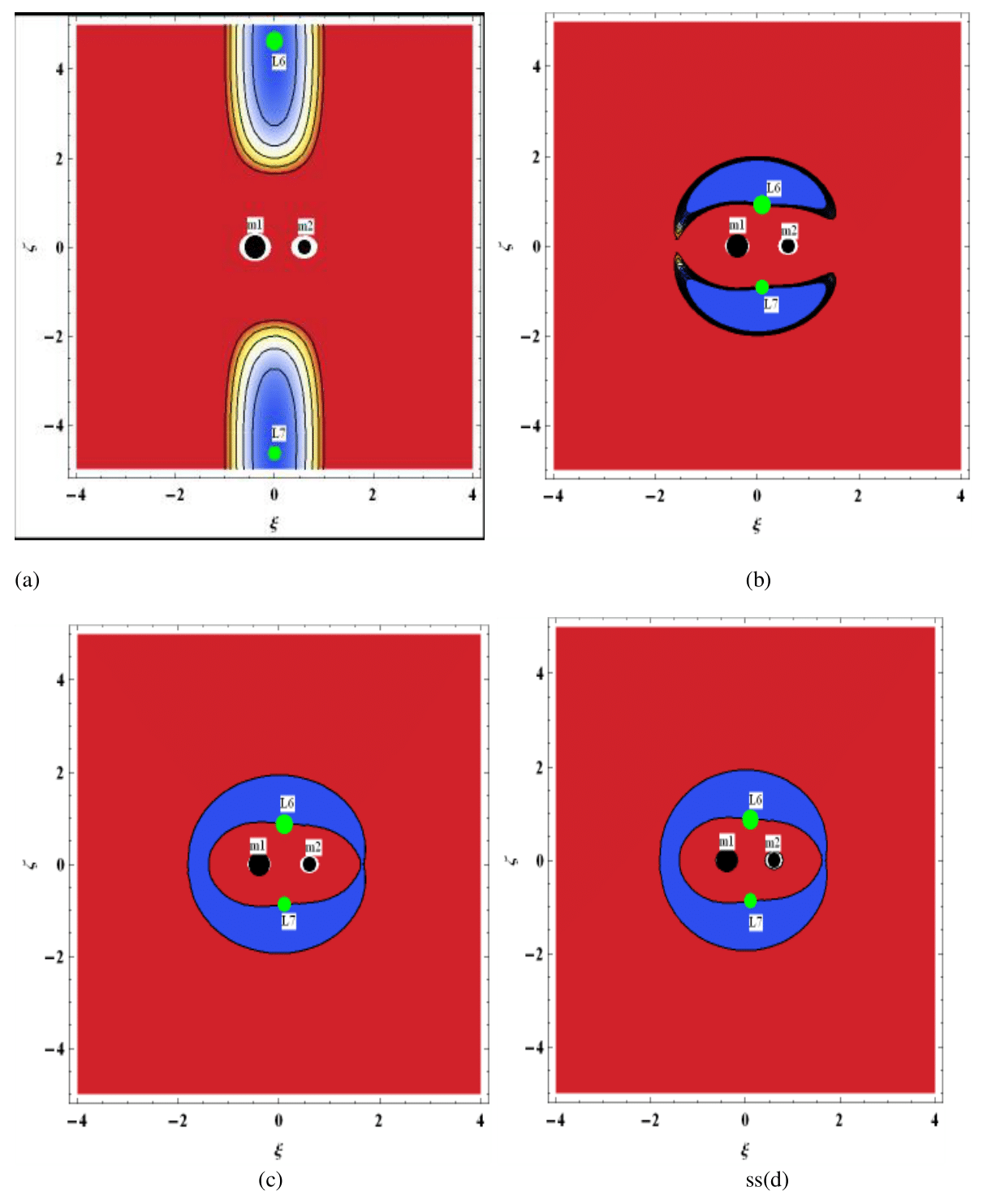
Figure 12 Zero Velocity Curves of Out-of-plane Points for Kruger 60 for $q_1=q_2=1$ , $\psi =1$ when (a) $K=0.01$ and $C=0.400776$ (b)$K=10$ and $C=44.4197$ (c) $K=1000$ and $C=4758.13$ (d) $K\to \infty$ and $C\to \infty$ .

The paper explored zero velocity curves of a dust grain particle around the equilibrium points under effects of radiation, perturbation and mass variations of the binary Kruger 60. The primaries are assumed to be emitters of radiation pressure and undergo mass variation in accordance with unified Mestschersky Law¹⁸ while their motion is defined by the Gylden-Mestschersky problem.^19,20 Due to motion on circular orbit small perturbations in the Coriolis and centrifugal forces are assumed to be effective. The equations of motion of the time dependent and those with constant coefficients were deduced and the solutions explored. There exist a pair of triangular points, five collinear equilibrium points (numerically) and four out-of-plane equilibrium points, all of which depends on the radiation pressure, perturbation in the centrifugal force and the parameter which represents variations in sum of the masses of the primaries. Numerical illustrations were provided for a particular case in which the dust grain particle moves under the influence of the central binary Kruger 60. The zero velocity curves around the equilibrium points were explored and the effects of the parameters divulged. In the case of the collinear equilibrium points, the energy constant increases as $K$  increases and consequently the region where motion is allowed decreases, while in the case of the triangular points it is seen that the energy constant is so large and consequently region where motion of the test particle is allowed is only the orbits about the triangular points. If the test particle leaves orbit, then it is likely to escape into space. In the case of the out-of-plane equilibrium points, the energy constant increases as $K$  increases and consequently the region where motion is allowed decreases while the presence of the perturbing forces due to radiation and centrifugal perturbation also reduces the region where motion of the dust grain particle is allowed. The Coriolis perturbation do not affect the locations and ZVC around all the equilibrium points.

Our results are similar to those of Luk’yanov¹⁵ and Szebehely¹ when both primaries are non-radiating bodies and motion on circular orbits are not perturbed by small perturbations in the Coriolis and centrifugal forces. The forward projections of the problem are quite numerous. These includes, the consideration of a circumbinary disc around the primaries, which is our current area of research interest.

None.

The authors declare that there is no conflict of interest.

1. Szebehely VG. Theory of Orbits. Academic press, New York; 1967.
2. Radzievskii VV. Astron.Zh (USSR). 1953;30:265.
3. Bhatnagar KB, Hallan PP. The effect of perturbations in Coriolis and centrifugal forces on the linear stability of equilibrium points in the restricted problem of three bodies. Celest Mech. 1983;30:97−114.
4. AbdulRaheem A, Singh J. Combined effects of perturbations, radiation and oblateness on the stability of equilibrium points in the restricted three-body problem. Astronomical Journal. 2006;131:1880−1885.
5. Singh J, Haruna S. Periodic orbits around triangular points in the restricted problem of three oblate bodies. American Journal of Astronomy and Astrophysics. 2014;2(2):22−26
6. Singh J, Leke O. Analytic and numerical treatment of motion of dust grain particle around triangular equilibrium points with post-AGB binary star and disc. Advances in Space Research. 2014;54:1659–1677.
7. Alrebdi HI, Fredy LD, Zotos EE. On the equilibria of the restricted three-body problem with a triaxial rigid body II: Prolate primary. Results in Physics. 2022;38:105623.
8. Bekov AA. Libration points of the restricted problem of three bodies with variable Mass. Soviet Astronomy Journal. 1988;33:92−95
9. Luk’yanov LG. Particular solutions in the restricted problem of three bodies with variable masses. Astronomical Journal of Academy of Sciences of USSR. 1989;66:180−187.
10. Singh J, Leke O. Stability of the photogravitational restricted three-body problem with variable masses. Astrophysics and Space Science. 2010;326:305−314.
11. Singh J, Leke O. Out-of-plane equilibrium points of extra-solar planets in the central binaries PSR B1620-26 and Kepler-16 with cluster of material points and variable masses. New Astronomy. 2023;99:101958.
12. Radzievskii VV. Astron.Zh (USSR). 1950;27:250.
13. Singh J, Leke O, Umar A. Analysis on Stability of triangular points in the perturbed photogravitational restricted three-body problem with variable masses. Astrophysics and Space Science. 2010;327:299−308.
14. Singh J, Leke O. Robe’s restricted three-body problem with variable masses and perturbing forces. ISRN Astronomy and Astrophysics; 2013.
15. Luk’yanov LG. Zero velocity surfaces in the restricted three-body   problem with variable masses. Soviet Astronomical Journal. 1992;68:640−648.   
16. Singh J, Simon AM. Motion around the triangular equilibrium points in the circular restricted three-body problem under triaxial luminous primaries with poynting-robertson drag. International Frontier Science Letters. 2017;12:1−21.
17. Wolfram S. The Mathematica Book, 10th Ed. Wolfram Campaigns; 2015.
18. Mestschersky IV. Works on the mechanics of bodies of variable mass (In Russia), Gosh. Izd. Tekh-Tev, Lit: Moscow; 1952. 205 p.
19. Gylden H. Astron Nachr. 1884;109:1.
20. Mestschersky IV. Ueber die Integration der Bewegungs- gleichungen im  Probleme zweier Körper von ver nderli- cher Masse. Astronomische Nachrichten. 1902;159(15):229−242.