In last few years, several cosmologists have been used different equation of states (EOS) (namely, Phantom energy, generalized Chaplygin gas, Vander Walls quintessence EOS etc) to explain the present accelerated expansion of the Universe. By using the same EOS, some theoretical physicists have been trying to construct traversable wormholes. Recent studies have proposed quardratic EOS to describe homogeneous and inhomogeneous cosmological models. In this, article we explore the possibility that the wormholes be supported by quardratic EOS. We have found a series solution of Einstein equations describing wormhole for a matter source that is characterized by quardratic EOS. Gravitational Lensing Wormhole Strong field limit.

Keywords: wormholes, chaplygin gas, quardratic EOS, Kalb-Ramond spacetime

To describe the spacetime of any massive objects (i.e. whether astrophysical objects like stars, galaxies etc or hypothetical objects like black holes, wormholes etc), it requires an interpretation of the matter content of the object. As a conventional process one can use fluid (as matter source) to study cosmological as well as astrophysical phenomena. But for matter fluid further specification of an EOS is desired. Before the acceleration of the Universe was discovered, pupils usually considered linear EOS as $p=m\rho$ (with $0\le m\le 1$). But for the last few years theoretical physicists have used different EOS (particularly, Phantom energy, the generalized Chaplygin gas, Vander Walls quintessence EOS, etc) and elucidated the causes of the expansion of the Universe in an accelerated manner. Also, it has been shown that wormholes be supported by the fluid with these different equation of states.¹ The homogeneous as well as inhomogeneous cosmological models of the universe have been suitably defined recently by Ananda et al.², by a quadratic EOS. This quadratic EOS, $p=p_0+\alpha \rho +\beta {\rho }^2$, where $p_0$ , $\alpha$ and $\beta$ are parameters, represents the Taylor series expansion of the barotropic EOS, $p\left(\rho \right)$ and $\rho$ being arbitrary. It is known that the mystery behind the expansion of the universe is dark energy or unified dark matter which can be defined by a quadratic EOS as demonstrated by Anandaet al.²

Self-sustained traversable wormhole is studied as a vacuum solution of gravitational theory³, with emphasis being given on the gravitational coupling and a possible effective gravity near the Planck scale. Modelling of wormholes within the perspective of alternative gravity theory,⁴ where an extra material term in the gravitational action is considered. Further taking into account the Starobinsky $f\left(R\right)$ model, considering a static spherically symmetric geometry with matter contents as anisotropic, isotropic, and barotropic fluids,⁵ the wormhole solutions are constructed without exotic matter, in few regions of space-time. The authors thus obtain realistic and stable wormhole solutions with anisotropic matter in the modified theory of gravity. The possibility of the existence of wormhole geometries by taking a particular model of $f\left(R\mathrm{,}T\right)=R+\alpha R^2+\lambda T$,⁶ where it is shown that in the context of anisotropic fluid and gravity, wormhole models could exist without the requirements for exotic matter. Some models of static wormholes within the $f\left(R\mathrm{,}T\right)$ extended theory of gravity are constructed where the pressure components (radial and lateral) and different equations of state.⁷ Wormhole solutions in a non-minimal torsionmatter coupled gravity,⁸ where the transfer of energy and momentum occurs between matter and torsion scalar terms. Wormhole models in modified gravity have been further discussed from studies,⁹ which is consistent with stable stellar configurations, where the second-order derivative with respect to the Ricci scalar, R, remains positive and the solution satisfies the energy conditions. The M sharif et al.¹⁰ have considered chaplygin, linear and logarithmic gas models to study the exotic matter content at thin-shell and observed that the Hoffmann-Born-Infeld parameter along with the electric charge enhance the stability regions. The correction to the standard Newtons law in terms of a polarization energy density and in presence of a spherically symmetric wormhole has been examined.¹¹ Here the authors have studied the Newtonian potential in two term, where the first term is found to be independent of the wormhole metric and corresponds to the standard law while the second term is dependent it. Nonexotic matter wormhole solutions have been obtained,¹² where a gravity theory with linear and quadratic terms of the trace of the energy-momentum tensor in the gravitational action, is considered.

String theory defines gravity, as a truly higher dimensional interaction, which eventually assumes a 4D form at low enough energies. Brane-world models, inspired by string theory, pave the novel way to corrections in GR. In comparison, where the physical fields in our 4D Universe are restricted to the 3-brane, gravity can be expressed by the extra dimension. The gravity on the brane world scenario is best represented by the modified 4-dimensional Einstein’s equations which contain (i) $S_{\mu }^{\nu }$ and (ii) $E_{\mu }^{\nu }$, representing a quadratic in terms of the stress energy tensor of matter restricted on the brane, and the trace less tensor of the 5D Weyl tensor, respectively. It is reasonable to neglect the contributions of 5D Weyl tensor in these equations. Even then the quadratic term of energy density appears in the 4-dimensional effective energy momentum tensor and plays a major role in defining the different characteristics of the models. Here lies the significance of choosing the quadratic form of the EOS. As defined earlier, this quadratic form of the EOS is rather the specific form of barotropic EOS, $p\left(\rho \right)$ where $\rho$ is arbitrary. There has been a hectic search by theoretical physicists for the matter source that is an intrinsic characteristic of the wormhole. Matter source plays a vital role for constructing wormholes, which is revealed in literature in the form of several manifesto by various authors.¹³⁻²² Authors have nicely interpreted phantom energy to describe wormhole solutions.¹³⁻²² Lobo¹⁶ has shown that Generalized Chaplygin gas may well support wormholes. Wormhole with Tachyonic field has been further studied by Das et al.²³ Casimir field can be considered as an alternative for exotic matter source, as assumed by Mansouryar²⁴ and Khabibullin A et al.²⁵ Study of wormhole in presence of C-field has been extended by F Rahaman et al. that wormhole may exist in Kalb-Ramond spacetime is also an interesting study by F Rahaman et al.²⁸ Hence we are motivated by the findings in the brane world models and try to explore the possibility that the quadratic EOS can really represent a wormhole. As a fruitful research, we find a series solution of Einstein field equations. This solution defines matter source represented by quadratic EOS and truly defines a wormhole. Hence we assume the following quadratic form of EOS₂ in terms of the energy density as,

$p=\alpha \rho +\beta {\rho }^2$ (1)

where, $\alpha \mathrm{,}\beta$ are parameters. At first we take these parameters as arbitrary, but restrictions on these parameters may be specified later.

We consider a static spherically symmetric metric in Schwarzschild co-ordinates $\left(t\mathrm{,}r\mathrm{,}\theta \mathrm{,}\varphi \right)$ as

$d{s}^2\mathrm{<mo>=</mo>}-e^{2f\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo>}}d{t}^2+\frac{1}{[1-\frac{b(r)}{r}]}d{r}^2+r^{2}d{\Omega }_2^2\mathrm{,}$  (2)

where f(r) and b(r) are known as redshift function and shape function respectively. The above metric in fact represents a Lorentzian wormhole which is defined by a manifold $R^{2}X{S}^2$ . The range of the radial coordinate is considered from $r_0$  to infinity, where $r\mathrm{<mo>=</mo>}{r}_0$  is the wormhole throat. Also the convenient ‘cutoff’ of the stress energy tensor is assumed at the junction radius ’a’.

Using the Einstein field equations $G_{\mu \nu }=8\pi T_{\mu \nu }$ , in orthonormal reference frame ( with $c=G=1$  ) , we obtain the following stress energy scenario,

$\rho \mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{b^{\text{'}}}{8\pi r^2}\mathrm{,}$       (3)

$p\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{1}{8\pi }\mathrm{<mo\; stretchy="false">[</mo>}-\frac{b}{r^3}+2\frac{f^{\text{'}}}{r}(1-\frac{b}{r})],$  (4)

$p_t\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{1}{8\pi }(1-\frac{b}{r}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">[</mo>}{f}^{\text{'}\text{'}}-\frac{\mathrm{<mo\; stretchy="false">(</mo>}{b}^{\text{'}}r-b\mathrm{<mo\; stretchy="false">)</mo>}}{2r\mathrm{<mo\; stretchy="false">(</mo>}r-b\mathrm{<mo\; stretchy="false">)</mo>}}{f}^{\text{'}}+f^{\text{'}}{}^2+\frac{f^{\text{'}}}{r}-\frac{\mathrm{<mo\; stretchy="false">(</mo>}{b}^{\text{'}}r-b\mathrm{<mo\; stretchy="false">)</mo>}}{2r^2\mathrm{<mo\; stretchy="false">(</mo>}r-b\mathrm{<mo\; stretchy="false">)</mo>}}],$  (5)

where $p\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo>}$  is the energy density, $p\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo>}$  is the radial pressure and $p_t\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo>}$  is the transverse pressure.

Using the conservation of stress energy tensor $T_{\mathrm{<mo>;</mo>}\nu }^{\mu \nu }=0$ , one can obtain the following equation

$p^{\text{'}}+f^{\text{'}}\rho +\mathrm{<mo\; stretchy="false">(</mo>}{f}^{\text{'}}+\frac{2}{r}\mathrm{<mo\; stretchy="false">)</mo>}p-\frac{2}{r}{p}_t=0.$  (6)

We take the quadratic EOS in the form

$p\mathrm{<mo>=</mo>}{p}_t\mathrm{<mo>=</mo>}\alpha \rho +\frac{\epsilon {\rho }^2}{{\rho }_c}$        (7)

The characteristic energy scale ${\rho }_c$  of the quadratic term as well as $\epsilon$  are determined by the parameter $\beta$ .

The usual perfect fluid follows a linear EOS $(\beta =0)$  with $\alpha \mathrm{<mo>=</mo>}\frac{dp}{d\rho }{|}_{\rho =0}$ . Hence $\alpha$  represents the speed of sound of the fluid and as $\rho \to 0$ , $\alpha \mathrm{<mo>=</mo>}{c}_s$ . The ${\rho }^2$  term, i.e square of the energy density in the quadratic eqn.(7) is important and one may call the high energy regime (Figure 1).

Figure 1 The variation of redshift function with respect to $\rho$ (B) The shape function of the wormhole ( retaining a few terms )for $\alpha =-\mathrm{0.1,}{b}_0=\mathrm{6.5,}{b}_1=-0.6$ (C) Energy density with respect to radial coordinate ’r’ ( retaining a few terms) for $\alpha =-\mathrm{0.1,}{b}_0=\mathrm{6.5,}{b}_1=-0.6$ .

From (6) by using (7), one can obtain

$e^{2f}\mathrm{<mo>=</mo>}{e}^{2{\rho }_0}{\mathrm{<mo\; stretchy="false">(</mo>}\frac{\rho }{{\rho }_c}\mathrm{<mo\; stretchy="false">)</mo>}}^{-\mathrm{<mo\; stretchy="false">(</mo>}\frac{2\alpha }{1+\alpha }\mathrm{<mo\; stretchy="false">)</mo>}}{\left[\frac{\epsilon \rho }{{\rho }_c}+1+\alpha \right]}^{\frac{-2(2+\alpha )}{1+\alpha }},$  (8)

where ${\rho }_0$  is an integration constant.

Taking into account equations (3)-(8), we have the following equation containing ’b’ as

$\frac{\alpha (1+\alpha ){b^{\text{'}}}^2}{8\pi r^4}+\frac{\epsilon (1+2\alpha ){b^{\text{'}}}^3}{64{\rho }_c{\pi }^2{r}^6}+\frac{{\epsilon }^2{b^{\text{'}}}^4}{512{\rho }_c^2{\pi }^3{r}^8}=\frac{\alpha b{b}^{\text{'}\text{'}}}{4\pi r^4}-\frac{\alpha b^{\text{'}\text{'}}}{4\pi r^3}+\frac{\alpha b^{\text{'}}}{2\pi r^4}$

$-[\frac{\alpha }{2\pi }+\frac{(1+\alpha )}{8\pi }]\frac{b{b}^{\text{'}}}{r^5}-\frac{\epsilon b^{\text{'}}{b}^{\text{'}\text{'}}}{16{\rho }_c{\pi }^2{r}^5}+\frac{\epsilon b{b}^{\text{'}}{b}^{\text{'}\text{'}}}{16{\rho }_c{\pi }^2{r}^6}+\frac{\epsilon {b^{\text{'}}}^2}{8{\rho }_c{\pi }^2{r}^6}$

$-\frac{\epsilon b{b^{\text{'}}}^2}{r^7}(\frac{1}{64{\pi }^2{\rho }_c}+\frac{1}{8{\pi }^2{\rho }_c})\mathrm{.}$

Now to investigate whether there exists physically meaningful solutions consistent with the boundary requirements , we take a general functional form of $b\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo>}$ . We can generally express it in the form

$b\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\Sigma }_{n\mathrm{<mo>=</mo>1}}^{\infty }{a}_n{r}^n+{\Sigma }_{m\mathrm{<mo>=</mo>0}}^{\infty }{b}_m{r}^{-m}$       (9)

since $\frac{b\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo>}}{r}\to 0$  as $r\to \infty$ , equation (10) is consistent only when all the $a_n$ ’s in $b\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo>}$  vanish i.e.

$b\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\Sigma }_{m\mathrm{<mo>=</mo>0}}^{\infty }\frac{b_m}{r^m}$     (10)

Plugging this in equation (9) and matching the coefficients of equal powers of $r$  from both sides, we get ,

$br{b}_0+\frac{b_1}{r}+\frac{1}{r^2}\left[\frac{(1+9\alpha )b_0{b}_1}{20\alpha }\right]$

$+\frac{1}{r^3}\left[\frac{(1+9\alpha )(1+11\alpha )b_0^2{b}_1}{360{\alpha }^2}\right]+\mathrm{......,}$ (11)

with $b_0$  and $b_1$  is arbitrary constant.

Now expression for $\rho$ can be obtained from (3) as

$\rho \frac{1}{8\pi }\left[\frac{-b_1}{r^4}-\frac{(1+9\alpha )b_0{b}_1}{10\alpha r^5}\right]$

$-\frac{1}{8\pi r^6}\left(\frac{(1+9\alpha )(1+11\alpha )b_0^2{b}_1}{120{\alpha }^2}-\frac{({\alpha }^2-8\alpha -1)b_1^2}{12\alpha }\right)-\mathrm{......,}$

Here $\rho >0$  implies $b_1$  should be negative.

The throat of the wormhole occurs at $r\mathrm{<mo>=</mo>}{r}_0$  where $r_0$  is the solution of the equation $b\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}r$ . Suppose $\frac{1}{r}\mathrm{<mo>=</mo>}y$ , then $b\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}r$  implies

$g\mathbf{\left(}y\right)=b_{0}y+b_1{y}^2+b_2{y}^3+\mathrm{............}-1=0.$ (12)

This is an algebraic equation with negative last term. Then this equation must have at least one positive root, say, $y\mathrm{<mo>=</mo>}\frac{1}{r_0}$ . Since $\frac{1}{r_0}$  is a root of equation (14), then by standard theorem of algebra, either $g\left(y\right)>0$  for $y\mathrm{<mo>></mo>}\frac{1}{r_0}$  and $g(y)<0$  for $y\mathrm{<mo><</mo>}\frac{1}{r_0}$  or $g\left(y\right)<0$ for $y\mathrm{<mo>></mo>}\frac{1}{r_0}$ and $g\left(y\right)>0$  for $y\mathrm{<mo><</mo>}\frac{1}{r_0}$ . Let us take the first possibility and one can note that for $y\mathrm{<mo>=</mo>}\frac{1}{r}\mathrm{<mo><</mo>}\frac{1}{r_0}$  i.e. $r\mathrm{<mo>></mo>}{r}_0$ , $g\left(y\right)<0$ , in other words, $b\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo><mo><</mo>}r$ . But when $y\mathrm{<mo>=</mo>}\frac{1}{r}\mathrm{<mo>></mo>}\frac{1}{r_0}$  i.e. $r\mathrm{<mo><</mo>}{r}_0$ , $b\left(r\right)>r$ , this means, $b\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo><mo>></mo>}r$ , which violates the wormhole structure given in equation(2).

According to Morris et al.²⁹ the ’r’ co-ordinate is ill-behaved near the throat, but proper radial distance

$l\left(r\right)=\pm {\int }_{r_0^{+}}^r\frac{dr}{\sqrt{1-\frac{b\left(r\right)}{r}}}$     (13)

must be well behaved everywhere i.e. we must require that $l\left(r\right)$ is finite throughout the space-time.

For our Model,

$l\left(r\right)=\pm {\int }_{r_0^{+}}^r\frac{dr}{\sqrt{1-\frac{1}{r}{b}_0+\frac{b_1}{r}+\frac{b_2}{r^2}+}}\mathrm{.}$     (14)

Though we cannot find the explicit form of the integral but one can see that the above integral is a convergent integral i.e. proper length should be finite.

The axially symmetric embedded surface $z=z\left(r\right)$ shaping the Wormhole’s spatial geometry is a solution of

$\frac{dz}{dr}=\pm \frac{1}{\sqrt{\frac{r}{br}-1}}$      (15)

One can note from the definition of Wormhole that at $r=r_0$ (the wormhole throat) Eq.(14) is divergent i.e. embedded surface is vertical there.

The embedded surface (solution of eq.(14) ) in this case

$z=\pm \sqrt{b_0}\sqrt{r}-b_0^2+b_1{r}^{-\frac{1}{2}}-\left(\frac{7b_0^2+2b_0{b}_1+3b_1^2+4b_2}{12}\right)r^{-\frac{3}{2}}$

$-\left(\frac{12b_0{b}_2+7b_0{b}_1+3b_1^2+8b_3}{40}\right)r^{-\frac{5}{2}}\mathrm{.....}]$

One can see that embedding diagram of this wormhole (retaining a few terms) in Figure 2. The surface of revolution of the curve about the vertical z axis makes the diagram complete (Figure 2).

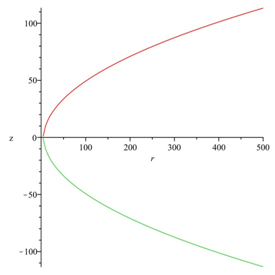
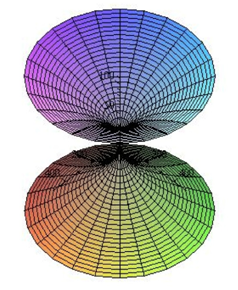
Figure 2 (A) The embedding diagram of the wormhole for $\alpha =-\mathrm{0.1,}{b}_0=\mathrm{6.5,}{b}_1=-0.6$ (B) The full visualization of the surface generated by the rotation of the embedded curve (retaining a few terms) about the vertical z axis.

The major thrust in this article is to explore the matter ingredients characterized by quadratic EOS that produces wormhole akin spacetime. We are indeed triumphant in our work to exhibit that wormhole can be supported by quadratic EOS. It is easy to verify that the shape function of the wormhole satisfies all the desired conditions to represent a wormhole. The resulting line element represents an one parameter ($b_1$) family of geometries which contains wormholes. If $b_1=0$, then $\rho =p=0$. And one obtains the standard Schwarzschild solution, viz., $e^{2f\left(r\right)}=[1-\frac{b\left(r\right)}{r}]=1-\frac{r_s}{r}$, provided $b_0=r_s=2M$ ( the Schwarzschild radius). The asymptotical wormhole mass reads $M={\lim }_{r\to \infty }\frac{1}{2}b\left(r\right)=\frac{b_0}{2}$. Also as the parameter $b_0>0$, the asymptotic mass ‘M’ of the wormhole is positive, hence a distant observer could not distinguish between the gravitational nature of the wormhole and a compact mass ‘M’.

FR is thankful to DST-SERB, Government of India for providing research support.

1. F Lobo. Traversable wormholes supported by cosmic accelerated expanding equations of state. 2006.
2. K Ananda, M Bruni. Cosmological dynamics and dark energy with a quadratic equation of state: Anisotropic models, large-scale perturbations, and cosmological singularities. Phys Rev D. 2006;74:023524.
3. E Contreras, Pedro Bargueo. A self-sustained traversable scale-dependent wormhole. Int J Mod Phys D. 2018;27(9):1850101.
4. PK Sahoo, PHRS Moraes, P Sahoo et al. Phantom fluid supporting traversable wormholes in alternative gravity with extra material terms. Int J Mod Phys D. 2018;28:1950004.
5. M Zubair, S Waheed, Y Ahmad. Static spherically symmetric wormholes in f(R, T) gravity. Eur Phys J C. 2016;76:444.
6. Z Yousaf, M Ilyas, M Zaeem-ul-Haq Bhatti. Static spherical wormhole models in f(R,T) gravity. Eur Phys J Plus. 2017;132: 268.
7. PHRS. Moraes, PK. SahooModeling wormholes in f(R,T) gravity. Phy Rev D. 2017;96:044038.
8. A Jawad, S Rani. Non-minimal coupling of torsion–matter satisfying null energy condition for wormhole solutions. Eur Phys J C. 2016;76:704.
9. PK Sahoo, PHRS Moraes, Parbati Sahoo. Wormholes inR2 -gravity within the f(R,T) formalism. Eur Phys J C. 2018;78:46.
10. M Sharif, S Mumtaz. Dynamics of thin-shell wormholes with different cosmological models. Int J Mod Phys D. 2017;26(5):1741007.
11. AA Kirillov, EP Savelova. Modification of gravity by a spherically symmetric wormhole. Int J Mod Phys D. 2017;26:1750145.
12. PHRS Moraes, PK Sahoo. Nonexotic matter wormholes in a trace of the energy-momentum tensor squared gravity. Phys Rev D. 2018;97:024007.
13. S Sushkov. Wormholes supported by a phantom energy. Phys Rev D. 2005;71:043520.
14. Francisco SN Lobo. Phantom energy traversable wormholes. Phys Rev D. 2005;71:084011.
15. Francisco SN Lobo. Stability of phantom wormholes. Phys Rev D. 2005;71:124022.
16. Francisco SN Lobo. Chaplygin traversable wormholes. Phys Rev D. 2005;73:064028.
17. P Kuhfittig. A wormhole with a special shape function. Am J Phys. 1999;67:125.
18. O Zaslavskii.Exactly solvable model of wormhole supported by phantom energy. Phys Rev D. 2005;72:061303.
19. F Rahaman, M Kalam, M Sarker, et al. A theoretical construction of wormhole supported by Phantom Energy. Physics Letters B. 2006;633(2-3):161−163.
20. F Rahaman, M Kalam, S Chakraborty. Wormholes with varying equation of state parameter. arXiv:gr-qc/0701032.
21. F Rahaman, M Kalam, M Sarker, et al. Wormhole with varying cosmological constant. Gen Rel Grav. 2007;39:145−151.
22. F Rahaman, M Kalam, BC Bhui, et al. Construction of a 3D wormhole supported by phantom energy. Phys Scr. 2007;76(1):56.
23. A Das, S Ka. The Ellis wormhole with `tachyon matter'. Class Quant Grav. 2005;22(14):3045.
24. M Mansouryar. On a macroscopic traversable spacewarp in practice. arXiv:gr-qc/0511086.
25. Artem R Khabibullin, Nail R Khusnutdinov, Sergey V Sushkov. Casimir effect in a wormhole spacetime. Class Quant Grav. 2006;23(3):627−634.
26. F Rahaman, BC Bhui, P Ghosh. Wormhole and C-field. Nuovo Cim B. 2004;119:1115−1119.
27. F Rahaman, M Kalam, S Chakraborty. Gravitational lensing by stable C-field wormhole. arXiv:0705.0740 [gr-qc].
28. F Rahaman, M Kalam, A Ghosh. Existence of Wormholes in Einstein-Kalb-Ramond space time. Nuovo Cim B. 2006;121:303−307.
29. M Morris, K Thorne, Kip S Thorne. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. American J Phys. 1988;56:39.