An analysis of the complete solutions of the linearized system of fundamental equations for weakly dissipating media was performed by methods of singular perturbations. Regular functions of complete solutions describe waves of different types. Singularly perturbed solutions describe a wide class of ligaments–previously unknown high gradient components of flows supplementing well investigated propagating waves. All flow components that are internal waves, vortices and ligaments were observed in a stratified wake past a vertical plate. Ligaments are classified as linear precursors of shock waves.

As the system of fundamental equations is invariant with respect temporal and spatial scales the basic flows components that are waves, vortices and ligaments are universal and exist in the whole range of the fluid flows from microscopic to macroscopic length scales.

Keywords: set of fundamental equation, complete solutions, internal waves, vortices, ligaments, experiment

Descartes¹ in his remarkable treatise “Principia philosophiae" presented definition of the vortex as a flow in which a body rotating around the axis of the current is spinning simultaneously relative to its own axis, and added schematic drawing of space, containing bounded vortex cells with a pronounced internal linear structure.¹ Subsequent careful astronomical observations of a "light echo" produced by exploding stars really confirmed the existence of a pronounced line structure in a pattern of matter in interstellar space and the remnants of blowing stars.² Systematic observations have shown existence of a fine structure in fields of physical quantities in the ocean³ and in the atmosphere, where thin strip like elements bounded by a high gradient interfaces were recognized. They were continuously traced during long time, which was significantly larger than the characteristic dissipative and diffusion time scales.

Laboratory studies of stratified flows have shown that regular images of thick layers with internal filaments ("salt fingers") separated by high gradient interfaces are observed in patterns of smaller scales flows in particular in compact vortices, convective cells of double diffusive or multi‒component convection, in drying droplets of micro and nanoparticles suspensions.⁴ Regular lined structures were observed in fast small scale phenomena developing when a freely falling drop impacts on targeting fluid.⁵ That is, the structuring in spatial patterns in fields of matter is observed throughout the complete range of spatial scales accessible to experimental study. The length scales of structures are extending from astronomical units to micrometers, and time scales from millions of years to microseconds.

However, the universal mathematical model of such a universal and steadily observable property of natural flows has not been completed up to date. In this paper, the mathematical classification of the structural components of periodic flows, based on an analysis of the solutions of the fundamental system of equations with taking into account the compatibility condition is presented. Special attention is paid to the analysis of the approximation of a homogeneous fluid, which is traditionally used in describing fluid flows in natural and technical conditions. It should be noted that the class of periodical flows directly include the problems of a transient flow where the role of the period is given to time of fast flow evolution.

In the fluid mechanics, the main fluid parameters that are a density$\rho \left(x,t\right)$ , characterizing its inertial and gravitational properties, other thermodynamic parameters–pressure$P\left(x,t\right)$ ,temperature$T\left(x,t\right)$ , concentration of dissolved impurities or suspended particles $S_i\left(x,t\right)$ , momentum$p$ or velocity$v$ , related by the relationship $p=\rho v$ , and the energy, including mechanical and internal components, are functions of coordinates$x$ and time $t$ . To simplify description of incompressible media the set of linearized fundamental governing equations is selected in the conventional form with temperature instead of energy⁶

$\frac{\partial \rho }{\partial t}+div\rho v=0$     (1)

$\frac{\partial \rho v}{\partial t}=-\nabla P+\rho \nu \Delta v+\left(\zeta +\frac{1}{3}\rho \nu \right)\nabla \mathrm{div}v+\rho g$     (2)

$\frac{\partial \rho T}{\partial t}={\kappa }_T\Delta \rho T$      (3)

$\frac{\partial \rho S_i}{\partial t}={\kappa }_{S_i}\Delta \rho S_i$   (4)

Where$\nu ,\zeta ,{\kappa }_T,{\kappa }_{S_i}$ are coefficients of first and second kinematic viscosities, temperature and salinity diffusivity.
The system (1–4) is analyzed taking into account the condition of compatibility, which defines its rank. The rank of the set (1–4) is tenth and complete solution contains ten independent functions.

Three dimensional periodic flows with a constant positive frequency$\omega$ and a complex wave number$k=\left(k_x,k_y,k_z\right)$ , $k=k_1+i{k}_2$  are considered, the imaginary part of which, characterizing the spatial attenuation of the wave fields coefficients, is supposed to be small.

The equations of system (1–4), in which the small coefficients stand for terms with the highest derivatives with respect to spatial variables, belong to the class of singularly perturbed equations. To obtain complete solutions of such equations, it is necessary to use both converse and reverse expansions in the small parameter of the form

$k=k_0+\epsilon k_1+{\epsilon }^2{k}_2+\mathrm{...}$         (5)

$k_z={\epsilon }^{-\gamma }\left(k_0+\epsilon k_1+{\epsilon }^2{k}_2+\mathrm{...}\right),\gamma >0$                (6)

The value of the coefficient$\gamma$ is determined by substituting (5),(6) into the system of equations under consideration from the precedence condition of the resulting principal term of the expansion. When studying small periodic motions with a real frequency$\omega$ and a complex wave vector$k$ , all the variables are chosen in the form

$v=v_0\tau (r,t)$ ,$\overline{p}=p_0\tau (r,t)$ ,$\overline{\rho }={\rho }_0\tau (r,t)$ , $\tau (r,t)=\exp \left(i(kr-\omega t)\right)$             (7)

The solution of the system (1–4) for waves propagating in an unbounded medium is searched in the form of expansions in plane waves

$A={\displaystyle \sum _j{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{a}_j\left(k_x,k_y\right)\exp \left(i\left(k_{zj}\left(k_x,k_y\right)z+k_{x}x+k_{y}y-\omega t\right)\right)}d{k}_{x}d{k}_y}}$           (8)

Where$A$  are components of velocity, density, pressure, salinity or temperature.

The summation in the expansion (8) is carried out over all the roots of the dispersion equation expressing the condition for the solvability of the linearized system (1–4), which satisfy the boundary conditions of the problem or the radiation condition in an infinite distance from the source (or attenuation of all perturbations at infinity).

Substituting expansions of functions for all physical variables into the system (1–4) and taking into account the compatibility condition for equations, one can find the dispersion relation, which, taking into account the action of all the dissipative factors, has the form

$D_{\nu }(k,\omega )\cdot F(k,\omega )=0$           (9)

Where
$\begin{array}{l}F(k,\omega )=-D_{\nu }(k,\omega )D_{{\kappa }_T}(k,\omega )D_{{\kappa }_S}(k,\omega )\left(k^2+i\frac{k_z({\Lambda }_T+{\Lambda }_S)}{{\Lambda }_T{\Lambda }_S}\right)+\\ +D_{{\kappa }_T}(k,\omega )\left(\frac{\omega k_z}{{\Lambda }_S}{D}_{\nu }(k,\omega )-N_S^2{k}_{\perp }^2\right)+D_{{\kappa }_S}(k,\omega )\left(\frac{\omega k_z}{{\Lambda }_T}{D}_{\nu }(k,\omega )-N_T^2{k}_{\perp }^2\right)\end{array}$   (10)

$D_{\nu }(k,\omega )=-i\omega +\nu k^2$ , $D_{{\kappa }_T}(k,\omega )=-i\omega +{\kappa }_T{k}^2$ , $D_{{\kappa }_S}(k,\omega )=-i\omega +{\kappa }_S{k}^2$ , $k^2=k_x^2+k_y^2+k_z^2$ ,$k_{{}^{\perp }}^2=k_x^2+k_y^2$ .

Disregarding all the dissipative effects, the dispersion equation of the tenth degree (9) goes into a quadratic equation describing the internal waves in an ideal fluid (and all other types of waves are inertial, surface gravitational, acoustic and hybrid in general case taking into account rotation and compressibility effects). The spectral components, in which $\left|k_1\right|>>\left|k_2\right|$ (7), the damping factor is proportional to the kinetic coefficients (here$\gamma =i\left(\nu +{\kappa }_T+{\kappa }_S\right)k^2$ ), are regular perturbed components of flow and describe the large scale wave components of periodic flows. Regularly perturbed solutions of the algebraic equation (9) and the system of differential equations (1–4) correspond to it, satisfying to the boundary conditions, respectively, determine the conical beams of periodic internal waves.⁷

The remaining eight roots of equation (9), the imaginary part of which is not small ($\left|k_1\right|~\left|k_2\right|$ ) and inversely proportional to the kinetic coefficients, define ligament–singular perturbed solutions, characterizing the fine structure of flows. In the case of an infinite medium, four of them, which do not satisfy the damping boundary condition at infinity, were discarded. The remaining solutions for ligaments form two distinct groups. From the form of equation (9), in which the multiplier $D_{\nu }(k,\omega )=0$  is present, it follows that all fluid flows are structured and the waves always coexist with fine singularly perturbed solutions (such as the periodic Stokes boundary layer on an oscillating surface in a viscous liquid). However, these fine flow components are located not only at the boundaries, but also inside the fluid volume involved in the studied motion where they form family of ligaments. The transverse length scale (thickness) of ligaments are determined by the kinematic viscosity and frequency of the wave ${\delta }_{\omega }^{\nu }=\sqrt{\nu /\omega }$  (or buoyancy frequency${\delta }_N^{\nu }=\sqrt{\nu /N}$ ).

Simultaneously, the dissipative effects determine the existence of other flow components whose properties are described by the second and third terms in (10). Their transverse sizes depend on the frequencies or and the values of all the kinetic coefficients (kinematic viscosity, thermal and components diffusivities), as well as on the direction of wave propagation (in case of internal waves by the slope of the group velocity vector to the horizon or to the radiating surface (here by the ratio$k_z/k$ ). Ligaments that are singularly perturbed components of complete solutions are linear precursors of vortices, vortex systems and shock waves in fluid flows.

All solutions of the set (1–4), which are regularly and singularly perturbed, form a common family described by functions of one form (4.8), which differ in the magnitude of the ratios of the real and imaginary parts. All of them are formed, transferred and disappear simultaneously, despite the differences in characteristic length scales. Each of components of the flows causes the transport of energy, matter and vorticity.

The dispersion relation that fixes an experimentally verifiable functional relationship between the parameters of the instantaneous spatial structure of the medium (length scale or wave numbers) and a local time characteristic (the period of variations) determines the concepts of definition for both waves and ligaments structurally large and fine components of flows. Properties of waves are characterized by regular solutions of the fundamental set. Ligaments are singular solutions describing elongated and thin 2D (surface) and 1D (linear) flow components. In linear models, ligaments and waves are described by independent functions. In weakly nonlinear all of them interact with each other⁸ and produce nonlinear waves and shock waves. Really observed surface and line fine flow components are product of non‒linear interactions of all ligaments described by the family of singular perturbed solutions. In this sense, the ligaments can be treated as linear precursors of shock waves.

To reduced system of equations for periodic motions (1–4) of an incompressible homogeneous fluid in the phase space $\left(\omega ,k\right)$

$\left(\omega +i\nu \right)v_{i0}+k_i{P}_0=0,k_x{v}_x{}_0+k_y{v}_y{}_0+k_z{v}_z{}_0=0$           (11)

Corresponds the dispersion equation

$k^2{\left(\omega +i\nu k^2\right)}^2=0$               (12)

The first multiplier$k^2=0$ in equation (12) with the solution in the form$k_z=\pm i\sqrt{k_x^2+k_y^2}$ represents in a collapsed form all kinds of wave processes caused by the effect of compressibility, stratification, rotation, and other physical factors in inhomogeneous liquids in external force fields.

The second multiplier in the dispersion equation (12) defines a pair of identically singular perturbed solutions for identical ligaments

${\left(\omega +i\nu k^2\right)}^2=0$    (13)

Since$k\ne 0$ , then from (12) and (13) it follows that$P=0$ . The solution has the character of a degenerate internal periodic boundary layer, in the plane of whose centers$v_z=0$ , and the values of the velocity components$v_x$ , $v_y$  depend on the local normal coordinate$z$ .

In a compressible medium, the dispersion equation corresponding to the reduced part of the complete system, which includes only equations (1, 2), has the form

$\left(k^2\left(1-\frac{i\omega \tilde{\nu }}{c_s^2}\right)-\frac{{\omega }^2}{c_s^2}\right){\left(\omega +i\nu k^2\right)}^2=0$               (14)

Where$\tilde{\nu }=\zeta +4\nu /3$ ;$\nu$ ,$\zeta$ are shear (first) and convergence (second) kinematic viscosity,$c_s$ is the sound velocity. The first multiplier in (14) is the classical dispersion relation for a sound wave in a dissipative medium, which describes waves with a frequency$\omega$ and wave vector$k$ propagating with a velocity${с}_s$ . The second multiplier is a doubly degenerate singularly perturbed solution of Stokes type, describing two merged identical ligaments. Consequently, therefore, the account of compressibility does not remove the degeneracy of the equations set for a homogeneous fluid.

The system of governing equations for a viscous inhomogeneous incompressible exponentially stratified fluid which is characterized by the buoyancy scale${\Lambda }_{\rho }={\left|d\ln \rho /dz\right|}^{-1}$ , frequency $N=\sqrt{g/\Lambda }$  and period $T_b=2\pi /N$  is usually written in the form

$\begin{array}{l}\frac{\partial \tilde{\rho }}{\partial t}-\frac{v_z}{\Lambda }=0,divv=0\\ {\rho }_0(z)\frac{\partial v_i}{\partial t}=-\frac{\partial \tilde{p}}{\partial x_i}+\nu {\rho }_0(z)\Delta v_i-{\delta }_{i3}\tilde{\rho }g\end{array}$              (15)

Where$\rho ={\rho }_0(z)+\tilde{\rho }\left(x,t\right)$ , $P=P_0(z)+\tilde{P}\left(x,t\right)$ .

The dispersion equation of system (15) has the form

$\left({\omega }^2{k}^2-N^2{k}_{\perp }^2+i\omega \nu k^4\right)\left(\omega +i\nu k^2\right)=0$           (16)

Solutions (16) are either internal waves whose oscillations occur in the direction of the wave propagation (the group velocity), which are accompanied by two kinds of different ligaments describing the fine structure components of the flows in the volume and on the boundary of the medium. It should also be noted, that from the no slip boundary condition on the fixed reflecting wave plane it follows that the oscillations in the internal waves (incident and reflected) and in formed the boundary layer are in antiphase.

In one dimensional and two dimensional formulations, all the considered types of model equations are solvable. In the three dimensional case in a homogeneous compressible and incompressible fluid, the complete solution of the linear system is degenerate with respect to the singular components.

Stratification ensures the existence of two different types of singularly perturbed solutions, which removes second order degeneracy in problems of radiation, propagation or reflection of internal waves from an inclined surface. Complete classification of periodic motions in viscous stratified and rotating medium is given in.9 With increasing of the flow velocity fine ligaments interact between themselves and form pronounced fine components including tangential discontinuities and shock waves.

All images of flow patterns can be registered by sensitive optic instrument with a high spatial resolution, for example in observation of stratified flows. The typical schlieren side view image of flow produced by the uniformly towing vertical plate is given in Figure 1. In the experiments the plate with height$h=2.5\text{cm}$ was uniformly towed with velocity$U=0.87\text{cm/s}$ in the rectangular tank filled with continuously stratified common salt solution with buoyancy period $T_b=12.7\text{s}$ (coefficient of kinematic viscosity is$\nu =0.01{\text{cm}}^{\text{2}}\text{/s}$ and salinity diffusivity is ${\kappa }_S=1.43{\text{cm}}^{\text{2}}\text{/s}$ ). Schlieren instrument IAB‒458 with aperture 23 cm with vertical illuminating slit and vertical Foucault knife was used for flow visualization. In this instrumental configuration, the variations of the horizontal components of the index of refraction gradient (or the fluid density gradient) define the brightness of the schlieren image of the flow pattern.

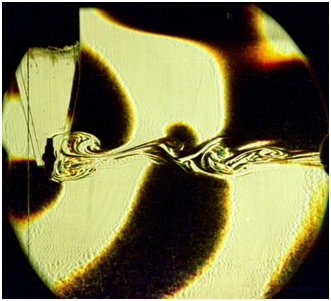
Figure 1Classical schlieren image of the flow pattern including upstream disturbances, attached internal waves and vortices and ligaments in the downstream wake past uniformly moving vertical plate ($T_b=12.7\text{s}$ , $h=2.5\text{cm}$ , $U=0.87\text{cm/s}$ ).

The main part of the flow pattern is covered by semi‒circular light and dark strips visualizing attached internal waves. Sharp boundaries between strips are crests and troughs of the waves. In the wake past the strip, the rear vortex and the “vortex bubble” are distinguished. Ahead of the strip, black and light bands denote upstream disturbances. Past the body, a wake with rich layered fine structure is visualized.

Vortices inside the wake are bounded by a high gradient envelope (the boundary ligament) separating domains with vortex and waves flow structures. Rear and bubble vortices are connected by the family of linear and loops ligaments forming by the set of sharp fine interfaces. Separate ligaments are described by singular perturbed solutions of the general set (1–4).

Analysis of the fundamental equations system complete solutions has shown existence of two types solutions: regularly and singularly perturbed. Regular solutions describe waves of different types (inertial, internal and surface gravity, acoustical). Singularly perturbed solutions describe ligaments that are extended fine surfaces and filaments with a high gradient of physical quantities.

Equations of 3D flows of homogeneous compressible and incompressible media are classified as degenerated as at least two singularly perturbed solutions become identical. The equation set of 6^th rank for 4 physical variables (pressure and three component of the velocity) is over determined and ill posed.

The equations set become well‒posed when variations of density are taken into account and all flow components that are waves, vortices and ligaments, are investigated. In schlieren images of stratified flows the internal waves form specialized regular pattern, vortices are bounded by a high gradient envelope and ligaments manifest themselves as family of high gradient filaments and surfaces inside the fluid bulk and on boundaries of regions of intensive fluid motions.

The system of the fundamental equations is universal and describes flows in all temporal and spatial scales and the basic flows components that are waves, vortices and ligaments exist in the whole range of the fluid flows from microscopic to macroscopic length scales.

The work was carried out with the partial financial support of the IPMekh RAS (project AAAA‒A17‒117021310378‒8 – Development of coordinated analytical numerical methods for calculating the dynamics and structure of fluid flows and comparison techniques with the data of high‒resolution experiments at the USU "GFK IPMekh RAS" stands) and RFBR (grant 18 ‒05‒00870.)

Author declares there is no conflict of inertest.

1. Descartes R. Principles of Philosophy. Amstelodami:Apud Ludovicum Elzevirium Publication; 1644. 620 p.
2. https://www.nasa.gov/multimedia/imagegallery/image_feature_2472.html
3. Fedorov KN. The thermohaline fine structure of the ocean. UK: Pergamon press; 1978. 179 p.
4. Chashechkin YD, Bardakov RN, Shabalin VV. The regular fine structure of flows in a drying drop of a suspension of quartz nanoparticles. Doklady Physics. 2011;56(1):62–64.
5. Ilynykh AY, Chashechkin YD. Hydrodynamics of a submerging drop: lined structures on the crown surface. Fluid dynamics. 2017;52(2):309–320.
6. Vallis GK. Atmospheric and oceanic fluid dynamics. UK: CUP; 2006. 745 p.
7. Bardakov RN, Vasilev AY, Chashechkin YD. Calculation and Measurement of Conical Beams of Three-Dimensional Periodic Internal Waves Excited by a Vertically Oscillating Piston. Fluid Dynamics. 2007;42(4):612–626.
8. Kistovich YV, Chashechkin YD. A new mechanism of the nonlinear generation of internal waves. Doklady Physics. 2002;47(2):163–167.
9. Chashechkin YD. Differential fluid mechanics–harmonization of analytical, numerical and laboratory models of flows. Mathematical Modeling and Optimization of Complex Structures. 2016;4:61–91.