The stability of ball lightning is analyzed. According to the electrodynamic model, the ball lightning consists of an energy core in the form of an ensemble of dynamic electric capacitors located inside a spherical shell of water. The dynamic capacitor consists of electrons and protons rotating in closed orbits. The shell tends to stretch under the force F_cf, which is_, proportional to the kinetic energy of protons E_k, and the force F_el, proportional to the square of the uncompensated electric charge of the core Q². The shell is compressed by the force F_sh proportional to its thickness a and the charge Q, as well as the atmospheric pressure force P_a. It is shown that, provided that the radius R of ball lightning can change only due to the work of internal forces, its size remains unchanged. The stability of the size of ball lightning is maintained under the balance of the rate of loss of its energy reserve E_k and the charge Q. If this balance is disturbed, an explosion of ball lightning or its collapse may occur. The relationship between the main parameters of ball lightning is considered: its energy E_k, charge Q, shell thickness a and shell radius R. The conditions for accumulation of maximum energy at a minimum shell thickness are found. The results of calculating the parameters of ball lightning with energy of 10-2300 MJ are compared with the parameters of observed high-energy ball lightning. It is shown that these data are in good agreement with each other.

Keywords: Ball lightning; Dynamic electric capacitor; Balance of forces; Stability test; Lifetime

In the previous article,¹ we discussed the structure of ball lightning with an energy core, which consists of an ensemble of “dynamic electric capacitors”. A dynamic electric capacitor is a system of electrons moving in closed orbits and with protons rotating around them. This system tends to expand, so it can only exist inside a vessel that creates pressure that restrains the expansion of the dynamic capacitors. The force that creates this pressure appears due to the polarization of the vessel material (the shell of the ball lightning) in the non-uniform electric field created by the charge of the ensemble of dynamic capacitors. Natural ball lightning can remain stable for tens of minutes. Therefore, the first problem to be discussed is how the stability of ball lightning, arranged according to the scheme of the electrodynamic model, is maintained. Ball lightning is an object interacting with the external environment. Ball lightning loses energy through radiation and constantly loses charge. Therefore, an adequate model of ball lightning should answer the question of the reasons for maintaining the stability of the size of ball lightning under the conditions of its interaction with the environment and provide an explanation for the cases of explosion or collapse of ball lightning when the conditions of this stability are violated. Ball lightning that occurs at high altitudes² is formed under conditions of a deficit of material for creating a shell (water). Therefore, it is interesting to discuss the conditions of existence of ball lightning with a minimum shell volume. In this article, we will try to find answers to these questions.

Analysis of the stability conditions of ball lightning

Let us determine the balance of forces stretching and compressing the shell of ball lightning. Let us consider a spherical shell of thickness a with an internal radius R, inside which there is one dynamic capacitor. The radius of the proton orbit in this core is R, the orbital velocity of the protons is v_p, and their total mass is M_p. For non-relativistic protons, the centrifugal force is

$F_{cf}=\frac{M_p{v}_p^2}{R}=\frac{2E_k}{R}.$            (1)

Here E_k is the kinetic energy of the protons (which we will agree to consider equal to the energy of ball lightning). In addition to the centrifugal force, the orbit of the rotating protons is additionally stretched by the force F_el, caused by the Coulomb repulsion of charges and the magnetic field created by the current of the ring. We will assume that only the uncompensated part of the total charge of the protons Q = Q_p – Q_e takes part in the creation of this force. This force is equal to:³

$F_{el}=\frac{k{Q}^2}{8\pi {\epsilon }_0{R}^2},$                       (2)

where k = (1+β²)L/π, β = v_p/c, c is the speed of light, L = ln[16R/(a_r+a_z)], a_r and a_z are the radial and axial semi-axes of the current ring cross-section. Taking v_p = 1.5·10⁸ m/s, we find 1+ β² = 1.25. If  a_r + a_z = 0.1R, then L ≈ 5, and k ≈ 2.

The force F_sh compressing a shell of thickness a due to the gradient of the electric field:

$F_{sh}=\sigma agradE·4\pi R^2= -\frac{4\sigma aQ}{{\epsilon }_0(2R+a)}.$ (3)

Here σ is the surface charge density of the dipoles on the surface, σ = 1 C/m². The second force compressing the shell is the force of atmospheric pressure p = 10⁵ Pa:

$F_a = –p·4\pi R^2.$                   (4)

The condition of the shell equilibrium is the balance of all forces acting on it:

$F=F_{cf}+F_{el}+F_{sh}+F_a=\frac{2E_k}{R}+\frac{k{Q}^2}{8\pi {\epsilon }_0{R}^2}-\frac{4\sigma aQ}{{\epsilon }_0(2R+a)}-4\pi p{R}^2=0.$                       (5)

The equilibrium of the system will be stable if the derivative dF/dR (at F = 0) is negative, that is, as the radius of the shell R increases, the force stretching it will decrease ⁴. Differentiating F with respect to R, we obtain:

$\frac{dF}{dR}=-\frac{2E_k}{R^2}+\frac{2}{R}\frac{d{E}_k}{dR}-\frac{2k{Q}^2}{8\pi {\epsilon }_0{R}^3}+\frac{8\sigma aQ}{{\epsilon }_0{(2R+a)}^2}-\frac{8\sigma RQ}{{\epsilon }_0{(2R+a)}^2}\frac{da}{dR}-8\pi pR.$            (6)

From the condition of constancy of the shell volume V_en = (4π/3)[(R+a)³– R³] = const, (dV_en/dR = 0), we find

$\frac{da}{dR}=-\frac{a(2R+a)}{{(R+a)}^2}.$ (7)

According to formula (5), under equilibrium conditions F = 0 and

$\frac{2E_k}{R^2}=\frac{4\sigma aQ}{{\epsilon }_0(2R+a)R}+4\pi pR-\frac{k{Q}^2}{8\pi {\epsilon }_0{R}^3}.$         (8)

When the internal radius of the shell R increases by dR, the kinetic energy of the ions decreases by an amount equal to the work against the forces compressing the shell:

$-d{E}_k=\left[\frac{4\sigma aQ}{{\epsilon }_0(2R+a)}+4\pi p{R}^2\right]dR.$          (9)  

Substituting (7)-(9) into (6), we obtain:

$\frac{dF}{dR}=-\frac{k{Q}^2}{8\pi {\epsilon }_0{R}^3}-20\pi pR-\frac{4\sigma Qa(9R^{2}a+10R{a}^2+3a^3)}{{\epsilon }_0{(2R+a)}^2{(R+a)}^{2}R}.$   (10)  

As we can see, all the terms of this sum are negative, therefore dF/dR < 0. It follows that the system described by equation (5) is in a state of stable equilibrium for any values ​​of k, Q, a and R.

Estimation of the stability time of ball lightning

It is known that ball lightning continuously loses energy in the form of optical and radio frequency radiation. Most likely, the reservoir for storing this radiation is the kinetic energy of protons E_k, which is converted into radiation energy by some mechanism similar to the action of a dynamo. As follows from formula (1), a decrease in E_k leads to a decrease in the force F_cf stretching the shell. This can lead to a change in the equilibrium value of the ball lightning diameter. However, as observations show, the size of ball lightning often remains constant throughout its life.^5. The size of ball lightning will not change if it loses charge simultaneously with energy. Let us estimate at what ratio of the rate of energy loss dE_k/dt and the rate of charge loss dQ/dt it is possible to maintain the radius R and the thickness of the shell a unchanged. From formula (5) we find that the rate of change of the force F_st, stretching the shell, is equal to

$\frac{d{F}_{st}}{dt}=\frac{2}{R}\frac{d{E}_k}{dt}+\frac{2kQ}{8\pi {\epsilon }_0{R}^2}\frac{dQ}{dt},$                     (11)

and the rate of change of the force compressing the shell (at p = const),

$\frac{d{F}_{sh}}{dt}=\frac{4\sigma a}{{\epsilon }_0(2R+a)}\frac{dQ}{dt}.$              (12)

Equating dF_st /dt to dF_sh /dt, we obtain

$\frac{d{E}_k}{dt}=\left[\frac{2\sigma aR}{{\epsilon }_0(2R+a)}-\frac{kQ}{8\pi {\epsilon }_{0}R}\right]\frac{dQ}{dt}.$     (13)

Since the derivative dE_k /dt is equal to P_em – the radiation power of ball lightning, and dQ/dt is the current I flowing from its shell, formula (13) can be rewritten as:

$P_{em}=\left[\frac{2\sigma aR}{{\epsilon }_0(2R+a)}-\frac{kQ}{8\pi {\epsilon }_{0}R}\right]I.$          (14)

      It is not entirely clear what can maintain the balance between the radiation power of ball lightning P_em and the current I flowing from it into the atmosphere – generally speaking, these are processes of different nature. The energy of ball lightning is stored in the form of kinetic energy of protons, and the rate of energy loss in the form of radiation is determined by the degree of violation of the uniformity of charge distribution in the orbit.⁶ The rate of charge loss (current) is determined by the conductivity of the vacuum gap between the energy core and the shell, the conductivity of the shell material and the conductivity of the atmospheric air. However, if we assume that the limiting process is the conductivity of the vacuum gap, then the cause of both processes can be reduced to a violation of the orderliness of the system. This violation, on the one hand, should lead to an increase in the radiation power, and on the other hand, cause the appearance of fast protons capable of overcoming the energy barrier between the core and the shell. Let us consider another case, when the limiting stage of the charge loss process is the conductivity of air. The conductivity of air is determined by the presence of positive and negative ions in it, which appear due to the radioactivity of the soil, cosmic and ultraviolet radiation. The conductivity of air near the earth's surface is λ_a = 3.5·10^-14 (Ohm·m)^-1.⁷ The current density on the surface of the shell of ball lightning is j = Eλ_a, and the electric field strength on the surface of a sphere of radius R in the presence of a charge Q inside it is E = Q/4πε₀R². The total current flowing from the shell into the atmosphere is

$I_a=j·4\pi R^2=\frac{{\lambda }_{a}Q}{{\epsilon }_0}.$    (15)

In this case, the rate of change of the force F_st , compressing the shell, is

$\frac{d{F}_{st}}{dt}=\frac{2}{R}{P}_{em}+\frac{k{\lambda }_a}{4\pi {\epsilon }_0^2{R}^2}{Q}^2\equiv A{P}_{em}+B{Q}^2,$  (16)

and the rate of change of the force, stretching the shell,

$\frac{d{F}_{sh}}{dt}=\frac{4\sigma a}{{\epsilon }_0(2R+a)}\frac{{\lambda }_a}{{\epsilon }_0}Q=\frac{4\sigma a{\lambda }_a}{{\epsilon }_0^2(2R+a)}Q\equiv CQ.$    (17)

As we can see, dF_st /dt ~ Q², and dF_sh /dt ~ Q. Therefore, it can be expected that at small values ​​of the charge Q, when the equilibrium is disturbed, the system will tend to “collapse” (dF_sh /dt > dF_st /dt), and at large Q – to “explode” (dF_sh /dt < dF_st /dt). Figure 1 shows the explosion of ball lightning when it collides with a car.⁸ It can be seen how a sheaf of glowing sparks flies out of it, which are probably the dynamic electric capacitors. The same explosion can occur as a result of other causes of damage to the integrity of the shell.

Figure 1 Collision of ball lightning with a car (filmed by a car DVR). a) The car is approaching ball lightning. b) The moment of collision. c) Scattering of fragments of ball lightning. (http://rutube.ru/tracks/678746.htmail).

Figure 2 shows frames from a video film where the ball lightning emitted a bright flash of light before dying.⁹ Due to the loss of energy for this radiation, the pressure of the core on the shell decreased, the ball lightning lost stability and went out after 0.5 seconds.

Figure 2 A flash of ball lightning. The frame sequence is left-to-right and top-to-bottom. The time between adjacent frames is 1/30 s. The large size of the flash image is due to overexposure of the image. Ball lightning itself retains its shape and size during a flash.

According to formula (15), the current I_a, flowing down from the shell, is

$I_a=\frac{dQ}{dt}=\frac{{\lambda }_a}{{\epsilon }_0}Q.$                                             

From this we find

$Q=Q_0\exp \left(-\frac{{\lambda }_a}{{\epsilon }_0}t\right).$  (18)

The characteristic time of charge decrease by a factor of e is τ_l = ε₀ /λ_a = 253 s. Thus, during the average lifetime of ~ 25 seconds, ball lightning will lose only 10% of its charge. The current flowing into the atmosphere from the lightning shell, which carries a charge of Q = 0.5·10^-2 C, is equal to I = (λ_a /ε₀)·Q = 20 μA. Note that the values ​​of the characteristic time of charge decrease τ_l and current I found by us were obtained for the case when the resistance to current in the vacuum gap between the core and the shell is less than the resistance of atmospheric air. If the resistance of the vacuum gap is limiting, the characteristic time τ_l (and, consequently, the lifetime of ball lightning) will be greater than the value we found, and the current flowing into the atmosphere will be less than I.

Balance of forces in ball lightning

Equation (5), describing the balance of forces acting on the shell of ball lightning, for a given value of the internal radius R, allows us to establish a relationship between the energy E_k, the charge Q and the shell thickness a. Figure 3 shows graphs of the shell thickness a versus the charge Q of the energy core, constructed using formula (5), for R = 3 cm and k = 2 for proton kinetic energy values ​​E_k from 1 to 10⁷ J.

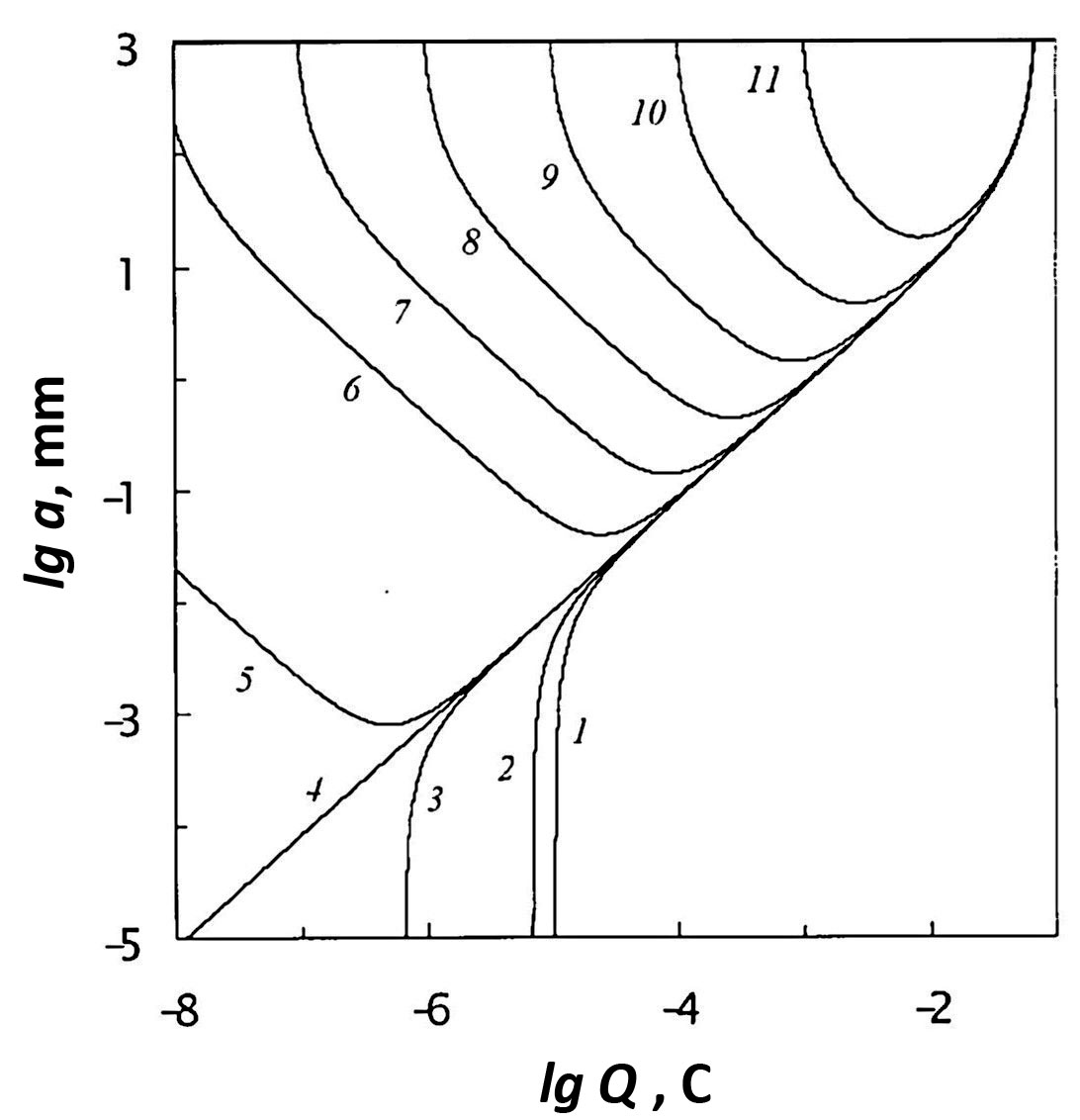
Figure 3 Dependence of the shell thickness a, of ball lightning with an internal shell radius R = 3 cm on the charge Q of the energy core for proton kinetic energy values ​​E_k equal to 1 J (curve 1), 10 J (2), 16.9 J (3), 16.9646 J (4), 17 J (5), 10² J (6), 10³ J (7), 10⁴ J (8), 10⁵ J (9), 10⁶ J (10) and 10⁷ J (11).

It is evident that for values ​​of E_k from 1 to E_k,cr = 16.9646 J with an increase in the value of charge Q, the equilibrium of the system under consideration is maintained with a monotonic increase in the shell thickness a. However, for E_k > E_k,cr, the shape of the curves changes fundamentally: for certain values ​​of charge Q, the value of the shell thickness a turns out to be minimal. For E_k > E_k,cr, under the condition da/dQ = 0, from formula (5) we can find the value of the minimum shell thickness a_m and the corresponding value of charge Q_m:

$Q_m={\left[\frac{16\pi {\epsilon }_{0}R}{k}\left(E_k-2\pi p{R}^3\right)\right]}^{1/2},$  (19)

$a_m=\frac{2R\varphi }{1-\varphi },$            (20)

Where

Equation (5) is square with respect to the charge Q and for a > a_m  it has two roots:

$Q_1=\frac{8\pi R}{k}\left\{\frac{2\sigma aR}{2R+a}+{\left[{\left(\frac{2\sigma aR}{2R+a}\right)}^2-\frac{k{\epsilon }_0(E_k-2\pi p{R}^3)}{4\pi R}\right]}^{1/2}\right\},$             (21)

$Q_2=\frac{8\pi R}{k}\left\{\frac{2\sigma aR}{2R+a}-{\left[{\left(\frac{2\sigma aR}{2R+a}\right)}^2-\frac{k{\epsilon }_0(E_k-2\pi p{R}^3)}{4\pi R}\right]}^{1/2}\right\}.$                 (22)

The first root is approximately equal to

$Q_1=2\frac{8\pi R}{k}\frac{2\sigma aR}{2R+a},$                                

and at k = 2, R = 3·10^-2 m, σ = 1 C/m², a →∞ the charge Q₁ →16πσR² = 4.52·10^-2 C. As can be seen in Figure 3, it is to this charge value that all the curves of the dependence a = f (R) tend for any values ​​of the energy E_k. The second branch of the curve of the dependence a = f (R) represents the values ​​of Q₂ to which the system tends as a →∞. It can be seen that the difference between the limiting values ​​of Q₁ and Q₂ increases with decreasing energy E_k: if for E_k = 10⁷ J it is about 10², then at E_k = 10² J it increases to 10⁷.

Now let us analyze how the energy E_k depends on the inner radius of the shell R. From equation (5) we find

$E_k=2\pi p{R}^3+\frac{2\sigma aRQ}{{\epsilon }_0(2R+a)}-\frac{k{Q}^2}{16\pi {\epsilon }_{0}R}.$           (23)

Substituting Q_m into this expression (see formula (19)), we obtain

${(E_k-2\pi p{R}^3)}^2{\left[\frac{{\epsilon }_0(2R+a)}{\sigma aR}\right]}^2=\frac{16\pi {\epsilon }_{0}R}{k}(E_k-2\pi p{R}^3).$                  (24)

The obvious solution to this equation is (E_k)₁ = 2πpR³. For this value of E_k, as follows from (19), Q_m = 0, and the dependence a(Q) (see Fig. 3) is presented by a curve without a minimum. Physically, this means that the shell exists only due to the equality of the pressure force of the energy core on its inner surface to the force of atmospheric pressure p = 10⁵ Pa acting on the outer surface of the shell. Substituting E_k = 2πpR³ into equation (5), we find

$Q_1=\frac{32\pi \sigma a{R}^3}{k(2R+a)}.$            (25)

For a << R, the charge Q₁ = 16πσaR/k, i.e. equilibrium is possible for any arbitrarily small values ​​of the shell thickness a and the charge Q. For a >> R, the charge Q₁ = 32πσR²/k, i.e. it is equal to its limiting value Q₁, to which all the curves shown in Figure 3 tend. The second solution to equation (24) is

${(E_k)}_2=2\pi p{R}^3+\frac{16\pi {\sigma }^2{a}^2{R}^3}{k{\epsilon }_0{(2R+a)}^2}$       (26)

Let's see how the ratio η = (E_k)₂/(E_k)₁ behaves when the radius R changes:

$\eta =1+\frac{8{\sigma }^2{a}^2}{k{\epsilon }_0{(2R+a)}^{2}p}.$                (27)

At R → 0 η → 1 + 8σ²/kε₀p. Substituting into this expression the values ​​σ = 1 C/m², k = 2 and p = 10⁵ Pa, we find η = 4.52·10⁶, i.e. the energy of the core (E_k)₂, supported by gradient electric forces, exceeds the energy (E_k)₁, supported by atmospheric pressure, by more than 6 orders of magnitude. On the contrary, at R → ∞ η→1. This means that in a large ball lightning the contribution to the energy of the core of gradient forces and atmospheric pressure forces is approximately the same.

“Thrifty” ball lightning

As can be seen from formula (26), the energy (E_k)₂ of small ball lightning increases as the square of the shell thickness a. Since the formation of ball lightning in nature occurs almost instantly,² it will be quite a difficult task for it to collect a sufficient amount of material (water) to create a shell. In this regard, it is interesting to analyze what ball lightning can be like, for which the shell volume V_en is minimal for a given energy value (E_k)₂. For small values ​​of R and large values ​​of (E_k)₂, the term 2πpR³ can be neglected in formula (26). Thus, for k = 2 we have:

${(E_k)}_2\equiv E_k=\frac{8\pi {\sigma }^2{a}^2{R}^3}{{\epsilon }_0(2R+a)}.$      (28)

Solving this equation for a, we find

$a=\frac{2R\xi }{R^{3/2}-\xi }.$       (29)

Here ξ = (E_kε₀/8πσ²)^1/2. The volume of the shell is V_en = (4π/3)[(R + a)³ – R³]. Substituting expression (29) into this formula, we find

$V_{en}=\frac{4\pi }{3}\left[{\left(R+\frac{2R\xi }{R^{3/2}-\xi }\right)}^3-R^3\right].$ (30)       

From the condition dV_en/dR = 0, we can find the value of the internal radius of the shell R_m,_v, at which its volume is minimal: R_m,v = 2.57ξ^2/3. In the low of depending of the external radius of the shell R+a from the value of the internal radius R,

$R+a=R+\frac{2R\xi }{R^{3/2}-\xi },$                               (31)

a minimum is also observed at R_m = [ξ (3+√13)/2]^2/3 = 2.218 ξ^2/3. The value of R_m,_v is 1.159 times greater than R_m. From formulas (29) – (31) we find that at energy E_k = 10⁸ J R_m = 7.27 cm and R_m,_v = 8.43 cm, and at E_k = 10⁹ J R_m = 15.67 cm and R_m,v =18.15 cm. In this case, for E_k = 10⁹ J the shell thickness a = 11.64 cm, its outer radius R + a is equal to 29.79 cm, and the shell volume V_en = 85.65 l.

Figure 4 shows how the outer radius of ball lightning R + a, the volume of the shell V_en and the charge of the energy core Q (see formula (19)) depend on the energy E_k in the case when the volume of the shell is minimal. The dots mark the values ​​of the energy and radius of ball lightning found on the basis of observations. In general, good agreement can be noted between the calculated and measured values ​​of energy and size, with the exception of one case. Thus, the diameter of ball lightning with an energy of 260 MJ, which evaporated water in a trough,¹¹ was equal to 6.5 cm, whereas our model predicts a value of 2(R + a) = 35 cm for such energy. One of the reasons for this discrepancy may be that in our estimates we took the energy of ball lightning to be equal to the kinetic energy of protons, ignoring the additional energy in the form of the energy of electrons, as well as the energy of electric and magnetic fields.

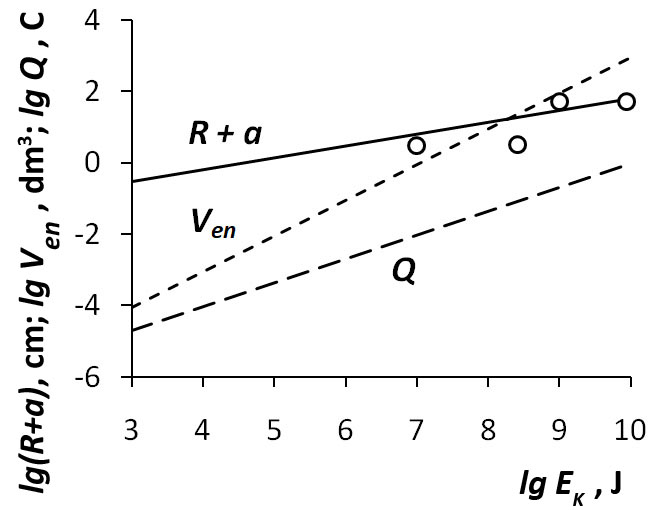
Figure 4 Dependence of the outer radius of ball lightning R + a, the volume of the shell V_en and the charge of the energetic core Q on the kinetic energy of protons E_k for the case of the minimum value of the shell volume. The circles mark the values ​​of the outer radius of observed ball lightning with known energy values ​​(from left to right): 10 MJ;¹⁰ 260 MJ;¹¹ 1000 MJ;122300 MJ.¹³

Above we considered the possibility of accumulation of large amounts of energy in medium-sized ball lightning. However, no less interesting is the question of what ball lightning with a “modest” energy of 100 – 1000 J can be. The conducted analysis gives grounds to believe that if some energy barrier to the formation of ball lightning exists, it should be quite low. In this regard, we will estimate the size of “compact” ball lightning with an internal energy of 100 and 1000 J. Substituting E_k = 100 J into formula (29), we find ξ = 0.5937·10^-5 m^3/2 and the shell thickness a = 5.4·10^-4 m. The inner radius R_m,_v = 8.426·10^-4 m, and the outer radius R_m,_v + a = 1.38 mm. For energy E_k = 1000 J  ξ = 1.8774·10^-5 m^3/2, a = 11.637·10^-4 m, R_m,_v = 18.154·10^-4 m and R_m,_v+ a = 2.98 mm. Thus, the existence of miniature ball lightning with dimensions of several millimeters in nature is quite probable. This makes us take seriously Matsumoto's experiments on studying electrical discharges in water, in which he discovered traces of objects that he called microscopic ball lightning.^14,15 As can be seen in Figure 3, for a given energy value, the existence of not only ball lightning with minimal values ​​of radius and shell thickness, but also objects of larger dimensions is possible. Therefore, the estimates we have obtained should be treated as a definition of the lower limit of the size of ball lightning, without denying the existence of low-energy lightning with dimensions of several centimeters.

We found that in ball lightning with a large energy reserve, the volume of the shell can be several tens of liters and, therefore, its mass (if the density of the shell substance is close to the density of water) can be equal to tens of kilograms. Therefore, the question arises whether such a heavy ball lightning is capable of hovering in the air: after all, for a mass of 85 kg, the lifting force must be about F_g = 850 N. The Archimedes force acting on ball lightning with a radius of 20 cm cannot compensate for the force of gravity. The reason for the creation of lifting force can be the effect of the atmospheric electric field on the charge of ball lightning. If, for example, the charge is Q = 10^-2 C, then to create a lifting force of 850 N, it is necessary that the electric field strength be no less than E = F_g /Q = 8.5·10⁴ V/m. Electric fields of this magnitude are observed during rainy weather.

For ball lightning with a diameter of several meters, the severity of the problem of creating a lifting force is reduced due to the presence of a fairly noticeable Archimedes force F_ar = (4/3)π(R+a)³ρ_airg, where g is the acceleration of gravity, and ρ_air is the air density. Near the surface of the earth, ρ_air = 1.293 kg/m³, therefore, for ball lightning with R + a = 5 m, F_ar = 6638 N. This force is capable of holding a ball lightning with a mass of 677 kg in the air. Considering that the main part of the mass of ball lightning is concentrated in its shell, the density of the substance of which is equal to the density of water ρ_w, we can find the thickness of the shell a = (R+a)ρ_air/3ρ_w= 2.15 mm. There are reports of observations from aircraft of spherical objects up to 100 m in diameter flying at an altitude of about 10,000 m.^16,17 If we assume that these objects are large ball lightning, we can estimate the parameters of their shells. Let the radius of the object be 50 m. The air density at an altitude of 10 km is ρ_air,_h = 0.4127 kg/m³. Substituting the data into the formulas above, we find F_ar = 2.119·10⁶ N, the mass of the object is 216 t and the thickness of the shell a = 6.88 mm.

In the approach to solving the problem of ball lightning, an object of electrical nature, it seems natural to assume that it consists of electric charges of opposite signs, held by their own forces. The force of mutual attraction of opposite charges can be compensated by the centrifugal force of their rotation. Many models of ball lightning constructed according to this scheme have been proposed (see, for example,^18-20), and experiments were conducted to create plasmoids in electric discharges.²¹ However, these plasmoids existed only for a very short time. Shafranov²² proved that the creation of a system of moving charges that is held by its own forces is impossible. Our contributions to solving this problem were: 1) the assumption that the plasmoid has an uncompensated electric charge and 2) the addition of a container of polarized water molecules to the system of unstable plasmoids.^23-25 We have shown that such a system has a large reserve of energy and is stable. Moreover, this system maintains stability for some time when the rate of its energy loss to radiation is consistent with the rate of charge loss. When the balance of speeds is disturbed, an explosion or collapse of ball lightning occurs. The assumption that the system contains electrons, moving at high speed in closed orbits, allows us to explain the details of the nature of ball lightning radiation in the optical and radio frequency ranges of the spectrum.

1. Nikitin AI. Electrodynamic model of ball lightning. Phys Astron Int J. 2024;8(3):150–154.
2. Nikitin AI. Birthplace of ball lightning. Phys Astron Int J. 2024;8(1):38–46.
3. Sarancev VP, Perel’shtein EA. Collective acceleration of ions by electron rings. Mosow: Atomizdat. 1979.
4. Zel’dovich YaB, Yaglom IM. Higher mathematics for beginning physicists and techniciants. Moscow: Nauka. 1982.
5. Stenhoff M. Ball lightning. An unsolved problem in atmospheric physics. London: Kluwer Acad. 1999.
6. Nikitin AI, Nikitin VA, Velichko AM, et al. Features of the mechanism of ball lightning electromagnetic radiation. J Atm Solar–Terr Phys. 2021;222:105711.
7. Chalmers JA. Atmospheric electricity. Oxford: Clarendon Press, 1949.
8. Nikitin AI, Nikitin VA, Velichko AM, et al. Explosions of ball lightning inside enclosed spaces. Atmosphere. 2024;15:2.
9. Nikitin AI. The danger of ball lightning. Phys Astron Int J. 2023;7(2):91–97.
10. Goodlet BL. Lightning. J Inst Elect Eng. 1937;81:1.
11. Imianitov I, Tikhiy D. Beyond a boundary of laws of a science. Moscow: Atomizdat. 1980.
12. Dmitriev MT, Bakhtin BI, Martynov VI. The theremal factor of ball lightning. Zh Tekh Fiz. 1981;51(12):2567–2572.
13. Batygin A, Mosin I. Visit of the fire lady. The newspaper “Pravda”. 1989; 220:8.
14. Matsumoto T. Ball lightning during underwater spark discharges and the Matsumae earth–quarks. Proc. 5th Intern. Symp. on Ball Lightning (ISBL–97). Tsugawa–Town,  Niigata, Japan, 1997, 193–201 р.
15. Matsumoto T. Micro ball lightning during underwater spark discharges. Proc. 6th Intern. Symp. on Ball Lightning (ISBL–99). Antwerp, Belgium, 1999, 249–254 р.
16. Vostrukhin V. Exactly at 4.10. The newspaper “Trud”. Moscow: 30 January 1985, p. 3.
17. Chernobrov V. Chronics of the UFO’s visits. Moscow: Drofa. 2003.
18. Koloc PM. Plasmak star power for energy intensive space applications. Fusion Technol. 1989;15:1136–1141.
19. Oreshko AG, Oreshko AA, Mavlyudov TV. Proton–electron model of ball lightning structure. J Atm Solar–Terr Phys. 2019;182:194–199.
20. Shchedrin AI. Relativistic model of ball lightning. Moscow: Goryachaya Liniya–Telekom. 2018
21. Bostik WH. Experimental study of ionized matter projected across a magnetic field. Phys Rev. 1956;104(2):292–299.
22. Shafranov VD. On magnetohydrodynamical equilibrium configurations. Sov Phys JETP. 1957;6:545–547.
23. Nikitin AI. Electrodynamic model of ball lightning. Khimicheskaya Fizika. 2006;25(3):38–62.
24. Nikitin AI.  Possible process of ball lightning training in nature. J Atm Solar–Terr Phys. 2019;190:54–61.
25. Nikitin AI.  My ball lightning. Moscow: Nauka. 2022.